4edo
| ← 3edo | 4edo | 5edo → |
4 equal divisions of the octave (abbreviated 4edo or 4ed2), also called 4-tone equal temperament (4tet) or 4 equal temperament (4et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 4 equal parts of exactly 300 ¢ each. Each step represents a frequency ratio of 21/4, or the 4th root of 2.
Theory
Like 3edo, 4edo is already familiar as a chord of 12edo. Not only that, but 4edo establishes tonality in much the same ways that 3edo does—with only two notes at a time as opposed to three aside from octave reduplications of the tonic, though the Tonic-Antitonic contrast from 2edo also works. Also like with 3edo, it has a theoretical interest in that it preserves a kind of outline, or skeleton, of melodic movement while erasing key distinctions concerning harmony. The 7-limit mapping, or val, for 4edo goes ⟨4 6 9 11], all of which are distinct modulo 4. It therefore goes with tetradic harmony in much the same way that 3edo goes with triadic harmony, mapping the 7-limit consistently, and sending 15/14, 21/20, 25/24, and 36/35 to the unison. Somewhat confusingly, the patent mapping of 4edo sees 9/8 mapped to the unison also, leading to antitonic, though this can be traced to both 3/2 and 4/3 being mapped to 2\4.
By putting together the triples of integers which uniquely represent 7-limit tetrads in the 7-limit cubic lattice of tetrads with the number of 4edo steps returned by the ⟨4 6 9 11] we obtain a representation of the 7-limit in terms of four integers, which differs from the usual (monzo) representation in that the triple representing the chord can be swapped for another such triple, resulting in a similar note tuned to a different chord. It is even possible under some circumstances to create a sort of recombinant merging of two pieces of music by using the chords of one with the 4edo skeletons of another.
We can also add more kinds of chords, for instance the subminor (1–7/6–3/2–5/3) and supermajor (1–9/7–3/2–9/5) to the mix, and by encoding which kind of tetrad a note reconstitute a version of 9-odd-limit tetradic harmony, again changing the harmonic content of a note without changing its 4edo skeletal position.
4edo can ne viewed as a dual-fifth system (the smallest in fact), with the tritone and major sixth as the flat and sharp "fifths". The tritone is the the patent val while the major sixth is in 4b-edo (using wart notation). 4b-edo has one of the sharpest mappings of 3/2 of any octave-repeating equal temperaments, only outmatched by that of 1edo, and even falling outside of the 600- to 800-cent range of 2L 1s.
4edo can be seen as a trivial tuning of the diminished temperament, since it tempers out 648/625 (the major diesis) by equating four minor thirds (6/5) to an octave. Alternately, it can be viewed as a critically flat hanson or myna tuning, as both 6 and 10 generators reach the best approximation to the 5th. This interpretation works best if you stretch the octaves, 4edo is the first edo that is zeta peak but not zeta peak integer, which means the point of maximum harmonicity is somewhat further away from pure octaves than the previous two edos. If you compress the octaves instead, it can be interpreted as a critically sharp gariberttet tuning.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -102 | -86 | -69 | +96 | +49 | +59 | +112 | -105 | +2 | +129 | -28 |
| Relative (%) | -34.0 | -28.8 | -22.9 | +32.0 | +16.2 | +19.8 | +37.2 | -35.0 | +0.8 | +43.1 | -9.4 | |
| Steps (reduced) |
6 (2) |
9 (1) |
11 (3) |
13 (1) |
14 (2) |
15 (3) |
16 (0) |
16 (0) |
17 (1) |
18 (2) |
18 (2) | |
Subsets and supersets
4edo is the first composite edo, containing 2edo as the only nontrivial subset edo.
Intervals
| Degree | Cents | Interval region | Approximated JI intervals* (error in ¢) | Audio | |||
|---|---|---|---|---|---|---|---|
| 3-limit | 5-limit | 7-limit | Other | ||||
| 0 | 0 | Unison (prime) | 1/1 (just) | ||||
| 1 | 300 | Minor third | 32/27 (+5.865) | 6/5 (-15.641) | 7/6 (+33.129) 25/21 (-1.847) |
19/16 (+2.487) | |
| 2 | 600 | Tritone | 7/5 (+17.488) 10/7 (-17.488) |
24/17 (+3.000) 99/70 (-0.088) 17/12 (-3.000) |
|||
| 3 | 900 | Major sixth | 27/16 (-5.865) | 5/3 (+15.641) | 42/25 (+1.847) 12/7 (-33.129) |
32/19 (-2.487) | |
| 4 | 1200 | Octave | 2/1 (just) | ||||
* Based on treating 4edo as a subset of 12edo, itself treated as a 2.3.5.7.17.19 subgroup temperament; other approaches are possible.
Notation
| Degree | Cents | 12edo subset notation | |
|---|---|---|---|
| Diatonic interval names | Note names (on D) | ||
| 0 | 0 | Perfect unison (P1) | D |
| 1 | 300 | Augmented second (A2) Minor third (m3) |
E# F |
| 2 | 600 | Augmented fourth (A4) Diminished fifth (d5) |
G# Ab |
| 3 | 900 | Major sixth (M6) Diminished seventh (d7) |
B Cb |
| 4 | 1200 | Perfect octave (P8) | D |
In 4edo:
- ups and downs notation is identical to standard notation;
- Mixed sagittal notation is identical to standard notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp (
 ) and sagittal flat (
) and sagittal flat (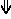 ) respectively.
) respectively.
Solfege
| Degree | Cents | 12edo subset standard solfege (movable do) |
12edo subset Uniform solfege (2-3 vowels) |
|---|---|---|---|
| 0 | 0 | Do (P1) | Da (P1) |
| 1 | 300 | Ri (A2) Me (m3) |
Ru (A2) Na (m3) |
| 2 | 600 | Fi (A4) Se (d5) |
Pa (A4) Sha (d5) |
| 3 | 900 | La (M6) | La (M6) Tho (d7) |
| 4 | 1200 | Do (P8) | Da (P8) |
Music
- "Mimetism", from Tribute to Armodue (2008)
- Dimpulse (2024)
- "Entering", from Edolian (2020)
- Diminished (2024)
- Nothing of any importance (2006) – his contribution to the MMM day 2006[where?]
- A simple 4EDO piece (2011?) – see also Composing with tablets
- "Neainaz Antithetica, Variation II", from STAFFcirc vol. 7 (2021) – SoundCloud | Bandcamp