13edt
(Redirected from 13ed3)
Jump to navigation
Jump to search
| ← 12edt | 13edt | 14edt → |
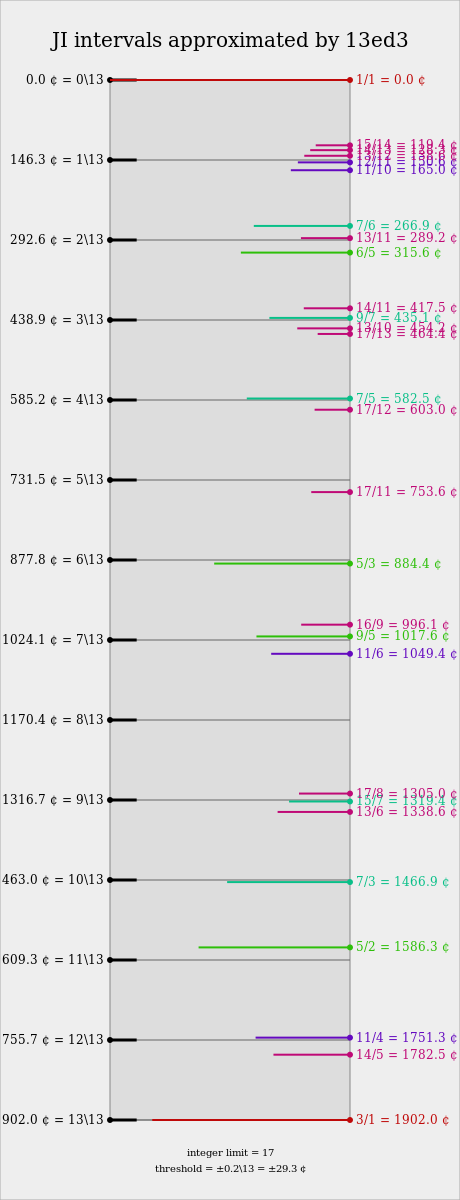
13 equal divisions of the tritave (13edt) is the nonoctave tuning system derived by dividing the tritave (3/1) into 13 equal steps of 146.3 cents each, or the thirteenth root of 3. It is best known as the equal-tempered version of the Bohlen-Pierce scale.
13edt can be described as approximately 8.202edo. This implies that each step of 13edt can be approximated by 5 steps of 41edo.
In the 7-limit, it tempers out 245/243 and 3125/3087, the same commas as bohpier temperament. It is less impressive in higher prime limits, but makes for excellent no-twos 7-limit harmony. For higher limits, the multiples of 13 (26edt, 39edt and 52edt) come to the fore.
Theory
| Prime interval | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | |
|---|---|---|---|---|---|---|---|---|---|
| Error | absolute (¢) | -29.6 | 0.0 | -6.5 | -3.8 | -54.8 | -51.4 | +69.4 | +23.1 |
| relative (%) | -20 | 0 | -4 | -3 | -37 | -35 | +47 | +16 | |
| Patent val | 8 | 13 | 19 | 23 | 28 | 30 | 34 | 35 | |
| Fifthspan | -1 | 0 | -4 | +2 | +3 | +6 | -1 | -6 | |
Intervals
- Main article: Intervals of BP
| Steps | Cents | Hekts | BP nonatonic degree | Corresponding JI intervals | Comments | Generator for... | Arcturus nonatonic notation (J = 1/1) |
|---|---|---|---|---|---|---|---|
| 1 | 146.3 | 100 | A1/m2 | 27/25~49/45 | J# | ||
| 2 | 292.6 | 200 | M2/d3 | 25/21 | Sirius | Kb | |
| 3 | 438.9 | 300 | A2/P3/d4 | 9/7 | Linear BP | K | |
| 4 | 585.2 | 400 | A3/m4/d5 | 7/5 | Canopus | K#, Lb | |
| 5 | 731.5 | 500 | M4/m5 | 75/49 | false 3/2 | false Father | L |
| 6 | 877.8 | 600 | A4/M5 | 5/3 | Arcturus | M | |
| 7 | 1024.1 | 700 | A5/m6/d7 | 9/5 | Arcturus | N | |
| 8 | 1170.4 | 800 | M6/m7 | 49/25 | false 2/1 | false Father | N#, Ob |
| 9 | 1316.7 | 900 | A6/M7/d8 | 15/7 | Canopus | O | |
| 10 | 1463.0 | 1000 | P8/d9 | 7/3 | Linear BP | P | |
| 11 | 1609.3 | 1100 | A8/m9 | 63/25 | Sirius | Q | |
| 12 | 1755.7 | 1200 | M9/d10 | 25/9~135/49 | R | ||
| 13 | 1902.0 | 1300 | A9/P10 | 3/1 | Tritave | J |
JI approximation
Regular temperament properties
- Main article: Bohlen-Pierce #Regular temperament properties
See also
- Bohlen-p_et
- Catalog of 3.5.7 subgroup rank two temperaments
- 19ED5: relative ED5
- 23ED7: relative ED7