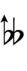62edo: Difference between revisions

62 = 2 × 31 and the patent val of 62edo is a contorted 31edo through the 11-limit, but it makes for a good tuning in the higher limits. In the 13-limit it tempers out 169/168, 1188/1183, 847/845 and 676/675; in the 17-limit 221/220, 273/272, and 289/288; in the 19-limit 153/152, 171/170, 209/208, 286/285, and 361/360. Unlike 31edo, which has a sharp profile for primes 13, 17, 19 and 23, 62edo has a flat profile for these, as it removes the distinction of otonal and utonal superparticular pairs of the primes (e.g. 13/12 vs 14/13 for prime 13) by tempering out the corresponding square-particulars. Interestingly, the relative size differences of consecutive harmonics are well preserved for all first 24 harmonics, and 62edo is one of the few meantone edos that achieve this, great for those who seek higher-limit meantone harmony.

It provides the optimal patent val for gallium, semivalentine and hemimeantone temperaments.

Using the 35\62 generator, which leads to the ⟨62 97 143 173] val, 62edo is also an excellent tuning for septimal mavila temperament; alternatively ⟨62 97 143 172] supports hornbostel.

Odd harmonics

Approximation of odd harmonics in 62edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	-5.18	+0.78	-1.08	+8.99	-9.38	-8.27	-4.40	-8.18	-7.19	-6.26	-8.92
Error	Relative (%)	-26.8	+4.0	-5.6	+46.5	-48.5	-42.7	-22.7	-42.3	-37.2	-32.4	-46.1
Steps (reduced)		98 (36)	144 (20)	174 (50)	197 (11)	214 (28)	229 (43)	242 (56)	253 (5)	263 (15)	272 (24)	280 (32)

Subsets and supersets

Since 62 factors into 2 × 31, 62edo does not contain nontrivial subset edos other than 2edo and 31edo. 186edo and 248edo are notable supersets.

Miscellaneous properties

62 years is the amount of years in a leap week calendar cycle which corresponds to a year of 365 days 5 hours 48 minutes 23 seconds, meaning it is both a simple cycle for a calendar, and 62 being a multiple of 31 makes it a harmonically useful and playable cycle. The corresponding maximal evenness scales are 15 & 62 and 11 & 62.

The 11 & 62 temperament in the 2.9.7 subgroup tempers out 44957696/43046721, and the three generators of 17\62 correspond to 16/9. It is possible to extend this to the 11-limit with comma basis {896/891, 1331/1296}, where 17\62 is mapped to 11/9 and two of them make 16/11. In addition, three generators make the patent val 9/8, which is also created by combining the flat patent val fifth from 31edo with the sharp 37\62 fifth.

The 15 & 62 temperament, corresponding to the leap day cycle, is an unnamed extension to valentine in the 13-limit.

Intervals

Steps	Cents	Approximate ratios*	Ups and downs notation
0	0.00	1/1	D
1	19.35	65/64, 66/65, 78/77, 91/90, 105/104	^D, vE♭♭
2	38.71	33/32, 36/35, 45/44, 49/48, 50/49, 55/54, 56/55, 64/63	^^D, E♭♭
3	58.06	26/25, 27/26	vD♯, ^E♭♭
4	77.42	21/20, 22/21, 23/22, 24/23, 25/24, 28/27	D♯, vvE♭
5	96.77	17/16, 18/17, 19/18, 20/19	^D♯, vE♭
6	116.13	15/14, 16/15	^^D♯, E♭
7	135.48	13/12, 14/13	vD𝄪, ^E♭
8	154.84	11/10, 12/11, 23/21	D𝄪, vvE
9	174.19	21/19	^D𝄪, vE
10	193.55	9/8, 10/9, 19/17, 28/25	E
11	212.90	17/15	^E, vF♭
12	232.26	8/7	^^E, F♭
13	251.61	15/13, 22/19	vE♯, ^F♭
14	270.97	7/6	E♯, vvF
15	290.32	13/11, 19/16, 20/17	^E♯, vF
16	309.68	6/5	F
17	329.03	17/14, 23/19	^^F, G♭♭
18	348.39	11/9, 27/22, 28/23	^^F, G♭♭
19	367.74	16/13, 21/17, 26/21	vF♯, ^G♭♭
20	387.10	5/4	F♯, vvG♭
21	406.45	19/15, 24/19	^F♯, vG♭
22	425.81	9/7, 14/11, 23/18, 32/25	^^F♯, G♭
23	445.16	13/10, 22/17	vF𝄪, ^G♭
24	464.52	17/13, 21/16, 30/23	F𝄪, vvG
25	483.87	25/19	^F𝄪, vG
26	503.23	4/3	G
27	522.58	19/14, 23/17	^G, vA♭♭
28	541.94	11/8, 15/11, 26/19	^^G, A♭♭
29	561.29	18/13	vG♯, ^A♭♭
30	580.65	7/5, 25/18, 32/23	G♯, vvA♭
31	600.00	17/12, 24/17	E
32	619.35	10/7, 23/16, 36/25	^^G♯, A♭
33	638.71	13/9	vG𝄪, ^A♭
34	658.06	16/11, 19/13, 22/15	G𝄪, vvA
35	677.42	28/19, 34/23	^G𝄪, vA
36	696.77	3/2	A
37	716.13	38/25	^A, vB♭♭
38	735.48	23/15, 26/17, 32/21	^^A, B♭♭
39	754.84	17/11, 20/13	vA♯, ^B♭♭
40	774.19	11/7, 14/9, 25/16, 36/23	A♯, vvB♭
41	793.55	19/12, 30/19	^A♯, vB♭
42	812.90	8/5	^^A♯, B♭
43	832.26	13/8, 21/13, 34/21	vA𝄪, ^B♭
44	851.61	18/11, 23/14, 44/27	A𝄪, vvB
45	870.97	28/17, 38/23	^A𝄪, vB
46	890.32	5/3	B
47	909.68	17/10, 22/13, 32/19	^B, vC♭
48	929.03	12/7	^^B, C♭
49	948.39	19/11, 26/15	vB♯, ^C♭
50	967.74	7/4	B♯, vvC
51	987.10	30/17	^B♯, vC
52	1006.45	9/5, 16/9, 25/14, 34/19	C
53	1025.81	38/21	^C, vD♭♭
54	1045.16	11/6, 20/11, 42/23	^^C, D♭♭
55	1064.52	13/7, 24/13	vC♯, ^D♭♭
56	1083.87	15/8, 28/15	C♯, vvD♭
57	1103.23	17/9, 19/10, 32/17, 36/19	^C♯, vD♭
58	1122.58	21/11, 23/12, 27/14, 40/21, 44/23, 48/25	^^C♯, D♭
59	1141.94	25/13, 52/27	vC𝄪, ^D♭
60	1161.29	35/18, 49/25, 55/28, 63/32, 64/33, 88/45, 96/49, 108/55	C𝄪, vvD
61	1180.65	65/33, 77/39, 128/65, 180/91, 208/105	^C𝄪, vD
62	1200.00	2/1	D

* 23-limit patent val, inconsistent intervals in italic

Notation

Ups and downs notation

62edo can be notated with quarter-tone accidentals and ups and downs. This can be done by combining sharps and flats with arrows borrowed from extended Helmholtz-Ellis notation:

Step offset	0	1	2	3	4	5	6	7	8	9
Sharp symbol
Flat symbol

Armodue notation

Armodue nomenclature 8;3 relation

Ɨ = Thick (1/8-tone up)
‡ = Semisharp (1/4-tone up)
b = Flat (5/8-tone down)
◊ = Node (sharp/flat blindspot 1/2-tone)
# = Sharp (5/8-tone up)
v = Semiflat (1/4-tone down)
⌐ = Thin (1/8-tone down)

#		Cents	Armodue notation	Associated ratio
0		0.0	1
1		19.4	1Ɨ
2		38.7	1‡ (9#)
3		58.1	2b
4		77.4	1◊2
5		96.8	1#
6		116.1	2v
7		135.5	2⌐
8		154.8	2	11/10~12/11
9		174.2	2Ɨ
10		193.5	2‡
11		212.9	3b	8/7
12		232.3	2◊3
13		251.6	2#
14		271.0	3v
15		290.3	3⌐
16		309.7	3	6/5~7/6
17		329.0	3Ɨ
18		348.4	3‡
19	·	367.7	4b	5/4
20		387.1	3◊4
21		406.5	3#
22		425.8	4v (5b)
23		445.2	4⌐
24		464.5	4
25		483.9	4Ɨ (5v)
26		503.2	5⌐ (4‡)
27	·	522.6	5	4/3~11/8
28		541.9	5Ɨ
29		561.3	5‡ (4#)
30		580.6	6b	10/7
31		600.0	5◊6
32		619.4	5#	7/5
33		638.7	6v
34		658.1	6⌐
35	·	677.4	6	3/2~16/11
36		696.8	6Ɨ
37		716.1	6‡
38		735.5	7b
39		754.8	6◊7
40		774.2	6#
41		793.5	7v
42		812.9	7⌐
43	·	832.3	7	8/5
44		851.6	7Ɨ
45		871.0	7‡
46		890.3	8b	5/3~12/7
47		909.7	7◊8
48		929.0	7#
49		948.4	8v
50		967.7	8⌐
51		987.1	8	7/4
52		1006.5	8Ɨ
53		1025.8	8‡
54		1045.2	9b	11/6~20/11
55		1064.5	8◊9
56		1083.9	8#
57		1103.2	9v (1b)
58		1122.6	9⌐
59		1141.9	9
60		1161.3	9Ɨ (1v)
61		1180.6	1⌐ (9‡)
62		1200.0	1

Regular temperament properties

62edo is contorted 31edo through the 11-limit. Template:Comma basis begin |- | 2.3.5.7.11.13 | 81/80, 99/98, 121/120, 126/125, 169/168 | [⟨62 98 144 174 214 229]] | +1.38 | 1.41 | 7.28 |- | 2.3.5.7.11.13.17 | 81/80, 99/98, 121/120, 126/125, 169/168, 221/220 | [⟨62 98 144 174 214 229 253]] | +1.47 | 1.32 | 6.83 |- | 2.3.5.7.11.13.17.19 | 81/80, 99/98, 121/120, 126/125, 153/152, 169/168, 209/208 | [⟨62 98 144 174 214 229 253 263]] | +1.50 | 1.24 | 6.40 |- | 2.3.5.7.11.13.17.19.23 | 81/80, 99/98, 121/120, 126/125, 153/152, 161/160, 169/168, 209/208 | [⟨62 98 144 174 214 229 253 263 280]] | +1.55 | 1.18 | 6.09 Template:Comma basis end

Rank-2 temperaments

Template:Rank-2 begin |- | 1 | 3\62 | 58.06 | 27/26 | Hemisecordite |- | 1 | 7\62 | 135.48 | 13/12 | Doublethink |- | 1 | 13\62 | 251.61 | 15/13 | Hemimeantone |- | 1 | 17\62 | 329.03 | 16/11 | Mabon |- | 2 | 3\62 | 58.06 | 27/26 | Semihemisecordite |- | 2 | 4\62 | 77.42 | 21/20 | Semivalentine |- | 2 | 6\62 | 116.13 | 15/14 | Semimiracle |- | 2 | 26\62 | 503.22 | 4/3 | Semimeantone |- | 31 | 29\62
(1\62) | 561.29
(19.35) | 11/8
(196/195) | Kumhar (62e) |- | 31 | 19\62
(1\62) | 367.74
(19.35) | 16/13
(77/76) | Gallium Template:Rank-2 end Template:Orf

@@ Line 3: / Line 3: @@
 == Theory ==
-= 2 × 31 and the [[patent val]] of 62edo is a contorted [[31edo]] through the 11-limit, but it makes for a good tuning in the higher limits. In the 13-limit it tempers out [[169/168]], [[1188/1183]], [[847/845]] and [[676/675]]; in the 17-limit [[221/220]], [[273/272]], and [[289/288]]; in the 19-limit [[153/152]], [[171/170]], [[209/208]], [[286/285]], and [[361/360]]. Unlike 31edo, which has a sharp profile for primes [[13/1|13]], [[17/1|17]], [[19/1|19]] and [[23/1|23]], 62edo has a flat profile for these, as it removes the distinction of otonal and utonal [[superparticular]] pairs of the primes (e.g. 13/12 vs 14/13 for prime 13) by tempering out the corresponding [[square-particular]]s. Interestingly, the relative size differences of consecutive harmonics are well preserved for all first 24 harmonics, and 62edo is one of the few meantone edos that achieve this, great for those who seek higher-limit [[meantone]] harmony.
+{{nowrap|62 {{=}} 2 &times; 31}} and the [[patent val]] of 62edo is a contorted [[31edo]] through the 11-limit, but it makes for a good tuning in the higher limits. In the 13-limit it tempers out [[169/168]], [[1188/1183]], [[847/845]] and [[676/675]]; in the 17-limit [[221/220]], [[273/272]], and [[289/288]]; in the 19-limit [[153/152]], [[171/170]], [[209/208]], [[286/285]], and [[361/360]]. Unlike 31edo, which has a sharp profile for primes [[13/1|13]], [[17/1|17]], [[19/1|19]] and [[23/1|23]], 62edo has a flat profile for these, as it removes the distinction of otonal and utonal [[superparticular]] pairs of the primes (e.g. 13/12 vs 14/13 for prime 13) by tempering out the corresponding [[square-particular]]s. Interestingly, the relative size differences of consecutive harmonics are well preserved for all first 24 harmonics, and 62edo is one of the few meantone edos that achieve this, great for those who seek higher-limit [[meantone]] harmony.
 It provides the [[optimal patent val]] for [[31st-octave temperaments#Gallium|gallium]], [[Starling temperaments #Valentine|semivalentine]] and [[Meantone family #Hemimeantone|hemimeantone]] temperaments.
@@ Line 27: / Line 27: @@
 ! Steps
 ! Cents
-! Approximate Ratios*
+! Approximate ratios*
-! [[Ups and downs notation|Ups and Downs Notation]]
+! [[Ups and downs notation]]
 |-
 | 0
@@ Line 345: / Line 345: @@
 | {{UDnote|step=62}}
 |}
-<nowiki>*</nowiki> 23-limit patent val, inconsistent intervals in ''italic''
+<nowiki />* 23-limit patent val, inconsistent intervals in ''italic''
 == Notation ==
@@ Line 365: / Line 365: @@
 {| class="wikitable center-all right-3 left-5 mw-collapsible mw-collapsed"
 |-
-! colspan="2" | #
+! colspan="2" | &#35;
 ! Cents
-! Armodue Notation
+! Armodue notation
-! Associated Ratio
+! Associated ratio
 |-
 | 0
@@ Line 751: / Line 751: @@
 == Regular temperament properties ==
 edo is contorted 31edo through the 11-limit.
-{| class="wikitable center-4 center-5 center-6"
+{{comma basis begin}}
-! rowspan="2" | [[Subgroup]]
-! rowspan="2" | [[Comma list|Comma List]]
-! rowspan="2" | [[Mapping]]
-! rowspan="2" | Optimal <br>8ve Stretch (¢)
-! colspan="2" | Tuning Error
-|-
-! [[TE error|Absolute]] (¢)
-! [[TE simple badness|Relative]] (%)
 |-
 | 2.3.5.7.11.13
@@ Line 788: / Line 780: @@
 | 1.18
 | 6.09
-|}
+{{comma basis end}}
 === Rank-2 temperaments ===
-{| class="wikitable center-all left-5"
+{{rank-2 begin}}
-! Periods<br>per 8ve
-! Generator*
-! Cents*
-! Associated<br>Ratio*
-! Temperaments
 |-
 | 1
@@ Line 847: / Line 834: @@
 |-
 | 31
-| 29\62<br>(1\62)
+| 29\62<br />(1\62)
-| 561.29<br>(19.35)
+| 561.29<br />(19.35)
-| 11/8<br>(196/195)
+| 11/8<br />(196/195)
 | [[Kumhar]] (62e)
 |-
 | 31
-| 19\62<br>(1\62)
+| 19\62<br />(1\62)
-| 367.74<br>(19.35)
+| 367.74<br />(19.35)
-| 16/13<br>(77/76)
+| 16/13<br />(77/76)
 | [[Gallium]]
-|}
+{{rank-2 end}}
-<nowiki>*</nowiki> [[Normal lists|octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if it is distinct
+{{orf}}

62edo: Difference between revisions

Revision as of 06:34, 16 November 2024

Contents