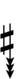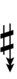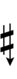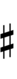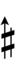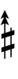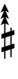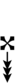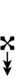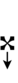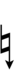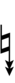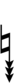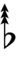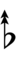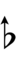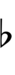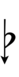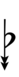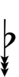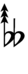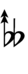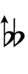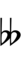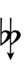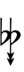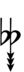77edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
Contribution (talk | contribs)
autopatrolled
2,880 edits
No edit summary
ArrowHead294 (talk | contribs)
14,512 edits
m Formatting + ups and downs notation
Line 5: Line 5:
With [[3/1|harmonic 3]] less than a cent flat, [[5/1|harmonic 5]] a bit over three cents sharp and [[7/1|7]]'s less flat than that, 77edo represents an excellent tuning choice for both [[valentine]], the {{nowrap|31 & 46}} temperament, and [[starling]], the [[126/125]] [[planar temperament]], giving the [[optimal patent val]] for [[11-limit]] valentine and its [[13-limit]] extensions dwynwen and valentino, as well as 11-limit starling and [[oxpecker]] temperaments. It also gives the optimal patent val for [[grackle]] and various members of the [[unicorn family]], with a [[generator]] of 4\77 instead of the 5\77 (which gives valentine). These are 7-limit [[Unicorn family #Alicorn|alicorn]] and 11- and 13-limit [[Unicorn family #Camahueto|camahueto]].
With [[3/1|harmonic 3]] less than a cent flat, [[5/1|harmonic 5]] a bit over three cents sharp and [[7/1|7]]'s less flat than that, 77edo represents an excellent tuning choice for both [[valentine]], the {{nowrap|31 & 46}} temperament, and [[starling]], the [[126/125]] [[planar temperament]], giving the [[optimal patent val]] for [[11-limit]] valentine and its [[13-limit]] extensions dwynwen and valentino, as well as 11-limit starling and [[oxpecker]] temperaments. It also gives the optimal patent val for [[grackle]] and various members of the [[unicorn family]], with a [[generator]] of 4\77 instead of the 5\77 (which gives valentine). These are 7-limit [[Unicorn family #Alicorn|alicorn]] and 11- and 13-limit [[Unicorn family #Camahueto|camahueto]].


77et tempers out [[32805/32768]] in the [[5-limit]], [[126/125]], [[1029/1024]] and [[6144/6125]] in the 7-limit, [[121/120]], [[176/175]], [[385/384]] and [[441/440]] in the 11-limit, and [[196/195]], [[351/350]], [[352/351]], [[676/675]] and [[729/728]] in the 13-limit.  
77et tempers out [[32805/32768]] in the [[5-limit]], [[126/125]], [[1029/1024]], and [[6144/6125]] in the 7-limit, [[121/120]], [[176/175]], [[385/384]], and [[441/440]] in the 11-limit, and [[196/195]], [[351/350]], [[352/351]], [[676/675]] and [[729/728]] in the 13-limit.  


The [[17/1|17]] and [[19/1|19]] are tuned fairly well, making it [[consistent]] to the no-11 [[21-odd-limit]]. The equal temperament tempers out [[256/255]] in the 17-limit; and [[171/170]], [[361/360]], [[513/512]], and [[1216/1215]] in the 19-limit.  
The [[17/1|17]] and [[19/1|19]] are tuned fairly well, making it [[consistent]] to the no-11 [[21-odd-limit]]. The equal temperament tempers out [[256/255]] in the 17-limit; and [[171/170]], [[361/360]], [[513/512]], and [[1216/1215]] in the 19-limit.  
Line 209: Line 209:
default [[File:77-EDO_Revo_Sagittal.svg]]
default [[File:77-EDO_Revo_Sagittal.svg]]
</imagemap>
</imagemap>
=== Ups and downs notation ===
Using [[Helmholtz–Ellis]] accidentals, 77edo can be notated using [[ups and downs notation]]:
{{Sharpness-sharp7}}


== Regular temperament properties ==
== Regular temperament properties ==
Line 343: Line 347:


== Zeta properties ==
== Zeta properties ==
===Zeta peak index===
=== Zeta peak index ===
{| class="wikitable"
{| class="wikitable"
! colspan="3" |Tuning
! colspan="3" |Strength
! colspan="2" |Closest EDO
! colspan="2" |Integer limit
|-
|-
!ZPI
! colspan="3" | Tuning
!Steps per octave
! colspan="3" | Strength
!Step size (cents)
! colspan="2" | Closest EDO
!Height
! colspan="2" | Integer limit
!Integral
!Gap
!EDO
!Octave (cents)
!Consistent
!Distinct
|-
|-
|[[414zpi]]
! ZPI
|76.9918536925042
! Steps per octave
|15.5860645308353
! Step size (cents)
|8.194847
! Height
|1.311364
! Integral
|17.029289
! Gap
|77edo
! EDO
|1200.12696887432
! Octave (cents)
|10
! Consistent
|10
! Distinct
|-
| [[414zpi]]
| 76.9918536925042
| 15.5860645308353
| 8.194847
| 1.311364
| 17.029289
| 77edo
| 1200.12696887432
| 10
| 10
|}
|}
== Music ==
== Music ==
; [[Jake Freivald]]
; [[Jake Freivald]]

Revision as of 02:32, 19 January 2025

← 76edo 77edo 78edo →
Prime factorization 7 × 11
Step size 15.5844 ¢ 
Fifth 45\77 (701.299 ¢)
Semitones (A1:m2) 7:6 (109.1 ¢ : 93.51 ¢)
Consistency limit 9
Distinct consistency limit 9

Template:EDO intro

Theory

With harmonic 3 less than a cent flat, harmonic 5 a bit over three cents sharp and 7's less flat than that, 77edo represents an excellent tuning choice for both valentine, the 31 & 46 temperament, and starling, the 126/125 planar temperament, giving the optimal patent val for 11-limit valentine and its 13-limit extensions dwynwen and valentino, as well as 11-limit starling and oxpecker temperaments. It also gives the optimal patent val for grackle and various members of the unicorn family, with a generator of 4\77 instead of the 5\77 (which gives valentine). These are 7-limit alicorn and 11- and 13-limit camahueto.

77et tempers out 32805/32768 in the 5-limit, 126/125, 1029/1024, and 6144/6125 in the 7-limit, 121/120, 176/175, 385/384, and 441/440 in the 11-limit, and 196/195, 351/350, 352/351, 676/675 and 729/728 in the 13-limit.

The 17 and 19 are tuned fairly well, making it consistent to the no-11 21-odd-limit. The equal temperament tempers out 256/255 in the 17-limit; and 171/170, 361/360, 513/512, and 1216/1215 in the 19-limit.

77edo is an excellent edo for Carlos Alpha, since the difference between 5 steps of 77edo and 1 step of Carlos Alpha is only −0.042912 cents.

Prime harmonics

Approximation of prime harmonics in 77edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31 37
Error Absolute (¢) +0.00 -0.66 +3.30 -2.59 -5.86 +1.03 +4.14 -1.41 -4.90 -1.01 -7.37 -1.99
Relative (%) +0.0 -4.2 +21.2 -16.6 -37.6 +6.6 +26.5 -9.0 -31.4 -6.5 -47.3 -12.8
Steps
(reduced) 		77
(0) 		122
(45) 		179
(25) 		216
(62) 		266
(35) 		285
(54) 		315
(7) 		327
(19) 		348
(40) 		374
(66) 		381
(73) 		401
(16)
Approximation of prime harmonics in 77edo (continued)
Harmonic 41 43 47 53 59 61 67 71 73 79 83 89
Error Absolute (¢) +7.30 +2.77 +4.62 -0.78 +0.57 +5.19 -1.38 +7.32 +5.98 -6.10 +1.90 +5.74
Relative (%) +46.8 +17.8 +29.7 -5.0 +3.6 +33.3 -8.9 +46.9 +38.4 -39.1 +12.2 +36.9
Steps
(reduced) 		413
(28) 		418
(33) 		428
(43) 		441
(56) 		453
(68) 		457
(72) 		467
(5) 		474
(12) 		477
(15) 		485
(23) 		491
(29) 		499
(37)

Intervals

Degree Cents Approximate Ratios*
0 0.000 1/1
1 15.584 81/80, 91/90, 99/98, 105/104
2 31.169 49/48, 55/54, 64/63, 65/64, 100/99
3 46.753 33/32, 36/35, 40/39, 45/44, 50/49
4 62.338 26/25, 27/26, 28/27
5 77.922 21/20, 22/21, 25/24
6 93.506 18/17, 19/18, 20/19
7 109.091 16/15, 17/16
8 124.675 14/13, 15/14
9 140.260 13/12
10 155.844 11/10, 12/11
11 171.429 21/19
12 187.013 10/9
13 202.597 9/8
14 218.182 17/15
15 233.766 8/7
16 249.351 15/13, 22/19
17 264.935 7/6
18 280.519 20/17
19 296.104 13/11, 19/16, 32/27
20 311.688 6/5
21 327.273 98/81
22 342.857 11/9, 17/14
23 358.442 16/13, 21/17
24 374.026 26/21, 56/45
25 389.610 5/4
26 405.195 19/15, 24/19, 33/26
27 420.779 14/11, 32/25
28 436.364 9/7
29 451.948 13/10
30 467.532 17/13, 21/16
31 483.117 120/91
32 498.701 4/3
33 514.286 27/20
34 529.870 19/14
35 545.455 11/8, 15/11, 26/19
36 561.039 18/13
37 576.623 7/5
38 592.208 24/17, 38/27, 45/32
… … …

* As a 19-limit temperament

Notation

Sagittal notation

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation81/8064/6333/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation81/8064/6333/32

Ups and downs notation

Using Helmholtz–Ellis accidentals, 77edo can be notated using ups and downs notation:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Sharp symbol  
Flat symbol

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [-122 77⟩ [⟨77 122]] +0.207 0.207 1.33
2.3.5 32805/32768, 1594323/1562500 [⟨77 122 179]] −0.336 0.785 5.04
2.3.5.7 126/125, 1029/1024, 10976/10935 [⟨77 122 179 216]] −0.021 0.872 5.59
2.3.5.7.11 121/120, 126/125, 176/175, 10976/10935 [⟨77 122 179 216 266]] +0.322 1.039 6.66
2.3.5.7.11.13 121/120, 126/125, 176/175, 196/195, 676/675 [⟨77 122 179 216 266 285]] +0.222 0.974 6.25

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 4\77 62.34 28/27 Unicorn / alicorn (77e) / camahueto (77) / qilin (77)
1 5\77 77.92 21/20 Valentine
1 9\77 140.26 13/12 Tsaharuk
1 15\77 233.77 8/7 Guiron
1 16\77 249.35 15/13 Hemischis (77e)
1 20\77 311.69 6/5 Oolong
1 23\77 358.44 16/13 Restles
1 31\77 483.12 45/34 Hemiseven
1 32\77 498.70 4/3 Grackle
1 34\77 529.87 512/375 Tuskaloosa
Muscogee
7 32\77
(1\77) 		498.70
(15.58) 		4/3
(81/80) 		Absurdity
11 32\77
(3\77) 		498.70
(46.75) 		4/3
(36/35) 		Hendecatonic

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Zeta properties

Zeta peak index

Tuning Strength Closest EDO Integer limit
ZPI Steps per octave Step size (cents) Height Integral Gap EDO Octave (cents) Consistent Distinct
414zpi 76.9918536925042 15.5860645308353 8.194847 1.311364 17.029289 77edo 1200.12696887432 10 10

Music

Jake Freivald
Joel Grant Taylor
Chris Vaisvil
Retrieved from "https://en.xen.wiki/index.php?title=77edo&oldid=177047"