User:Moremajorthanmajor/5L 2s (perfect eleventh-equivalent)
One way of distinguishing the 17/12 diatonic scale is by considering it a moment of symmetry scale produced by a chain of "fifths" (or "fourths") with the step combination of 5L 2s. Among the most well-known variants of this MOS proper are 17EDXIs diatonic scale along with both the Pythagorean diatonic scale and the various meantone systems. Other similar scales referred to by the term "diatonic" can be arrived at different ways – for example, through just intonation procedures, or with tetrachords. However, it should be noted that at least the majority of the other scales that fall under this category – such as the just intonation scales that use more than one size of whole tone – are actually JI detemperings or tempered approximations of them that both closely resemble and are derived from this MOS.
On the term diatonic
In TAMNAMS (which is the convention on all pages on scale patterns on the wiki), diatonic exclusively refers to 5L 2s. Other diatonic-based scales (specifically with 3 step sizes or more), such as Zarlino, blackdye and diasem, are called detempered (if the philosophy is RTT-based) or deregularized (RTT-agnostic) diatonic scales. The adjectives diatonic-like or diatonic-based may also be used to refer to diatonic-based scales, depending on what's contextually the most appropriate.
Substituting step sizes
The 5L 2s MOS scale has this generalized form.
- L L L s L L s
Insert 2 for L and 1 for s and you'll get the 12EDXI diatonic.
- 2 2 2 1 2 2 1
When L=3, s=1, you have 17EDXI of standard practice: 3 3 3 1 3 3 1
When L=3, s=2, you have 19EDXI: 3 3 3 2 3 3 2
When L=4, s=1, you have 22EDXI: 4 4 4 1 4 4 1
When L=4, s=3, you have 26EDXI: 4 4 4 3 4 4 3
When L=5, s=1, you have 27EDXI: 5 5 5 1 5 5 1
When L=5, s=2, you have 29EDXI: 5 5 5 2 5 5 2
When L=5, s=3, you have 31EDXI: 5 5 5 3 5 5 3
When L=5, s=4, you have 33EDXI: 5 5 5 4 5 5 4
So you have scales where L and s are nearly equal, which approach 7EDXI:
- 1 1 1 1 1 1 1
And you have scales where s becomes so small it approaches zero, which would give us 5EDXI:
- 1 1 1 0 1 1 0 = 1 1 1 1 1
Tuning ranges
Parasoft to ultrasoft
"17/12 Flattone" systems, such as 26EDXI.
Hyposoft
"17/12 Meantone" (more properly "septimal meantone") systems, such as 31EDXI.
Hypohard
The near-just part of the region is of interest mainly for those interested in 17/12 Pythagorean tuning and large, accurate EDO systems based on close-to-Pythagorean fifths, such as 41EDXI and 53EDXI. This class of tunings is called 17/12 schismic temperament; these tunings can approximate 517/12-limit harmonies very accurately by tempering out 17/12 of a small comma called the schisma. (Technically, 12EDXI tempers out the 17/12 schisma and thus is a 17/12 schismic tuning, but it is nowhere near as accurate as 17/12 schismic tunings can be.)
The sharp-of-just part of this range includes so-called "17/12 neogothic" or "17/12 parapyth" systems, which tune the 17/12 diatonic major third slightly sharply of 11/7 (around 128/81) and the diatonic minor third slightly flatly of 13/11 (around 32/27). Good 17/12 neogothic EDXIs include 29EDXI and 46EDXI. 17EDXI is often considered the sharper end of the neogothic spectrum; its major third at 800 cents is considerably more discordant than in flatter 17/12 neogothic tunings.
Parahard to ultrahard
"17/12 Archy" systems such as 17EDXI, 22EDXI, and 27EDXI.
Modes
17/12 Diatonic modes have standard names from classical music theory:
| Mode | UDP | Name |
|---|---|---|
| LLLsLLs | 6|0 | Lydian |
| LLsLLLs | 5|1 | Ionian |
| LLsLLsL | 4|2 | Mixolydian |
| LsLLLsL | 3|3 | Dorian |
| LsLLsLL | 2|4 | Aeolian |
| sLLLsLL | 1|5 | Phrygian |
| sLLsLLL | 0|6 | Locrian |
Scales
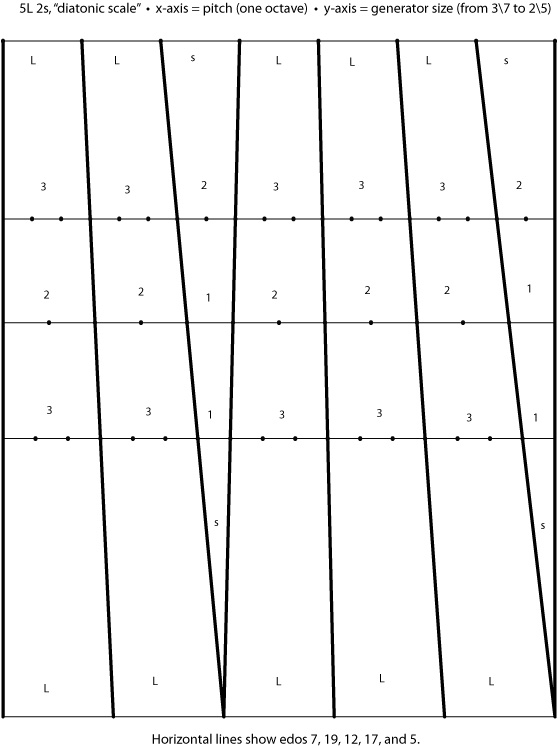
Scale tree
If 4\7 (four degrees of 7EDXI) is at one extreme and 3\5 (three degrees of 5EDXI) is at the other, all other possible 5L 2s scales exist in a continuum between them. You can chop this continuum up by taking "freshman sums" of the two edges - adding together the numerators, then adding together the denominators (i.e. adding them together as if you would be adding the complex numbers analogous real and imaginary parts). Thus, between 4\7 and 3\5 you have (4+3)\(7+5) = 7\12, seven degrees of 12EDXI.
If we carry this freshman-summing out a little further, new, larger EDXIs pop up in our continuum.
Generator ranges:
- Chroma-positive generator: 960 cents (4\7, normalized) to 1028.5714 cents (3\5, normalized)
- Chroma-negative generator: [[1]] cents (2\5, normalized) to 720 cents (3\7, normalized)
| Generator | Normalized | L | s | L/s | Comments |
|---|---|---|---|---|---|
| 4\7 | 960.000¢ | 1 | 1 | 1.000 | |
| 27\47 | 967.164¢ | 7 | 6 | 1.167 | |
| 23\40 | 968.421¢ | 6 | 5 | 1.200 | |
| 42\73 | 969.231¢ | 11 | 9 | 1.222 | |
| 19\33 | 970.213¢ | 5 | 4 | 1.250 | |
| 34\59 | 971.429¢ | 9 | 7 | 1.286 | |
| 15\26 | 972.972¢ | 4 | 3 | 1.333 | |
| 56\97 | 973.913¢ | 15 | 11 | 1.364 | |
| 41\71 | 974.2574¢ | 11 | 8 | 1.375 | |
| 67\116 | 974.54¢ | 18 | 13 | 1.385 | |
| 26\45 | 975.000¢ | 7 | 5 | 1.400 | 17/12 Flattone is in this region |
| 63\109 | 975.484¢ | 17 | 12 | 1.417 | |
| 37\64 | 975.824¢ | 10 | 7 | 1.429 | |
| 48\83 | 976.271¢ | 13 | 9 | 1.444 | |
| 11\19 | 977.7¢ | 3 | 2 | 1.500 | |
| 51\88 | 979.200¢ | 14 | 9 | 1.556 | |
| 40\69 | 979.592¢ | 11 | 7 | 1.571 | |
| 29\50 | 980.282¢ | 8 | 5 | 1.600 | |
| 76\131 | 980.645¢ | 21 | 13 | 1.615 | 17/12 Golden meantone (980.7157¢) |
| 47\81 | 980.870¢ | 13 | 8 | 1.625 | |
| 18\31 | 981.81¢ | 5 | 3 | 1.667 | 17/12 Meantone is in this region |
| 43\74 | 982.857¢ | 12 | 7 | 1.714 | |
| 25\43 | 983.607¢ | 7 | 4 | 1.750 | |
| 32\55 | 984.615¢ | 9 | 5 | 1.800 | |
| 39\67 | 985.263¢ | 11 | 6 | 1.833 | |
| 46\79 | 985.714¢ | 13 | 7 | 1.857 | |
| 53\91 | 986.047¢ | 15 | 8 | 1.875 | |
| 60\103 | 986.301¢ | 17 | 9 | 1.889 | |
| 67\115 | 986.503¢ | 19 | 10 | 1.900 | |
| 74\127 | 986.6¢ | 21 | 11 | 1.909 | |
| 81\139 | 986.802¢ | 23 | 12 | 1.917 | |
| 88\151 | 986.916¢ | 25 | 13 | 1.923 | |
| 95\163 | 987.013¢ | 27 | 14 | 1.929 | |
| 7\12 | 988.235¢ | 2 | 1 | 2.000 | Basic 17/12 diatonic (Generators smaller than this are proper) |
| 45\77 | 990.826¢ | 13 | 6 | 2.167 | |
| 38\65 | 991.304¢ | 11 | 5 | 2.200 | |
| 31\53 | 992.000¢ | 9 | 4 | 2.250 | The generator closest to 17/12 of a just 3/2 for EDXIs less than 200 |
| 55\94 | 992.481¢ | 16 | 7 | 2.286 | 17/12 Garibaldi / Cassandra |
| 24\41 | 993.103¢ | 7 | 3 | 2.333 | |
| 41\70 | 993.93¢ | 12 | 5 | 2.400 | |
| 58\99 | 994.2857¢ | 17 | 7 | 2.428 | |
| 17\29 | 995.122¢ | 5 | 2 | 2.500 | |
| 44\75 | 996.226¢ | 13 | 5 | 2.600 | |
| 71\121 | 996.491¢ | 21 | 8 | 2.625 | 17/12 Golden neogothic (996.3946¢) |
| 27\46 | 996.923¢ | 8 | 3 | 2.667 | 17/12 Neogothic is in this region |
| 37\63 | 997.753¢ | 11 | 4 | 2.750 | |
| 47\80 | 998.230¢ | 14 | 5 | 2.800 | |
| 57\97 | 998.540¢ | 17 | 6 | 2.833 | |
| 67\114 | 998.758¢ | 20 | 7 | 2.857 | |
| 77\131 | 998.918¢ | 23 | 8 | 2.875 | |
| 87\148 | 999.043¢ | 26 | 9 | 2.889 | |
| 10\17 | 1000.000¢ | 3 | 1 | 3.000 | |
| 43\73 | 1001.942¢ | 13 | 4 | 3.250 | |
| 33\56 | 1002.532¢ | 10 | 3 | 3.333 | |
| 23\39 | 1003.63¢ | 7 | 2 | 3.500 | |
| 36\61 | 1004.651¢ | 11 | 3 | 3.667 | |
| 49\83 | 1005.128¢ | 15 | 4 | 3.750 | |
| 13\22 | 1006.452¢ | 4 | 1 | 4.000 | 17/12 Archy is in this region |
| 55\93 | 1007.634¢ | 17 | 4 | 4.250 | |
| 42\71 | 1008.000¢ | 13 | 3 | 4.333 | |
| 29\49 | 1008.696¢ | 9 | 2 | 4.500 | |
| 45\76 | 1009.346¢ | 14 | 3 | 4.667 | |
| 16\27 | 1010.526¢ | 5 | 1 | 5.000 | |
| 51\86 | 1011.570¢ | 16 | 3 | 5.333 | |
| 35\59 | 1012.048¢ | 11 | 2 | 5.500 | |
| 19\32 | 1013.3¢ | 6 | 1 | 6.000 | |
| 41\69 | 1014.432¢ | 13 | 2 | 6.500 | |
| 22\37 | 1015.385¢ | 7 | 1 | 7.000 | |
| 3\5 | 1028.571¢ | 1 | 0 | → inf |
Tunings above 7\12 on this chart are called "negative tunings" (as they lessen the size of the fifth) and include 17/12 meantone systems such as 1/3-comma (close to 11\19) and 1/4-comma (close to 18\31). As these tunings approach 4\7, the majors become flatter and the minors become sharper.
Tunings below 7\12 on this chart are called "positive tunings" and they include 17/12 Pythagorean tuning itself (well approximated by 31\53) as well as 17/12 superpyth tunings such as 10\17 and 13\22. As these tunings approach 3\5, the majors become sharper and the minors become flatter. Around 13\22 through 16\27, the thirds fall closer to 5-limit than 7-limit intervals: 6:5 and 5:4 as opposed to 7:6 and 9:7.
5L 2s contains the pentatonic MOS 2L 3s and (with the sole exception of the 5L 2s of 12EDXI) is itself contained in a dodecaphonic MOS: either 7L 5s or 5L 7s, depending on whether the fifth is flatter than or sharper than 7\12 (988.235¢ normalized).
Related Scales
Because the diatonic scale is so widely used, it should be no surprise that there are a number of noteworthy scales of different sorts related to this MOS.