User:M-yac/Neutral Intervals and the FJS
A strength of the Functional Just System, or FJS, is that once you become familiar with an interval, its symbol is often obvious. For example, 6/5 is a minor third (it's the "classic minor third") and has a 5 in the denominator, so its symbol is "m3_5" - or 7/4 is a minor seventh (it's the "septimal minor seventh") and has a 7 in the numerator, so its symbol is "m7^7". But for neutral intervals, intervals which lie halfway between major and minor, this breaks down. For example, 12/11 is the "undecimal neutral second." Is its symbol "M2^11" or "m2^11"? What about another common neutral second, 11/10: is its symbol "M2^11_5" or "m2^11_5"? What I really want to do is write "n2^11" for the first and "n2^11_5" for the second! Is there a way for this to make sense?
This page presents a modification of the FJS in which those symbols do make sense, while still retaining most of the FJS's nice properties. This modification has two main parts:
- Extending the definition of Pythagorean interval in a natural way to include neutral intervals. In this extension, a Pythagorean neutral third, written "n3", is exactly (3/2)^(1/2), or sqrt(3/2).
- Lowering the FJS radius of tolerance. This ensures the formal comma of the 11th harmonic is a neutral interval (in particular, a semi-augmented fourth) which lets us write "n2_11" for 12/11, "n3^11" for 11/9, etc.
I call this modification the Neutral FJS, and you can experiment with it here or in xen-calc. Be sure to check out the table of examples at the end of the third section.
In the first section, I precisely define what a Pythagorean interval is, and in the second, show how to extend this definition naturally to include neutral intervals. If you don't care about the details, skip to the table at the end of the second section. In the third second, I give a brief overview of the FJS and discuss how to modify it. In the last two sections, we discuss the pros and cons of this modification and preview some generalizations.
Pythagorean intervals
A Pythagorean interval is an interval made up of only justly-tuned perfect fifths (3/2) and octaves (2/1). For example, a Pythagorean major second (9/8) is made by going two perfect fifths up and one octave down (i.e. 9/8 = (3/2) * (3/2) * (1/2)) and a perfect fourth (4/3) is made by going one perfect fifth down and one octave up (i.e. 4/3 = (2/3) * (2/1)).
Expressing this idea mathematically, we say that every Pythagorean interval has the form:
(3/2)^g * (2/1)^p
where g and p are integers. (In the language of rank-2 temperaments, g is the number of generators and p is the number of periods that make up the interval.)
The reason these intervals are so useful in systems like the FJS is that they have familiar names which are unique and consistent. Some of examples of these names are "P5" or "perfect fifth" for 3/2, "M2" or "major second" for 9/8, and "A6" or "augmented sixth" for 59049/32768 (= (3/2)^10 * (2/1)^(-5)).
More precisely, each Pythagorean interval has a unique degree and a unique quality. The former are positive whole numbers like 1, 2, 6, or 10 and the latter are symbols/names like "P"/"perfect", "M"/"major", or "d"/"diminished". The degree turns out to be easy to calculate from our mathematical definition of a Pythagorean interval: notice that adding a perfect fifth has the effect of raising the degree by 4 (e.g. two perfect fifths make a major ninth) and adding an octave raises the degree by 7 (e.g. a major second and an octave makes a major ninth). Our formula is thus:
d = 1 + 4*g + 7*p
For example, if g = 10 and p = -5, we have an interval with degree d = 1 + 4*10 + 7*(-5) = 6, and indeed this interval is the Pythagorean augmented sixth.
As for quality, notice that adding a multiple of 7 to g and subtracting the same multiple of 4 from p doesn't change the degree:
d_new = 1 + 4*(g + 7*k) + 7*(p - 4*k)
= 1 + 4*g + 28*k + 7*p - 28*k
= 1 + 4*g + 7*p
= d_old
Thus, the new interval defined by g+7*k and p-4*k must have a different quality! (If not, we would have two different Pythagorean intervals with exactly the same degree and quality, which we know we can't have.) In fact, this trick of adding a multiple of 7 to g and subtracting the same multiple of 4 from p can be used to find all the different qualities of intervals for a given degree. [1].
For Pythagorean intervals with "perfect" degrees, meaning ones with degree equal to 1, 4, or 5 plus a multiple of 7 (e.g. 1,4,5,8,11,12), the different qualities are named as follows:
... --> 2d -------> d (dim.) -------> P (perfect) -------> A (aug.) -------> 2A --> ...
g+7,p-4 g+7,p-4 g+7,p-4 g+7,p-4
and for the remaining intervals with "imperfect" degrees, the different qualities are:
... --> d (dim.) -------> m (minor) -------> M (Major) -------> A (aug.) --> ...
g+7,p-4 g+7,p-4 g+7,p-4
As a quick sanity check, the "Formula" column of the first table on the Wikipedia page for Pythagorean tuning tells us that a Pythagorean minor third is (3/2)^(-3) * (2/1)^2 (i.e. g = -3, p = 2). We should therefore expect a Pythagorean major third to have g = -3 + 7 = 4 and p = 2 - 4 = -2, and indeed we read off from that table that a Pythagorean major third is equal to (3/2)^4 * (2/1)^(-2).
Neutral Pythagorean intervals
Looking back at our formula for degree, notice that if g was a fraction like 1/2 we would still get what seems like a sensible answer for degree. For example, if g = 1/2 and p = 0 we get d = 3. But does it actually make sense to think of this interval as some kind of third?
Well, you probably know where I'm going with this: the answer is yes! The resulting interval is what I call a "Pythagorean neutral third" or "n3". Like other neutral thirds, it is roughly 350 cents (halfway between a 12-EDO major and minor third) and two of itself make a roughly a perfect fifth. In this case, two Pythagorean neutral thirds make exactly a perfect fifth ((3/2)^(1/2) * (3/2)^(1/2) = sqrt(3/2) * sqrt(3/2) = 3/2).
More generally, a Pythagorean interval with a non-integer value for g with denominator 2 I call a neutral Pythagorean interval. The degree of a neutral Pythagorean interval works exactly the same as for non-neutral Pythagorean intervals. As for quality, we can reach new "neutral" qualities by adding multiples of 7/2 to g instead of just 7 (and to balance this, subtracting multiples of 2 from p instead of 4). Our pictures for perfect and imperfect degrees now become:
... --> d ---------> sd ---------> P ---------> sA ---------> A --> ...
g+7/2,p-2 g+7/2,p-2 g+7/2,p-2 g+7/2,p-2
... --> d ---------> sd ---------> m ---------> n ---------> M ---------> sA ---------> A --> ...
g+7/2,p-2 g+7/2,p-2 g+7/2,p-2 g+7/2,p-2 g+7/2,p-2 g+7/2,p-2
where "sA" and "sd" stand for "semi-augmented" and "semi-diminished".
Here's a table of some notable neutral (in bold) and non-neutral Pythagorean intervals:
| Name | Symbol | Formula | Cents |
|---|---|---|---|
| perfect unison | P1 | 1/1 | 0.00 |
| semi-augmented unison | sA1 | (3/2)^(7/2) * (2/1)^(-2) | 56.84 |
| minor second | m2 | (3/2)^(-5) * (2/1)^3 | 90.22 |
| augmented unison | A1 | (3/2)^7 * (2/1)^(-4) | 113.68 |
| neutral second | n2 | (3/2)^(-3/2) * (2/1) | 147.06 |
| major second | M2 | (3/2)^2 * (2/1)^(-1) | 203.91 |
| minor third | m3 | (3/2)^(-3) * (2/1)^2 | 294.13 |
| neutral third | n3 | (3/2)^(1/2) | 350.97 |
| major third | M3 | (3/2)^4 * (2/1)^(-2) | 407.82 |
| semi-diminished fourth | sd4 | (3/2)^(-9/2) * (2/1)^3 | 441.20 |
| perfect fourth | P4 | (3/2)^(-1) * (2/1) | 498.04 |
| diminished fifth | d5 | (3/2)^(-6) * (2/1)^4 | 588.27 |
| augmented fourth | A4 | (3/2)^(6) * (2/1)^(-3) | 611.73 |
| perfect fifth | P5 | 3/2 | 701.96 |
| semi-augmented fifth | sA5 | (3/2)^(9/2) * (2/1)^(-2) | 758.79 |
| neutral sixth | n6 | (3/2)^(-1/2) * (2/1) | 849.02 |
| neutral seventh | n7 | (3/2)^(3/2) | 1052.93 |
| semi-diminished octave | sd8 | (3/2)^(-7/2) * (2/1)^(3) | 1143.15 |
| perfect octave | P8 | 2/1 | 1200.00 |
Modifying the FJS
First, a quick overview of how the FJS works - for more detail and explanations as to why this gives nice results, see misotanni's website.
- Octave-reduced prime intervals (i.e. 5/4, 7/4, 11/8, etc.) are associated with Pythagorean intervals using the "FJS master algorithm". This algorithm has two inputs: a radius of tolerance (RoT), which can be any interval, and a fifth sequence, whose entries are interpreted as values for g. The result of the algorithm is the first value for g in the sequence whose associated octave-reduced Pythagorean interval has a distance less than the RoT from the octave-reduced prime interval. In the standard FJS, the RoT is 65/63 and the fifths sequence is: 0, 1, -1, 2, -2, 3, -3, 4, -4, ..., 8, -8.
- For example, 5/4 is associated with the Pythagorean major third 81/64 (g = 4, p = -2). This is because 4 is the first value for g from our fifth sequence whose associated octave-reduced Pythagorean interval has a distance less than 65/63 from 5/4. In this case, the distance is (5/4) / (81/64) ≈ 21.5c, which is less than 65/63 ≈ 54.1c. The next closest value was g = -3, whose distance was (5/4) / (32/27) ≈ 92.2c.
- Each prime is given a formal comma, which is its octave-reduced interval divided by the Pythagorean interval to which it corresponds.
- For example, the prime 5 has the formal comma (5/4) / (81/64) = 80/81, the inverse of the syntonic comma.
- An FJS interval symbol is a Pythagorean interval followed by a series of prime accidentals, where otonal accidentals, written like "^p", mean you should multiply by the prime's formal comma, and utonal accidentals, written like "_p", mean you should divide by the prime's formal comma.
Note that in the FJS documentation and in my Custom FJS explorer, the values of g in the fifth sequence are referred to as fifth shifts.
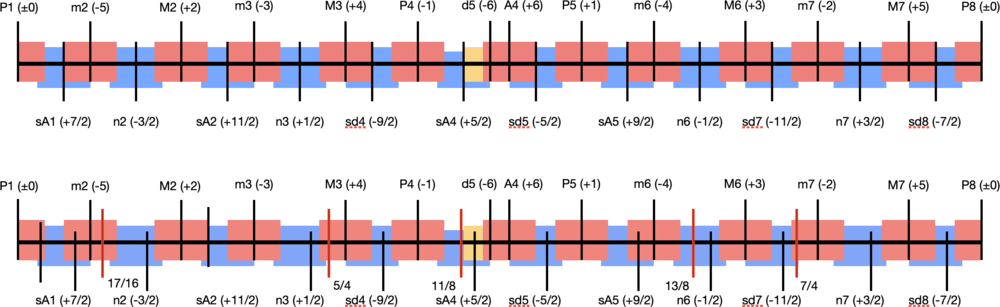
The first bullet above can also be understood visually. In the picture below, we start with a line representing the octave. Then, for each value of g in the fifth sequence, the octave-reduced Pythagorean interval corresponding to it is marked and a box is drawn around that mark which stretches 51c (the value of the RoT) in both directions. Regions defined by values later in the list will appear behind those defined by earlier ones, and overlaps are drawn using separate colors for clarity.
You can generate an interactive version of this image with my Custom FJS Explorer.
If we mark where 5/4 lies on this picture, we immediately know its associated Pythagorean interval has `g = 4`, since it falls inside the region marked with "M3 (+4)". In the picture below, 5/4 and a few other octave-reduced prime harmonics are marked.
We can also see in this picture that 5/4 is extremely well-approximated by a Pythagorean d4 (their difference is only 1.95c) but it is not associated with this interval since -8 comes after 4 in the fifth sequence. This is represented by the fact that the region marked with "d4 (-8)" is behind the region marked with "M3 (+4)".
Another thing to notice in the picture above is the tiny gaps that form between the m2 and M2 regions, m3 and M3 regions, and so on. As noted in User:FloraC/Critique on Functional Just System, this could be resolved by increasing the RoT.
To define the Neutral FJS, we make three changes to the standard FJS: 1. Allow the phrase "Pythagorean interval" to include neutral Pythagorean intervals, 2. Change the RoT to the Pythagorean semi-diminished 2nd (sd2), roughly 33.38c, 3. Change the fifth sequence to: 0, 1, -1, 2, -2, ..., 6, -6, 1/2, -1/2, 3/2, -3/2, ..., 11/2, -11/2.
Below are versions of the same two pictures as above but with these updated values for the RoT and fifths sequence.
This choice of fifth sequence just corresponds to the idea that when approximating prime harmonics, we should consider simple non-neutral Pythagorean intervals first, then consider neutral ones. The RoT chosen is exactly the distance between sA4 and d5 (or sA3 and M3, etc.), but any value roughly between 28.4c and the chosen RoT (33.4c) will have the same effect. An RoT any smaller than 28.4c will result in gaps popping up between non-neutral and neutral regions, and an RoT any larger than 33.4c will result in primes which closely approximate neutral intervals (e.g. 11/8) not actually getting assigned those neutral intervals (e.g. 11/8 getting assigned to a d5 if the RoT is more than a few cents larger than 33.4c).
Finally, here's a table of comparing some FJS and Neutral FJS interval symbols in the 11-limit and 13-limit (generated using xen-calc).
| Ratio | Name | FJS Symbol | Neutral FJS Symbol | Cents |
|---|---|---|---|---|
| 12/11 | undecimal neutral second | M2_11 | n2_11 | 150.63 |
| 11/10 | large undecimal neutral second | m2^11_5 | n2^11_5 | 165.00 |
| 11/9 | undecimal neutral third | m3^11 | n3^11 | 347.41 |
| 11/8 | undecimal super-fourth | P4^11 | sA4^11 | 551.32 |
| 13/12 | tridecimal neutral second | m2^13 | n2^13 | 138.57 |
| 13/11 | tridecimal minor third | m3^13_11 | m3^13_11 | 289.21 |
| 16/13 | tridecimal neutral third | M3_13 | n3_13 | 359.47 |
| 13/9 | tridecimal diminished fifth | d5^13 | sd5^13 | 636.62 |
| 13/8 | tridecimal neutral sixth | m6^13 | n6^13 | 840.53 |
| 14/11 | undecimal major third | P4^7_11 | sd4^7_11 | 417.51 |
| 14/13 | tridecimal 2/3-tone | M2^7_13 | n2^7_13 | 128.30 |
| 15/13 | tridecimal semi-fourth | A2^5_13 | sA2^5_13 | 247.74 |
| 13/10 | tridecimal semi-sixth | d4^13_5 | sd4^13_5 | 454.21 |
| 121/64 | Alpharabian major seventh | m7^11,11 | M7^11,11 | 1102.64 |
Comparing the FJS and Neutral FJS
Here are some positives that both systems have:
- Both have unique symbols for every JI ratio.
- I'd argue both are equally easy to learn and use.
The main advantage of the NFJS over the FJS is the fact that it can intuitively represent neutral intervals - see the introduction or the table in the previous section for some examples of this.
The main disadvantage of the NFJS is that unlike the FJS, it permits "bad" symbols which do not correspond to JI ratios. There are two cases: If a symbol's base Pythagorean interval is neutral, the symbol only corresponds to a JI ratio if all its prime accidentals correspond to neutral Pythagorean intervals. For example, n3^11 corresponds to a JI ratio (namely, 11/9), but n3^5 does not - it corresponds to whatever you want to call sqrt(3/2) * 80/81. If a symbol's base Pythagorean interval is non-neutral, the symbol only corresponds to a JI ratio if there are an even number of prime accidentals which correspond to neutral Pythagorean intervals. For example, m3^13_11 corresponds to a JI ratio (namely, 13/11), but m3^13 does not - it corresponds to whatever you want to call 32/27 * (13/8) / sqrt(8/3).
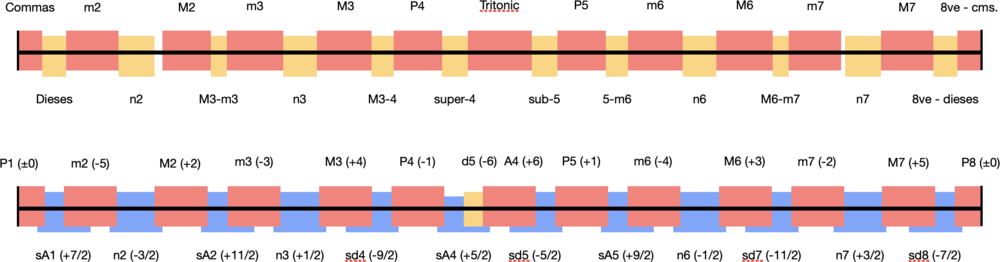
An advantage of the NFJS is that its RoT and fifth sequence result in a cleaner division of the octave compare to the FJS. In fact, the NFJS' division of the octave is almost exactly the same as that in Margo Schulter's Regions of the Interval Spectrum - they're within ±5 cents! In the image below, the regions on the top are exactly those defined in Schulter's article, and the regions on the bottom are exactly those defined by the NFJS.
Below is a table (hidden by default) of this same comparison.
| Schulter | Neutral FJS | ||
|---|---|---|---|
| Name | Region | Name | Region |
| Commas | 0c - 30c | P1 | 0.00c - 33.38c |
| Dieses | 30c - 60c | sA1 | 33.38c - 56.84c |
| m2 | 60c - 125c | m2 | 56.84c - 123.61c |
| n2 | 125c - 170c | n2 | 123.61c - 170.58c |
| M2 | 180c - 240c | M2 | 170.58c - 237.23c |
| M2-m3 | 240c - 260c | sA2 | 237.23c - 260.75c |
| m3 | 260c - 330c | m3 | 260.75c - 327.52c |
| n3 | 330c - 372c | n3 | 327.52c - 374.44c |
| M3 | 372c - 440c | M3 | 374.44c - 441.20c |
| M3-P4 | 440c - 468c | sd4 | 441.20c - 464.66c |
| P4 | 468c - 528c | P4 | 464.66c - 532.43c |
| super-4 | 528c - 560c | sA4 | 532.43c - 554.89c |
| Tritonic | 560c - 640c | d5 | 554.89c - 578.35c |
| A4 | 578.35c - 645.11c | ||
| sub-5 | 640c - 672c | sA5 | 645.11c - 668.58c |
| P5 | 672c - 732c | P5 | 668.58c - 735.34c |
| P5-m6 | 732c - 760c | sA5 | 735.34c - 758.34c |
| m6 | 760c - 828c | m6 | 758.34c - 825.56c |
| n6 | 828c - 870c | n6 | 825.56c - 872.48c |
| M6 | 870c - 940c | M6 | 872.48c - 939.25c |
| M6-m7 | 940c - 960c | sd7 | 939.25c - 962.71c |
| m7 | 960c - 1025c | m7 | 962.71c - 1029.47c |
| n7 | 1030c - 1075c | n7 | 1029.47c - 1076.39c |
| M7 | 1075c - 1140c | M7 | 1076.39c - 1143.16c |
| 8ve - diesis | 1140c - 1170c | sd8 | 1143.16c - 1166.62c |
| 8vs - commas | 1170c - 1200c | d8 | 1166.62c - 1200c |
Generalizing
Here are a few disjointed thoughts about how to generalize the contents of this article.
- It's a common convention that Pythagorean intervals with negative degrees are the inverses of those with positive degrees. For example, "P-5" refers to 2/3, the inverse of "P5", 3/2. This breaks our formula for degree in Section 1! For example, if g = -1 our formula tells us d = 1 + 4*(-1) = -3, while it should be -5. To fix this, we need to define the notion of zeroed degree, which is the degree minus its sign. For example, if d = 5, then the zeroed degree zd = 4, and if d = -5, then zd = -4. We then replace our original degree formula with the following two formulas:
zd = 4*g + 7*p and d = 1 + zd if zd >= 0, d = -1 + zd if zd < 0 - In Section 2, we noticed that if g was a rational number with denominator 2, our formula for degree didn't break. Well, notice that we could go one step further and let g be a rational number with denominator 4, and still nothing would break. I call these semi-neutral Pythagorean intervals and their quality spectrums now become:
... --> d --> 3/4-d --> sd --> 1/4-d --> P --> 1/4-A --> sA --> 3/4-A --> A --> ... ... --> d --> 3/4-d --> sd --> 1/4-d --> m --> sm --> n --> sM --> M --> 1/4-A --> sA --> 3/4-A --> A --> ...
where the arrows correspond to
g+7/4,p-1and "sM", "sm" stand for "semi-major", "semi-minor". As for "1/4-A", etc. perhaps they could be spoken as "quarter-augmented" or perhaps as "sesqui-augmented" as suggested on Shaahin Mohajeri's page about 96-EDO. - In Sections 1 and 2 I do not actually give a way to directly compute the quality from an arbitrary Pythagorean interval, only how to get every quality for a given degree assuming you already know g, p, and the quality of some interval of that degree. In my source code for microtonal_utils I give an algorithm for how to get the quality directly from g and p using a quantity I called the offset - see pyQuality in pythagorean.js.
- I only discuss interval symbols here, but it should be straightforward to extend the Neutral FJS to include note symbols as well, using the half-sharp, half-flat, etc. symbols to notate "neutral" Pythagorean-tuned notes. One big disadvantage of using the NFJS in this way for note symbols is that it would conflict with the 2020 HEJI, which otherwise works perfectly as an alternate notation for FJS notes.