User:Aura/Aura's Ideas on Functional Harmony (Part 1)
One construct from Western Classical music with potential implications for Microtonalists is harmonic function- especially as it pertains to the diatonic MOS scale and its various relatives. While in Mainstream Music Theory there are two prevailing schools of thought in regards to diatonic functional harmony- German Theory and Viennese Theory- ideas from both schools, as well as a number of other ideas, find a home in my microtonal theory and practice.
Facets Derived from German Theory
Among the chief ideas that come from German Theory is that there are three basic, or primary functions, and that there are multiple operations that can be applied to these three basic functions in order to derive new functions.
Basic Diatonic Functions
The three basic functions have their roots in LCJI, and are labeled as follows:
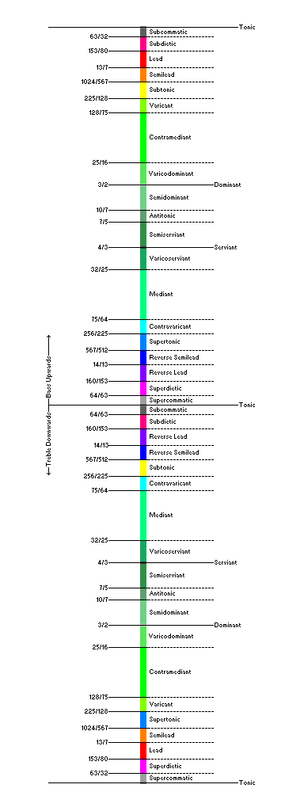
Tonic - This is the note that serves as the tonal center, and thus, the main resolution tone, and is the note for which scales are named (e.g. the key of C major is so-named because in this scale, C serves as the Tonic). This functionality has its roots in the fundamental at the root of both the Overtone and Undertone series, which for all intents and purposes, can be thought of as 1/1, and, in octave equivalent systems, 2/1. Beyond being simply one of the primary three functions in German Theory, it is the only function that is known to be universal when it comes to tonal music, with the various other functions being collectively defined as nontonic, thus, it shouldn't come as a great surprise that the Tonic exerts a very powerful influence on the context of functional harmony regardless of the nature of the tonal music system in question. In the realm of microtonality, the Tonic is not an interval that admits a lot of competition outside of modulation, and thus, deviations from a perfect 1/1 of up to 3.5 cents away from the Tonic are considered here to be found in the Tonic's "event horizon", in which they are either absorbed into the bandwidth of the Tonic itself, altered through fudging, or simply tempered out.
Dominant - As per the name, and as noted on the Wikipedia article, the Dominant is the second most important after the Tonic, though in contrast to what is stated about the Dominant in the article, there are several caveats which must be addressed in the realm of microtonality. Firstly, there are a variety of other intervals between 187/128 and 32/21 away from the Tonic in the scale's direction of construction which have the tendency to create tension which requires the Tonic to resolve. Thus, because of the extremely close harmonic connection between the Tonic and the 3/2 Perfect 5th, the term "Dominant"- in its most basic form as referred to in this article- is restricted to where it only refers to the such notes that occur roughly at a 3/2 interval away from the Tonic in the scale's direction of construction, with acceptable detuning levels being at around 3.5 cents from JI on either side. Secondly, the level of importance typically associated with the Dominant goes instead to a different note instead of a 3/2 Perfect 5th in scales where the 5th scale degree is too far away from 3/2. As for the notes at other intervals between 187/128 and 32/21, they shall be divided into two classes depending on which side of the 3/2 Perfect Fifth they fall on and discussed in another section. However, aside from 40/27, none of these other intervals occur in diatonic scales.
Serviant - Compared to the term "Subdominant" from traditional music theory, the term "Serviant" is restricted to those notes that occur roughly at a 4/3 interval away from the Tonic in the scale's direction of construction, and act as a sort of counterweight to the Dominant relative to the Tonic. Although one might think that the term "Subdominant" would be eligible for getting a similar treatment to the term "Dominant" here, the problems with such an option are two-fold. Firstly, not all possible "Subdominant" harmonies have the same harmonic properties relative to the Tonic, as there is an extremely close connection between the Tonic and the 4/3 Perfect 4th, and this is not the case for other intervals between 21/16 and 7/5. Secondly, in music built from the Treble downwards, the notes with these sorts of functions are actually located above the Dominant. Like with notes at other intervals between 21/16 and 256/187 away from the Tonic- the Serviant tends to resolve towards the Dominant, or else some other note that acts as a surrogate for the Dominant. As for the notes at other intervals between 21/16 and 256/187, they shall be divided into two classes depending on which side of the 4/3 Perfect 4th they fall on and discussed in another section. However, aside from 27/20, none of these other intervals occur in diatonic scales.
Basic Operations
The way I see it, there are at least four known operations which can be used to derive additional functions from the three basic functions listed above.
Stacking - The notes that are arrived at through stacking multiple instances of either 3/2 or 4/3 (or their tempered counterparts) are dubbed according to the number of instances stacked, and the nature of the notes separated by the interval being stacked. Thus, stacking two instances of the Dominant or the Serviant results in the creation of the "Double Dominant" or "Double Serviant" respectively. This concept comes from the German language's way of referring to the chord built on the second scale degree of the Diatonic scale as the "Doppeldominante", which literally means "Double Dominant".
Parallelism - Notes located in the same primary tetrachord as either the Tonic, the Dominant, or the Serviant take on similar functions to said notes, with the caveat that functions derived from the Tonic in this fashion are still technically nontonic functions. This process is one of two that create what in traditional music theory are referred to as "parallels" and "counter parallels".
Adjacency - Notes within a suitable voice leading distance from either the Dominant or Serviant tend to have the opposite function relative to the Tonic- this process even extends to the relationship between the Dominant and Serviant themselves. On the other hand, notes within this same kind of distance from the Tonic often tend to have their functions colored more by their relationships to both the Dominant and Serviant. This process is one of two that create what in traditional music theory are referred to as "parallels" and "counter parallels", however, unlike Parallelism proper, this process can establish these kinds of relationships outside the primary tetrachord.
Antipodism - Notes that are either opposite in tone color or nearly so due to being approximately half an octave away from the starting point are harmonically opposed to the starting point. Non-tonic notes related through this process tend to have the opposite function relative to the Tonic. For the notes related to the Tonic by this process see Antitonic below.
Facets Derived from Viennese Theory
Among the chief ideas that come from Viennese Theory is the idea that each degree has its own function relative to the Tonic. However, while in Viennese Theory proper, the degrees are strictly defined only relative to the cycle of fifths, I, for the realm of Microtonality, not only take stacks of 3/2 to form a key navigational axis called the "Diatonic Axis", but also additionally take things like Bass-Up Tonality (that is, music built from the Bass upwards) and Treble-Down Tonality (that is, music built from the Treble downwards) into consideration. On top of that, I also contend that virtually all of the functions described by Viennese Theory find their roots in specific combinations of the different operations described above on the basic functions from German Theory.
Derivative Diatonic Functions
I should point out that all of the scale degree functions described in Viennese Theory, as well as a few additional functions listed on this page, can be classified as first derivative functions because only one instance of any given derivational process is needed to reach them.
Contralead - This function, although not found in Viennese Theory proper, is easily derivable through a combination of the Tonic Adjacent function, the Subdominant Parallel function of 16/15, and the Antidominant function typified by the root of the Neapolitan chord. As such, this lowered second scale degree in Bass-Up Tonality should be considered as more than just a simple chromatic alteration of the Supertonic. Taking this idea into the realm of Microtonality, the Contralead is an interval that occurs at intervals between 25/24 and 14/13 away from the Tonic, and serves in part as a leading tone in the direction opposite that of the scale's direction of construction.
Supertonic - This function is easily derivable through a combination of the Tonic Adjacent function, the Subdominant Parallel function of 10/9 and Double Dominant function of 9/8, or at least that's the case in Bass-Up Tonality, and especially in meantone contexts where the two intervals are equated. However, I would argue that due to both the close proximity of 10/9 and 9/8 even in non-meantone settings and the shared Predominant functionalities of both scale degrees, these two functions often overlap to some degree or other. Accordingly, this is the note that occurs roughly at intervals between 567/512 and 256/225 above the Tonic as the second scale degree.
Mediant - This is the note that occurs roughly at intervals between 75/64 and 32/25 away from the Tonic in the scale's direction of construction, and is named due to being roughly halfway between the Tonic and the Dominant. This is the first of the two diatonic scale degrees with the most possibilities for realization. From a functional standpoint, the properties that are central to the Mediant function are all most easily derived through a combination of the Tonic Parallel function and the Serviant Adjacent function. However, there are other functional aspects of a Mediant that are determined by whether the interval in question is considered consonant or dissonant, with 5/4 and 6/5 being examples of consonant Mediants, and 81/64 and 32/27 being examples of dissonant Mediants.
Antitonic - This is a special case, see the next section for more discussion of this function.
Contramediant - Compared to the term "Submediant" from traditional music theory, the term "Contramediant" may have a slightly different frame of reference, as while a "Submediant" is halfway between the Tonic and a "Subdominant", the "Contramediant" is halfway between the Tonic and the Serviant. The Contramediant is a note that occurs roughly at intervals between 25/16 and 128/75 away from the Tonic in the scale's direction of construction, and is the second of two scale degrees with the most possibilities for the realization. From a functional standpoint, the properties that are central to the Contramediant function are most easily derived through a combination of the Tonic Parallel function and the Dominant Adjacent function. However, there are other functional aspects of a Contramediant that are determined by whether the interval in question is considered consonant or dissonant, with 5/3 and 8/5 being examples of consonant Contramediants, and 27/16 and 128/81 being examples of dissonant Contramediants.
Subtonic - This function is easily derivable through a combination of the Dominant Parallel function of 9/5 and Double Serviant function of 16/9, or at least that's the case in Bass-Up Tonality, and especially in meantone contexts where the two intervals are equated. As with the Supertonic, however, I would argue that due to both the close proximity of 9/5 and 16/9 even in non-meantone settings, these two functions often overlap to some degree or other. This is the note that occurs roughly at intervals between 225/128 and 1024/567 above the Tonic as the seventh scale degree.
Lead - This is the note typically referred to when people say "the leading tone", and, from a harmonic standpoint it is easily derivable through a combination of the Tonic Adjacent function, the Dominant Parallel function of 15/8, and the Antiserviant function. This is a note that occurs at intervals between 13/7 and 48/25 away from the Tonic, which serves as a leading tone in the scale's direction of construction. Although triads built on this scale degree are regarded by some as simply incomplete Dominant Seventh chords, my own analysis, while acknowledging the functional similarities between the Lead and the Dominant, sees this interval as functionally distinct from the Dominant due to the the Lead also being potentially related to the Mediant in the same way that the Dominant is related to the Tonic- a key functionality that is often exploited in circle progressions.
Antitonic
Notes that occur around half an octave away from the Tonic- especially the region extending from 7/5 to 10/7- on account of harmonies built on notes in this area tend to oppose that of the Tonic, thus leading to the term "Antitonic" being used to describe the region as a whole by myself and others. It should be noted that the Antitonic is basically a first derivative function as it is derived from the Tonic through either perfect or imperfect Antipodism. In addition, the term "Antitonic" acts as a generic term for any of a group of diatonic functions found in this region. While some microtonal theorists insist that the Antitonic functionality is more fundamental than perhaps even the Dominant or Serviant, others, such as myself, disagree.
Specific Types of Antitonic
The exact outcome and specific function of any given Antitonic depends on the interval between it and the Tonic in the scale's direction of construction, as well as by whether or not the interval in question is an augmented fourth or a diminished fifth:
- If the Antitonic is between 7/5 and 600 cents away from the Tonic and functions as an augmented fourth, it tends to cause the Dominant to become a new Tonic unless followed up by a different note- one that is usually a Major 7th away from the Tonic. Because of this tendency to "kiss up to" and tonicize the Dominant, this type of Antitonic can be dubbed a "Sycophant", with the prototypical Sycophant being 45/32.
- Conversely, if the Antitonic is between 600 cents and 10/7 away from the Tonic and functions as a diminished fifth, it tends to contrast with the Tonic in a manner somewhat akin to that of a Dominant, but by sheer brute force and contrary harmonic nature- e.g. if the Tonic harmony is Minor in nature, the Antitonic harmony will be Major- or more rarely, Supermajor- in nature. Furthermore, in scales such as the Locrian scale, any type of Serviant harmony tends to resolve towards either this type of Antitonic, or some other type of substitute for a Dominant. Because of these Dominant-esque tendencies, this type of Antitonic can be dubbed a "Tyrant", with the prototypical Tyrant being 64/45.
- If the Antitonic is between 7/5 and 600 cents away from the Tonic and functions as a diminished fifth, it demonstrates a mixture of both Sycophant-like and Tyrant-like properties, but because it is found just below the range of a typical Tyrant in Bass-Up Tonality, it is called a Gravotyrant in this kind of tonal systems. A classic example of such an interval is 1024/729.
- If the Antitonic is between 600 cents and 10/7 away from the Tonic and functions as an augmented fourth, it demonstrates a mixture of both Sycophant-like and Tyrant-like properties, but because it is found just above the range of a typical Sycophant in Bass-Up Tonality, it is called an Acuosycophant in this kind of tonal systems. A classic example of such an interval is 729/512.
Paradiatonic Functions
In addition to all the aforementioned Diatonic functions, there is an additional set of categories for dealing with the notes in between the various Diatonic scale degrees.
History
The idea of extending Diatonic functional harmony to cover intervals between the standard scale degrees is one that has at least some roots in Wyschnegradsky's concept of "Major Fourth" and "Minor Fifth". However, I wanted to use LCJI as a basis for defining these intervals and thus decided to take 11/8 as being the just version of Wyschnegradsky's "Major Fourth", and while I drew up sketches based loosely on 24edo for early versions of this concept, I also realized that that two instances of 33/32 added up to an interval smaller than 2187/2048 but which had a similar function. Furthermore, since two instances of 11/8 resulted in an interval in the vicinity of a Major seventh, I decided to takes stacks of 11/8 to form a second navigational axis which works together with the Diatonic Axis in order to define the microtonal functions positioned roughly halfway between the German and Viennese Diatonic functions, though there are a few other microtonal functions as well that are not immediately covered by this second axis.
Most traditional music theorists know that there are basically two types of semitones- the diatonic semitone or minor second, and the chromatic semitone or augmented prime. They also know that a diatonic semitone and a chromatic semitone add up to a whole tone. The same things are true in Just Intonation as well as in EDOs other than 12edo or even 24edo. In a conversation between myself and Kite Giedraitis about this topic, Kite mentioned that there are two types of semitone in 3-limit tuning- a diatonic semitone of with a ratio of 256/243, and the aforementioned 2187/2048- a chromatic semitone that is otherwise known as the Apotome- which, when added together, add up to a 9/8 whole tone. Furthermore, Kite also mentioned how in 5-limit tuning, these same semitones exist alongside other semitones derived through alteration by 81/80. On one hand, adding 81/80 to 256/243 yields 16/15, and adding another 81/80 yields 27/25- two additional diatonic semitones. On the other hand, subtracting 81/80 from the Apotome yields 135/128, and subtracting another 81/80 yields 25/24- two additional chromatic semitones. When added up in the proper pairs- 16/15 with 135/128, and 27/25 with 25/24- the additional sets of semitones again yield a 9/8 whole tone. In light of all this, Kite argued that the familiar sharp signs and flat signs- which are used to denote the chromatic semitone- were never meant to denote exactly half of a whole tone, but rather, a whole tone minus a minor second.
Building on Kite's logic, I then decided to apply similar distinctions among quartertones, and thus make the argument that quartertones don't have to denote exactly one fourth of a whole tone in as of themselves, but rather, they only have to add up to a whole tone when paired up correctly. However, the catch was that for quartertones, there are sometimes multiple correct options, making things more complicated. I decided to define the musical functions of quartertones initially on an informal basis by drawing a distinction between the terms "Parachromatic" (from the prefix para- in both the senses of alongside and resembling[1], and the word chromatic) and "Paradiatonic" (from the same two senses of the prefix para- and the word diatonic) for purposes of classifying quartertone intervals. This was easy, since after I found that two instances of 33/32 added up to 1089/1024 rather than 2187/2048, I had informally added the "para-" prefix (in the same senses) to both "Major" and "Minor" to create the terms Paramajor and Paraminor to better describe how 11/8 and 16/11 related to 128/99 and 99/64 respectively- namely to describe how, for instance, the notes at 99/64 and 16/11 above the Tonic relate to each other in much the same way as major and minor intervals do, except that this relationship occurs in a context where the note halfway between them is actually part of the base scale rather than the two notes in question, and there's a different interval between said two notes than the base scale's chroma.
The way I see it, paradiatonic quartertones are analogous to diatonic semitones in that they are denoted as seconds, albeit inframinor seconds by default, while parachromatic quartertones are analogous to chromatic semitones in that they are denoted as primes, albiet as ultraprimes by default. However, the distinction goes further than that- a parachromatic quartertone and a paradiatonic quartertone add up to a diatonic semitone, while two parachromatic quartertones add up to a chromatic semitone. Given both these definitions for "paradiatonic" and "parachromatic", and given that a diatonic semitone and a chromatic semitone add up to a whole tone when paired correctly, it can be deduced that a whole tone can be assembled from three parachromatic quartertones and one paradiatonic quartertone. Because there are sometimes multiple correct options for assembling parachromatic and paradiatonic intervals to make a 9/8 whole tone, I ended up choosing the simplest configuration of paradiatonic and parachromatic intervals to assemble in order to create a 9/8 whole tone- a configuration that only requires one type of parachromatic quartertone and one type of paradiatonic quartertone. As a result of multiple factors, I ended up choosing the combination of three 33/32 parachromatic quartertones and one 4096/3993 paradiatonic quartertone as the JI basis for this in regards to both Diatonic theory and Alpharabian tuning, and, through interactions with others in the Xenharmonic community, I was later influenced by others on Discord to take MOS-based structural considerations into account. This eventually resulted in the first formal definition of a "parachroma" (an interval that can be easily tempered to equal half of a MOS-chroma), and later, the "paralimma" (the interval that remains after subtracting as many parachromas from a Major MOS-step as possible without resulting in a negative interval). Finally, drawing from the concept of "parachromas" as applied to MOS-based contexts, I was able to finally give a formal definition of terms like "paramajor" (the result of adding a parachroma to either a MOS generator or its period-inverse) and "paraminor" (the result of subtracting a parachroma from a MOS generator or its period-inverse), which I had previously come up with on an informal basis.
Basic Paradiatonic Functions
As with the three basic diatonic functions, the two most basic basic paradiatonic functions have their roots in LCJI.
Intersubiant - This is a note that occurs roughly at intervals ranging from 256/187 to 25/18 away from the Tonic in the scale's direction of construction. Like both the Serviant and the Sycophant, intervals in this region tend to have a Predominant function, however, the way these intervals carry out this function is rather different from both as they neither act as a counterweight to the Dominant like a Serviant, nor do they completely tonicize the Dominant like a Sycophant- at least to those who are more familiar with quartertones. In Bass-Up tonality, this functionality has its roots in the eleventh harmonic, and indeed 11/8 is perhaps one of the best examples of an interval within this range.
Interregnant - This is a note that occurs roughly at intervals ranging from 36/25 to 187/128 away from the Tonic in the scale's direction of construction. Accordingly, intervals in this region behave as a cross between a Tyrant Antitonic on one hand and a Dominant on the other in that they often contrast with the Tonic through some combination of harmonic connection and brute force contrast. In Bass-Up tonality, this functionality has its roots in the eleventh subharmonic, and indeed 16/11 is perhaps one of the best examples of an interval within this range.
Interstep Functions
These intervals fall between the scale steps as defined by Viennese Theory, hence their collective label, and even some aspects of their individual names.
Varicant - Just as a Mediant lies roughly in the middle of the 3/2 interval separating the Tonic and the Dominant above it, a Varicant lies roughly in the middle of the 4/3 interval separating the Dominant and the Tonic above it. Intervals in this region often don’t consistently act as either sixths or sevenths, or even act as a cross between a sixth and a seventh- effectively straddling the border between these two diatonic categories, hence the name "Varicant", from Latin "vāricō"[2]. This is a note that occurs roughly at intervals between 128/75 and 225/128 away from the Tonic in the scale's direction of construction. In Bass-Up Tonality, this functionality is first encountered in the form of the 7/4 interval, though 12/7 is another notable interval included in this range. While many microtonalists think of 7/4 as being purely a type of seventh- and indeed, it most commonly acts as a sort of subminor seventh- I counterargue based on this same interval's relationships with 11/8 in particular that 7/4 is not merely a type of seventh, but rather, a type of a cross between a sixth and a seventh, with such a property explaining why 14/11 is generally considered to be a type of third.
Contravaricant - This is a note that occurs roughly at intervals between 256/225 and 75/64 away from the Tonic in the scale's direction of construction, lying roughly in the middle of the 4/3 interval separating the Tonic and the Serviant above it. Much like how intervals in the Varicant region often don’t consistently act as either sixths or sevenths, or even act as a cross between a sixth and a seventh, intervals in the Contravaricant region often don't consistently act as either seconds or thirds, or even act as a cross between a second and a third. In Bass-Up tonality, this functionality is first encountered in the form of 8/7, though 7/6 is another notable interval included in this range.
Varicodominant - This is a note that occurs roughly at intervals between 32/21 and 25/16 away from the Tonic in the scale's direction of construction. Accordingly, this region is characterized by intervals that don’t consistently act as either fifths or sixths, or even act as a cross between a fifth and a sixth, as well as by intervals that act as parachromatic alterations of either the Dominant or the Contramediant. The name of this region comes from "Varicant" and "Dominant", with a linking "-o-" in place of the "-ant" of "Varicant".
Varicoserviant - This is a note that occurs roughly at intervals between 32/25 and 21/16 away from the Tonic in the scale's direction of construction. Accordingly, this region is characterized by intervals that don’t consistently act as either thirds or fourths, or even act as a cross between a third and a fourth, as well as by intervals that act as parachromatic alterations of either the Mediant or the Serviant. The name of this region comes from "Varicant" and "Serviant", with a linking "-o-" in place of the "-ant" of "Varicant".
Neutral Degree Functions
While some neutralized scale degrees- such as the Neutral third and Neutral sixth- have the same diatonic functions as the adjacent Major and Minor scale degrees aside from always being dissonances, this is not the case for neutral seconds and neutral sevenths.
Semicontralead - This is a note that occurs roughly at intervals between 14/13 and 567/512 above the Tonic as the second scale degree. Naturally, this interval functions as a sort of cross between a Contralead and a Supertonic, and indeed chords built on this can function as some sort of cross between a Neapolitan chord and a Supertonic chord. However, there are ways in which the Semicontralead is distinct from both. Notably, set-ups and follow-ups for a Semicontralead- apart from root motion by a fifth- are generally best when moving in a given Tonality's direction of construction, as intervals like this moving stepwise in the opposite direction are likely to create a disjunct without proper context. The 12/11 neutral second is a rather typical example of an interval with this function.
Semilead - This is a note that occurs roughly at intervals between 1024/567 and 13/7 above the Tonic as the seventh scale degree. Naturally, this interval functions as a sort of Dominant Parallel, though there are significant differences from both a Subtonic and a Lead. For starters, a Semilead is likely to either resolve downwards to a Subtonic, or, upwards to either the Lead, the Tonic, or something in between, though in the latter case, it's subject to the same sorts of restrictions as a Semicontralead. The 11/6 neutral seventh is a rather typical example of an interval with this function.
Circumtonic Regions
The Circumtonic regions are the two main regions on either side of the Tonic, outside the Tonic's "event horizon". There are multiple paradiatonic functions hiding in these regions, though only two of them are really connected to the Tonic itself through stacking a combination 11/8 and 3/2 intervals.
Supercommatic - This is a note that occurs at intervals from about 3.5 cents to roughly 20 cents above the Tonic. These intervals are little more than stepping stones in modulation, and extra intervals that can be used together with the Tonic for a sense of dissonance, or for a slightly less resolved version of a Unison or Octave.
Superdietic - This is a note that occurs at intervals between roughly 20 cents above the Tonic and 25/24 above the Tonic. These intervals tend to act as parachromatic alterations of either the Tonic, or, in Bass-Up Tonality, the Contralead. However, while some microtonalists would question the idea of there being a distinct Superdietic region, preferring to think of the quartertones in this region as being simply the junction between the Supercommatic and Contralead regions, there there are actually a few functional differences between a Superdietic and a Contralead in Bass-Up Tonality that are worth considering. For starters, Superdietics are often more likely to be passing tones than Contraleads, and, when they’re not merely passing non-chord tones, they are just as liable to resolve upward thought some sort of semitone-like motion to some form of Contralead, Semicontralead, or even a Supertonic, as they are to resolve downwards toward the Tonic, a property which intervals like 33/32 in particular are apt to demonstrate. Furthermore, whereas a Contralead can resolve to the Tonic in part through a strong harmonic connection, a Superdietic is much more likely to do so through sheer brute force when such a resolution is noticeable.
Subdietic - This is a note that occurs at intervals between roughly 48/25 above the Tonic and roughly 20 cents below the octave reduplication of the Tonic. These intervals tend to act as parachromatic alterations of either the Tonic, or, in Bass-Up Tonality, the Lead- however, there are functional differences between a Subdietic and a Lead in Bass-Up Tonality. In Bass-Up Tonality, Subdietics are often more likely to be passing tones than Leads, and, when they’re not merely passing non-chord tones, they are often harder to approach and or follow up without creating some kind of awkward tonal disconnect, with such a disconnect being especially noticeable for intervals like 64/33. Furthermore, whereas a Lead can resolve to the Tonic in part through a strong harmonic connection, a Subdietic is much more likely to do so through sheer brute force, and even these cases require a proper set-up, as otherwise, the awkward tonal disconnect between the Subdietic and the Tonic is likely to result in the Subdietic resolving back down to either the Lead, the Semilead, or the Subtonic.
Subcommatic - This is a note that occurs at intervals from about 3.5 cents to roughly 20 cents below the Tonic. As with Supercommatic intervals, these intervals are little more than stepping stones in modulation, and extra intervals that can be used together with the Tonic for a sense of dissonance.
Additional Functions
In addition to the functions derived from both German theory and Viennese theory, as well as the Antitonic and Paradiatonic functions, I describe other functions here.
Circumdominant Regions
The circumdomimant regions are the two main regions on either side of the Dominant proper, and there are several functions located in these regions, one of which is an actual diatonic function. Note that antitonic and paradiatonic functions falling in this region are not covered in this section.
Mocktyrant - In Bass-Up Tonality, this is an interval that ranges from 13/10 to 7/5 which acts as a type of fifth rather than either a type of fourth or a type of third. These intervals are generally not that common outside of Jazz and Blues.
Acuotyrant - This is a note that occurs at intervals ranging from 10/7 to 36/25 away from the Tonic. Although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless operates more on the side of brute force when it contrasts with the Tonic.
Gravodominant - This is a note that occurs roughly at intervals ranging from 187/128 away from the Tonic to about 3.5 cents short of the 3/2 perfect fifth in the scale's direction of construction. Although often overlooked or even outright shunned by traditional theorists, I actually consider the Gravodominant to be a legitimate diatonic function- albeit one only existing in non-meantone environments. Specifically, as typified by intervals like 40/27, Gravodominants are dissonant intervals that simultaneously act as alternatives to the Dominant in both chord progressions and chord construction, and often require resolution. Apart from this, Gravodominants only rise to prominence in systems where what might otherwise function as a Dominant is found just short of the sweetspot range near the standard issue 3/2.
Acuodominant - This is a note that occurs roughly at intervals ranging from about 3.5 cents beyond the 3/2 perfect fifth to 32/21 away from the Tonic in the scale's direction of construction. These only rise to prominence in systems where what might otherwise function as a Dominant is found just beyond the sweetspot range near the standard issue 3/2.
Mockdominant - This is a note that occurs at intervals ranging from 32/21 to 64/39, specifically one which acts as a type of augmented fifth in contrast to a more typical function as a Contramediant, or else, acts as a surrogate for a note that would otherwise function as a Dominant. These only rise to prominence in systems where there’s no proper Dominant, and where what might otherwise function as a Dominant is found too far away from the standard issue 3/2. Beyond this, they tend mostly to be found in augmented chords, and in modes like Lydian Augmented in which the fifth is augmented.
Circumserviant Regions
The circumserviant regions are the two main regions on either side of the Serviant proper, and there are two functions located in these regions, one of which is an actual diatonic function. Note that antitonic and paradiatonic functions falling in this region are not covered in this section.
Mockserviant - This is a note that occurs at intervals ranging from 39/32 to 21/16, specifically one which acts as a type of diminished fourth in contrast to a more typical function as a Mediant, or else, acts as a surrogate for a note that would otherwise function as a Serviant. Thus, these intervals only rise to prominence either in modes like Superlocrian where the fourth is diminished or in systems where there’s no proper Serviant, and where what might otherwise function as a Serviant is found too far away from the standard issue 4/3.
Gravoserviant - This is a note that occurs roughly at intervals ranging from about 21/16 away from the Tonic to about 3.5 cents short of the 4/3 perfect fourth in the scale's direction of construction. These only rise to prominence in systems where what might otherwise function as a Serviant is found just short of the sweetspot range near the standard issue 4/3.
Acuoserviant - This is a note that occurs roughly at intervals ranging from 3.5 cents beyond the 4/3 perfect fourth to 256/187 away from the Tonic in the scale's direction of construction. As typified by intervals like 27/20, Acuoserviants are dissonant intervals that often act as a sort of predominant and or as the inverses of Gravodominants, making the Acuoserviant a legitimate diatonic function in terms of Aura's analysis. Apart from this, Acuoserviants only rise to prominence in systems where what might otherwise function as a Serviant is found just beyond the sweetspot range near the standard issue 4/3.
Gravosycophant - This is a note that occurs at intervals ranging from 25/18 to 7/5 away from the Tonic. Although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless often runs a high risk of tonicizing either the Dominant or the Gravodominant.
Mocksycophant - In Bass-Up Tonality, this is an interval that ranges from 10/7 to 20/13 which acts as a type of fourth rather than either a type of fifth or a type of sixth. These intervals are generally not that common outside of Jazz and Blues.
Differences from Neo-Riemannian Theory
<Section is a work in progress>
The lack of Meantone temperament has some pretty significant implications for triadic transformations voiceleading in my theory- namely in that not all of the three basic Neo-Riemannian transformations are available from just any tuning of a given Major or Minor triad, and conversely, that additional types of transformation are needed.