8edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
Xenwolf (talk | contribs)
autopatrolled, Bureaucrats, confirmaccount-notify, Interface administrators, Sysops
8,705 edits
m rem phone number linking
Xenllium (talk | contribs)
autopatrolled, emailconfirmed
4,516 edits
mNo edit summary
Line 10: Line 10:
| Fifth = 5\8 = 750¢
| Fifth = 5\8 = 750¢
| Major 2nd = 2\8 = 300¢
| Major 2nd = 2\8 = 300¢
| Minor 2nd = -1\8 = -150¢
| Augmented 1sn = 3\8 = 450¢
}}
}}
{{todo|add introduction}}


=Theory=
'''8 equal divisions of the octave''' ('''8EDO''') is the [[tuning system]] derived by dividing the [[octave]] into 8 equal steps of 150 [[cent]]s each, or the eighth root of 2.
 
= Theory =
{| class="wikitable center-all"
{| class="wikitable center-all"
! colspan="2" | <!-- empty cell -->
! colspan="2" | <!-- empty cell -->
Line 48: Line 47:
| +2
| +2
|-
|-
! colspan="2" | [[nearest edomapping]]
! colspan="2" | [[Patent val|nearest EDO-mapping]]
| 8
| 8
| 5
| 5
Line 69: Line 68:
|}
|}


8-edo forms an odd and even pitch set of two diminished seventh chords, which when used in combination yield dissonance. The system has been described as a "barbaric" harmonic system; even so, it does a good job representing the [[just intonation subgroup]]s 2.11/3.13/5, with good intervals of [[13/10]] and an excellent version of [[11/6]].
8EDO forms an odd and even pitch set of two diminished seventh chords, which when used in combination yield dissonance. The system has been described as a "barbaric" harmonic system; even so, it does a good job representing the [[just intonation subgroup]]s 2.11/3.13/5, with good intervals of [[13/10]] and an excellent version of [[11/6]].


Another way of looking at 8-EDO is to treat a chord of 0-1-2-3-4 degrees (0-150-300-450-600 cents) as approximating harmonics 10:11:12:13:14 (~0-165-316-454-583 cents), which is not too implausible if you can buy that 12-EDO is a 5-limit temperament. This interpretation would imply that 121/120, 144/143, 169/168, and hence also 36/35 and 66/65, are tempered out.
Another way of looking at 8EDO is to treat a chord of 0-1-2-3-4 degrees (0-150-300-450-600 cents) as approximating harmonics 10:11:12:13:14 (~0-165-316-454-583 cents), which is not too implausible if you can buy that 12EDO is a 5-limit temperament. This interpretation would imply that 121/120, 144/143, 169/168, and hence also 36/35 and 66/65, are tempered out.


=== Differences between distributionally-even scales and smaller edos ===
=== Differences between distributionally-even scales and smaller EDOs ===
{| class="wikitable"
{| class="wikitable"
|+
|+
Line 80: Line 79:
!s-Nedo
!s-Nedo
|-
|-
|3
| 3
|50¢
| 50¢
| -100¢
| -100¢
|-
|-
|5
| 5
|60¢
| 60¢
| -90¢
| -90¢
|-
|-
|6
| 6
|100¢
| 100¢
| -50¢
| -50¢
|-
|-
|7
| 7
|128.571¢
| 128.571¢
| -21.429¢
| -21.429¢
|}
|}


=Notation=
= Notation =
 
8EDO can be notated as a subset of 24EDO, using [[Ups_and_Downs_Notation|ups and downs]]. It can also be notated as a subset of 16EDO, but this is a less intuitive notation.
8-edo can be notated as a subset of 24-edo, using [[Ups_and_Downs_Notation|ups and downs]]. It can also be notated as a subset of 16-edo, but this is a less intuitive notation.


{| class="wikitable center-all"
{| class="wikitable center-all"
Line 106: Line 104:
! [[Cent]]s
! [[Cent]]s
! [[7mu]]s ([[Wikipedia: hexadecimal |hex]])
! [[7mu]]s ([[Wikipedia: hexadecimal |hex]])
! colspan="2" | 24-edo subset notation
! colspan="2" | 24EDO subset notation
! colspan="2" | 16-edo subset notation
! colspan="2" | 16EDO subset notation
|-
|-
| 0
| 0
Line 182: Line 180:
|}
|}


This is a heptatonic notation generated by 5ths (5th meaning 3/2). Alternative notations include pentatonic 5th-generated, octotonic, and heptatonic 2nd-generated.
This is a heptatonic notation generated by 5ths (5th meaning 3/2). Alternative notations include pentatonic 5th-generated, octatonic, and heptatonic 2nd-generated.


'''<u>Pentatonic 5th-generated</u>: D * E G * A C * D'''  (generator = 5\8 = perfect 5thoid)  
'''<u>Pentatonic 5th-generated</u>: D * E G * A C * D'''  (generator = 5\8 = perfect 5thoid)  
Line 209: Line 207:


== Chord Names ==
== Chord Names ==
[[Ups and Downs Notation#Chords and Chord Progressions|Ups and downs]] can name any 8-edo chord. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).  
[[Ups and Downs Notation #Chords and Chord Progressions|Ups and downs]] can name any 8EDO chord. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).  


8-edo chords are very ambiguous, with many chord homonyms. Even the major and minor triads are homonyms. Chord components usually default to M2, M3, P4, P5, M6, m7, M9, P11 and M13. Thus D7 has a M3, P5 and m7. 8-edo chord names using 24-edo subset names are greatly simplified by using different defaults: ~2, ^M3, v4, ^5, M6, ~7, ~9, v11 and M13. Thus D7 becomes ^M3, ^5 and ~7
8EDO chords are very ambiguous, with many chord homonyms. Even the major and minor triads are homonyms. Chord components usually default to M2, M3, P4, P5, M6, m7, M9, P11 and M13. Thus D7 has a M3, P5 and m7. 8-edo chord names using 24EDO subset names are greatly simplified by using different defaults: ~2, ^M3, v4, ^5, M6, ~7, ~9, v11 and M13. Thus D7 becomes ^M3, ^5 and ~7.


{| class="wikitable"
{| class="wikitable"
Line 264: Line 262:
|}
|}


=JI Intervals=
= JI Intervals =
[[File:8ed2-001.svg|alt=alt : Your browser has no SVG support.]]
[[File:8ed2-001.svg|alt=alt : Your browser has no SVG support.]]


Line 270: Line 268:


= Commas =
= Commas =
8 EDO [[tempers out]] the following [[comma]]s. This assumes [[val]] {{val| 8 13 19 22 28 30 }}.
8EDO [[tempers out]] the following [[comma]]s. This assumes [[val]] {{val| 8 13 19 22 28 30 }}.


{| class="commatable wikitable center-all left-3 right-5 left-6"
{| class="commatable wikitable center-all left-3 right-5 left-6"
Line 373: Line 371:
<references/>
<references/>


=Scala scale file=
= Scala scale file =
For those who use the new tuner Lingot, which accepts scala files, or for anyone else, here is a .scl file of 8 EDO [[:File:08-EDO.scl|08-EDO.scl]]
For those who use the new tuner Lingot, which accepts scala files, or for anyone else, here is a .scl file of 8EDO [[:File:08-EDO.scl|08-EDO.scl]]


0. 1/1 C Unison
0. 1/1 C Unison


1. 150.000 cents C# (50 cents sharper than C# of 12 tet) Neutral 2nd
1. 150.000 cents C# (50 cents sharper than C# of 12-TET) Neutral 2nd


2. 300.000 cents D# Minor 3rd (identical to 12-tet)
2. 300.000 cents D# Minor 3rd (identical to 12-TET)


3. 450.000 cents E Sub-4th, Supermajor 3rd (50 cents sharper than E of 12 tet)
3. 450.000 cents E Sub-4th, Supermajor 3rd (50 cents sharper than E of 12-TET)


4. 600.000 cents F# Tritone (identical to 12-tet)
4. 600.000 cents F# Tritone (identical to 12-TET)


5. 750.000 cents G Super 5th, Subminor 6th (50 cents sharper than G of 12 tet)
5. 750.000 cents G Super 5th, Subminor 6th (50 cents sharper than G of 12-TET)


6. 900.000 cents A Major 6th (identical to 12-tet)
6. 900.000 cents A Major 6th (identical to 12-TET)


7. 1050.000 cents A# Neutral 7th (50 cents sharper than A# of 12 tet)
7. 1050.000 cents A# Neutral 7th (50 cents sharper than A# of 12-TET)


8. 2/1 C Octave
8. 2/1 C Octave


==Pathological Modes==
== Pathological Modes ==
2 1 1 1 1 1 1 [[1L 6s]] MOS
2 1 1 1 1 1 1 [[1L 6s]] MOS
=Compositions=
= Compositions =
[https://soundcloud.com/overtoneshock/tenacious-chorale-9-edo-and-8-edo-live?in=overtoneshock/sets/xenharmonic-microtonal Tenacious Chorale (only movement II is in 8-EDO)] by Stephen Weigel
[https://soundcloud.com/overtoneshock/tenacious-chorale-9-edo-and-8-edo-live?in=overtoneshock/sets/xenharmonic-microtonal Tenacious Chorale (only movement II is in 8-EDO)] by Stephen Weigel


Line 425: Line 423:
[[:File:octo-icy-pensive(sketch).ogg|octo-icy-pensive(sketch).ogg]] [[:File:octo-icy-pensive-echo(sketch).ogg|octo-icy-pensive-echo(sketch).ogg]]2 versions of the same song, one with echo, one without. (cenobyte)
[[:File:octo-icy-pensive(sketch).ogg|octo-icy-pensive(sketch).ogg]] [[:File:octo-icy-pensive-echo(sketch).ogg|octo-icy-pensive-echo(sketch).ogg]]2 versions of the same song, one with echo, one without. (cenobyte)


=Ear Training=
= Ear Training =
8 EDO ear-training exercises by Alex Ness available [https://drive.google.com/a/playgroundsessions.com/folderview?id=0BwsXD8q2VCYUamtVWEgyRFA5alU&usp=sharing#list here].
8 EDO ear-training exercises by Alex Ness available [https://drive.google.com/a/playgroundsessions.com/folderview?id=0BwsXD8q2VCYUamtVWEgyRFA5alU&usp=sharing#list here].


=See also=
= See also =
*[[Octatonic_scale|Octatonic scale]] - a scale based on alternating whole and half steps
*[[Octatonic scale]] - a scale based on alternating whole and half steps


[[Category:8edo| ]] <!-- main article -->
[[Category:8edo| ]] <!-- main article -->
Line 436: Line 434:
[[Category:Listen]]
[[Category:Listen]]
[[Category:Macrotonal]]
[[Category:Macrotonal]]
[[Category:todo:unify_precision]]

Revision as of 13:56, 13 October 2021

← 7edo 8edo 9edo →
Prime factorization 23
Step size 150 ¢ 
Fifth 5\8 (750 ¢)
Semitones (A1:m2) 3:-1 (450 ¢ : -150 ¢)
Consistency limit 5
Distinct consistency limit 3

8 equal divisions of the octave (8EDO) is the tuning system derived by dividing the octave into 8 equal steps of 150 cents each, or the eighth root of 2.

Theory

prime 2 prime 3 prime 5 prime 7 prime 11 prime 13 prime 17 prime 19
error absolute (¢) 0 +48.0 +63.7 -68.8 +48.7 +59.5 +45.0 +2.5
relative (%) 0 +32 +42 -46 +32 +40 +30 +2
nearest EDO-mapping 8 5 3 6 4 6 1 2
fifthspan 0 +1 -1 -2 +4 -2 -3 +2

8EDO forms an odd and even pitch set of two diminished seventh chords, which when used in combination yield dissonance. The system has been described as a "barbaric" harmonic system; even so, it does a good job representing the just intonation subgroups 2.11/3.13/5, with good intervals of 13/10 and an excellent version of 11/6.

Another way of looking at 8EDO is to treat a chord of 0-1-2-3-4 degrees (0-150-300-450-600 cents) as approximating harmonics 10:11:12:13:14 (~0-165-316-454-583 cents), which is not too implausible if you can buy that 12EDO is a 5-limit temperament. This interpretation would imply that 121/120, 144/143, 169/168, and hence also 36/35 and 66/65, are tempered out.

Differences between distributionally-even scales and smaller EDOs

N L-Nedo s-Nedo
3 50¢ -100¢
5 60¢ -90¢
6 100¢ -50¢
7 128.571¢ -21.429¢

Notation

8EDO can be notated as a subset of 24EDO, using ups and downs. It can also be notated as a subset of 16EDO, but this is a less intuitive notation.

Edostep Cents 7mus (hex) 24EDO subset notation 16EDO subset notation
0 0¢ 0 P1 D P1 D
1 150 192 (C0) ~2 vE M2 E
2 300 384 (180) m3 F M3 F#
3 450 576 (240) ^M3 / v4 ^F# / vG d3 / A4 Fb / G#
4 600 768 (300) A4 / d5 G# / Ab d4 / A5 Gb / A#
5 750 960 (3C0) ^5 / vm6 ^A / vBb d5 / A6 Ab / B#
6 900 1152 (480) M6 B m6 Bb
7 1050 1344 (540) ~7 ^C m7 C
8 1200 1536 (600) P8 D P8 D

This is a heptatonic notation generated by 5ths (5th meaning 3/2). Alternative notations include pentatonic 5th-generated, octatonic, and heptatonic 2nd-generated.

Pentatonic 5th-generated: D * E G * A C * D (generator = 5\8 = perfect 5thoid)

D - D#/Eb - E - G - G#/Ab - A - C - C#/Db - D

P1 - A1/ms3 - Ms3 - P4d - A4d/d5d - P5d - ms7 - Ms7/d8d - P8d (s = sub-, d = -oid)

pentatonic genchain of 5ths: ...Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E#...

pentatonic genchain of 5ths: ...d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1... (s = sub-, d = -oid)

Octatonic: A B C D E F G H A (every interval is a generator)

P1 - P2 - P3 - P4 - P5 - P6 - P7 - P8 - P9

Heptatonic 2nd-generated: D E F G * A B C D (generator = 1\8 = perfect 2nd = 150¢)

D - E - F - G - G#/Ab - A -B - C - D

P1 - P2 - m3 - M3/m4 - M4/m5 - M5/m6 - M6 - P7 - P8

genchain of 2nds: ...D# - E# - F# - G# - A - B - C - D - E - F - G - Ab - Bb - Cb - Db...

genchain of 2nds: ...A1 - A2 - M3 - M4 - M5 - M6 - P7 - P1 - P2 - m3 - m4 - m5 - m6 - d7 - d8...

Chord Names

Ups and downs can name any 8EDO chord. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).

8EDO chords are very ambiguous, with many chord homonyms. Even the major and minor triads are homonyms. Chord components usually default to M2, M3, P4, P5, M6, m7, M9, P11 and M13. Thus D7 has a M3, P5 and m7. 8-edo chord names using 24EDO subset names are greatly simplified by using different defaults: ~2, ^M3, v4, ^5, M6, ~7, ~9, v11 and M13. Thus D7 becomes ^M3, ^5 and ~7.

Chord edosteps Chord notes Full name Abbreviated name Homonyms
0 – 3 – 5 D ^F♯ ^A D^(^5) D ^F♯m or vGm
0 – 2 – 5 D F ^A Dm(^5) Dm ^A or vB♭
0 – 3 – 5 – 7 D ^F♯ ^A ^C D^7(^5) D7 ^F♯m♯11 or vGm♯11
0 – 3 – 5 – 6 D ^F♯ ^A B D6(^3,^5) D6 Bm7 and vG,♯9
0 – 2 – 5 – 7 D F ^A ^C Dm,~7(^5) Dm7 F6 and vB♭,♯9
0 – 2 – 5 – 6 D F ^A B Dm6(^5) Dm6 Bm7(♭5)
0 – 2 – 4 – 7 D F A♭ ^C Ddim,~7 Dm7(♭5) Fm6

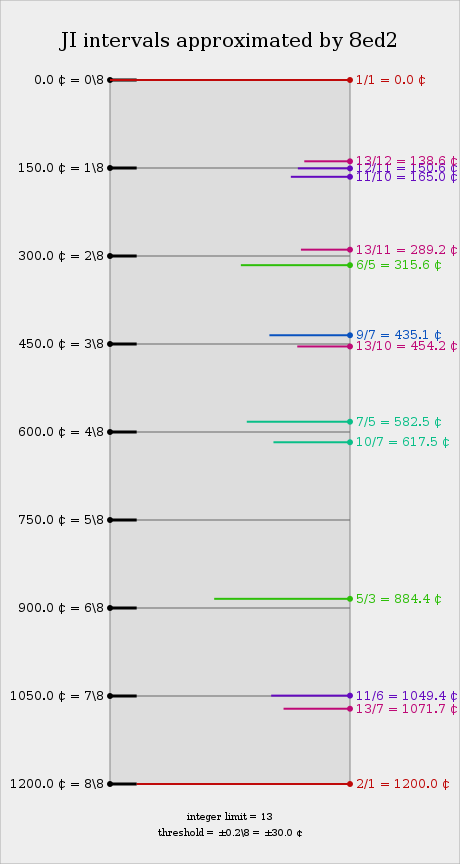
JI Intervals

alt : Your browser has no SVG support.

8ed2-001.svg

Commas

8EDO tempers out the following commas. This assumes val ⟨8 13 19 22 28 30].

Prime
Limit 		Ratio[1] Monzo Cents Color name Name(s)
5 648/625 [3 4 -4⟩ 62.57 Quadgu Major diesis, diminished comma
5 250/243 [1 -5 3⟩ 49.17 Triyo Maximal diesis, porcupine comma
5 78732/78125 [2 9 -7⟩ 13.40 Sepgu Medium semicomma, sensipent comma
7 64/63 [6 -2 0 -1⟩ 27.26 Ru Septimal comma, Archytas' comma, Leipziger Komma
7 875/864 [-5 -3 3 1⟩ 21.90 Zotriyo Keema
7 (12 digits) [-9 8 -4 2⟩ 8.04 Labizogugu Varunisma
7 6144/6125 [11 1 -3 -2⟩ 5.36 Sarurutrigu Porwell
11 100/99 [2 -2 2 0 -1⟩ 17.40 Luyoyo Ptolemisma
11 121/120 [-3 -1 -1 0 2⟩ 14.37 Lologu Biyatisma
11 176/175 [4 0 -2 -1 1⟩ 9.86 Lorugugu Valinorsma
11 65536/65219 [16 0 0 -2 -3⟩ 8.39 Satrilu-aruru Orgonisma
11 385/384 [-7 -1 1 1 1⟩ 4.50 Lozoyo Keenanisma
11 4000/3993 [5 -1 3 0 -3⟩ 3.03 Triluyo Wizardharry
  1. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Scala scale file

For those who use the new tuner Lingot, which accepts scala files, or for anyone else, here is a .scl file of 8EDO 08-EDO.scl

0. 1/1 C Unison

1. 150.000 cents C# (50 cents sharper than C# of 12-TET) Neutral 2nd

2. 300.000 cents D# Minor 3rd (identical to 12-TET)

3. 450.000 cents E Sub-4th, Supermajor 3rd (50 cents sharper than E of 12-TET)

4. 600.000 cents F# Tritone (identical to 12-TET)

5. 750.000 cents G Super 5th, Subminor 6th (50 cents sharper than G of 12-TET)

6. 900.000 cents A Major 6th (identical to 12-TET)

7. 1050.000 cents A# Neutral 7th (50 cents sharper than A# of 12-TET)

8. 2/1 C Octave

Pathological Modes

2 1 1 1 1 1 1 1L 6s MOS

Compositions

Tenacious Chorale (only movement II is in 8-EDO) by Stephen Weigel

Fantasia in 8ET[dead link] by Aaron Andrew Hunt

Fugue in 8ET[dead link] by Aaron Andrew Hunt

Špendlíky play by Milan Guštar

Acoustic Improvisation in 8-edo by Ron Sword (dead link)

Comets Over Flatland 7 by Randy Winchester

Malebolge Alison Jones

News To Me Jake Sherman

Tomorrow Night (pop music from 2045) Jake Sherman

FunkEight 1 by Carlo Serafini (blog entry)

8edo-pre-improv.oggPreliminary noodling in 8 EDO with ZynAddSubFX synth.(by Cenobyte)

darkreflections(sketch).ogg8EDO Ukulele (cenobyte)

skiphop(sketch).ogg8EDO Ukulele (cenobyte)

octo-icy-pensive(sketch).ogg octo-icy-pensive-echo(sketch).ogg2 versions of the same song, one with echo, one without. (cenobyte)

Ear Training

8 EDO ear-training exercises by Alex Ness available here.

See also

Retrieved from "https://en.xen.wiki/index.php?title=8edo&oldid=79473"