Spiral chart

A spiral chart is an illustration which converts a circle of repeats of an interval in one edo (or simply a temperament-agnostic chain of that interval) into a self-similar spiral shape, so that it may be compared with a circle of the same interval in a (smaller) coprime edo.

Spiral charts were first known to be used by Jeff Jensen in 2004, to describe the chain of fifths as it relates to 12edo. Much of the theory on this page, however, comes from Kite Giedraitis, no later than April 2014

Spirals of twelve fifths

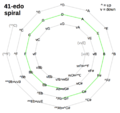
The spiral charts for 31edo, 41edo and 53edo relate each of those edos to 12edo via their chains of fifths. Thus, each chart has 12 spokes.

The larger edo's spiral of fifths is not really a spiral, it's a larger circle of fifths that is broken into a chain to make several smaller 12-note loops. Then a few duplicates are added at each end of the chain, so that one can reconnect the ends mentally to get the original larger circle. For the general case of fifth tunings that are not edos, the spiral is a true infinite spiral.

A 12-spoke spiral chart of fifths makes the most sense if, after going around by 12 fifths, the resulting interval differs by a very small amount, such as a comma or a single edostep. A 12-spoke spiral of semitones works for edos of the form 12n+1 or 12n-1, but those spirals are less interesting because they convey very little info that isn't already in the table of edosteps.

Gallery

• 
  31edo spiral chart
• 
  41edo spiral chart
• 
  41edo spiral chart (notation)
• 
  53edo spiral chart

The same information can be presented as a table. To follow the circle of 5ths, read the columns left to right, and within each column read top to bottom.

41edo intervals as a circle of 5ths, grouped into 12 categories

Tritones		vd5 = ~4 = 556¢	d5 = vA4 = 585¢	^d5 = A4 = 615¢	~5 = ^A4 = 644¢
Minorish 2nds		vm2 = 59¢	m2 = 88¢	^m2 = 117¢	~2 = 146¢
Minorish 6ths		vm6 = 761¢	m6 = 790¢	^m6 = 820¢	~6 = 849¢
Minorish 3rds		vm3 = 263¢	m3 = 293¢	^m3 = 322¢	(~3)
Minorish 7ths		vm7 = 966¢	m7 = 995¢	^m7 = 1024¢	(~7)
Perfectish 4ths		v4 = 468¢	P4 = 498¢	^4 = 527¢
Perfectish 1sns / 8ves		v8 = 1171¢	P1 = 0¢	^1 = 29¢
Perfectish 5ths		v5 = 673¢	P5 = 702¢	^5 = 732¢
Majorish 2nds	(~2)	vM2 =176 ¢	M2 = 205¢	^M2 = 234¢
Majorish 6ths	(~6)	vM6 = 878¢	M6 = 907¢	^M6 = 937¢
Majorish 3rds	~3 = 351¢	vM3 = 380¢	M3 = 410¢	^M3 = 439¢
Majorish 7ths	~7 = 1054¢	vM7 = 1083¢	M7 = 1112¢	^M7 = 1141¢
Tritones	~4 = vd5 = 556¢	vA4 = d5 = 585¢	A4 = ^d5 = 615¢	^A4 = ~5 = 644¢

Spirals of other amounts, other intervals

Such a spiral chart can be made for any two edos, as long as they are coprime; the interval that makes the most sense to choose in this case is the closest interval between the two edos, called the "near miss", because that results in a small comma alteration once you go around by the smaller edo's size in the larger edo (like fifths in 31edo).

For example, consider 8edo and 27edo. The near misses are 3\8 and 10\27. You get an 8-spoke spiral of 27edo major 3rds. This might be useful for someone researching octatonic scales in 27edo. To follow the circle of 3rds, read the columns left to right, and within each column read top to bottom.

27edo intervals as a circle of major 3rds, grouped into 8 categories

Tritones		A4 = v5	vA4 = vv5	^^4 = ^d5	^4 = d5
Middish 7ths		vM7	~7	^m7	m7
Minorish 3rds		~3	^m3	m3	(M2)
Minorish 6ths		^m6	m6	vm6
Perfectish 1sns / 8ves		^1	P1	v8
Majorish 3rds		^M3	M3	vM3
Majorish 6ths	(m7)	M6	vM6	~6
Middish 2nds	M2	vM2	~2	^m2
Tritones	A4 = v5	vA4 = vv5	^^4 = ^d5	^4 = d5

Relationship to the scale tree

Todo: complete section

See also

• Circle of fifths
• Scale tree