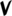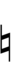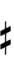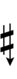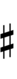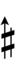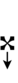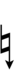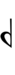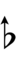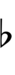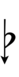55edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
m →Theory: Fix links to Mohajira and Liese
 
(31 intermediate revisions by 9 users not shown)
Line 1: Line 1:
{{interwiki
{{interwiki
| de =  
| de = 55-EDO
| en = 55edo
| en = 55edo
| es = 55 EDO
| es = 55 EDO
Line 6: Line 6:
}}
}}
{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|55}}
{{ED intro}}


== Theory ==
== Theory ==
55edo can be used for a [[meantone]] tuning, and is close to [[1/6-comma meantone]] (and is almost exactly 10/57-comma meantone). {{w|Georg Philipp Telemann|Telemann}} suggested it as a theoretical basis for analyzing the [[meantone intervals|intervals of meantone]]. {{w|Leopold Mozart|Leopold}} and {{w|Wolfgang Amadeus Mozart|Wolfgang Mozart}} recommended 55edo or something close to it, with a subset and further approximation used for keyboard instruments which (apart from an experimental instrument) did not have enough notes per octave to accommodate it in full.<ref>Chesnut, John (1977) ''Mozart's Teaching of Intonation'', '''Journal of the American Musicological Society''' Vol. 30, No. 2 (Summer, 1977), pp. 254-271 (Published By: University of California Press) [https://doi.org/10.2307/831219 doi.org/10.2307/831219], [http://www.jstor.org/stable/831219 https://www.jstor.org/stable/831219]</ref> It can also be used for [[Meantone family|mohajira and liese]] temperaments. It also supports an extremely sharp tuning of [[huygens|Huygens/undecimal meantone]] using the 55de [[val]], meaning that primes 7 and 11 are mapped very sharply to their second-best mapping.
55edo can be used for a [[meantone]] tuning, and is close to [[1/6-comma meantone]] (and is almost exactly 10/57-comma meantone). {{w|Georg Philipp Telemann|Telemann}} suggested it as a theoretical basis for analyzing the [[meantone intervals|intervals of meantone]]. {{w|Leopold Mozart|Leopold}} and {{w|Wolfgang Amadeus Mozart|Wolfgang Mozart}} recommended 55edo or something close to it, with a subset and further approximation used for keyboard instruments which (apart from an experimental instrument) did not have enough notes per octave to accommodate it in full.<ref>Chesnut, John (1977) ''Mozart's Teaching of Intonation'', '''Journal of the American Musicological Society''' Vol. 30, No. 2 (Summer, 1977), pp. 254-271 (Published By: University of California Press) [https://doi.org/10.2307/831219 doi.org/10.2307/831219], [http://www.jstor.org/stable/831219 https://www.jstor.org/stable/831219]</ref> It can also be used for [[Meantone_family#Mohajira|Mohajira]] and [[Meantone_family#Liese|Liese]] temperaments. It also supports an extremely sharp tuning of [[huygens|Huygens/undecimal meantone]] using the 55de [[val]], meaning that primes 7 and 11 are mapped very sharply to their second-best mapping.


=== Odd harmonics ===
=== Odd harmonics ===
Line 209: Line 209:
| 26
| 26
| 567.3
| 567.3
| 18/13
| [[7/5]], [[18/13]]
| vA4
| vA4
| downaug 4th
| downaug 4th
Line 216: Line 216:
| 27
| 27
| 589.1
| 589.1
| 7/5, 24/17
| 24/17
| A4, vd5
| A4, vd5
| aug 4th, downdim 5th
| aug 4th, downdim 5th
Line 223: Line 223:
| 28
| 28
| 610.9
| 610.9
| 10/7, 17/12
| 17/12
| ^A4, d5
| ^A4, d5
| upaug 4th, dim 5th
| upaug 4th, dim 5th
Line 230: Line 230:
| 29
| 29
| 632.7
| 632.7
| 13/9
| [[10/7]], [[13/9]]
| ^d5
| ^d5
| updim 5th
| updim 5th
Line 418: Line 418:
|}
|}
<nowiki />* 55f val (tending flat), inconsistent intervals labeled in ''italic''
<nowiki />* 55f val (tending flat), inconsistent intervals labeled in ''italic''
== Notation ==
=== Ups and downs notation ===
55edo can be notated with [[ups and downs]], spoken as up, dup, downsharp, sharp, upsharp etc. and down, dud, upflat etc. Note that dup is equivalent to dudsharp and dud is equivalent to dupflat.
{{Sharpness-sharp4a}}
[[Alternative symbols for ups and downs notation]] uses sharps and flats with arrows, borrowed from extended [[Helmholtz–Ellis notation]]:
{{Sharpness-sharp4}}
=== Sagittal notation ===
==== Evo flavor ====
<imagemap>
File:55-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 615 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 160 106 [[896/891]]
rect 160 80 280 106 [[33/32]]
default [[File:55-EDO_Evo_Sagittal.svg]]
</imagemap>
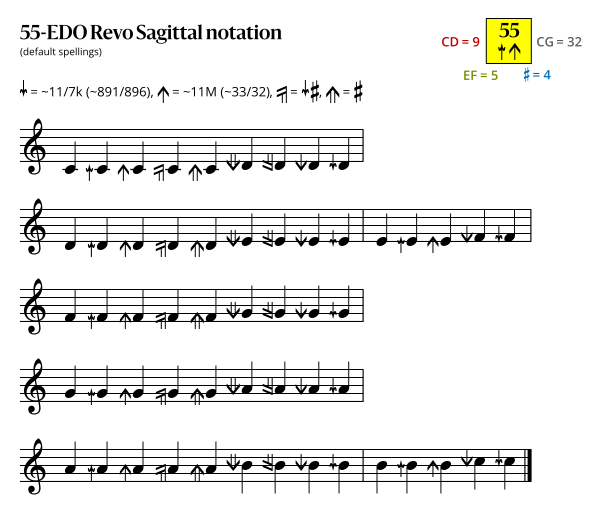
==== Revo flavor ====
<imagemap>
File:55-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 599 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 160 106 [[896/891]]
rect 160 80 280 106 [[33/32]]
default [[File:55-EDO_Revo_Sagittal.svg]]
</imagemap>
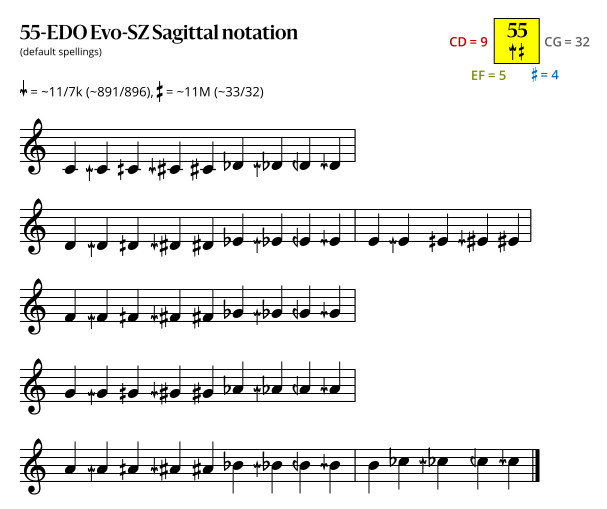
==== Evo-SZ flavor ====
<imagemap>
File:55-EDO_Evo-SZ_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 607 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 160 106 [[896/891]]
rect 160 80 280 106 [[33/32]]
default [[File:55-EDO_Evo-SZ_Sagittal.svg]]
</imagemap>
=== 31-tone subset ===
The 31-out-of-55edo subset can be notated entirely with the standard notation of 7 each of naturals/sharps/flats, and 5 each of doublesharps/doubleflats, as a 31-tone chain-of-5ths from Gbb to Ax.
[[File:Monzo55Notation.jpeg|400px|frameless|alt=Diagram of 31-tone subset of 55edo using plain Western notation, by Joe Monzo.|Diagram of 31-tone subset of 55edo using plain Western notation, by [[Joe Monzo]].]]


== Approximation to JI ==
== Approximation to JI ==
[[File:55ed2.svg|250px|thumb|right|alt=alt : Your browser has no SVG support.|Selected 19-limit intervals approximated in 55edo]]
[[File:55ed2.svg|250px|thumb|right|alt=alt : Your browser has no SVG support.|Selected 19-limit intervals approximated in 55edo]]
=== Selected just intervals by error ===
=== Selected just intervals by error ===
{{Q-odd-limit intervals|55}}
{{Q-odd-limit intervals|55}}
Line 447: Line 493:
| 81/80, {{monzo| 31 1 -14 }}
| 81/80, {{monzo| 31 1 -14 }}
| {{mapping| 55 87 128 }}
| {{mapping| 55 87 128 }}
| &minus;0.13
| −0.13
| 2.10
| 2.10
| 9.63
| 9.63
|}
|}
=== Uniform maps ===
{{Uniform map|edo=55}}


=== Commas ===
=== Commas ===
{{Todo|cleanup|inline=true}}
'''5-limit commas''': [[81/80]], [[Quintosec_family|{{monzo| 47 -15 -10 }}]], {{monzo| 31 1 -14 }}, {{monzo| 27 5 -15 }}
'''5-limit commas''': [[81/80]], [[Quintosec_family|{{monzo| 47 -15 -10 }}]], {{monzo| 31 1 -14 }}, {{monzo| 27 5 -15 }}


Line 476: Line 527:
| 14/13
| 14/13
| [[Twothirdtonic]] (55f)
| [[Twothirdtonic]] (55f)
|-
|1
|8\55
|174.5
|[[10/9]]~[[11/10]]
|[[Tetracot]] (55c)
|-
|-
| 1
| 1
Line 514: Line 571:
|}
|}
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if distinct
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if distinct
== Scales ==
; Subsets of twothirdtonic[37]
* Undecimal otonal-like pentatonic: 17 8 7 12 11
; Subsets of hendecatonic[33]
* Septimal pentatonic-like: 10 13 9 13 10
* Septimal minor blues-like: 13 10 4 5 13 10
* Septimal heptatonic blues-like: 13 10 4 5 8 5 10
; Others
* Sakura-like scale containing [[phi]]: 9 6 18 5 17
* Quasi-[[equiheptatonic]] scale: 8 8 7 9 7 9 7


== Instruments ==
== Instruments ==
Line 521: Line 591:
=== Modern renderings ===
=== Modern renderings ===
; {{W|Johann Sebastian Bach}}
; {{W|Johann Sebastian Bach}}
* [https://www.youtube.com/watch?v=oymJKnYzzOw "Jesus bleibet meine Freude" from ''Herz und Mund und Tat und Leben'', BWV 147] (1723) &ndash; arranged for two organs, rendered by Claudi Meneghin (2021)
* [https://www.youtube.com/watch?v=oymJKnYzzOw "Jesus bleibet meine Freude" from ''Herz und Mund und Tat und Leben'', BWV 147] (1723) – arranged for two organs, rendered by Claudi Meneghin (2021)
* [https://www.youtube.com/watch?v=Y5sIjh_Te40 "Contrapunctus 4" from ''The Art of Fugue'', BWV 1080] (1742&ndash;1749) &ndash; rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=xoCNOIsjfeU "Ricercar a 3" from ''The Musical Offering'', BWV 1079] (1747) – rendered by [[Claudi Meneghin]] (2024)
* [https://www.youtube.com/watch?v=QOPxqNgkVWM "Contrapunctus 11" from ''The Art of Fugue'', BWV 1080] (1742&ndash;1749) &ndash; rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=OkRVNo19guo "Ricercar a 6" from ''The Musical Offering'', BWV 1079] (1747) – rendered by Claudi Meneghin (2025)
* [https://www.youtube.com/watch?v=Y5sIjh_Te40 "Contrapunctus 4" from ''The Art of Fugue'', BWV 1080] (1742–1749) – rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=QOPxqNgkVWM "Contrapunctus 11" from ''The Art of Fugue'', BWV 1080] (1742–1749) – rendered by Claudi Meneghin (2024)


; {{W|Nicolaus Bruhns}}
; {{W|Nicolaus Bruhns}}
* [https://www.youtube.com/watch?v=OfOt3nOp-f8 ''Prelude in E Minor "The Great"''] &ndash; rendered by Claudi Meneghin (2023)
* [https://www.youtube.com/watch?v=OfOt3nOp-f8 ''Prelude in E Minor "The Great"''] – rendered by [[Claudi Meneghin]] (2023)
* [https://www.youtube.com/watch?v=tuIPIhSxUPs ''Prelude in E Minor "The Little"''] &ndash; rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=tuIPIhSxUPs ''Prelude in E Minor "The Little"''] – rendered by Claudi Meneghin (2024)
 
; {{W|Georg Frideric Handel}}
* [https://www.youtube.com/watch?v=rDvKPuzsno8 ''Fugue'' from "Suite in E minor", HWV 429] (1720) – arranged for Baroque ensemble and drums, rendered by Claudi Meneghin (2025)  


; {{W|Scott Joplin}}
; {{W|Scott Joplin}}
* [https://www.youtube.com/watch?v=GbhpuoIJgxk ''Maple Leaf Rag''] (1899) &ndash; arranged for harpsichord and rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=GbhpuoIJgxk ''Maple Leaf Rag''] (1899) – arranged for harpsichord and rendered by [[Claudi Meneghin]] (2024)


; {{W|Wolfgang Amadeus Mozart}}
; {{W|Wolfgang Amadeus Mozart}}
* [https://www.youtube.com/watch?v=C_AML6XW-2g ''Rondo alla Turca'' from the Piano Sonata No. 11, KV 331] (1778) &ndash; rendered by Francium (2023)
* [https://www.youtube.com/watch?v=C_AML6XW-2g ''Rondo alla Turca'' from the Piano Sonata No. 11, KV 331] (1778) – rendered by Francium (2023)
* [https://www.youtube.com/watch?v=XgRksdk6zyQ ''Fugue in G minor'', KV 401] (1782) &ndash; rendered by Francium (2023)
* [https://www.youtube.com/watch?v=XgRksdk6zyQ ''Fugue in G minor'', KV 401] (1782) – rendered by Francium (2023)
* [http://www.seraph.it/dep/int/AdagioKV540.mp3 ''Adagio in B minor'', KV 540] (1788) &ndash; rendered by Carlo Serafini (2011) ([http://www.seraph.it/blog_files/706c4662272db7703def4d57edfcb955-119.html blog entry])
* [http://www.seraph.it/dep/int/AdagioKV540.mp3 ''Adagio in B minor'', KV 540] (1788) – rendered by Carlo Serafini (2011) ([http://www.seraph.it/blog_files/706c4662272db7703def4d57edfcb955-119.html blog entry])
* [https://www.youtube.com/watch?v=pFjJCj2MBTM ''Allegro'' from the Piano Sonata No. 16, KV 545] (1788) &ndash; rendered by Francium (2023)
* [https://www.youtube.com/watch?v=pFjJCj2MBTM ''Allegro'' from the Piano Sonata No. 16, KV 545] (1788) – rendered by Francium (2023)
* [https://www.youtube.com/watch?v=p88MWgdio14&list=PLC6ZSKWKnVz0mOTLQkCUi9ydWGLpBP8gZ&index=2 ''Mozart's Gigue KV 574, Arranged for Fortepiano (55-edo)''] – rendered by [[Claudi Meneghin]] (2025)


; {{W|Keiichi Okabe}}
; {{W|Keiichi Okabe}}
* [https://www.youtube.com/watch?v=L24G4Y7tZgI ''Yuutsu no Yuutsu''] (2006) &ndash; rendered by MortisTheneRd (2024)
* [https://www.youtube.com/watch?v=L24G4Y7tZgI ''Yuutsu no Yuutsu''] (2006) – rendered by MortisTheneRd (2024)


=== 21st century ===
=== 21st century ===
; [[Bryan Deister]]
* [https://www.youtube.com/shorts/l62rb8ULCXs ''55edo improv''] (2025)
* [https://www.youtube.com/watch?v=kVmToKkZU88 ''Waltz in 55edo''] (2025)
; [[James Kukula]]
* ''[https://app.box.com/s/8hq89cb3rqqkrhvkxgvqtppa255kcqrq?fbclid=IwY2xjawISjSlleHRuA2FlbQIxMAABHcl5t8n_C7QUJqdEnwSaWBc5u3BpldmcAjhQQljsQIPl1qJ-zdCr9T8NMw_aem_Ez0m-Ls_ZqI0-c0Ld-28Yg 55edo Melted Syntonic]'' (2025)
; [[Budjarn Lambeth]]
* ''[https://www.youtube.com/watch?v=9c5MtrZFNhA Improvisation One in 55edo]'' (2025)
* ''[https://www.youtube.com/watch?v=ggFGUn1Ya2A Improvisation Two in 55edo]'' (2025)
; [[Claudi Meneghin]]
; [[Claudi Meneghin]]
* [https://www.youtube.com/watch?v=AgsJCTyxqiM ''Double Fugue on "We Wish You a Merry Christmas" for String Quartet''] (2020)
* [https://www.youtube.com/watch?v=AgsJCTyxqiM ''Double Fugue on "We Wish You a Merry Christmas" for String Quartet''] (2020)
Line 547: Line 634:
* [https://www.youtube.com/watch?v=hCUIx1RzvEk ''Chacony "Lament & Deception"'' for Two Violins and Cello] (2021), [https://www.youtube.com/watch?v=abJP4euMlsg for Baroque Wind Ensemble] (2023)
* [https://www.youtube.com/watch?v=hCUIx1RzvEk ''Chacony "Lament & Deception"'' for Two Violins and Cello] (2021), [https://www.youtube.com/watch?v=abJP4euMlsg for Baroque Wind Ensemble] (2023)
* [https://www.youtube.com/watch?v=9zfWeO0eJdA Fantasy "Almost a Fugue" on a Theme by Giuliani, for String Quartet] (2021)
* [https://www.youtube.com/watch?v=9zfWeO0eJdA Fantasy "Almost a Fugue" on a Theme by Giuliani, for String Quartet] (2021)
* [https://www.youtube.com/watch?v=jOiub14Cskw ''Double Fugue on "Old McDonald" + "Shave & a Haircut"''] (2024)


; [[Herman Miller]]
; [[Herman Miller]]
* ''[https://soundcloud.com/morphosyntax-1/road-trip-to-nowhere Road Trip to Nowhere]'' (2021)
* ''[https://soundcloud.com/morphosyntax-1/road-trip-to-nowhere Road Trip to Nowhere]'' (2021)
* ''[https://soundcloud.com/morphosyntax-1/migration Migration]'' (2025)


== External links ==
== External links ==
* [http://tonalsoft.com/monzo/55edo/55edo.aspx Mozart's tuning: 55-edo
* ''[http://tonalsoft.com/monzo/55edo/55edo.aspx Mozart's tuning: 55-edo and its close relative, 1/6-comma meantone]'' (containing another listening example) on [[Tonalsoft Encyclopedia]]
and its close relative, 1/6-comma meantone] (containing another listening example) on [[Tonalsoft Encyclopedia]]


== References ==
== References ==

Latest revision as of 10:46, 19 August 2025

← 54edo 55edo 56edo →
Prime factorization 5 × 11
Step size 21.8182 ¢ 
Fifth 32\55 (698.182 ¢)
Semitones (A1:m2) 4:5 (87.27 ¢ : 109.1 ¢)
Consistency limit 5
Distinct consistency limit 5

55 equal divisions of the octave (abbreviated 55edo or 55ed2), also called 55-tone equal temperament (55tet) or 55 equal temperament (55et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 55 equal parts of about 21.8 ¢ each. Each step represents a frequency ratio of 21/55, or the 55th root of 2.

Theory

55edo can be used for a meantone tuning, and is close to 1/6-comma meantone (and is almost exactly 10/57-comma meantone). Telemann suggested it as a theoretical basis for analyzing the intervals of meantone. Leopold and Wolfgang Mozart recommended 55edo or something close to it, with a subset and further approximation used for keyboard instruments which (apart from an experimental instrument) did not have enough notes per octave to accommodate it in full.[1] It can also be used for Mohajira and Liese temperaments. It also supports an extremely sharp tuning of Huygens/undecimal meantone using the 55de val, meaning that primes 7 and 11 are mapped very sharply to their second-best mapping.

Odd harmonics

Approximation of odd harmonics in 55edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) -3.77 +6.41 -8.83 -7.55 -5.86 +10.38 +2.64 +4.14 +7.94 +9.22 +4.45
Relative (%) -17.3 +29.4 -40.5 -34.6 -26.9 +47.6 +12.1 +19.0 +36.4 +42.3 +20.4
Steps
(reduced) 		87
(32) 		128
(18) 		154
(44) 		174
(9) 		190
(25) 		204
(39) 		215
(50) 		225
(5) 		234
(14) 		242
(22) 		249
(29)

Subsets and supersets

Since 55 factors into 5 × 11, 55edo contains 5edo and 11edo as its subsets.

Intervals

# Cents Approximate ratios Ups and downs notation
0 0.0 1/1 P1 perfect 1sn D
1 21.8 65/64, 78/77, 99/98, 128/125 ^1 up 1sn ^D
2 43.6 36/35, 64/63 ^^1 dup 1sn ^^D
3 65.5 28/27 vvm2 dudminor 2nd vvEb
4 87.3 21/20, 18/17, 25/24 vm2 downminor 2nd vEb
5 109.1 16/15, 17/16 m2 minor 2nd Eb
6 130.9 13/12, 14/13 ^m2 upminor 2nd ^Eb
7 152.7 12/11, 11/10 ~2 mid 2nd vvE
8 174.5 vM2 downmajor 2nd vE
9 196.4 9/8, 10/9 M2 major 2nd E
10 218.2 17/15 ^M2 upmajor 2nd ^E
11 240.0 8/7 ^^M2 dupmajor 2nd ^^E
12 261.8 7/6 vvm3 dudminor 3rd vvF
13 283.6 13/11 vm3 downminor 3rd vF
14 305.5 6/5 m3 minor 3rd F
15 327.3 ^m3 upminor 3rd ^F
16 349.1 11/9, 27/22 ~3 mid 3rd ^^F
17 370.9 26/21, 16/13 vM3 downmajor 3rd vF#
18 392.7 5/4 M3 major 3rd F#
19 414.5 14/11 ^M3 upmajor 3rd ^F#
20 436.4 9/7 ^^M3 dupmajor 3rd ^^F#
21 458.2 21/16 vv4 dud 4th vvG
22 480.0 v4 down 4th vG
23 501.8 4/3, 27/20 P4 perfect 4th G
24 523.6 ^4 up 4th ^G
25 545.5 11/8, 15/11 ~4 mid 4th ^^G
26 567.3 7/5, 18/13 vA4 downaug 4th vG#
27 589.1 24/17 A4, vd5 aug 4th, downdim 5th G#, vAb
28 610.9 17/12 ^A4, d5 upaug 4th, dim 5th ^G#, Ab
29 632.7 10/7, 13/9 ^d5 updim 5th ^Ab
30 654.5 16/11, 22/15 ~5 mid 5th vvA
31 676.4 v5 down 5th vA
32 698.2 3/2, 40/27 P5 perfect 5th A
33 720.0 ^5 up 5th ^A
34 741.8 32/21 ^^5 dup 5th ^^A
35 763.6 14/9 vvm6 dudminor 6th vvBb
36 785.5 11/7 vm6 downminor 6th vBb
37 807.3 8/5 m6 minor 6th Bb
38 829.1 21/13, 13/8 ^m6 upminor 6th ^Bb
39 850.9 18/11, 44/27 ~6 mid 6th vvB
40 872.7 vM6 downmajor 6th vB
41 894.5 5/3 M6 major 6th B
42 916.4 22/13 ^M6 upmajor 6th ^B
43 938.2 12/7 ^^M6 dupmajor 6th ^^B
44 960.0 7/4 vvm7 dudminor 7th vvC
45 981.8 30/17 vm7 downminor 7th vC
46 1003.6 16/9, 9/5 m7 minor 7th C
47 1025.5 ^m7 upminor 7th ^C
48 1047.3 11/6, 20/11 ~7 mid 7th ^^C
49 1069.1 13/7, 24/13 vM7 downmajor 7th vC#
50 1090.9 15/8, 32/17 M7 major 7th C#
51 1112.7 40/21, 17/9, 48/25 ^M7 upmajor 7th ^C#
52 1134.5 56/27 ^^M7 dupmajor 7th ^^C#
53 1156.4 35/18, 63/32 vv8 dud 8ve vvD
54 1178.2 128/65, 77/39, 196/99, 125/64 v8 down 8ve vD
55 1200.0 2/1 P8 perfect 8ve D

* 55f val (tending flat), inconsistent intervals labeled in italic

Notation

Ups and downs notation

55edo can be notated with ups and downs, spoken as up, dup, downsharp, sharp, upsharp etc. and down, dud, upflat etc. Note that dup is equivalent to dudsharp and dud is equivalent to dupflat.

Step offset 0 1 2 3 4 5 6 7 8 9
Sharp symbol               
Flat symbol
                

Alternative symbols for ups and downs notation uses sharps and flats with arrows, borrowed from extended Helmholtz–Ellis notation:

Step offset 0 1 2 3 4 5 6 7 8 9
Sharp symbol
 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
Flat symbol  
 		 
 
 
 
 		 

Sagittal notation

Evo flavor

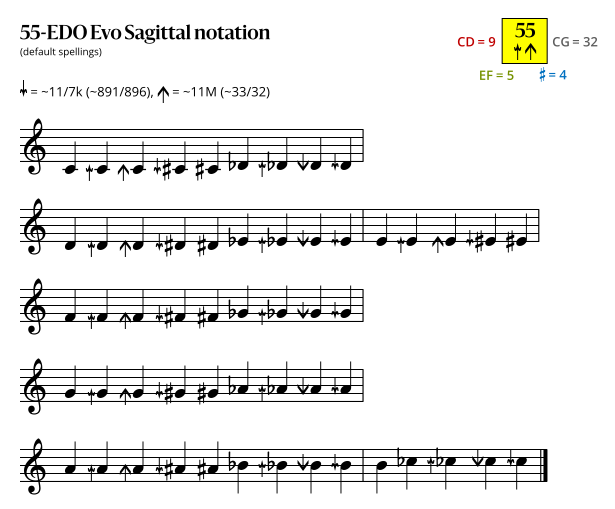
Sagittal notationPeriodic table of EDOs with sagittal notation896/89133/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation896/89133/32

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation896/89133/32

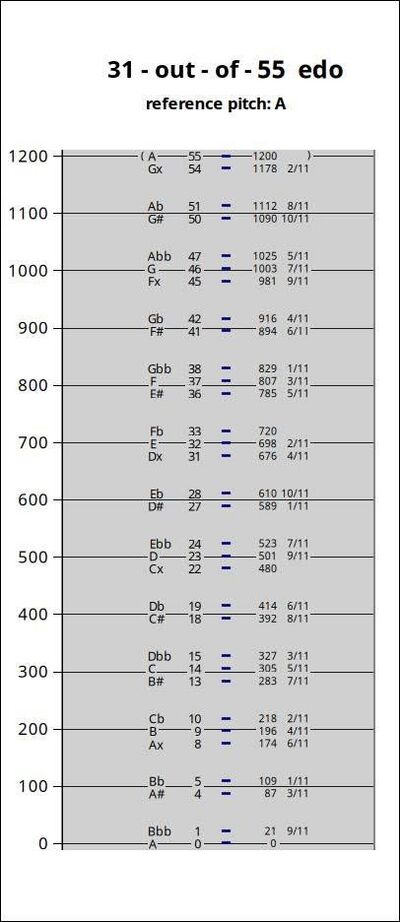
31-tone subset

The 31-out-of-55edo subset can be notated entirely with the standard notation of 7 each of naturals/sharps/flats, and 5 each of doublesharps/doubleflats, as a 31-tone chain-of-5ths from Gbb to Ax.

Diagram of 31-tone subset of 55edo using plain Western notation, by Joe Monzo.

Approximation to JI

alt : Your browser has no SVG support.
Selected 19-limit intervals approximated in 55edo

Selected just intervals by error

The following tables show how 15-odd-limit intervals are represented in 55edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 55edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
9/7, 14/9 1.280 5.9
11/9, 18/11 1.683 7.7
11/6, 12/11 2.090 9.6
13/7, 14/13 2.611 12.0
15/8, 16/15 2.640 12.1
11/7, 14/11 2.963 13.6
3/2, 4/3 3.773 17.3
13/9, 18/13 3.890 17.8
13/10, 20/13 3.968 18.2
7/6, 12/7 5.053 23.2
13/11, 22/13 5.573 25.5
11/8, 16/11 5.863 26.9
5/4, 8/5 6.414 29.4
7/5, 10/7 6.579 30.2
9/8, 16/9 7.546 34.6
13/12, 24/13 7.664 35.1
15/13, 26/15 7.741 35.5
9/5, 10/9 7.858 36.0
15/11, 22/15 8.504 39.0
7/4, 8/7 8.826 40.5
11/10, 20/11 9.541 43.7
5/3, 6/5 10.187 46.7
15/14, 28/15 10.352 47.4
13/8, 16/13 10.381 47.6
15-odd-limit intervals in 55edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
9/7, 14/9 1.280 5.9
11/9, 18/11 1.683 7.7
11/6, 12/11 2.090 9.6
15/8, 16/15 2.640 12.1
11/7, 14/11 2.963 13.6
3/2, 4/3 3.773 17.3
13/10, 20/13 3.968 18.2
7/6, 12/7 5.053 23.2
11/8, 16/11 5.863 26.9
5/4, 8/5 6.414 29.4
9/8, 16/9 7.546 34.6
15/13, 26/15 7.741 35.5
15/11, 22/15 8.504 39.0
7/4, 8/7 8.826 40.5
5/3, 6/5 10.187 46.7
13/8, 16/13 10.381 47.6
15/14, 28/15 11.466 52.6
11/10, 20/11 12.277 56.3
9/5, 10/9 13.960 64.0
13/12, 24/13 14.155 64.9
7/5, 10/7 15.239 69.8
13/11, 22/13 16.245 74.5
13/9, 18/13 17.928 82.2
13/7, 14/13 19.207 88.0
15-odd-limit intervals by 55d val mapping
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
11/9, 18/11 1.683 7.7
11/6, 12/11 2.090 9.6
13/7, 14/13 2.611 12.0
15/8, 16/15 2.640 12.1
3/2, 4/3 3.773 17.3
13/10, 20/13 3.968 18.2
11/8, 16/11 5.863 26.9
5/4, 8/5 6.414 29.4
7/5, 10/7 6.579 30.2
9/8, 16/9 7.546 34.6
15/13, 26/15 7.741 35.5
15/11, 22/15 8.504 39.0
5/3, 6/5 10.187 46.7
15/14, 28/15 10.352 47.4
13/8, 16/13 10.381 47.6
11/10, 20/11 12.277 56.3
7/4, 8/7 12.992 59.5
9/5, 10/9 13.960 64.0
13/12, 24/13 14.155 64.9
13/11, 22/13 16.245 74.5
7/6, 12/7 16.765 76.8
13/9, 18/13 17.928 82.2
11/7, 14/11 18.856 86.4
9/7, 14/9 20.539 94.1

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [-87 55⟩ [⟨55 87]] +1.31 1.19 7.21
2.3.5 81/80, [31 1 -14⟩ [⟨55 87 128]] −0.13 2.10 9.63

Uniform maps

13-limit uniform maps between 54.8 and 55.2
Min. size Max. size Wart notation Map
54.7778 54.9113 55cf ⟨55 87 127 154 190 203]
54.9113 54.9935 55f ⟨55 87 128 154 190 203]
54.9935 55.0340 55 ⟨55 87 128 154 190 204]
55.0340 55.0668 55d ⟨55 87 128 155 190 204]
55.0668 55.2064 55de ⟨55 87 128 155 191 204]

Commas

Todo: cleanup

5-limit commas: 81/80, [47 -15 -10⟩, [31 1 -14⟩, [27 5 -15⟩

7-limit commas: 31104/30625, 6144/6125, 81648/78125, 16128/15625, 28672/28125, 33075/32768, 83349/80000, 1029/1000, 686/675, 10976/10935, 16807/16384, 84035/82944

11-limit commas: 59049/58564, 74088/73205, 46656/46585, 21609/21296, 12005/11979, 19683/19360, 243/242, 3087/3025, 5488/5445, 19683/19250, 1944/1925, 45927/45056, 2835/2816, 35721/34375, 7056/6875, 12544/12375, 7203/7040, 2401/2376, 24057/24010, 72171/70000, 891/875, 176/175, 2079/2048, 385/384, 3234/3125, 17248/16875, 26411/25600, 26411/2592, 26411/262404, 88209/87808, 30976/30625, 3267/3200, 121/120, 81312/78125, 41503/40000, 41503/40500, 35937/35000, 2662/2625, 42592/42525, 83853/81920, 9317/9216, 65219/62500, 43923/43904, 14641/14400, 14641/14580

13-limit commas: 59535/57122, 29400/28561, 29568/28561, 29645/28561, 24576/24167, 99225/96668, 24500/24167, 50421/48334, 45927/43940, 2268/2197, 2240/2197, 57624/54925, 61875/61516, 57024/54925, 11264/10985, 72765/70304, 13475/13182, 22869/21970, 6776/6591, 20736/20449, 20480/20449, 84035/81796, 91125/91091, 65536/65065, 15309/14872, 1890/1859, 5600/5577, 9604/9295, 59049/57967, 58320/57967, 4374/4225, 864/845, 512/507, 11025/10816, 6125/6084, 21952/21125, 16807/16224, 84035/82134, 66825/66248, 90112/88725, 56133/54080, 693/676, 1540/1521, 26411/25350, 58806/57967, 58080/57967, 88209/84500, 4356/4225, 7744/7605, 88935/86528, 33275/33124, 27951/27040, 9317/9126, 58564/57967, 43923/42250, 17496/17303, 87808/86515, 55296/55055, 25515/25168, 1575/1573, 64827/62920, 4802/4719, 98415/98098, 59049/57200, 729/715, 144/143, 18375/18304, 18522/17875, 10976/10725, 84035/82368, 59049/56875, 11664/11375, 2304/2275, 4096/4095, 1701/1664, 105/104, 42336/40625, 25088/24375, 21609/20800, 2401/2340, 9604/9477, 72171/71344, 2673/2600, 66/65, 352/351, 13475/13312, 33957/32500, 15092/14625, 81675/81536, 58806/56875, 11616/11375, 61952/61425, 68607/66560, 847/832, 4235/4212, 35937/35672, 1331/1300, 5324/5265, 58564/56875, 85293/85184, 13377/13310, 85293/84700, 15288/15125, 31213/30976, 67392/67375, 28431/28160, 34944/34375, 4459/4400, 4459/4455, 28431/28000, 351/350, 79872/78125, 66339/65536, 51597/50000, 637/625, 10192/10125, 31213/30720, 31213/31104, 30888/30625, 1287/1280, 81081/78125, 16016/15625, 49049/48000, 49049/48600, 14157/14000, 33033/32768, 77077/75000, 51909/51200, 17303/17280, 75712/75625, 8281/8250, 41067/40960, 31941/31250, 9464/9375, 57967/57600, 91091/90000, 61347/61250, 79092/78125

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 6\55 130.9 14/13 Twothirdtonic (55f)
1 8\55 174.5 10/9~11/10 Tetracot (55c)
1 16\55 349.1 11/9 Mohaha
1 23\55 501.8 4/3 Meantone (55d)
1 26\55 567.3 7/5 Liese (55)
1 27\55 589.1 45/32 Untriton (55d) / aufo (55)
5 17\55
(5\55) 		370.9
(109.1) 		99/80
(16/15) 		Quintosec
11 23\55
(3\55) 		501.8
(65.5) 		4/3
(36/35) 		Hendecatonic (55)

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

Subsets of twothirdtonic[37]
  • Undecimal otonal-like pentatonic: 17 8 7 12 11
Subsets of hendecatonic[33]
  • Septimal pentatonic-like: 10 13 9 13 10
  • Septimal minor blues-like: 13 10 4 5 13 10
  • Septimal heptatonic blues-like: 13 10 4 5 8 5 10
Others
  • Sakura-like scale containing phi: 9 6 18 5 17
  • Quasi-equiheptatonic scale: 8 8 7 9 7 9 7

Instruments

Music

Modern renderings

Johann Sebastian Bach
Nicolaus Bruhns
Georg Frideric Handel
Scott Joplin
Wolfgang Amadeus Mozart
Keiichi Okabe

21st century

Bryan Deister
James Kukula
Budjarn Lambeth
Claudi Meneghin
Herman Miller

External links

References

  1. ↑ Chesnut, John (1977) Mozart's Teaching of Intonation, Journal of the American Musicological Society Vol. 30, No. 2 (Summer, 1977), pp. 254-271 (Published By: University of California Press) doi.org/10.2307/831219, https://www.jstor.org/stable/831219
Retrieved from "https://en.xen.wiki/index.php?title=55edo&oldid=207528"