Sensi
Sensi is a rank-2 regular temperament in the 2.3.5.7.13 subgroup generated by an extremely sharp major third of between 440 and 446 ¢ which represents both 9/7 and 13/10, such that two of these thirds stack to a major sixth which approximates 5/3, which cannot occur in 12edo. This results in 91/90, 126/125, and 245/243 being tempered out, making it an extension of both sensipent and BPS.
Equal temperaments that support sensi include 19edo (generator 7\19; soft checkertonic), 27edo (generator 10\27; supersoft checkertonic), and 46edo (generator 17\46; L/s = 7/5, more optimized for sensi temperament). More obscure but significantly more accurate interpretations of its generator are given by sensible and especially sensipent's extension to the 2.3.5.31 subgroup.
See Sensipent family #Sensi for more technical data, and Sensi extensions for extensions of sensi that include the 11th harmonic.
Intervals
Interval chain
In the following table, odd harmonics and subharmonics 1–21 are in bold.
| # | Cents* | Approximate ratios** |
|---|---|---|
| 0 | 0.0 | 1/1 |
| 1 | 443.3 | 9/7, 13/10 |
| 2 | 886.6 | 5/3, 42/25 |
| 3 | 129.9 | 13/12, 14/13, 15/14, 27/25 |
| 4 | 573.3 | 7/5, 18/13, 25/18 |
| 5 | 1016.6 | 9/5 |
| 6 | 259.9 | 7/6, 15/13 |
| 7 | 703.2 | 3/2 |
| 8 | 1146.5 | 27/14, 35/18 |
| 9 | 389.8 | 5/4 |
| 10 | 833.2 | 13/8, 21/13 |
| 11 | 76.5 | 21/20, 25/24 |
| 12 | 519.8 | 27/20 |
| 13 | 963.1 | 7/4 |
| 14 | 206.4 | 9/8 |
| 15 | 649.7 | 35/24 (sensor 16/11, sensus 22/15) |
| 16 | 1093.1 | 15/8 (sensor 32/17, sensus 17/9) |
| 17 | 336.4 | 39/32 (sensus 17/14) |
| 18 | 779.7 | 25/16 |
| 19 | 23.0 | 49/48, 65/64, 81/80 |
| 20 | 466.3 | 21/16 |
* In 2.3.5.7.13 CTE tuning
** 2.3.5.7.13 ratio interpretations
In Sensi[8]
Sensi[8] is a mos scale with a 3L 5s pattern (or 5L 3s in extreme cases where the generator is larger than 450 ¢). See 3L 5s#Modes (resp. 5L 3s#Modes) to see which modes have which qualities for each interval size.
Sortable table of Sensi[8]'s major and minor intervals in various sensi tunings:
| Degree | Size in 19edo (soft) | Size in 27edo (supersoft) | Size in 46edo | Approximate ratios | # generators up |
|---|---|---|---|---|---|
| Unison | 0\19, 0.0 | 0\27, 0.0 | 0\46, 0.0 | 1/1 | 0 |
| Min. sen2nd | 2\19, 126.3 | 3\27, 133.3 | 5\46, 130.4 | 14/13 | +3 |
| Maj. sen2nd | 3\19, 189.5 | 4\27, 177.8 | 7\46, 182.6 | 10/9 | −5 |
| Min. sen3rd | 4\19, 252.6 | 6\27, 266.7 | 10\46, 260.9 | 7/6 | +6 |
| Maj. sen3rd | 5\19, 315.8 | 7\27, 311.1 | 12\46, 313.0 | 6/5 | −2 |
| Perf. sen4th | 7\19, 442.1 | 10\27, 444.4 | 17\46, 443.5 | 9/7, 13/10 | +1 |
| Aug. sen4th | 8\19, 505.3 | 11\27, 488.9 | 19\46, 495.7 | 4/3 | −7 |
| Min. sen5th | 9\19, 568.4 | 13\27, 577.8 | 22\46, 573.9 | 7/5, 18/13 | +4 |
| Maj. sen5th | 10\19, 631.6 | 14\27, 622.2 | 24\46, 626.1 | 10/7, 13/9 | −4 |
| Dim. sen6th | 11\19, 694.7 | 16\27, 711.1 | 27\46, 704.3 | 3/2 | +7 |
| Perf. sen6th | 12\19, 757.9 | 17\27, 755.6 | 20\46, 756.5 | 14/9, 20/13 | −1 |
| Min. sen7th | 14\19, 884.2 | 20\27, 888.9 | 34\46, 887.0 | 5/3 | +2 |
| Maj. sen7th | 15\19, 947.4 | 21\27, 933.3 | 36\46, 939.1 | 12/7 | −6 |
| Min. sen8th | 16\19, 1010.5 | 23\27, 1022.2 | 39\46, 1017.4 | 9/5 | +5 |
| Maj. sen8th | 17\19, 1073.7 | 24\27, 1066.7 | 41\46, 1069.6 | 13/7 | −3 |
Chords
The "fundamental" otonal consonance of sensi (in this article's definition of sensi) is 4:5:6:7:9:13. However, the full chord isn't available in the 8-note MOS.
One of the most common consonant triads in sensi is the 6:10:13 triad, which spans 3 generators. Sensi[8] has five 6:10:13 triads, four 7:9:13 triads, three 5:6:7:9 tetrads and one 5:6:7:9:13 pentad. Having many diminished triads, it is similar to the 12edo diminished scale in some ways. Sensi is interesting mainly because it gives new 13-limit interpretations to fairly familiar (in the sense of extended meantone-like) intervals. Restricted to the 8-note MOS, it is essentially a non-over-1 temperament.
Melodically, sensi[8] sounds fairly familiar because many intervals are either 5-limit or have familiar categorical interpretations, being represented in the meantone tuning 19edo. For example, the small step of about 130 ¢ categorizes pretty well as a large semitone (except at places in the scale where two of them make a flat subminor third); the large step is a small whole tone representing 10/9.
The root-sen5th-sen8th chords in sensi[8] usually spell 5:7:9 (root-minor sen5th-minor sen8th) and 7:10:13 (root-major sen5th-major sen8th) chords (shown in the Anti-Dylathian mode QJKLMNOPQ = ssLssLsL):
- Q M P = ssLs sLs L ≈ 5:7:9
- J N Q = sLss LsL s is the odd one out
- K O J = LssL sLs s ≈ 7:10:13
- L P K = ssLs Lss L ≈ 5:7:9
- M Q L = sLsL ssL s ≈ 7:10:13
- N J M = LsLs sLs s ≈ 7:10:13
- O K N = sLss Lss L ≈ 5:7:9
- P L O = LssL ssL s ≈ 7:10:13
Other otonal chords approximated in the 8-note MOS include:
- Root – maj. sen7th – maj. sen8th ≈ 7:12:13
- Root – maj. sen2nd – maj. sen5th ≈ 9:10:13
- Root – min. sen3rd – dim. sen6th ≈ 6:7:9
- Root – perf. sen4th – dim. sen6th ≈ 10:13:15 (ultramajor triad)
- Root – perf. sen4th – maj. sen7th ≈ 7:9:13
- Root – perf. sen4th – maj. sen5th – maj. sen7th ≈ 7:9:10:13
- Root – perf. sen4th – min. sen7th ≈ 10:13:18
- Root – perf. sen4th – min. sen5th – min. sen7th ≈ 10:13:14:18
- Root – min. sen7th – min. sen3rd (+ octave) ≈ 3:5:7
- Root – min. sen7th – min. sen2nd (+ octave) ≈ 6:10:13
- Root – dim. sen6th – min. sen7th ≈ 6:9:10
- Root – dim. sen6th – min. sen2nd (+octave) ≈ 6:9:13
Scales
Tunings
Tuning spectrum
| Edo generators |
Unchanged interval (eigenmonzo)* |
Generator (¢) | Comments |
|---|---|---|---|
| 9/7 | 435.084 | ||
| 4\11 | 436.364 | 11cdf val | |
| 15/14 | 439.814 | ||
| 13/9 | 440.846 | ||
| 15/13 | 441.290 | ||
| 7\19 | 442.105 | Lower bound of 7- and 9-odd-limit, 2.3.5.7.13-subgroup 13-, 15-, and 21-odd-limit diamond monotone | |
| 5/3 | 442.179 | ||
| 13/7 | 442.766 | ||
| 5/4 | 442.924 | 5-odd-limit minimax | |
| 15/8 | 443.017 | ||
| 21/13 | 443.025 | ||
| 3/2 | 443.136 | 2.3.5.7.13-subgroup 15- and 21-odd-limit minimax | |
| 17\46 | 443.478 | ||
| 9/5 | 443.519 | 9-odd-limit and 2.3.5.7.13-subgroup 13-odd-limit minimax | |
| 21/16 | 443.539 | ||
| 7/4 | 443.756 | 7-odd-limit minimax | |
| 21/20 | 444.042 | ||
| 13/8 | 444.053 | ||
| 10\27 | 444.444 | Upper bound of 9-odd-limit, 2.3.5.7.13-subgroup 13-, 15-, and 21-odd-limit diamond monotone | |
| 7/6 | 444.478 | ||
| 117/70 | 444.649 | Exact geometric mean of 9/7 and 13/10 | |
| 7/5 | 445.628 | ||
| 13/12 | 446.191 | ||
| 3\8 | 450.000 | 8d val, upper bound of 7-odd-limit diamond monotone | |
| 13/10 | 454.214 |
* Besides the octave
Visualizations
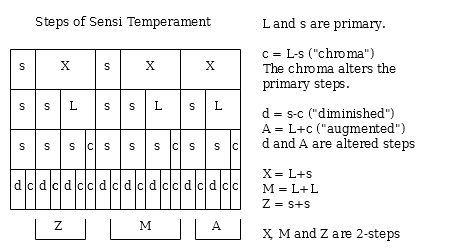
Steps of sensi
This diagram shows sensi[5], [8], [11], and [19] with intervals named in relation to the L and s of sensi[8].
Note that X, M and Z are not standard, but d and A are; they are short for "diminished" and "augmented".
Map of sensi
These diagrams relate the sensi generator chain (horizontal axis) to the steps within the octave (vertical axis) for sensi[8] and [11].
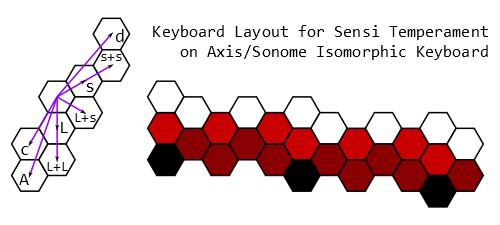
Isomorphic layout
This diagram shows a layout for playing sensi temperament on an isomorphic keyboard.
The darkest hexagons represent the same note (eg. C), but offset by octaves. The next-darkest hexagons show the notes of Sensi[5]. Imagine stepping from hex to hex as you move across the keyboard from left to right, landing only on the darkest and next-darkest hexes. The light red hexagons show additional notes needed to play Sensi[8]. The Large step of Sensi[8] is represented by a move straight down, so this pattern is a little more zig-zaggy than the pattern for Sensi[5]. Add the white hexes and you have Sensi[11]. The small step of Sensi[11] (indicated in the diagram as "c" for chroma), is represented by a move straight down and down-left. This pattern actually involves moving backward in the horizontal direction, and is therefore more zig-zaggy.
![map_of_sensi[8].png](/images/a/a6/Map_of_sensi-8-.png)
![map_of_sensi[11]_correction2.png](/images/9/97/Map_of_sensi-11-_correction2.png)
![sensi[19]in46.jpg](/images/f/f9/Sensi-19-in46.jpg)