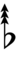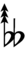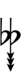47edo
| ← 46edo | 47edo | 48edo → |
(convergent)
47 equal divisions of the octave (abbreviated 47edo or 47ed2), also called 47-tone equal temperament (47tet) or 47 equal temperament (47et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 47 equal parts of about 25.5 ¢ each. Each step represents a frequency ratio of 21/47, or the 47th root of 2.
Theory
47edo is the first edo that has two diatonic perfect fifths, as both fall between 4\7 = 686 ¢ and 3\5 = 720 ¢. The fifth closest to 3/2 is 12.593-cent flat, unless you use the alternative fifth which is 12.939-cent sharp, similar to 35edo. The soft diatonic scale generated from its flat fifth is so soft, with L:s = 7:6, that it stops sounding like meantone or even a flattone system like 26edo or 40edo, but just sounds like a circulating temperament of 7edo. The hard diatonic scale generated from its sharp fifth is extremely hard, with L:s = 9:1. It has therefore not aroused much interest, but its best approximation to 9/8 is actually quite good, one-third-of-a-cent sharp.
47edo is one of the most difficult diatonic edos to notate in native fifths, because no other diatonic edo's fifth is as extreme.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -12.6 | -3.3 | +1.4 | +0.3 | +10.4 | +2.0 | +9.6 | -2.8 | +8.9 | -11.2 | +10.0 |
| Relative (%) | -49.3 | -13.1 | +5.4 | +1.4 | +40.7 | +7.9 | +37.6 | -11.1 | +34.7 | -43.9 | +39.3 | |
| Steps (reduced) |
74 (27) |
109 (15) |
132 (38) |
149 (8) |
163 (22) |
174 (33) |
184 (43) |
192 (4) |
200 (12) |
206 (18) |
213 (25) | |
47edo does a good job of approximating the 2.9.5.7.33.13.17.57.69 23-limit 2*47 subgroup of the 23-limit, on which it tempers out the same commas as 94edo. It provides a good tuning for baldy and silver and their relatives. It also provides a good tuning for the baseball temperament.
47edo can be treated as a dual-fifth system in the 2.3+.3-.5.7.13 subgroup, or the 3+.3-.5.7.11+.11-.13 subgroup for those who aren’t intimidated by lots of basis elements. As a dual-fifth system, it really shines, as both of its fifths have low enough harmonic entropy to sound consonant to many listeners, giving two consonant intervals for the price of one.
Subsets and supersets
47edo is the 15th prime edo, following 43edo and preceding 53edo, so it does not contain any nontrivial subset edos, though it contains 47ed4. 94edo, which doubles it, corrects its approximations of harmonics 3 and 11 to near-just qualities.
Intervals
| # | Cents | Relative notation | Absolute notation | |
|---|---|---|---|---|
| 0 | 0.0 | perfect unison | P1 | D |
| 1 | 25.5 | aug 1sn | A1 | D# |
| 2 | 51.1 | double-aug 1sn | AA1 | Dx |
| 3 | 76.6 | triple-aug 1sn, triple-dim 2nd | A31, d32 | D#3, Eb4 |
| 4 | 102.1 | double-dim 2nd | dd2 | Eb3 |
| 5 | 127.7 | dim 2nd | d2 | Ebb |
| 6 | 153.2 | minor 2nd | m2 | Eb |
| 7 | 178.7 | major 2nd | M2 | E |
| 8 | 204.3 | aug 2nd | A2 | E# |
| 9 | 229.8 | double-aug 2nd | AA2 | Ex |
| 10 | 255.3 | triple-aug 2nd, triple-dim 3rd | A32, d33 | E#3, Fb3 |
| 11 | 280.9 | double-dim 3rd | dd3 | Fbb |
| 12 | 306.4 | dim 3rd | d3 | Fb |
| 13 | 331.9 | minor 3rd | m3 | F |
| 14 | 357.4 | major 3rd | M3 | F# |
| 15 | 383.0 | aug 3rd | A3 | Fx |
| 16 | 408.5 | double-aug 3rd | AA3 | F#3 |
| 17 | 434.0 | triple-aug 3rd, triple-dim 4th | A33, d34 | F#4, Gb3 |
| 18 | 459.6 | double-dim 4th | dd4 | Gbb |
| 19 | 485.1 | dim 4th | d4 | Gb |
| 20 | 510.6 | perfect 4th | P4 | G |
| 21 | 536.2 | aug 4th | A4 | G# |
| 22 | 561.7 | double-aug 4th | AA4 | Gx |
| 23 | 587.2 | triple-aug 4th | A34 | G#3 |
| 24 | 612.8 | triple-dim 5th | d35 | Ab3 |
| 25 | 638.3 | double-dim 5th | dd5 | Abb |
| 26 | 663.8 | dim 5th | d5 | Ab |
| 27 | 689.4 | perfect 5th | P5 | A |
| 28 | 714.9 | aug 5th | A5 | A# |
| 29 | 740.4 | double-aug 5th | AA5 | Ax |
| 30 | 766.0 | triple-aug 5th, triple-dim 6th | A35, d36 | A#3, Bb4 |
| 31 | 791.5 | double-dim 6th | dd6 | Bb3 |
| 32 | 817.0 | dim 6th | d6 | Bbb |
| 33 | 842.6 | minor 6th | m6 | Bb |
| 34 | 868.1 | major 6th | M6 | B |
| 35 | 893.6 | aug 6th | A6 | B# |
| 36 | 919.1 | double-aug 6th | AA6 | Bx |
| 37 | 944.7 | triple-aug 6th, triple-dim 7th | A36, d37 | B#3, Cb3 |
| 38 | 970.2 | double-dim 7th | dd7 | Cbb |
| 39 | 995.7 | dim 7th | d7 | Cb |
| 40 | 1021.3 | minor 7th | m7 | C |
| 41 | 1046.8 | major 7th | M7 | C# |
| 42 | 1072.3 | aug 7th | A7 | Cx |
| 43 | 1097.9 | double-aug 7th | AA7 | C#3 |
| 44 | 1123.4 | triple-aug 7th, triple-dim 8ve | A37, d38 | C#4, Db3 |
| 45 | 1148.9 | double-dim 8ve | dd8 | Dbb |
| 46 | 1174.5 | dim 8ve | d8 | Db |
| 47 | 1200.0 | perfect 8ve | P8 | D |
Notation
A notation using the best 5th has major and minor 2nds of 7 and 6 edosteps respectively, with the naturals creating a 7edo-like scale:
D * * * * * * E * * * * * F * * * * * * G * * * * * * A * * * * * * B * * * * * C * * * * * * D
D# is next to D. This notation requires triple, quadruple and in some keys, quintuple or more sharps and flats. For example, a 0-15-27-38 chord (an approximate 4:5:6:7) on the note three edosteps above D would be spelled either as D#3 - F#5 - A#3 - C# or as Eb4 - Gbb - Ab4 - Db6. This is an aug-three double-dim-seven chord, written D#3(A3)dd7 or Eb4(A3)dd7. It could also be called a sharp-three triple-flat-seven chord, written D#3(#3)b37 or Eb4(#3)b37.
Using the 2nd best 5th is even more awkward. The major 2nd is 9 edosteps and the minor is only one. The naturals create a 5edo-like scale, with two of the notes inflected by a comma-sized edostep:
D * * * * * * * * E F * * * * * * * * G * * * * * * * * A * * * * * * * * B C * * * * * * * * D
D# is next to E. This notation requires quadruple, quintuple, and even sextuple ups and downs, as well as single sharps and flats.
Ups and downs notation
Using Helmholtz–Ellis accidentals and the sharp fifth, 47edo can be notated using ups and downs:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|||||||||||||||||||
| Flat symbol |
With the flat fifth, notation is identical to standard notation:
| Step offset | −2 | −1 | 0 | +1 | +2 |
|---|---|---|---|---|---|
| Symbol | |
|
|
|
|
Sagittal notation
Best fifth notation
This notation uses the same sagittal sequence as 42b.

Second-best fifth notation
Evo and Revo flavors

Alternative Evo flavor

Evo-SZ flavor

Scales
- Negri in zeta-stretched 47edo
- Quasi-equal equiheptatonic (Dorian): 7 6 7 7 7 6 7
- Quasi-equiheptatonic minor pentatonic: 13 7 7 13 7
- Quasi-equal equiheptatonic (Mixolydian): 7 7 6 7 7 6 7
- Quasi-equal equipentatonic: 9 10 9 10 9
- Sabertooth hexatonic: 3 9 3 13 12 7 (this is the original/default tuning; designed for the "gold" and "platinum" timbres in Scale Workshop)
- Sabertooth pentatonic: 3 9 3 13 19 (this is the original/default tuning)
- Sabertooth neutral: 3 11 14 11 8 (this is the original/default tuning)
Instruments
Lumatone
Skip fretting
Skip fretting system 47 3 11 is a skip-fretting system for 47edo where strings are 11\47 and frets are 3\47. This is effectively 15.6666...-edo. All examples of this system on this page are for 5-string bass.
- Chords
Neutral-dominant 7th: 1 0 1 2 2