15edt: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
'''15EDT''' is the [[Edt|equal division of the third harmonic]] into 15 parts of 126.7970 [[cent|cents]] each, corresponding to 9.4639 [[edo]]. | |||
Lookalikes: [[19ed4]] | |||
=Intervals | ==Properties== | ||
15EDT has harmonics 5 and 13 closely in tune, but does not do so well for 7 and 11, which are quite sharp. It tempers out the comma |0 22 -15> in the 5-limit, which is tempered out by [[19edo]] but has an [[optimal patent val]] of [[303edo]]. As a 3.5.13 subgroup system, it tempers out 2197/2187 and 3159/3125. Using the patent val, it tempers out 375/343 and 6561/6125 in the 7-limit; 81/77, 125/121, and 363/343 in the 11-limit; 65/63, 169/165, 585/539, and 1287/1225 in the 13-limit; 51/49, 121/119, 125/119, 189/187, and 195/187 in the 17-limit (no-twos subgroup). 15EDT is related to the 2.3.5.13 subgroup temperament 19&123, which has[[category:macrotonal]] a mapping [<1 0 0 0|, <0 15 22 35|], where the generator, an approximate 27/25, has a POTE tuning of 126.773, very close to 15EDT. | |||
With the patent 4, it tempers out 36/35, 64/63, and 375/343 in the 3.4.5.7 subgroup; 45/44, 80/77, 81/77, and 363/343 in the 3.4.5.7.11 subgroup; 52/49, 65/63, 65/64, 143/140, and 169/165 in the 3.4.5.7.11.13 subgroup; 51/49, 52/51, 85/84, and 121/119 in the 3.4.5.7.11.13.17 subgroup. | |||
==Intervals== | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 15: | Line 18: | ||
| | 0 | | | 0 | ||
| | 0 | | | 0 | ||
| | <span style="color: #660000;">[[ | | | <span style="color: #660000;">[[1/1]]</span> | ||
|- | |- | ||
| | 1 | | | 1 | ||
| | 126.797 | | | 126.797 | ||
| | [[ | | | [[14/13]], [[15/14]], [[16/15]], 29/27 | ||
|- | |- | ||
| | 2 | | | 2 | ||
| | 253.594 | | | 253.594 | ||
| | [[ | | | [[15/13]] | ||
|- | |- | ||
| | 3 | | | 3 | ||
| | 380.391 | | | 380.391 | ||
| | <span style="color: #660000;">[[ | | | <span style="color: #660000;">[[5/4]]</span> | ||
|- | |- | ||
| | 4 | | | 4 | ||
| | 507.188 | | | 507.188 | ||
| | [[ | | | [[4/3]] | ||
|- | |- | ||
| | 5 | | | 5 | ||
| | 633.985 | | | 633.985 | ||
| | [[ | | | [[13/9]] | ||
|- | |- | ||
| | 6 | | | 6 | ||
| | 760.782 | | | 760.782 | ||
| | <span style="color: #660000;">[[ | | | <span style="color: #660000;">[[14/9]]</span> | ||
|- | |- | ||
| | 7 | | | 7 | ||
| | 887.579 | | | 887.579 | ||
| | [[ | | | [[5/3]] | ||
|- | |- | ||
| | 8 | | | 8 | ||
| | 1014.376 | | | 1014.376 | ||
| | [[ | | | [[9/5]] | ||
|- | |- | ||
| | 9 | | | 9 | ||
| | 1141.173 | | | 1141.173 | ||
| | <span style="color: #660000;">[[ | | | <span style="color: #660000;">[[27/14]]</span> | ||
|- | |- | ||
| | 10 | | | 10 | ||
| | 1267.970 | | | 1267.970 | ||
| | [[27/ | | | [[27/26|27/13]] | ||
|- | |- | ||
| | 11 | | | 11 | ||
| | 1394.767 | | | 1394.767 | ||
| | [[ | | | [[9/4]] ([[9/8]] plus an octave) | ||
|- | |- | ||
| | 12 | | | 12 | ||
| | 1521.564 | | | 1521.564 | ||
| | [[ | | | [[12/5]] (<span style="color: #660000;">[[6/5]]</span> plus an octave) | ||
|- | |- | ||
| | 13 | | | 13 | ||
| | 1648.361 | | | 1648.361 | ||
| | [[ | | | [[13/5]] ([[13/10]] plus an octave) | ||
|- | |- | ||
| | 14 | | | 14 | ||
| | 1775.158 | | | 1775.158 | ||
| | [[ | | | [[14/5]] ([[7/5]] plus an octave) | ||
|- | |- | ||
| | 15 | | | 15 | ||
| | 1901.955 | | | 1901.955 | ||
| | [[ | | | [[3/1]] | ||
|} | |} | ||
15edt contains 4 intervals from [[ | 15edt contains 4 intervals from [[5edt]] and 2 intervals from [[3edt]], meaning that it contains 6 redundant intervals and 8 new intervals. The new intervals introduced include good approximations to 15/14, 15/13, 4/3, 5/3 and their tritave inverses. This allows for new chord possibilities such as 1:3:4:5:9:12:13:14:15:16... | ||
15edt also contains a 5L5s MOS similar to Blackwood Decatonic, which I call Ebony. This MOS has a period of 1/5 of the tritave and the generator is a single step. The major scale is sLsLsLsLsL, and the minor scale is LsLsLsLsLs. | 15edt also contains a 5L5s MOS similar to Blackwood Decatonic, which I call Ebony. This MOS has a period of 1/5 of the tritave and the generator is a single step. The major scale is sLsLsLsLsL, and the minor scale is LsLsLsLsLs. | ||
| Line 84: | Line 87: | ||
15edt approximates the 5th and 13th harmonics (and 29th) very well. Taking these as consonances one obtains an 3L+3s MOS "augmented scale", in which three 13/9 intervals close to a tritave, and another three are set 5/3 away. | 15edt approximates the 5th and 13th harmonics (and 29th) very well. Taking these as consonances one obtains an 3L+3s MOS "augmented scale", in which three 13/9 intervals close to a tritave, and another three are set 5/3 away. | ||
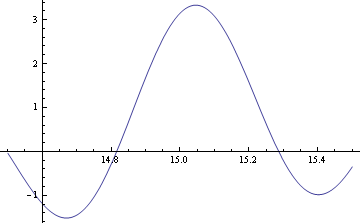
=Z function= | ==Z function== | ||
Below is a plot of the [[The_Riemann_Zeta_Function_and_Tuning#Removing primes|no-twos Z function]] in the vicinity of 15edt: | Below is a plot of the [[The_Riemann_Zeta_Function_and_Tuning#Removing primes|no-twos Z function]] in the vicinity of 15edt: | ||
| Line 92: | Line 95: | ||
[http://www.youtube.com/watch?v=bC_Pc4jKm2k http://www.youtube.com/watch?v=bC_Pc4jKm2k] | [http://www.youtube.com/watch?v=bC_Pc4jKm2k http://www.youtube.com/watch?v=bC_Pc4jKm2k] | ||
[[Category:Edt]] | |||
[[Category:Edonoi]] | |||
Revision as of 11:18, 15 February 2019
15EDT is the equal division of the third harmonic into 15 parts of 126.7970 cents each, corresponding to 9.4639 edo.
Lookalikes: 19ed4
Properties
15EDT has harmonics 5 and 13 closely in tune, but does not do so well for 7 and 11, which are quite sharp. It tempers out the comma |0 22 -15> in the 5-limit, which is tempered out by 19edo but has an optimal patent val of 303edo. As a 3.5.13 subgroup system, it tempers out 2197/2187 and 3159/3125. Using the patent val, it tempers out 375/343 and 6561/6125 in the 7-limit; 81/77, 125/121, and 363/343 in the 11-limit; 65/63, 169/165, 585/539, and 1287/1225 in the 13-limit; 51/49, 121/119, 125/119, 189/187, and 195/187 in the 17-limit (no-twos subgroup). 15EDT is related to the 2.3.5.13 subgroup temperament 19&123, which has a mapping [<1 0 0 0|, <0 15 22 35|], where the generator, an approximate 27/25, has a POTE tuning of 126.773, very close to 15EDT.
With the patent 4, it tempers out 36/35, 64/63, and 375/343 in the 3.4.5.7 subgroup; 45/44, 80/77, 81/77, and 363/343 in the 3.4.5.7.11 subgroup; 52/49, 65/63, 65/64, 143/140, and 169/165 in the 3.4.5.7.11.13 subgroup; 51/49, 52/51, 85/84, and 121/119 in the 3.4.5.7.11.13.17 subgroup.
Intervals
| Degrees | Cents | Approximate Ratios |
| 0 | 0 | 1/1 |
| 1 | 126.797 | 14/13, 15/14, 16/15, 29/27 |
| 2 | 253.594 | 15/13 |
| 3 | 380.391 | 5/4 |
| 4 | 507.188 | 4/3 |
| 5 | 633.985 | 13/9 |
| 6 | 760.782 | 14/9 |
| 7 | 887.579 | 5/3 |
| 8 | 1014.376 | 9/5 |
| 9 | 1141.173 | 27/14 |
| 10 | 1267.970 | 27/13 |
| 11 | 1394.767 | 9/4 (9/8 plus an octave) |
| 12 | 1521.564 | 12/5 (6/5 plus an octave) |
| 13 | 1648.361 | 13/5 (13/10 plus an octave) |
| 14 | 1775.158 | 14/5 (7/5 plus an octave) |
| 15 | 1901.955 | 3/1 |
15edt contains 4 intervals from 5edt and 2 intervals from 3edt, meaning that it contains 6 redundant intervals and 8 new intervals. The new intervals introduced include good approximations to 15/14, 15/13, 4/3, 5/3 and their tritave inverses. This allows for new chord possibilities such as 1:3:4:5:9:12:13:14:15:16...
15edt also contains a 5L5s MOS similar to Blackwood Decatonic, which I call Ebony. This MOS has a period of 1/5 of the tritave and the generator is a single step. The major scale is sLsLsLsLsL, and the minor scale is LsLsLsLsLs.
15edt approximates the 5th and 13th harmonics (and 29th) very well. Taking these as consonances one obtains an 3L+3s MOS "augmented scale", in which three 13/9 intervals close to a tritave, and another three are set 5/3 away.
Z function
Below is a plot of the no-twos Z function in the vicinity of 15edt:
Music: