7edo: Difference between revisions
m →Commas: +alternative names; -wrong ratio |
→Commas: +Prime limit column; chroma > dicot comma |
||
| Line 142: | Line 142: | ||
7 EDO tempers out the following commas. This assumes val {{val| 7 11 16 20 24 26 }}. | 7 EDO tempers out the following commas. This assumes val {{val| 7 11 16 20 24 26 }}. | ||
{| class="wikitable center- | {| class="wikitable center-1 center-2 right-4 center-5" | ||
|- | |- | ||
! [[Harmonic limit|Prime<br>Limit]] | |||
! [[Ratio]]s | ! [[Ratio]]s | ||
! [[Monzo]] | ! [[Monzo]] | ||
| Line 150: | Line 151: | ||
! Name(s) | ! Name(s) | ||
|- | |- | ||
| 3 | |||
| [[2187/2048]] | | [[2187/2048]] | ||
| {{Monzo| -11 7 }} | | {{Monzo| -11 7 }} | ||
| Line 156: | Line 158: | ||
| Apotome, Pythagorean chromatic semitone | | Apotome, Pythagorean chromatic semitone | ||
|- | |- | ||
| 5 | |||
| [[135/128]] | | [[135/128]] | ||
| {{Monzo| -7 3 1 }} | | {{Monzo| -7 3 1 }} | ||
| Line 162: | Line 165: | ||
| Major chroma, major limma, pelogic comma | | Major chroma, major limma, pelogic comma | ||
|- | |- | ||
| 5 | |||
| [[25/24]] | | [[25/24]] | ||
| {{Monzo| -3 -1 2 }} | | {{Monzo| -3 -1 2 }} | ||
| 70.67 | | 70.67 | ||
| Yoyo | | Yoyo | ||
| Classic chromatic semitone, | | Classic chromatic semitone, dicot comma | ||
|- | |- | ||
| 5 | |||
| [[250/243]] | | [[250/243]] | ||
| {{Monzo| 1 -5 3 }} | | {{Monzo| 1 -5 3 }} | ||
| Line 174: | Line 179: | ||
| Maximal diesis, porcupine comma | | Maximal diesis, porcupine comma | ||
|- | |- | ||
| 5 | |||
| [[20000/19683]] | | [[20000/19683]] | ||
| {{Monzo| 5 -9 4 }} | | {{Monzo| 5 -9 4 }} | ||
| Line 180: | Line 186: | ||
| Minimal diesis, tetracot comma | | Minimal diesis, tetracot comma | ||
|- | |- | ||
| 5 | |||
| [[81/80]] | | [[81/80]] | ||
| {{Monzo| -4 4 -1 }} | | {{Monzo| -4 4 -1 }} | ||
| Line 186: | Line 193: | ||
| Syntonic comma, Didymus comma, meantone comma | | Syntonic comma, Didymus comma, meantone comma | ||
|- | |- | ||
| 5 | |||
| [[1600000/1594323]] | | [[1600000/1594323]] | ||
| {{Monzo| 9 -13 5 }} | | {{Monzo| 9 -13 5 }} | ||
| Line 192: | Line 200: | ||
| Amity comma | | Amity comma | ||
|- | |- | ||
| 7 | |||
| [[36/35]] | | [[36/35]] | ||
| {{Monzo| 2 2 -1 -1 }} | | {{Monzo| 2 2 -1 -1 }} | ||
| Line 198: | Line 207: | ||
| Septimal quartertone | | Septimal quartertone | ||
|- | |- | ||
| 7 | |||
| [[525/512]] | | [[525/512]] | ||
| {{Monzo| -9 1 2 1 }} | | {{Monzo| -9 1 2 1 }} | ||
| Line 204: | Line 214: | ||
| Avicennma, Avicenna's enharmonic diesis | | Avicennma, Avicenna's enharmonic diesis | ||
|- | |- | ||
| 7 | |||
| [[64/63]] | | [[64/63]] | ||
| {{Monzo| 6 -2 0 -1 }} | | {{Monzo| 6 -2 0 -1 }} | ||
| Line 210: | Line 221: | ||
| Septimal comma, Archytas' comma, Leipziger Komma | | Septimal comma, Archytas' comma, Leipziger Komma | ||
|- | |- | ||
| 7 | |||
| [[875/864]] | | [[875/864]] | ||
| {{Monzo| -5 -3 3 1 }} | | {{Monzo| -5 -3 3 1 }} | ||
| Line 216: | Line 228: | ||
| Keema | | Keema | ||
|- | |- | ||
| 7 | |||
| [[5120/5103]] | | [[5120/5103]] | ||
| {{Monzo| 10 -6 1 -1 }} | | {{Monzo| 10 -6 1 -1 }} | ||
| Line 222: | Line 235: | ||
| Hemifamity | | Hemifamity | ||
|- | |- | ||
| 7 | |||
| [[6144/6125]] | | [[6144/6125]] | ||
| {{Monzo| 11 1 -3 -2 }} | | {{Monzo| 11 1 -3 -2 }} | ||
| Line 228: | Line 242: | ||
| Porwell | | Porwell | ||
|- | |- | ||
| 7 | |||
| [[4375/4374]] | | [[4375/4374]] | ||
| {{Monzo| -1 -7 4 1 }} | | {{Monzo| -1 -7 4 1 }} | ||
| Line 234: | Line 249: | ||
| Ragisma | | Ragisma | ||
|- | |- | ||
| 7 | |||
| … | | … | ||
| {{Monzo| 47 -7 -7 -7 }} | | {{Monzo| 47 -7 -7 -7 }} | ||
| Line 240: | Line 256: | ||
| Akjaysma, 5\7 octave comma | | Akjaysma, 5\7 octave comma | ||
|- | |- | ||
| 11 | |||
| [[100/99]] | | [[100/99]] | ||
| {{Monzo| 2 -2 2 0 -1 }} | | {{Monzo| 2 -2 2 0 -1 }} | ||
| Line 246: | Line 263: | ||
| Ptolemisma | | Ptolemisma | ||
|- | |- | ||
| 11 | |||
| [[121/120]] | | [[121/120]] | ||
| {{Monzo| -3 -1 -1 0 2 }} | | {{Monzo| -3 -1 -1 0 2 }} | ||
| Line 252: | Line 270: | ||
| Biyatisma | | Biyatisma | ||
|- | |- | ||
| 11 | |||
| [[176/175]] | | [[176/175]] | ||
| {{Monzo| 4 0 -2 -1 1 }} | | {{Monzo| 4 0 -2 -1 1 }} | ||
| Line 258: | Line 277: | ||
| Valinorsma | | Valinorsma | ||
|- | |- | ||
| 11 | |||
| [[65536/65219]] | | [[65536/65219]] | ||
| {{Monzo| 16 0 0 -2 -3 }} | | {{Monzo| 16 0 0 -2 -3 }} | ||
| Line 264: | Line 284: | ||
| Orgonisma | | Orgonisma | ||
|- | |- | ||
| 11 | |||
| [[243/242]] | | [[243/242]] | ||
| {{Monzo| -1 5 0 0 -2 }} | | {{Monzo| -1 5 0 0 -2 }} | ||
| Line 270: | Line 291: | ||
| Rastma | | Rastma | ||
|- | |- | ||
| 11 | |||
| [[385/384]] | | [[385/384]] | ||
| {{Monzo| -7 -1 1 1 1 }} | | {{Monzo| -7 -1 1 1 1 }} | ||
| Line 276: | Line 298: | ||
| Keenanisma | | Keenanisma | ||
|- | |- | ||
| 11 | |||
| [[4000/3993]] | | [[4000/3993]] | ||
| {{Monzo| 5 -1 3 0 -3 }} | | {{Monzo| 5 -1 3 0 -3 }} | ||
Revision as of 06:59, 20 December 2020
| ← 6edo | 7edo | 8edo → |
(semiconvergent)
7-edo or "Neutral diatonic" divides the 1200-cent octave into 7 equal parts, making its smallest interval 171.428¢, or the seventh root of 2. It is the fourth prime edo, after 2edo, 3edo and 5edo. It is the third zeta integral edo.
Theory
| prime 2 | prime 3 | prime 5 | prime 7 | prime 11 | prime 13 | ||
|---|---|---|---|---|---|---|---|
| error | absolute (¢) | 0.0 | -16.2 | -43.5 | +59.7 | -37.0 | +16.6 |
| relative (%) | 0 | -9 | -25 | +35 | -22 | +10 | |
| nearest edomapping | 7 | 4 | 2 | 6 | 3 | 5 | |
| fifthspan | 0 | +1 | -3 | -2 | -1 | +3 | |
Equal-heptatonic scales are used in non-western music in African cultures as well as an integral part of early Thai and early Chinese music. It has been speculated in "Indian music:history and structure", that the Indian three-sruti interval of 165 cents is close enough to be mistaken for 171 cents. (or 1.71 semitones).
7-tet can be thought of as result of stacking seven 11/9s on top of each other, and then tempering to remove the comma (2^-2 3^-14 11^7). As a temperament, William Lynch gives it the name "Neutron[7]" just as the whole tone scale of 12 ET is known as "Hexe[6]".
Typically, 7-edo exists as the tuning for pentatonic scales in traditional thai music with the other two pitches acting as auxiliary tones. However, it can be used as an interesting diatonic scale choice as well in tunings such as 14 EDO or 21 EDO.
The seventh of 7-edo is almost exactly the 29th harmonic (29/16), which can have a very agreeable sound with harmonic timbres. However it also finds itself nested between ratios such as 20/11 and 9/5, which gives it considerably higher harmonic entropy than 7/4, a much simpler overtone seventh.
Similarly, in equi-heptatonic systems the desire for harmonic sound may dictate constant adjustments of intonation away from the theoretical interval of 171 cents. One of the most impressive areas in Africa in which a pen-equidistant heptatonic scale is combined with a distinctively harmonic style based on singing in intervals of thirds plus fifths, or thirds plus fourths, is the eastern Angolan culture area. This music is heptatonic and non-modal; i.e., there is no concept of major or minor thirds as distinctive intervals. In principle all the thirds are neutral, but in practice the thirds rendered by the singers often approximate natural major thirds (386 cents), especially at points of rest. In this manner, the principles of equidistance and harmonic euphony are accommodated within one tonal-harmonic system. For the notation of such music, a seven-line stave is most appropriate, with each horizontal line representing one pitch level.
("African music." Encyclopædia Britannica. 2009. Encyclopædia Britannica Online. 05 Jul. 2009)
A Thai xylophone measured by Morton (1974) "varied only plus or minus 5 cents," from 7-TET. A Ugandan Chopi xylophone measured by Haddon (1952) was also tuned to this system.
Intervals
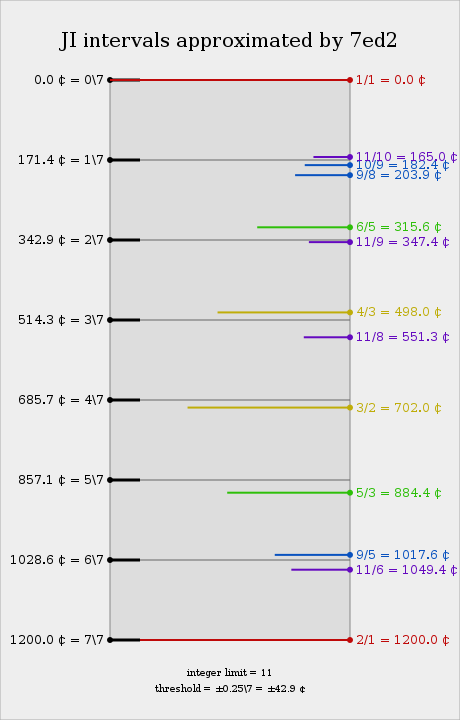
7edo can be notated on a five-line staff without accidentals. There is no distinction between Major or Minor; each pitch class is unique.
| Interval | Cents | interval name | The "neighborhood" of just intervals |
|---|---|---|---|
| 0 | 0.000 | unison / prime | exactly 1/1 |
| 1 | 171.429 | second | 6.424¢ from Ptolemy (neutral) second 11/10 3.215¢ from second 54/49 -1.006¢ from the 29th subharmonic 32/29 -10.975¢ from major second (small whole tone) 10/9 |
| 2 | 342.857 | third | 0.374¢ from neutral third 39/32
-4.55¢ from neutral third 11/9 |
| 3 | 514.286 | fourth | 16.241¢ from just fourth 4/3 (498.045¢) -5.265¢ from wide fourth 27/20 |
| 4 | 685.714 | fifth | 5.265 ¢ from narrow fifth 40/27 -16.241¢ from just fifth 3/2 (701.955¢) |
| 5 | 857.143 | sixth | 4.551¢ from neutral sixth 18/11
-0.374¢ from neutral sixth 64/39 |
| 6 | 1028.571 | seventh | 10.975¢ from (Didymus) minor seventh 9/5 -6.424¢ from neutral seventh 20/11 -1.006¢ from the 29th harmonic 29/16 -3.215¢ from seventh 49/27 |
| 7 | 1200 | octave | exactly 2/1 |
Observations
Related in a lateral way to traditional Thai music. Subset of 14 EDO and 21 EDO.
There is a neutral feel between whole tone scale and major/minor diatonic scale. The second (171.429 c) works well as a basic step for melodic progression.
The step from seventh to octave is too large for the leading tone.
Notation
William Lynch proposes using numbers 1 through 7 as the nominals of 7 ET with sharp signs being possible to expand to 14 EDO or even 21 EDO.
Commas
7 EDO tempers out the following commas. This assumes val ⟨7 11 16 20 24 26].
| Prime Limit |
Ratios | Monzo | Cents | Color Name | Name(s) |
|---|---|---|---|---|---|
| 3 | 2187/2048 | [-11 7⟩ | 113.69 | Lawa | Apotome, Pythagorean chromatic semitone |
| 5 | 135/128 | [-7 3 1⟩ | 92.18 | Layobi | Major chroma, major limma, pelogic comma |
| 5 | 25/24 | [-3 -1 2⟩ | 70.67 | Yoyo | Classic chromatic semitone, dicot comma |
| 5 | 250/243 | [1 -5 3⟩ | 49.17 | Triyo | Maximal diesis, porcupine comma |
| 5 | 20000/19683 | [5 -9 4⟩ | 27.66 | Saquadyo | Minimal diesis, tetracot comma |
| 5 | 81/80 | [-4 4 -1⟩ | 21.51 | Gu | Syntonic comma, Didymus comma, meantone comma |
| 5 | 1600000/1594323 | [9 -13 5⟩ | 6.15 | Saquinyo | Amity comma |
| 7 | 36/35 | [2 2 -1 -1⟩ | 48.77 | Rugu | Septimal quartertone |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma, Avicenna's enharmonic diesis |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal comma, Archytas' comma, Leipziger Komma |
| 7 | 875/864 | [-5 -3 3 1⟩ | 21.90 | Zotriyo | Keema |
| 7 | 5120/5103 | [10 -6 1 -1⟩ | 5.76 | Saruyo | Hemifamity |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.36 | Sarurutriyo | Porwell |
| 7 | 4375/4374 | [-1 -7 4 1⟩ | 0.40 | Zoquadyo | Ragisma |
| 7 | … | [47 -7 -7 -7⟩ | 0.34 | Trisa-rugu | Akjaysma, 5\7 octave comma |
| 11 | 100/99 | [2 -2 2 0 -1⟩ | 17.40 | Luyoyo | Ptolemisma |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lurugugu | Valinorsma |
| 11 | 65536/65219 | [16 0 0 -2 -3⟩ | 8.39 | Satrilu-aruru | Orgonisma |
| 11 | 243/242 | [-1 5 0 0 -2⟩ | 7.14 | Lulu | Rastma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 11 | 4000/3993 | [5 -1 3 0 -3⟩ | 3.03 | Triluyo | Wizardharry |
Music
- Death Giving Monolith by Stephen Weigel (dulcimer and voice)
- Jingle Bells cover! (recorded by Stephen Weigel)
- Pagan's Revenge by Bill Sethares (synthetic gamelan)
- I dream of Tibet [dead link] by Aaron K. Johnson (electronic swirlies) [dead link]
- Seven Equal Trio by Robert Walker ((synth) violin, viola, glockenspiel)
- Two-part Invention in 7TET by Aaron Hunt
- Pavouci, Kelt by Milan Guštar
- 7edo Dance by Carlo Serafini
- Nightfire (video) by Carlo Serafini (blog entry)
- Comets Over Flatland 6 by Randy Winchester
- Sävelmä [dead link] by Sävelmä (long version) by Juhani Nuorvala
- Rock in 7edo by Santiago Cosentino [dead link]
- Zhaleyka by Dmitry Bazhenov
Ear Training
7 EDO ear-training exercises by Alex Ness available here.