|
|
| Line 1: |
Line 1: |
| <h2>IMPORTED REVISION FROM WIKISPACES</h2>
| | __FORCETOC__ |
| This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
| | ----- |
| : This revision was by author [[User:TallKite|TallKite]] and made on <tt>2017-11-11 21:21:07 UTC</tt>.<br>
| | 72-tone equal temperament (or 72-edo) divides the octave into 72 steps or ''moria''. This produces a twelfth-tone tuning, with the whole tone measuring 200 cents, the same as in 12-tone equal temperament. 72-tone is also a superset of [[24edo|24-tone equal temperament]], a common and standard tuning of [[Arabic,_Turkish,_Persian|Arabic]] music, and has itself been used to tune Turkish music. |
| : The original revision id was <tt>621464699</tt>.<br>
| |
| : The revision comment was: <tt></tt><br>
| |
| The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
| |
| <h4>Original Wikitext content:</h4>
| |
| <div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">[[toc|flat]]
| |
| ---- | |
| 72-tone equal temperament (or 72-edo) divides the octave into 72 steps or //moria//. This produces a twelfth-tone tuning, with the whole tone measuring 200 cents, the same as in 12-tone equal temperament. 72-tone is also a superset of [[xenharmonic/24edo|24-tone equal temperament]], a common and standard tuning of [[xenharmonic/Arabic, Turkish, Persian|Arabic]] music, and has itself been used to tune Turkish music. | |
|
| |
|
| Composers that used 72-tone include Alois Hába, Ivan Wyschnegradsky, Julián Carillo (who is better associated with [[xenharmonic/96edo|96-edo]]), Iannis Xenakis, Ezra Sims, James Tenney and the jazz musician Joe Maneri. | | Composers that used 72-tone include Alois Hába, Ivan Wyschnegradsky, Julián Carillo (who is better associated with [[96edo|96-edo]]), Iannis Xenakis, Ezra Sims, James Tenney and the jazz musician Joe Maneri. |
|
| |
|
| 72-tone equal temperament approximates [[xenharmonic/11-limit|11-limit just intonation]] exceptionally well, is consistent in the [[xenharmonic/17-limit|17-limit]], and is the ninth [[xenharmonic/The Riemann Zeta Function and Tuning#Zeta%20EDO%20lists|Zeta integral tuning]]. The octave, fifth and fourth are the same size as they would be in 12-tone, 72, 42 and 30 steps respectively, but the major third (5/4) measures 23 steps, not 24, and other major intervals are one step flat of 12-et while minor ones are one step sharp. The septimal minor seventh (7/4) is 58 steps, while the undecimal semiaugmented fourth (11/8) is 33. | | 72-tone equal temperament approximates [[11-limit|11-limit just intonation]] exceptionally well, is consistent in the [[17-limit|17-limit]], and is the ninth [[The_Riemann_Zeta_Function_and_Tuning#Zeta EDO lists|Zeta integral tuning]]. The octave, fifth and fourth are the same size as they would be in 12-tone, 72, 42 and 30 steps respectively, but the major third (5/4) measures 23 steps, not 24, and other major intervals are one step flat of 12-et while minor ones are one step sharp. The septimal minor seventh (7/4) is 58 steps, while the undecimal semiaugmented fourth (11/8) is 33. |
|
| |
|
| 72 is an excellent tuning for [[xenharmonic/Gamelismic clan|miracle temperament]], especially the 11-limit version, and the related rank three temperament [[xenharmonic/Marvel family#Prodigy|prodigy]], and is a good tuning for other temperaments and scales, including wizard, harry, catakleismic, compton, unidec and tritikleismic. | | 72 is an excellent tuning for [[Gamelismic_clan|miracle temperament]], especially the 11-limit version, and the related rank three temperament [[Marvel_family#Prodigy|prodigy]], and is a good tuning for other temperaments and scales, including wizard, harry, catakleismic, compton, unidec and tritikleismic. |
|
| |
|
| =Commas= | | =Commas= |
|
| |
|
| Commas tempered out by 72edo include... | | Commas tempered out by 72edo include... |
|
| |
|
| ||~ 3-limit || | | {| class="wikitable" |
| || Pythagorean comma = 531441/524288 = |-19 12> || | | |- |
| | ! | 3-limit |
| | |- |
| | | | Pythagorean comma = 531441/524288 = |-19 12> |
| | |} |
| | |
| | {| class="wikitable" |
| | |- |
| | ! | 5-limit |
| | |- |
| | | | kleisma = 15625/15552 = |-6 -5 6> |
|
| |
|
| ||~ 5-limit ||
| |
| || kleisma = 15625/15552 = |-6 -5 6>
| |
| ampersand = 34171875/33554432 = |-25 7 6> | | ampersand = 34171875/33554432 = |-25 7 6> |
| | |
| graviton = 129140163/128000000 = |-13 17 -6> | | graviton = 129140163/128000000 = |-13 17 -6> |
| ennealimma = 7629394531250/7625597484987 = |1 -27 18> ||
| |
|
| |
|
| ||~ 7-limit ||~ 11-limit ||~ 13-limit || | | ennealimma = 7629394531250/7625597484987 = |1 -27 18> |
| || ............................... | | |} |
| | |
| | {| class="wikitable" |
| | |- |
| | ! | 7-limit |
| | ! | 11-limit |
| | ! | 13-limit |
| | |- |
| | | | ............................... |
| | |
| 225/224 | | 225/224 |
| | |
| 1029/1024 | | 1029/1024 |
| | |
| 2401/2400 | | 2401/2400 |
| | |
| 4375/4374 | | 4375/4374 |
| | |
| 16875/16807 | | 16875/16807 |
| | |
| 19683/19600 | | 19683/19600 |
| | |
| 420175/419904 | | 420175/419904 |
| 250047/250000 || ....................... | | |
| | 250047/250000 |
| | | | ....................... |
| | |
| 243/242 | | 243/242 |
| | |
| 385/384 | | 385/384 |
| | |
| 441/440 | | 441/440 |
| | |
| 540/539 | | 540/539 |
| | |
| 1375/1372 | | 1375/1372 |
| | |
| 3025/3024 | | 3025/3024 |
| | |
| 4000/3993 | | 4000/3993 |
| | |
| 6250/6237 | | 6250/6237 |
| 9801/9800 || ....................... | | |
| | 9801/9800 |
| | | | ....................... |
| | |
| 169/168 | | 169/168 |
| | |
| 325/324 | | 325/324 |
| | |
| 351/350 | | 351/350 |
| | |
| 364/363 | | 364/363 |
| | |
| 625/624 | | 625/624 |
| | |
| 676/675 | | 676/675 |
| | |
| 729/728 | | 729/728 |
| | |
| 1001/1000 | | 1001/1000 |
| | |
| 1575/1573 | | 1575/1573 |
| | |
| 1716/1715 | | 1716/1715 |
| | |
| 2080/2079 | | 2080/2079 |
| 6656/6655 ||
| |
|
| |
|
| =Temperaments= | | 6656/6655 |
| | |} |
| | |
| | =Temperaments= |
|
| |
|
| It provides the optimal patent val for miracle and wizard in the 7-limit, miracle, catakleismic, bikleismic, compton, ennealimnic, ennealiminal, enneaportent, marvolo and catalytic in the 11-limit, and catakleismic, bikleismic, compton, comptone, enneaportent, ennealim, catalytic, marvolo, manna, hendec, lizard, neominor, hours, and semimiracle in the 13-limit. | | It provides the optimal patent val for miracle and wizard in the 7-limit, miracle, catakleismic, bikleismic, compton, ennealimnic, ennealiminal, enneaportent, marvolo and catalytic in the 11-limit, and catakleismic, bikleismic, compton, comptone, enneaportent, ennealim, catalytic, marvolo, manna, hendec, lizard, neominor, hours, and semimiracle in the 13-limit. |
|
| |
|
| See also [[List of edo-distinct 72et rank two temperaments]]. | | See also [[List_of_edo-distinct_72et_rank_two_temperaments|List of edo-distinct 72et rank two temperaments]]. |
|
| |
|
| | =Harmonic Scale= |
| | Mode 8 of the harmonic series -- [[overtone_scales|overtones 8 through 16]], octave repeating -- is well-represented in 72edo. Note that all the different step sizes are distinguished, except for 13:12 and 14:13 (conflated to 8\72edo, 133.3 cents) and 15:14 and 16:15 (conflated to 7\72edo, 116.7 cents, the generator for miracle temperament). |
|
| |
|
| =Harmonic Scale= | | {| class="wikitable" |
| Mode 8 of the harmonic series -- [[xenharmonic/overtone scales|overtones 8 through 16]], octave repeating -- is well-represented in 72edo. Note that all the different step sizes are distinguished, except for 13:12 and 14:13 (conflated to 8\72edo, 133.3 cents) and 15:14 and 16:15 (conflated to 7\72edo, 116.7 cents, the generator for miracle temperament). | | |- |
| | | | Overtones in "Mode 8": |
| | | | 8 |
| | | | |
| | | | 9 |
| | | | |
| | | | 10 |
| | | | |
| | | | 11 |
| | | | |
| | | | 12 |
| | | | |
| | | | 13 |
| | | | |
| | | | 14 |
| | | | |
| | | | 15 |
| | | | |
| | | | 16 |
| | |- |
| | | | ...as JI Ratio from 1/1: |
| | | | 1/1 |
| | | | |
| | | | 9/8 |
| | | | |
| | | | 5/4 |
| | | | |
| | | | 11/8 |
| | | | |
| | | | 3/2 |
| | | | |
| | | | 13/8 |
| | | | |
| | | | 7/4 |
| | | | |
| | | | 15/8 |
| | | | |
| | | | 2/1 |
| | |- |
| | | | ...in cents: |
| | | | 0 |
| | | | |
| | | | 203.9 |
| | | | |
| | | | 386.3 |
| | | | |
| | | | 551.3 |
| | | | |
| | | | 702.0 |
| | | | |
| | | | 840.5 |
| | | | |
| | | | 968.8 |
| | | | |
| | | | 1088.3 |
| | | | |
| | | | 1200.0 |
| | |- |
| | | | Nearest degree of 72edo: |
| | | | 0 |
| | | | |
| | | | 12 |
| | | | |
| | | | 23 |
| | | | |
| | | | 33 |
| | | | |
| | | | 42 |
| | | | |
| | | | 50 |
| | | | |
| | | | 58 |
| | | | |
| | | | 65 |
| | | | |
| | | | 72 |
| | |- |
| | | | ...in cents: |
| | | | 0 |
| | | | |
| | | | 200.0 |
| | | | |
| | | | 383.3 |
| | | | |
| | | | 550.0 |
| | | | |
| | | | 700.0 |
| | | | |
| | | | 833.3 |
| | | | |
| | | | 966.7 |
| | | | |
| | | | 1083.3 |
| | | | |
| | | | 1200.0 |
| | |- |
| | | | Steps as Freq. Ratio: |
| | | | |
| | | | 9:8 |
| | | | |
| | | | 10:9 |
| | | | |
| | | | 11:10 |
| | | | |
| | | | 12:11 |
| | | | |
| | | | 13:12 |
| | | | |
| | | | 14:13 |
| | | | |
| | | | 15:14 |
| | | | |
| | | | 16:15 |
| | | | |
| | |- |
| | | | ...in cents: |
| | | | |
| | | | 203.9 |
| | | | |
| | | | 182.4 |
| | | | |
| | | | 165.0 |
| | | | |
| | | | 150.6 |
| | | | |
| | | | 138.6 |
| | | | |
| | | | 128.3 |
| | | | |
| | | | 119.4 |
| | | | |
| | | | 111.7 |
| | | | |
| | |- |
| | | | Nearest degree of 72edo: |
| | | | |
| | | | 12 |
| | | | |
| | | | 11 |
| | | | |
| | | | 10 |
| | | | |
| | | | 9 |
| | | | |
| | | | 8 |
| | | | |
| | | | 8 |
| | | | |
| | | | 7 |
| | | | |
| | | | 7 |
| | | | |
| | |- |
| | | | ...in cents: |
| | | | |
| | | | 200.0 |
| | | | |
| | | | 183.3 |
| | | | |
| | | | 166.7 |
| | | | |
| | | | 150.0 |
| | | | |
| | | | 133.3 |
| | | | |
| | | | 133.3 |
| | | | |
| | | | 116.7 |
| | | | |
| | | | 116.7 |
| | | | |
| | |} |
|
| |
|
| || Overtones in "Mode 8": || 8 || || 9 || || 10 || || 11 || || 12 || || 13 || || 14 || || 15 || || 16 ||
| | =Intervals= |
| || ...as JI Ratio from 1/1: || 1/1 || || 9/8 || || 5/4 || || 11/8 || || 3/2 || || 13/8 || || 7/4 || || 15/8 || || 2/1 ||
| |
| || ...in cents: || 0 || || 203.9 || || 386.3 || || 551.3 || || 702.0 || || 840.5 || || 968.8 || || 1088.3 || || 1200.0 ||
| |
| || Nearest degree of 72edo: || 0 || || 12 || || 23 || || 33 || || 42 || || 50 || || 58 || || 65 || || 72 ||
| |
| || ...in cents: || 0 || || 200.0 || || 383.3 || || 550.0 || || 700.0 || || 833.3 || || 966.7 || || 1083.3 || || 1200.0 ||
| |
| || Steps as Freq. Ratio: || || 9:8 || || 10:9 || || 11:10 || || 12:11 || || 13:12 || || 14:13 || || 15:14 || || 16:15 || ||
| |
| || ...in cents: || || 203.9 || || 182.4 || || 165.0 || || 150.6 || || 138.6 || || 128.3 || || 119.4 || || 111.7 || ||
| |
| || Nearest degree of 72edo: || || 12 || || 11 || || 10 || || 9 || || 8 || || 8 || || 7 || || 7 || ||
| |
| || ...in cents: || || 200.0 || || 183.3 || || 166.7 || || 150.0 || || 133.3 || || 133.3 || || 116.7 || || 116.7 || ||
| |
|
| |
|
| =Intervals= | | {| class="wikitable" |
| || degrees || cents value || approximate ratios (11-limit) ||||||= [[xenharmonic/Ups and Downs Notation|ups and downs ]][[xenharmonic/Ups and Downs Notation|notation]] || | | |- |
| || 0 || 0 || 1/1 ||= P1 ||= perfect unison ||= D || | | | | degrees |
| || 1 || 16.667 || 81/80 ||= ^1 ||= up unison ||= D^ || | | | | cents value |
| || 2 || 33.333 || 45/44 ||= ^^ ||= double-up unison ||= D^^ ||
| | | | approximate ratios (11-limit) |
| || 3 || 50 || 33/32 ||= ^<span style="font-size: 90%; vertical-align: super;">3</span>1, v<span style="font-size: 90%; vertical-align: super;">3</span>m2 ||= triple-up unison, | | | colspan="3" style="text-align:center;" | [[Ups_and_Downs_Notation|ups and downs ]][[Ups_and_Downs_Notation|notation]] |
| triple-down minor 2nd ||= D^<span style="font-size: 90%; vertical-align: super;">3</span>, Ebv<span style="font-size: 90%; vertical-align: super;">3</span> ||
| | |- |
| || 4 || 66.667 || 25/24 ||= vvm2 ||= double-downminor 2nd ||= Ebvv ||
| | | | 0 |
| || 5 || 83.333 || 21/20 ||= vm2 ||= downminor 2nd ||= Ebv ||
| | | | 0 |
| || 6 || 100 || 35/33 ||= m2 ||= minor 2nd ||= Eb || | | | | 1/1 |
| || 7 || 116.667 || 15/14 ||= ^m2 ||= upminor 2nd ||= Eb^ ||
| | | style="text-align:center;" | P1 |
| || 8 || 133.333 || 27/25 ||= v~2 ||= downmid 2nd ||= Eb^^ ||
| | | style="text-align:center;" | perfect unison |
| || 9 || 150 || 12/11 ||= ~2 ||= mid 2nd ||= Ev<span style="font-size: 90%; vertical-align: super;">3</span> ||
| | | style="text-align:center;" | D |
| || 10 || 166.667 || 11/10 ||= ^~2 ||= upmid 2nd ||= Evv ||
| | |- |
| || 11 || 183.333 || 10/9 ||= vM2 ||= downmajor 2nd ||= Ev ||
| | | | 1 |
| || 12 || 200 || 9/8 ||= M2 ||= major 2nd ||= E ||
| | | | 16.667 |
| || 13 || 216.667 || 25/22 ||= ^M2 ||= upmajor 2nd ||= E^ || | | | | 81/80 |
| || 14 || 233.333 || 8/7 ||= ^^M2 ||= double-upmajor 2nd ||= E^^ ||
| | | style="text-align:center;" | ^1 |
| || 15 || 250 || 81/70 ||= ^<span style="font-size: 90%; vertical-align: super;">3</span>M2, v<span style="font-size: 90%; vertical-align: super;">3</span>m3 ||= triple-up major 2nd, | | | style="text-align:center;" | up unison |
| triple-down minor 3rd ||= E^<span style="font-size: 90%; vertical-align: super;">3</span>, Fv<span style="font-size: 90%; vertical-align: super;">3</span> ||
| | | style="text-align:center;" | D^ |
| || 16 || 266.667 || 7/6 ||= vvm3 ||= double-downminor 3rd ||= Fvv || | | |- |
| || 17 || 283.333 || 33/28 ||= vm3 ||= downminor 3rd ||= Fv || | | | | 2 |
| || 18 || 300 || 25/21 ||= m3 ||= minor 3rd ||= F ||
| | | | 33.333 |
| || 19 || 316.667 || 6/5 ||= ^m3 ||= upminor 3rd ||= F^ ||
| | | | 45/44 |
| || 20 || 333.333 || 40/33 ||= v~3 ||= downmid 3rd ||= F^^ ||
| | | style="text-align:center;" | ^^ |
| || 21 || 350 || 11/9 ||= ~3 ||= mid 3rd ||= F^<span style="font-size: 90%; vertical-align: super;">3</span> || | | | style="text-align:center;" | double-up unison |
| || 22 || 366.667 || 99/80 ||= ^~3 ||= upmid 3rd ||= F#vv ||
| | | style="text-align:center;" | D^^ |
| || 23 || 383.333 || 5/4 ||= vM3 ||= downmajor 3rd ||= F#v ||
| | |- |
| || 24 || 400 || 44/35 ||= M3 ||= major 3rd ||= F# || | | | | 3 |
| || 25 || 416.667 || 14/11 ||= ^M3 ||= upmajor 3rd ||= F#^ ||
| | | | 50 |
| || 26 || 433.333 || 9/7 ||= ^^M3 ||= double-upmajor 3rd ||= F#^^ ||
| | | | 33/32 |
| || 27 || 450 || 35/27 ||= ^<span style="font-size: 90%; vertical-align: super;">3</span>M3, v<span style="font-size: 90%; vertical-align: super;">3</span>4 ||= triple-up major 3rd,
| | | style="text-align:center;" | ^<span style="font-size: 90%; vertical-align: super;">3</span>1, v<span style="font-size: 90%; vertical-align: super;">3</span>m2 |
| triple-down 4th ||= F#^<span style="font-size: 90%; vertical-align: super;">3</span>, Gv<span style="font-size: 90%; vertical-align: super;">3</span> ||
| | | style="text-align:center;" | triple-up unison, |
| || 28 || 466.667 || 21/16 ||= vv4 ||= double-down 4th ||= Gvv ||
| |
| || 29 || 483.333 || 33/25 ||= v4 ||= down 4th ||= Gv ||
| |
| || 30 || 500 || 4/3 ||= P4 ||= perfect 4th ||= G ||
| |
| || 31 || 516.667 || 27/20 ||= ^4 ||= up 4th ||= G^ ||
| |
| || 32 || 533.333 || 15/11 ||= ^^4 ||= double-up 4th ||= G^^ ||
| |
| || 33 || 550 || 11/8 ||= ^<span style="font-size: 90%; vertical-align: super;">3</span>4 ||= triple-up 4th ||= G^<span style="font-size: 90%; vertical-align: super;">3</span> ||
| |
| || 34 || 566.667 || 25/18 ||= vvA4 ||= double-down aug 4th ||= G#vv || | |
| || 35 || 583.333 || 7/5 ||= vA4, vd5 ||= downaug 4th, updim 5th ||= G#v, Abv ||
| |
| || 36 || 600 || 99/70 ||= A4, d5 ||= aug 4th, dim 5th ||= G#, Ab || | |
| || 37 || 616.667 || 10/7 ||= ^A4, ^d5 ||= upaug 4th, downdim 5th ||= G#^, Ab^ ||
| |
| || 38 || 633.333 || 36/25 ||= ^^d5 ||= double-updim 5th ||= Ab^^ ||
| |
| || 39 || 650 || 16/11 ||= v<span style="font-size: 90%; vertical-align: super;">3</span>5 ||= triple-down 5th ||= Av<span style="font-size: 90%; vertical-align: super;">3</span> ||
| |
| || 40 || 666.667 || 22/15 ||= vv5 ||= double-down 5th ||= Avv ||
| |
| || 41 || 683.333 || 40/27 ||= v5 ||= down 5th ||= Av ||
| |
| || 42 || 700 || 3/2 ||= P5 ||= perfect 5th ||= A ||
| |
| || 43 || 716.667 || 50/33 ||= ^5 ||= up 5th ||= A^ || | |
| || 44 || 733.333 || 32/21 ||= ^^5 ||= double-up 5th ||= A^^ ||
| |
| || 45 || 750 || 54/35 ||= ^<span style="font-size: 90%; vertical-align: super;">3</span>5, v<span style="font-size: 90%; vertical-align: super;">3</span>m6 ||= triple-up 5th, | |
| triple-down minor 6th ||= A^<span style="font-size: 90%; vertical-align: super;">3</span>, Bbv<span style="font-size: 90%; vertical-align: super;">3</span> ||
| |
| || 46 || 766.667 || 14/9 ||= vvm6 ||= double-downminor 6th ||= Bbvv ||
| |
| || 47 || 783.333 || 11/7 ||= vm6 ||= downminor 6th ||= Bbv ||
| |
| || 48 || 800 || 35/22 ||= m6 ||= minor 6th ||= Bb ||
| |
| || 49 || 816.667 || 8/5 ||= ^m6 ||= upminor 6th ||= Bb^ ||
| |
| || 50 || 833.333 || 81/50 ||= v~6 ||= downmid 6th ||= Bb^^ || | |
| || 51 || 850 || 18/11 ||= ~6 ||= mid 6th ||= Bv<span style="font-size: 90%; vertical-align: super;">3</span> ||
| |
| || 52 || 866.667 || 33/20 ||= ^~6 ||= upmid 6th ||= Bvv ||
| |
| || 53 || 883.333 || 5/3 ||= vM6 ||= downmajor 6th ||= Bv ||
| |
| || 54 || 900 || 27/16 ||= M6 ||= major 6th ||= B ||
| |
| || 55 || 916.667 || 56/33 ||= ^M6 ||= upmajor 6th ||= B^ ||
| |
| || 56 || 933.333 || 12/7 ||= ^^M6 ||= double-upmajor 6th ||= B^^ ||
| |
| || 57 || 950 || 121/70 ||= ^<span style="font-size: 90%; vertical-align: super;">3</span>M6, v<span style="font-size: 90%; vertical-align: super;">3</span>m7 ||= triple-up major 6th,
| |
| triple-down minor 7th ||= B^<span style="font-size: 90%; vertical-align: super;">3</span>, Cv<span style="font-size: 90%; vertical-align: super;">3</span> ||
| |
| || 58 || 966.667 || 7/4 ||= vvm7 ||= double-downminor 7th ||= Cvv ||
| |
| || 59 || 983.333 || 44/25 ||= vm7 ||= downminor 7th ||= Cv ||
| |
| || 60 || 1000 || 16/9 ||= m7 ||= minor 7th ||= C ||
| |
| || 61 || 1016.667 || 9/5 ||= ^m7 ||= upminor 7th ||= C^ ||
| |
| || 62 || 1033.333 || 20/11 ||= v~7 ||= downmid 7th ||= C^^ || | |
| || 63 || 1050 || 11/6 ||= ~7 ||= mid 7th ||= C^<span style="font-size: 90%; vertical-align: super;">3</span> || | |
| || 64 || 1066.667 || 50/27 ||= ^~7 ||= upmin 7th ||= C#vv ||
| |
| || 65 || 1083.333 || 15/8 ||= vM7 ||= downmajor 7th ||= C#v || | |
| || 66 || 1100 || 66/35 ||= M7 ||= major 7th ||= C# ||
| |
| || 67 || 1116.667 || 21/11 ||= ^M7 ||= upmajor 7th ||= C#^ ||
| |
| || 68 || 1133.333 || 27/14 ||= ^^M7 ||= double-upmajor 7th ||= C#^^ || | |
| || 69 || 1150 || 35/18 ||= ^<span style="font-size: 90%; vertical-align: super;">3</span>M7, v<span style="font-size: 90%; vertical-align: super;">3</span>8 ||= triple-up major 7th,
| |
| triple-down octave ||= C#^<span style="font-size: 90%; vertical-align: super;">3</span>, Dv<span style="font-size: 90%; vertical-align: super;">3</span> ||
| |
| || 70 || 1166.667 || 49/25 ||= vv8 ||= double-down octave ||= Dvv ||
| |
| || 71 || 1183.333 || 99/50 ||= v8 ||= down octave ||= Dv ||
| |
| || 72 || 1200 || 2/1 ||= P8 ||= perfect octave ||= D ||
| |
| Combining ups and downs notation with [[Kite's color notation|color notation]], qualities can be loosely associated with colors:
| |
| ||~ quality ||~ color ||~ monzo format ||~ examples ||
| |
| ||= double-down minor ||= blue ||= {a, b, 0, 1} ||= 7/6, 7/4 ||
| |
| ||= minor ||= fourthward white ||= {a, b}, b < -1 ||= 32/27, 16/9 ||
| |
| ||= upminor ||= green ||= {a, b, -1} ||= 6/5, 9/5 ||
| |
| ||= mid ||= jade ||= {a, b, 0, 0, 1} ||= 11/9, 11/6 ||
| |
| ||= " ||= amber ||= {a, b, 0, 0, -1} ||= 12/11, 18/11 ||
| |
| ||= downmajor ||= yellow ||= {a, b, 1} ||= 5/4, 5/3 ||
| |
| ||= major ||= fifthward white ||= {a, b}, b > 1 ||= 9/8, 27/16 || | |
| ||= double-up major ||= red ||= {a, b, 0, -1} ||= 9/7, 12/7 ||
| |
| All 72edo chords can be named using ups and downs. Here are the blue, green, jade, yellow and red triads:
| |
| ||~ color of the 3rd ||~ JI chord ||~ notes as edosteps ||~ notes of C chord ||~ written name ||~ spoken name ||
| |
| ||= blue ||= 6:7:9 ||= 0-16-42 ||= C Ebvv G ||= C.vvm ||= C double-down minor ||
| |
| ||= green ||= 10:12:15 ||= 0-19-42 ||= C Eb^ G ||= C.^m ||= C upminor ||
| |
| ||= jade ||= 18:22:27 ||= 0-21-42 ||= C Ev<span style="font-size: 90%; vertical-align: super;">3</span> G ||= C~ ||= C mid ||
| |
| ||= yellow ||= 4:5:6 ||= 0-23-42 ||= C Ev G ||= C.v ||= C downmajor or C dot down ||
| |
| ||= red ||= 14:18:27 ||= 0-26-42 ||= C E^^ G ||= C.^^ ||= C double-upmajor or C dot double-up ||
| |
| For a more complete list, see [[xenharmonic/Ups and Downs Notation#Chord%20names%20in%20other%20EDOs|Ups and Downs Notation - Chord names in other EDOs]].
| |
|
| |
|
| =Linear temperaments= | | triple-down minor 2nd |
| ||~ Periods per octave ||~ Generator ||~ Names || | | | style="text-align:center;" | D^<span style="font-size: 90%; vertical-align: super;">3</span>, Ebv<span style="font-size: 90%; vertical-align: super;">3</span> |
| || 1 || 1\72 || [[xenharmonic/quincy|quincy]] || | | |- |
| || 1 || 5\72 || [[marvolo]] ||
| | | | 4 |
| || 1 || 7\72 || [[xenharmonic/miracle|miracle]]/benediction/manna || | | | | 66.667 |
| || 1 || 11\72 || || | | | | 25/24 |
| || 1 || 13\72 || || | | | style="text-align:center;" | vvm2 |
| || 1 || 17\72 || [[xenharmonic/neominor|neominor]] || | | | style="text-align:center;" | double-downminor 2nd |
| || 1 || 19\72 || [[xenharmonic/catakleismic|catakleismic]] || | | | style="text-align:center;" | Ebvv |
| || 1 || 23\72 || || | | |- |
| || 1 || 25\72 || [[xenharmonic/sqrtphi|sqrtphi]] || | | | | 5 |
| || 1 || 29\72 || || | | | | 83.333 |
| || 1 || 31\72 || [[xenharmonic/marvo|marvo]]/zarvo || | | | | 21/20 |
| || 1 || 35\72 || [[xenharmonic/cotritone|cotritone]] || | | | style="text-align:center;" | vm2 |
| || 2 || 1\72 || || | | | style="text-align:center;" | downminor 2nd |
| || 2 || 5\72 || [[xenharmonic/harry|harry]] || | | | style="text-align:center;" | Ebv |
| || 2 || 7\72 || || | | |- |
| || 2 || 11\72 || [[xenharmonic/unidec|unidec]]/hendec || | | | | 6 |
| || 2 || 13\72 || [[xenharmonic/wizard|wizard]]/lizard/gizzard || | | | | 100 |
| || 2 || 17\72 || || | | | | 35/33 |
| || 3 || 1\72 || || | | | style="text-align:center;" | m2 |
| || 3 || 5\72 || [[xenharmonic/tritikleismic|tritikleismic]] || | | | style="text-align:center;" | minor 2nd |
| || 3 || 7\72 || || | | | style="text-align:center;" | Eb |
| || 3 || 11\72 || [[xenharmonic/mirkat|mirkat]] ||
| | |- |
| || 4 || 1\72 || [[xenharmonic/quadritikleismic|quadritikleismic]] || | | | | 7 |
| || 4 || 5\72 || || | | | | 116.667 |
| || 4 || 7\72 || || | | | | 15/14 |
| || 6 || 1\72 || || | | | style="text-align:center;" | ^m2 |
| || 6 || 5\72 || || | | | style="text-align:center;" | upminor 2nd |
| || 8 || 1\72 || [[xenharmonic/octoid|octoid]] || | | | style="text-align:center;" | Eb^ |
| || 8 || 2\72 || [[xenharmonic/octowerck|octowerck]] || | | |- |
| || 8 || 4\72 || || | | | | 8 |
| || 9 || 1\72 || || | | | | 133.333 |
| || 9 || 3\72 || [[xenharmonic/ennealimmal|ennealimmal]]/ennealimmic || | | | | 27/25 |
| || 12 || 1\72 || [[xenharmonic/compton|compton]] || | | | style="text-align:center;" | v~2 |
| || 18 || 1\72 || [[xenharmonic/hemiennealimmal|hemiennealimmal]] || | | | style="text-align:center;" | downmid 2nd |
| || 24 || 1\72 || [[xenharmonic/hours|hours]] || | | | style="text-align:center;" | Eb^^ |
| || 36 || 1\72 || || | | |- |
| | | | 9 |
| | | | 150 |
| | | | 12/11 |
| | | style="text-align:center;" | ~2 |
| | | style="text-align:center;" | mid 2nd |
| | | style="text-align:center;" | Ev<span style="font-size: 90%; vertical-align: super;">3</span> |
| | |- |
| | | | 10 |
| | | | 166.667 |
| | | | 11/10 |
| | | style="text-align:center;" | ^~2 |
| | | style="text-align:center;" | upmid 2nd |
| | | style="text-align:center;" | Evv |
| | |- |
| | | | 11 |
| | | | 183.333 |
| | | | 10/9 |
| | | style="text-align:center;" | vM2 |
| | | style="text-align:center;" | downmajor 2nd |
| | | style="text-align:center;" | Ev |
| | |- |
| | | | 12 |
| | | | 200 |
| | | | 9/8 |
| | | style="text-align:center;" | M2 |
| | | style="text-align:center;" | major 2nd |
| | | style="text-align:center;" | E |
| | |- |
| | | | 13 |
| | | | 216.667 |
| | | | 25/22 |
| | | style="text-align:center;" | ^M2 |
| | | style="text-align:center;" | upmajor 2nd |
| | | style="text-align:center;" | E^ |
| | |- |
| | | | 14 |
| | | | 233.333 |
| | | | 8/7 |
| | | style="text-align:center;" | ^^M2 |
| | | style="text-align:center;" | double-upmajor 2nd |
| | | style="text-align:center;" | E^^ |
| | |- |
| | | | 15 |
| | | | 250 |
| | | | 81/70 |
| | | style="text-align:center;" | ^<span style="font-size: 90%; vertical-align: super;">3</span>M2, v<span style="font-size: 90%; vertical-align: super;">3</span>m3 |
| | | style="text-align:center;" | triple-up major 2nd, |
|
| |
|
| =Z function= | | triple-down minor 3rd |
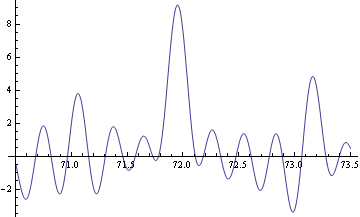
| 72edo is the ninth [[xenharmonic/The Riemann Zeta Function and Tuning#Zeta%20EDO%20lists|zeta integral edo]], as well as being a peak and gap edo, and the maximum value of the [[xenharmonic/The Riemann Zeta Function and Tuning#The%20Z%20function|Z function]] in the region near 72 occurs at 71.9506, giving an octave of 1200.824 cents, the stretched octaves of the zeta tuning. Below is a plot of Z in the region around 72.
| | | style="text-align:center;" | E^<span style="font-size: 90%; vertical-align: super;">3</span>, Fv<span style="font-size: 90%; vertical-align: super;">3</span> |
| | |- |
| | | | 16 |
| | | | 266.667 |
| | | | 7/6 |
| | | style="text-align:center;" | vvm3 |
| | | style="text-align:center;" | double-downminor 3rd |
| | | style="text-align:center;" | Fvv |
| | |- |
| | | | 17 |
| | | | 283.333 |
| | | | 33/28 |
| | | style="text-align:center;" | vm3 |
| | | style="text-align:center;" | downminor 3rd |
| | | style="text-align:center;" | Fv |
| | |- |
| | | | 18 |
| | | | 300 |
| | | | 25/21 |
| | | style="text-align:center;" | m3 |
| | | style="text-align:center;" | minor 3rd |
| | | style="text-align:center;" | F |
| | |- |
| | | | 19 |
| | | | 316.667 |
| | | | 6/5 |
| | | style="text-align:center;" | ^m3 |
| | | style="text-align:center;" | upminor 3rd |
| | | style="text-align:center;" | F^ |
| | |- |
| | | | 20 |
| | | | 333.333 |
| | | | 40/33 |
| | | style="text-align:center;" | v~3 |
| | | style="text-align:center;" | downmid 3rd |
| | | style="text-align:center;" | F^^ |
| | |- |
| | | | 21 |
| | | | 350 |
| | | | 11/9 |
| | | style="text-align:center;" | ~3 |
| | | style="text-align:center;" | mid 3rd |
| | | style="text-align:center;" | F^<span style="font-size: 90%; vertical-align: super;">3</span> |
| | |- |
| | | | 22 |
| | | | 366.667 |
| | | | 99/80 |
| | | style="text-align:center;" | ^~3 |
| | | style="text-align:center;" | upmid 3rd |
| | | style="text-align:center;" | F#vv |
| | |- |
| | | | 23 |
| | | | 383.333 |
| | | | 5/4 |
| | | style="text-align:center;" | vM3 |
| | | style="text-align:center;" | downmajor 3rd |
| | | style="text-align:center;" | F#v |
| | |- |
| | | | 24 |
| | | | 400 |
| | | | 44/35 |
| | | style="text-align:center;" | M3 |
| | | style="text-align:center;" | major 3rd |
| | | style="text-align:center;" | F# |
| | |- |
| | | | 25 |
| | | | 416.667 |
| | | | 14/11 |
| | | style="text-align:center;" | ^M3 |
| | | style="text-align:center;" | upmajor 3rd |
| | | style="text-align:center;" | F#^ |
| | |- |
| | | | 26 |
| | | | 433.333 |
| | | | 9/7 |
| | | style="text-align:center;" | ^^M3 |
| | | style="text-align:center;" | double-upmajor 3rd |
| | | style="text-align:center;" | F#^^ |
| | |- |
| | | | 27 |
| | | | 450 |
| | | | 35/27 |
| | | style="text-align:center;" | ^<span style="font-size: 90%; vertical-align: super;">3</span>M3, v<span style="font-size: 90%; vertical-align: super;">3</span>4 |
| | | style="text-align:center;" | triple-up major 3rd, |
|
| |
|
| [[image:xenharmonic/plot72.png]]
| | triple-down 4th |
| | | style="text-align:center;" | F#^<span style="font-size: 90%; vertical-align: super;">3</span>, Gv<span style="font-size: 90%; vertical-align: super;">3</span> |
| | |- |
| | | | 28 |
| | | | 466.667 |
| | | | 21/16 |
| | | style="text-align:center;" | vv4 |
| | | style="text-align:center;" | double-down 4th |
| | | style="text-align:center;" | Gvv |
| | |- |
| | | | 29 |
| | | | 483.333 |
| | | | 33/25 |
| | | style="text-align:center;" | v4 |
| | | style="text-align:center;" | down 4th |
| | | style="text-align:center;" | Gv |
| | |- |
| | | | 30 |
| | | | 500 |
| | | | 4/3 |
| | | style="text-align:center;" | P4 |
| | | style="text-align:center;" | perfect 4th |
| | | style="text-align:center;" | G |
| | |- |
| | | | 31 |
| | | | 516.667 |
| | | | 27/20 |
| | | style="text-align:center;" | ^4 |
| | | style="text-align:center;" | up 4th |
| | | style="text-align:center;" | G^ |
| | |- |
| | | | 32 |
| | | | 533.333 |
| | | | 15/11 |
| | | style="text-align:center;" | ^^4 |
| | | style="text-align:center;" | double-up 4th |
| | | style="text-align:center;" | G^^ |
| | |- |
| | | | 33 |
| | | | 550 |
| | | | 11/8 |
| | | style="text-align:center;" | ^<span style="font-size: 90%; vertical-align: super;">3</span>4 |
| | | style="text-align:center;" | triple-up 4th |
| | | style="text-align:center;" | G^<span style="font-size: 90%; vertical-align: super;">3</span> |
| | |- |
| | | | 34 |
| | | | 566.667 |
| | | | 25/18 |
| | | style="text-align:center;" | vvA4 |
| | | style="text-align:center;" | double-down aug 4th |
| | | style="text-align:center;" | G#vv |
| | |- |
| | | | 35 |
| | | | 583.333 |
| | | | 7/5 |
| | | style="text-align:center;" | vA4, vd5 |
| | | style="text-align:center;" | downaug 4th, updim 5th |
| | | style="text-align:center;" | G#v, Abv |
| | |- |
| | | | 36 |
| | | | 600 |
| | | | 99/70 |
| | | style="text-align:center;" | A4, d5 |
| | | style="text-align:center;" | aug 4th, dim 5th |
| | | style="text-align:center;" | G#, Ab |
| | |- |
| | | | 37 |
| | | | 616.667 |
| | | | 10/7 |
| | | style="text-align:center;" | ^A4, ^d5 |
| | | style="text-align:center;" | upaug 4th, downdim 5th |
| | | style="text-align:center;" | G#^, Ab^ |
| | |- |
| | | | 38 |
| | | | 633.333 |
| | | | 36/25 |
| | | style="text-align:center;" | ^^d5 |
| | | style="text-align:center;" | double-updim 5th |
| | | style="text-align:center;" | Ab^^ |
| | |- |
| | | | 39 |
| | | | 650 |
| | | | 16/11 |
| | | style="text-align:center;" | v<span style="font-size: 90%; vertical-align: super;">3</span>5 |
| | | style="text-align:center;" | triple-down 5th |
| | | style="text-align:center;" | Av<span style="font-size: 90%; vertical-align: super;">3</span> |
| | |- |
| | | | 40 |
| | | | 666.667 |
| | | | 22/15 |
| | | style="text-align:center;" | vv5 |
| | | style="text-align:center;" | double-down 5th |
| | | style="text-align:center;" | Avv |
| | |- |
| | | | 41 |
| | | | 683.333 |
| | | | 40/27 |
| | | style="text-align:center;" | v5 |
| | | style="text-align:center;" | down 5th |
| | | style="text-align:center;" | Av |
| | |- |
| | | | 42 |
| | | | 700 |
| | | | 3/2 |
| | | style="text-align:center;" | P5 |
| | | style="text-align:center;" | perfect 5th |
| | | style="text-align:center;" | A |
| | |- |
| | | | 43 |
| | | | 716.667 |
| | | | 50/33 |
| | | style="text-align:center;" | ^5 |
| | | style="text-align:center;" | up 5th |
| | | style="text-align:center;" | A^ |
| | |- |
| | | | 44 |
| | | | 733.333 |
| | | | 32/21 |
| | | style="text-align:center;" | ^^5 |
| | | style="text-align:center;" | double-up 5th |
| | | style="text-align:center;" | A^^ |
| | |- |
| | | | 45 |
| | | | 750 |
| | | | 54/35 |
| | | style="text-align:center;" | ^<span style="font-size: 90%; vertical-align: super;">3</span>5, v<span style="font-size: 90%; vertical-align: super;">3</span>m6 |
| | | style="text-align:center;" | triple-up 5th, |
|
| |
|
| =Music= | | triple-down minor 6th |
| [[http://www.archive.org/details/Kotekant|Kotekant]] //[[http://www.archive.org/download/Kotekant/kotekant.mp3|play]]// by [[xenharmonic/Gene Ward Smith|Gene Ward Smith]]
| | | style="text-align:center;" | A^<span style="font-size: 90%; vertical-align: super;">3</span>, Bbv<span style="font-size: 90%; vertical-align: super;">3</span> |
| //[[http://micro.soonlabel.com/gene_ward_smith/Others/Meneghin/Claudi-Meneghin-Twinkle-canon-72-edo.mp3|Twinkle canon – 72 edo]]// by [[http://soonlabel.com/xenharmonic/archives/573|Claudi Meneghin]]
| | |- |
| //[[http://micro.soonlabel.com/gene_ward_smith/Others/Freivald/Lazy%20Sunday.mp3|Lazy Sunday]]// by [[Jake Freivald]] in the [[lazysunday]] scale.
| | | | 46 |
| //[[http://micro.soonlabel.com/gene_ward_smith/Others/Rodgers/drum12a-c-t9.mp3|June Gloom #9]]// by Prent Rodgers | | | | 766.667 |
| | | | 14/9 |
| | | style="text-align:center;" | vvm6 |
| | | style="text-align:center;" | double-downminor 6th |
| | | style="text-align:center;" | Bbvv |
| | |- |
| | | | 47 |
| | | | 783.333 |
| | | | 11/7 |
| | | style="text-align:center;" | vm6 |
| | | style="text-align:center;" | downminor 6th |
| | | style="text-align:center;" | Bbv |
| | |- |
| | | | 48 |
| | | | 800 |
| | | | 35/22 |
| | | style="text-align:center;" | m6 |
| | | style="text-align:center;" | minor 6th |
| | | style="text-align:center;" | Bb |
| | |- |
| | | | 49 |
| | | | 816.667 |
| | | | 8/5 |
| | | style="text-align:center;" | ^m6 |
| | | style="text-align:center;" | upminor 6th |
| | | style="text-align:center;" | Bb^ |
| | |- |
| | | | 50 |
| | | | 833.333 |
| | | | 81/50 |
| | | style="text-align:center;" | v~6 |
| | | style="text-align:center;" | downmid 6th |
| | | style="text-align:center;" | Bb^^ |
| | |- |
| | | | 51 |
| | | | 850 |
| | | | 18/11 |
| | | style="text-align:center;" | ~6 |
| | | style="text-align:center;" | mid 6th |
| | | style="text-align:center;" | Bv<span style="font-size: 90%; vertical-align: super;">3</span> |
| | |- |
| | | | 52 |
| | | | 866.667 |
| | | | 33/20 |
| | | style="text-align:center;" | ^~6 |
| | | style="text-align:center;" | upmid 6th |
| | | style="text-align:center;" | Bvv |
| | |- |
| | | | 53 |
| | | | 883.333 |
| | | | 5/3 |
| | | style="text-align:center;" | vM6 |
| | | style="text-align:center;" | downmajor 6th |
| | | style="text-align:center;" | Bv |
| | |- |
| | | | 54 |
| | | | 900 |
| | | | 27/16 |
| | | style="text-align:center;" | M6 |
| | | style="text-align:center;" | major 6th |
| | | style="text-align:center;" | B |
| | |- |
| | | | 55 |
| | | | 916.667 |
| | | | 56/33 |
| | | style="text-align:center;" | ^M6 |
| | | style="text-align:center;" | upmajor 6th |
| | | style="text-align:center;" | B^ |
| | |- |
| | | | 56 |
| | | | 933.333 |
| | | | 12/7 |
| | | style="text-align:center;" | ^^M6 |
| | | style="text-align:center;" | double-upmajor 6th |
| | | style="text-align:center;" | B^^ |
| | |- |
| | | | 57 |
| | | | 950 |
| | | | 121/70 |
| | | style="text-align:center;" | ^<span style="font-size: 90%; vertical-align: super;">3</span>M6, v<span style="font-size: 90%; vertical-align: super;">3</span>m7 |
| | | style="text-align:center;" | triple-up major 6th, |
|
| |
|
| =Scales= | | triple-down minor 7th |
| [[xenharmonic/smithgw72a|smithgw72a]], [[xenharmonic/smithgw72b|smithgw72b]], [[xenharmonic/smithgw72c|smithgw72c]], [[xenharmonic/smithgw72d|smithgw72d]], [[xenharmonic/smithgw72e|smithgw72e]], [[xenharmonic/smithgw72f|smithgw72f]], [[xenharmonic/smithgw72g|smithgw72g]], [[xenharmonic/smithgw72h|smithgw72h]], [[xenharmonic/smithgw72i|smithgw72i]], [[xenharmonic/smithgw72j|smithgw72j]]
| | | style="text-align:center;" | B^<span style="font-size: 90%; vertical-align: super;">3</span>, Cv<span style="font-size: 90%; vertical-align: super;">3</span> |
| [[xenharmonic/blackjack|blackjack]], [[xenharmonic/miracle_8|miracle_8]], [[xenharmonic/miracle_10|miracle_10]], [[xenharmonic/miracle_12|miracle_12]], [[xenharmonic/miracle_12a|miracle_12a]], [[xenharmonic/miracle_24hi|miracle_24hi]], [[xenharmonic/miracle_24lo|miracle_24lo]]
| | |- |
| [[xenharmonic/keenanmarvel|keenanmarvel]], [[xenharmonic/xenakis_chrome|xenakis_chrome]], [[xenharmonic/xenakis_diat|xenakis_diat]], [[xenharmonic/xenakis_schrome|xenakis_schrome]]
| | | | 58 |
| [[xenharmonic/genus24255et72|Euler(24255) genus in 72 equal]]
| | | | 966.667 |
| [[JuneGloom]]
| | | | 7/4 |
| | | style="text-align:center;" | vvm7 |
| | | style="text-align:center;" | double-downminor 7th |
| | | style="text-align:center;" | Cvv |
| | |- |
| | | | 59 |
| | | | 983.333 |
| | | | 44/25 |
| | | style="text-align:center;" | vm7 |
| | | style="text-align:center;" | downminor 7th |
| | | style="text-align:center;" | Cv |
| | |- |
| | | | 60 |
| | | | 1000 |
| | | | 16/9 |
| | | style="text-align:center;" | m7 |
| | | style="text-align:center;" | minor 7th |
| | | style="text-align:center;" | C |
| | |- |
| | | | 61 |
| | | | 1016.667 |
| | | | 9/5 |
| | | style="text-align:center;" | ^m7 |
| | | style="text-align:center;" | upminor 7th |
| | | style="text-align:center;" | C^ |
| | |- |
| | | | 62 |
| | | | 1033.333 |
| | | | 20/11 |
| | | style="text-align:center;" | v~7 |
| | | style="text-align:center;" | downmid 7th |
| | | style="text-align:center;" | C^^ |
| | |- |
| | | | 63 |
| | | | 1050 |
| | | | 11/6 |
| | | style="text-align:center;" | ~7 |
| | | style="text-align:center;" | mid 7th |
| | | style="text-align:center;" | C^<span style="font-size: 90%; vertical-align: super;">3</span> |
| | |- |
| | | | 64 |
| | | | 1066.667 |
| | | | 50/27 |
| | | style="text-align:center;" | ^~7 |
| | | style="text-align:center;" | upmin 7th |
| | | style="text-align:center;" | C#vv |
| | |- |
| | | | 65 |
| | | | 1083.333 |
| | | | 15/8 |
| | | style="text-align:center;" | vM7 |
| | | style="text-align:center;" | downmajor 7th |
| | | style="text-align:center;" | C#v |
| | |- |
| | | | 66 |
| | | | 1100 |
| | | | 66/35 |
| | | style="text-align:center;" | M7 |
| | | style="text-align:center;" | major 7th |
| | | style="text-align:center;" | C# |
| | |- |
| | | | 67 |
| | | | 1116.667 |
| | | | 21/11 |
| | | style="text-align:center;" | ^M7 |
| | | style="text-align:center;" | upmajor 7th |
| | | style="text-align:center;" | C#^ |
| | |- |
| | | | 68 |
| | | | 1133.333 |
| | | | 27/14 |
| | | style="text-align:center;" | ^^M7 |
| | | style="text-align:center;" | double-upmajor 7th |
| | | style="text-align:center;" | C#^^ |
| | |- |
| | | | 69 |
| | | | 1150 |
| | | | 35/18 |
| | | style="text-align:center;" | ^<span style="font-size: 90%; vertical-align: super;">3</span>M7, v<span style="font-size: 90%; vertical-align: super;">3</span>8 |
| | | style="text-align:center;" | triple-up major 7th, |
|
| |
|
| =External links=
| | triple-down octave |
| * [[http://en.wikipedia.org/wiki/72_tone_equal_temperament|Wikipedia article on 72edo]]
| | | style="text-align:center;" | C#^<span style="font-size: 90%; vertical-align: super;">3</span>, Dv<span style="font-size: 90%; vertical-align: super;">3</span> |
| * [[http://orthodoxwiki.org/Byzantine_Chant|OrthodoxWiki Article on Byzantine chant, which uses 72edo]]
| | |- |
| * [[http://en.wikipedia.org/wiki/Joe_Maneri|Wikipedia article on Joe Maneri (1927-2009)]]
| | | | 70 |
| * [[http://www.ekmelic-music.org/en/|Ekmelic Music Society/Gesellschaft für Ekmelische Musik]], a group of composers and researchers dedicated to 72edo music
| | | | 1166.667 |
| * [[http://72note.com/site/original.html|Rick Tagawa's 72edo site]], including theory and composers' list
| | | | 49/25 |
| * [[@http://www.myspace.com/dawier|Danny Wier, composer and musician who specializes in 72-edo]]</pre></div>
| | | style="text-align:center;" | vv8 |
| <h4>Original HTML content:</h4>
| | | style="text-align:center;" | double-down octave |
| <div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html"><html><head><title>72edo</title></head><body><!-- ws:start:WikiTextTocRule:18:&lt;img id=&quot;wikitext@@toc@@flat&quot; class=&quot;WikiMedia WikiMediaTocFlat&quot; title=&quot;Table of Contents&quot; src=&quot;/site/embedthumbnail/toc/flat?w=100&amp;h=16&quot;/&gt; --><!-- ws:end:WikiTextTocRule:18 --><!-- ws:start:WikiTextTocRule:19: --><a href="#Commas">Commas</a><!-- ws:end:WikiTextTocRule:19 --><!-- ws:start:WikiTextTocRule:20: --> | <a href="#Temperaments">Temperaments</a><!-- ws:end:WikiTextTocRule:20 --><!-- ws:start:WikiTextTocRule:21: --> | <a href="#Harmonic Scale">Harmonic Scale</a><!-- ws:end:WikiTextTocRule:21 --><!-- ws:start:WikiTextTocRule:22: --> | <a href="#Intervals">Intervals</a><!-- ws:end:WikiTextTocRule:22 --><!-- ws:start:WikiTextTocRule:23: --> | <a href="#Linear temperaments">Linear temperaments</a><!-- ws:end:WikiTextTocRule:23 --><!-- ws:start:WikiTextTocRule:24: --> | <a href="#Z function">Z function</a><!-- ws:end:WikiTextTocRule:24 --><!-- ws:start:WikiTextTocRule:25: --> | <a href="#Music">Music</a><!-- ws:end:WikiTextTocRule:25 --><!-- ws:start:WikiTextTocRule:26: --> | <a href="#Scales">Scales</a><!-- ws:end:WikiTextTocRule:26 --><!-- ws:start:WikiTextTocRule:27: --> | <a href="#External links">External links</a><!-- ws:end:WikiTextTocRule:27 --><!-- ws:start:WikiTextTocRule:28: -->
| | | style="text-align:center;" | Dvv |
| <!-- ws:end:WikiTextTocRule:28 --><hr />
| | |- |
| 72-tone equal temperament (or 72-edo) divides the octave into 72 steps or <em>moria</em>. This produces a twelfth-tone tuning, with the whole tone measuring 200 cents, the same as in 12-tone equal temperament. 72-tone is also a superset of <a class="wiki_link" href="https://xenharmonic.wikispaces.com/24edo">24-tone equal temperament</a>, a common and standard tuning of <a class="wiki_link" href="https://xenharmonic.wikispaces.com/Arabic%2C%20Turkish%2C%20Persian">Arabic</a> music, and has itself been used to tune Turkish music.<br />
| | | | 71 |
| <br />
| | | | 1183.333 |
| Composers that used 72-tone include Alois Hába, Ivan Wyschnegradsky, Julián Carillo (who is better associated with <a class="wiki_link" href="https://xenharmonic.wikispaces.com/96edo">96-edo</a>), Iannis Xenakis, Ezra Sims, James Tenney and the jazz musician Joe Maneri.<br />
| | | | 99/50 |
| <br />
| | | style="text-align:center;" | v8 |
| 72-tone equal temperament approximates <a class="wiki_link" href="https://xenharmonic.wikispaces.com/11-limit">11-limit just intonation</a> exceptionally well, is consistent in the <a class="wiki_link" href="https://xenharmonic.wikispaces.com/17-limit">17-limit</a>, and is the ninth <a class="wiki_link" href="https://xenharmonic.wikispaces.com/The%20Riemann%20Zeta%20Function%20and%20Tuning#Zeta%20EDO%20lists">Zeta integral tuning</a>. The octave, fifth and fourth are the same size as they would be in 12-tone, 72, 42 and 30 steps respectively, but the major third (5/4) measures 23 steps, not 24, and other major intervals are one step flat of 12-et while minor ones are one step sharp. The septimal minor seventh (7/4) is 58 steps, while the undecimal semiaugmented fourth (11/8) is 33.<br />
| | | style="text-align:center;" | down octave |
| <br />
| | | style="text-align:center;" | Dv |
| 72 is an excellent tuning for <a class="wiki_link" href="https://xenharmonic.wikispaces.com/Gamelismic%20clan">miracle temperament</a>, especially the 11-limit version, and the related rank three temperament <a class="wiki_link" href="https://xenharmonic.wikispaces.com/Marvel%20family#Prodigy">prodigy</a>, and is a good tuning for other temperaments and scales, including wizard, harry, catakleismic, compton, unidec and tritikleismic.<br />
| | |- |
| <br />
| | | | 72 |
| <!-- ws:start:WikiTextHeadingRule:0:&lt;h1&gt; --><h1 id="toc0"><a name="Commas"></a><!-- ws:end:WikiTextHeadingRule:0 -->Commas</h1>
| | | | 1200 |
| <br />
| | | | 2/1 |
| Commas tempered out by 72edo include...<br />
| | | style="text-align:center;" | P8 |
| <br />
| | | style="text-align:center;" | perfect octave |
| | | | style="text-align:center;" | D |
| | | |} |
| <table class="wiki_table">
| | Combining ups and downs notation with [[Kite's_color_notation|color notation]], qualities can be loosely associated with colors: |
| <tr>
| |
| <th>3-limit<br />
| |
| </th>
| |
| </tr>
| |
| <tr>
| |
| <td>Pythagorean comma = 531441/524288 = |-19 12&gt;<br />
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| | |
| <br />
| |
| | |
| | |
| <table class="wiki_table">
| |
| <tr>
| |
| <th>5-limit<br />
| |
| </th>
| |
| </tr>
| |
| <tr>
| |
| <td>kleisma = 15625/15552 = |-6 -5 6&gt;<br />
| |
| ampersand = 34171875/33554432 = |-25 7 6&gt;<br />
| |
| graviton = 129140163/128000000 = |-13 17 -6&gt;<br />
| |
| ennealimma = 7629394531250/7625597484987 = |1 -27 18&gt;<br />
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| | |
| <br />
| |
|
| |
|
| | {| class="wikitable" |
| | |- |
| | ! | quality |
| | ! | color |
| | ! | monzo format |
| | ! | examples |
| | |- |
| | | style="text-align:center;" | double-down minor |
| | | style="text-align:center;" | blue |
| | | style="text-align:center;" | {a, b, 0, 1} |
| | | style="text-align:center;" | 7/6, 7/4 |
| | |- |
| | | style="text-align:center;" | minor |
| | | style="text-align:center;" | fourthward white |
| | | style="text-align:center;" | {a, b}, b < -1 |
| | | style="text-align:center;" | 32/27, 16/9 |
| | |- |
| | | style="text-align:center;" | upminor |
| | | style="text-align:center;" | green |
| | | style="text-align:center;" | {a, b, -1} |
| | | style="text-align:center;" | 6/5, 9/5 |
| | |- |
| | | style="text-align:center;" | mid |
| | | style="text-align:center;" | jade |
| | | style="text-align:center;" | {a, b, 0, 0, 1} |
| | | style="text-align:center;" | 11/9, 11/6 |
| | |- |
| | | style="text-align:center;" | " |
| | | style="text-align:center;" | amber |
| | | style="text-align:center;" | {a, b, 0, 0, -1} |
| | | style="text-align:center;" | 12/11, 18/11 |
| | |- |
| | | style="text-align:center;" | downmajor |
| | | style="text-align:center;" | yellow |
| | | style="text-align:center;" | {a, b, 1} |
| | | style="text-align:center;" | 5/4, 5/3 |
| | |- |
| | | style="text-align:center;" | major |
| | | style="text-align:center;" | fifthward white |
| | | style="text-align:center;" | {a, b}, b > 1 |
| | | style="text-align:center;" | 9/8, 27/16 |
| | |- |
| | | style="text-align:center;" | double-up major |
| | | style="text-align:center;" | red |
| | | style="text-align:center;" | {a, b, 0, -1} |
| | | style="text-align:center;" | 9/7, 12/7 |
| | |} |
| | All 72edo chords can be named using ups and downs. Here are the blue, green, jade, yellow and red triads: |
|
| |
|
| <table class="wiki_table">
| | {| class="wikitable" |
| <tr>
| | |- |
| <th>7-limit<br />
| | ! | color of the 3rd |
| </th>
| | ! | JI chord |
| <th>11-limit<br />
| | ! | notes as edosteps |
| </th>
| | ! | notes of C chord |
| <th>13-limit<br />
| | ! | written name |
| </th>
| | ! | spoken name |
| </tr>
| | |- |
| <tr>
| | | style="text-align:center;" | blue |
| <td>...............................<br />
| | | style="text-align:center;" | 6:7:9 |
| 225/224<br />
| | | style="text-align:center;" | 0-16-42 |
| 1029/1024<br />
| | | style="text-align:center;" | C Ebvv G |
| 2401/2400<br />
| | | style="text-align:center;" | C.vvm |
| 4375/4374<br />
| | | style="text-align:center;" | C double-down minor |
| 16875/16807<br />
| | |- |
| 19683/19600<br />
| | | style="text-align:center;" | green |
| 420175/419904<br />
| | | style="text-align:center;" | 10:12:15 |
| 250047/250000<br />
| | | style="text-align:center;" | 0-19-42 |
| </td>
| | | style="text-align:center;" | C Eb^ G |
| <td>.......................<br />
| | | style="text-align:center;" | C.^m |
| 243/242<br />
| | | style="text-align:center;" | C upminor |
| 385/384<br />
| | |- |
| 441/440<br />
| | | style="text-align:center;" | jade |
| 540/539<br />
| | | style="text-align:center;" | 18:22:27 |
| 1375/1372<br />
| | | style="text-align:center;" | 0-21-42 |
| 3025/3024<br />
| | | style="text-align:center;" | C Ev<span style="font-size: 90%; vertical-align: super;">3</span> G |
| 4000/3993<br />
| | | style="text-align:center;" | C~ |
| 6250/6237<br />
| | | style="text-align:center;" | C mid |
| 9801/9800<br />
| | |- |
| </td>
| | | style="text-align:center;" | yellow |
| <td>.......................<br />
| | | style="text-align:center;" | 4:5:6 |
| 169/168<br />
| | | style="text-align:center;" | 0-23-42 |
| 325/324<br />
| | | style="text-align:center;" | C Ev G |
| 351/350<br />
| | | style="text-align:center;" | C.v |
| 364/363<br />
| | | style="text-align:center;" | C downmajor or C dot down |
| 625/624<br />
| | |- |
| 676/675<br />
| | | style="text-align:center;" | red |
| 729/728<br />
| | | style="text-align:center;" | 14:18:27 |
| 1001/1000<br />
| | | style="text-align:center;" | 0-26-42 |
| 1575/1573<br />
| | | style="text-align:center;" | C E^^ G |
| 1716/1715<br />
| | | style="text-align:center;" | C.^^ |
| 2080/2079<br />
| | | style="text-align:center;" | C double-upmajor or C dot double-up |
| 6656/6655<br />
| | |} |
| </td>
| | For a more complete list, see [[Ups_and_Downs_Notation#Chord names in other EDOs|Ups and Downs Notation - Chord names in other EDOs]]. |
| </tr>
| |
| </table>
| |
|
| |
|
| <br />
| | =Linear temperaments= |
| <!-- ws:start:WikiTextHeadingRule:2:&lt;h1&gt; --><h1 id="toc1"><a name="Temperaments"></a><!-- ws:end:WikiTextHeadingRule:2 -->Temperaments</h1>
| |
| <br />
| |
| It provides the optimal patent val for miracle and wizard in the 7-limit, miracle, catakleismic, bikleismic, compton, ennealimnic, ennealiminal, enneaportent, marvolo and catalytic in the 11-limit, and catakleismic, bikleismic, compton, comptone, enneaportent, ennealim, catalytic, marvolo, manna, hendec, lizard, neominor, hours, and semimiracle in the 13-limit.<br />
| |
| <br />
| |
| See also <a class="wiki_link" href="/List%20of%20edo-distinct%2072et%20rank%20two%20temperaments">List of edo-distinct 72et rank two temperaments</a>.<br />
| |
| <br />
| |
| <br />
| |
| <!-- ws:start:WikiTextHeadingRule:4:&lt;h1&gt; --><h1 id="toc2"><a name="Harmonic Scale"></a><!-- ws:end:WikiTextHeadingRule:4 -->Harmonic Scale</h1>
| |
| Mode 8 of the harmonic series -- <a class="wiki_link" href="https://xenharmonic.wikispaces.com/overtone%20scales">overtones 8 through 16</a>, octave repeating -- is well-represented in 72edo. Note that all the different step sizes are distinguished, except for 13:12 and 14:13 (conflated to 8\72edo, 133.3 cents) and 15:14 and 16:15 (conflated to 7\72edo, 116.7 cents, the generator for miracle temperament).<br />
| |
| <br />
| |
|
| |
|
| | {| class="wikitable" |
| | |- |
| | ! | Periods per octave |
| | ! | Generator |
| | ! | Names |
| | |- |
| | | | 1 |
| | | | 1\72 |
| | | | [[Quincy|quincy]] |
| | |- |
| | | | 1 |
| | | | 5\72 |
| | | | [[marvolo|marvolo]] |
| | |- |
| | | | 1 |
| | | | 7\72 |
| | | | [[Miracle|miracle]]/benediction/manna |
| | |- |
| | | | 1 |
| | | | 11\72 |
| | | | |
| | |- |
| | | | 1 |
| | | | 13\72 |
| | | | |
| | |- |
| | | | 1 |
| | | | 17\72 |
| | | | [[Neominor|neominor]] |
| | |- |
| | | | 1 |
| | | | 19\72 |
| | | | [[catakleismic|catakleismic]] |
| | |- |
| | | | 1 |
| | | | 23\72 |
| | | | |
| | |- |
| | | | 1 |
| | | | 25\72 |
| | | | [[Sqrtphi|sqrtphi]] |
| | |- |
| | | | 1 |
| | | | 29\72 |
| | | | |
| | |- |
| | | | 1 |
| | | | 31\72 |
| | | | [[Marvo|marvo]]/zarvo |
| | |- |
| | | | 1 |
| | | | 35\72 |
| | | | [[cotritone|cotritone]] |
| | |- |
| | | | 2 |
| | | | 1\72 |
| | | | |
| | |- |
| | | | 2 |
| | | | 5\72 |
| | | | [[Harry|harry]] |
| | |- |
| | | | 2 |
| | | | 7\72 |
| | | | |
| | |- |
| | | | 2 |
| | | | 11\72 |
| | | | [[Unidec|unidec]]/hendec |
| | |- |
| | | | 2 |
| | | | 13\72 |
| | | | [[wizard|wizard]]/lizard/gizzard |
| | |- |
| | | | 2 |
| | | | 17\72 |
| | | | |
| | |- |
| | | | 3 |
| | | | 1\72 |
| | | | |
| | |- |
| | | | 3 |
| | | | 5\72 |
| | | | [[Tritikleismic|tritikleismic]] |
| | |- |
| | | | 3 |
| | | | 7\72 |
| | | | |
| | |- |
| | | | 3 |
| | | | 11\72 |
| | | | [[Mirkat|mirkat]] |
| | |- |
| | | | 4 |
| | | | 1\72 |
| | | | [[Quadritikleismic|quadritikleismic]] |
| | |- |
| | | | 4 |
| | | | 5\72 |
| | | | |
| | |- |
| | | | 4 |
| | | | 7\72 |
| | | | |
| | |- |
| | | | 6 |
| | | | 1\72 |
| | | | |
| | |- |
| | | | 6 |
| | | | 5\72 |
| | | | |
| | |- |
| | | | 8 |
| | | | 1\72 |
| | | | [[Octoid|octoid]] |
| | |- |
| | | | 8 |
| | | | 2\72 |
| | | | [[Octowerck|octowerck]] |
| | |- |
| | | | 8 |
| | | | 4\72 |
| | | | |
| | |- |
| | | | 9 |
| | | | 1\72 |
| | | | |
| | |- |
| | | | 9 |
| | | | 3\72 |
| | | | [[Ennealimmal|ennealimmal]]/ennealimmic |
| | |- |
| | | | 12 |
| | | | 1\72 |
| | | | [[Compton|compton]] |
| | |- |
| | | | 18 |
| | | | 1\72 |
| | | | [[Hemiennealimmal|hemiennealimmal]] |
| | |- |
| | | | 24 |
| | | | 1\72 |
| | | | [[Hours|hours]] |
| | |- |
| | | | 36 |
| | | | 1\72 |
| | | | |
| | |} |
|
| |
|
| <table class="wiki_table">
| | =Z function= |
| <tr>
| | 72edo is the ninth [[The_Riemann_Zeta_Function_and_Tuning#Zeta EDO lists|zeta integral edo]], as well as being a peak and gap edo, and the maximum value of the [[The_Riemann_Zeta_Function_and_Tuning#The Z function|Z function]] in the region near 72 occurs at 71.9506, giving an octave of 1200.824 cents, the stretched octaves of the zeta tuning. Below is a plot of Z in the region around 72. |
| <td>Overtones in &quot;Mode 8&quot;:<br />
| |
| </td>
| |
| <td>8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>9<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>10<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>11<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>12<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>13<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>14<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>15<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>16<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>...as JI Ratio from 1/1:<br />
| |
| </td>
| |
| <td>1/1<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>9/8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>5/4<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>11/8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>3/2<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>13/8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>7/4<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>15/8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>2/1<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>...in cents:<br />
| |
| </td>
| |
| <td>0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>203.9<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>386.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>551.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>702.0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>840.5<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>968.8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>1088.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>1200.0<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>Nearest degree of 72edo:<br />
| |
| </td>
| |
| <td>0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>12<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>23<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>33<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>42<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>50<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>58<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>65<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>72<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>...in cents:<br />
| |
| </td>
| |
| <td>0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>200.0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>383.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>550.0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>700.0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>833.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>966.7<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>1083.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>1200.0<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>Steps as Freq. Ratio:<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>9:8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>10:9<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>11:10<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>12:11<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>13:12<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>14:13<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>15:14<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>16:15<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>...in cents:<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>203.9<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>182.4<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>165.0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>150.6<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>138.6<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>128.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>119.4<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>111.7<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>Nearest degree of 72edo:<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>12<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>11<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>10<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>9<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>8<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>7<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>7<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>...in cents:<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>200.0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>183.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>166.7<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>150.0<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>133.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>133.3<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>116.7<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| <td>116.7<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| </table>
| |
|
| |
|
| <br />
| | [[File:plot72.png|alt=plot72.png|plot72.png]] |
| <!-- ws:start:WikiTextHeadingRule:6:&lt;h1&gt; --><h1 id="toc3"><a name="Intervals"></a><!-- ws:end:WikiTextHeadingRule:6 -->Intervals</h1>
| |
|
| |
|
| |
|
| <table class="wiki_table">
| | =Music= |
| <tr>
| | [http://www.archive.org/details/Kotekant Kotekant] ''[http://www.archive.org/download/Kotekant/kotekant.mp3 play]'' by [[Gene_Ward_Smith|Gene Ward Smith]] |
| <td>degrees<br />
| |
| </td>
| |
| <td>cents value<br />
| |
| </td>
| |
| <td>approximate ratios (11-limit)<br />
| |
| </td>
| |
| <td colspan="3" style="text-align: center;"><a class="wiki_link" href="https://xenharmonic.wikispaces.com/Ups%20and%20Downs%20Notation">ups and downs </a><a class="wiki_link" href="https://xenharmonic.wikispaces.com/Ups%20and%20Downs%20Notation">notation</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>0<br />
| |
| </td>
| |
| <td>0<br />
| |
| </td>
| |
| <td>1/1<br />
| |
| </td>
| |
| <td style="text-align: center;">P1<br />
| |
| </td>
| |
| <td style="text-align: center;">perfect unison<br />
| |
| </td>
| |
| <td style="text-align: center;">D<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>16.667<br />
| |
| </td>
| |
| <td>81/80<br />
| |
| </td>
| |
| <td style="text-align: center;">^1<br />
| |
| </td>
| |
| <td style="text-align: center;">up unison<br />
| |
| </td>
| |
| <td style="text-align: center;">D^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>2<br />
| |
| </td>
| |
| <td>33.333<br />
| |
| </td>
| |
| <td>45/44<br />
| |
| </td>
| |
| <td style="text-align: center;">^^<br />
| |
| </td>
| |
| <td style="text-align: center;">double-up unison<br />
| |
| </td>
| |
| <td style="text-align: center;">D^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>3<br />
| |
| </td>
| |
| <td>50<br />
| |
| </td>
| |
| <td>33/32<br />
| |
| </td>
| |
| <td style="text-align: center;">^<span style="font-size: 90%; vertical-align: super;">3</span>1, v<span style="font-size: 90%; vertical-align: super;">3</span>m2<br />
| |
| </td>
| |
| <td style="text-align: center;">triple-up unison,<br />
| |
| triple-down minor 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">D^<span style="font-size: 90%; vertical-align: super;">3</span>, Ebv<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>4<br />
| |
| </td>
| |
| <td>66.667<br />
| |
| </td>
| |
| <td>25/24<br />
| |
| </td>
| |
| <td style="text-align: center;">vvm2<br />
| |
| </td>
| |
| <td style="text-align: center;">double-downminor 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">Ebvv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>5<br />
| |
| </td>
| |
| <td>83.333<br />
| |
| </td>
| |
| <td>21/20<br />
| |
| </td>
| |
| <td style="text-align: center;">vm2<br />
| |
| </td>
| |
| <td style="text-align: center;">downminor 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">Ebv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>6<br />
| |
| </td>
| |
| <td>100<br />
| |
| </td>
| |
| <td>35/33<br />
| |
| </td>
| |
| <td style="text-align: center;">m2<br />
| |
| </td>
| |
| <td style="text-align: center;">minor 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">Eb<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>7<br />
| |
| </td>
| |
| <td>116.667<br />
| |
| </td>
| |
| <td>15/14<br />
| |
| </td>
| |
| <td style="text-align: center;">^m2<br />
| |
| </td>
| |
| <td style="text-align: center;">upminor 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">Eb^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>8<br />
| |
| </td>
| |
| <td>133.333<br />
| |
| </td>
| |
| <td>27/25<br />
| |
| </td>
| |
| <td style="text-align: center;">v~2<br />
| |
| </td>
| |
| <td style="text-align: center;">downmid 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">Eb^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>9<br />
| |
| </td>
| |
| <td>150<br />
| |
| </td>
| |
| <td>12/11<br />
| |
| </td>
| |
| <td style="text-align: center;">~2<br />
| |
| </td>
| |
| <td style="text-align: center;">mid 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">Ev<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>10<br />
| |
| </td>
| |
| <td>166.667<br />
| |
| </td>
| |
| <td>11/10<br />
| |
| </td>
| |
| <td style="text-align: center;">^~2<br />
| |
| </td>
| |
| <td style="text-align: center;">upmid 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">Evv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>11<br />
| |
| </td>
| |
| <td>183.333<br />
| |
| </td>
| |
| <td>10/9<br />
| |
| </td>
| |
| <td style="text-align: center;">vM2<br />
| |
| </td>
| |
| <td style="text-align: center;">downmajor 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">Ev<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>12<br />
| |
| </td>
| |
| <td>200<br />
| |
| </td>
| |
| <td>9/8<br />
| |
| </td>
| |
| <td style="text-align: center;">M2<br />
| |
| </td>
| |
| <td style="text-align: center;">major 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">E<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>13<br />
| |
| </td>
| |
| <td>216.667<br />
| |
| </td>
| |
| <td>25/22<br />
| |
| </td>
| |
| <td style="text-align: center;">^M2<br />
| |
| </td>
| |
| <td style="text-align: center;">upmajor 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">E^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>14<br />
| |
| </td>
| |
| <td>233.333<br />
| |
| </td>
| |
| <td>8/7<br />
| |
| </td>
| |
| <td style="text-align: center;">^^M2<br />
| |
| </td>
| |
| <td style="text-align: center;">double-upmajor 2nd<br />
| |
| </td>
| |
| <td style="text-align: center;">E^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>15<br />
| |
| </td>
| |
| <td>250<br />
| |
| </td>
| |
| <td>81/70<br />
| |
| </td>
| |
| <td style="text-align: center;">^<span style="font-size: 90%; vertical-align: super;">3</span>M2, v<span style="font-size: 90%; vertical-align: super;">3</span>m3<br />
| |
| </td>
| |
| <td style="text-align: center;">triple-up major 2nd,<br />
| |
| triple-down minor 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">E^<span style="font-size: 90%; vertical-align: super;">3</span>, Fv<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>16<br />
| |
| </td>
| |
| <td>266.667<br />
| |
| </td>
| |
| <td>7/6<br />
| |
| </td>
| |
| <td style="text-align: center;">vvm3<br />
| |
| </td>
| |
| <td style="text-align: center;">double-downminor 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">Fvv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>17<br />
| |
| </td>
| |
| <td>283.333<br />
| |
| </td>
| |
| <td>33/28<br />
| |
| </td>
| |
| <td style="text-align: center;">vm3<br />
| |
| </td>
| |
| <td style="text-align: center;">downminor 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">Fv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>18<br />
| |
| </td>
| |
| <td>300<br />
| |
| </td>
| |
| <td>25/21<br />
| |
| </td>
| |
| <td style="text-align: center;">m3<br />
| |
| </td>
| |
| <td style="text-align: center;">minor 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>19<br />
| |
| </td>
| |
| <td>316.667<br />
| |
| </td>
| |
| <td>6/5<br />
| |
| </td>
| |
| <td style="text-align: center;">^m3<br />
| |
| </td>
| |
| <td style="text-align: center;">upminor 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>20<br />
| |
| </td>
| |
| <td>333.333<br />
| |
| </td>
| |
| <td>40/33<br />
| |
| </td>
| |
| <td style="text-align: center;">v~3<br />
| |
| </td>
| |
| <td style="text-align: center;">downmid 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>21<br />
| |
| </td>
| |
| <td>350<br />
| |
| </td>
| |
| <td>11/9<br />
| |
| </td>
| |
| <td style="text-align: center;">~3<br />
| |
| </td>
| |
| <td style="text-align: center;">mid 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F^<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>22<br />
| |
| </td>
| |
| <td>366.667<br />
| |
| </td>
| |
| <td>99/80<br />
| |
| </td>
| |
| <td style="text-align: center;">^~3<br />
| |
| </td>
| |
| <td style="text-align: center;">upmid 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F#vv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>23<br />
| |
| </td>
| |
| <td>383.333<br />
| |
| </td>
| |
| <td>5/4<br />
| |
| </td>
| |
| <td style="text-align: center;">vM3<br />
| |
| </td>
| |
| <td style="text-align: center;">downmajor 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F#v<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>24<br />
| |
| </td>
| |
| <td>400<br />
| |
| </td>
| |
| <td>44/35<br />
| |
| </td>
| |
| <td style="text-align: center;">M3<br />
| |
| </td>
| |
| <td style="text-align: center;">major 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F#<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>25<br />
| |
| </td>
| |
| <td>416.667<br />
| |
| </td>
| |
| <td>14/11<br />
| |
| </td>
| |
| <td style="text-align: center;">^M3<br />
| |
| </td>
| |
| <td style="text-align: center;">upmajor 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F#^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>26<br />
| |
| </td>
| |
| <td>433.333<br />
| |
| </td>
| |
| <td>9/7<br />
| |
| </td>
| |
| <td style="text-align: center;">^^M3<br />
| |
| </td>
| |
| <td style="text-align: center;">double-upmajor 3rd<br />
| |
| </td>
| |
| <td style="text-align: center;">F#^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>27<br />
| |
| </td>
| |
| <td>450<br />
| |
| </td>
| |
| <td>35/27<br />
| |
| </td>
| |
| <td style="text-align: center;">^<span style="font-size: 90%; vertical-align: super;">3</span>M3, v<span style="font-size: 90%; vertical-align: super;">3</span>4<br />
| |
| </td>
| |
| <td style="text-align: center;">triple-up major 3rd,<br />
| |
| triple-down 4th<br />
| |
| </td>
| |
| <td style="text-align: center;">F#^<span style="font-size: 90%; vertical-align: super;">3</span>, Gv<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>28<br />
| |
| </td>
| |
| <td>466.667<br />
| |
| </td>
| |
| <td>21/16<br />
| |
| </td>
| |
| <td style="text-align: center;">vv4<br />
| |
| </td>
| |
| <td style="text-align: center;">double-down 4th<br />
| |
| </td>
| |
| <td style="text-align: center;">Gvv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>29<br />
| |
| </td>
| |
| <td>483.333<br />
| |
| </td>
| |
| <td>33/25<br />
| |
| </td>
| |
| <td style="text-align: center;">v4<br />
| |
| </td>
| |
| <td style="text-align: center;">down 4th<br />
| |
| </td>
| |
| <td style="text-align: center;">Gv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>30<br />
| |
| </td>
| |
| <td>500<br />
| |
| </td>
| |
| <td>4/3<br />
| |
| </td>
| |
| <td style="text-align: center;">P4<br />
| |
| </td>
| |
| <td style="text-align: center;">perfect 4th<br />
| |
| </td>
| |
| <td style="text-align: center;">G<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>31<br />
| |
| </td>
| |
| <td>516.667<br />
| |
| </td>
| |
| <td>27/20<br />
| |
| </td>
| |
| <td style="text-align: center;">^4<br />
| |
| </td>
| |
| <td style="text-align: center;">up 4th<br />
| |
| </td>
| |
| <td style="text-align: center;">G^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>32<br />
| |
| </td>
| |
| <td>533.333<br />
| |
| </td>
| |
| <td>15/11<br />
| |
| </td>
| |
| <td style="text-align: center;">^^4<br />
| |
| </td>
| |
| <td style="text-align: center;">double-up 4th<br />
| |
| </td>
| |
| <td style="text-align: center;">G^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>33<br />
| |
| </td>
| |
| <td>550<br />
| |
| </td>
| |
| <td>11/8<br />
| |
| </td>
| |
| <td style="text-align: center;">^<span style="font-size: 90%; vertical-align: super;">3</span>4<br />
| |
| </td>
| |
| <td style="text-align: center;">triple-up 4th<br />
| |
| </td>
| |
| <td style="text-align: center;">G^<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>34<br />
| |
| </td>
| |
| <td>566.667<br />
| |
| </td>
| |
| <td>25/18<br />
| |
| </td>
| |
| <td style="text-align: center;">vvA4<br />
| |
| </td>
| |
| <td style="text-align: center;">double-down aug 4th<br />
| |
| </td>
| |
| <td style="text-align: center;">G#vv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>35<br />
| |
| </td>
| |
| <td>583.333<br />
| |
| </td>
| |
| <td>7/5<br />
| |
| </td>
| |
| <td style="text-align: center;">vA4, vd5<br />
| |
| </td>
| |
| <td style="text-align: center;">downaug 4th, updim 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">G#v, Abv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>36<br />
| |
| </td>
| |
| <td>600<br />
| |
| </td>
| |
| <td>99/70<br />
| |
| </td>
| |
| <td style="text-align: center;">A4, d5<br />
| |
| </td>
| |
| <td style="text-align: center;">aug 4th, dim 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">G#, Ab<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>37<br />
| |
| </td>
| |
| <td>616.667<br />
| |
| </td>
| |
| <td>10/7<br />
| |
| </td>
| |
| <td style="text-align: center;">^A4, ^d5<br />
| |
| </td>
| |
| <td style="text-align: center;">upaug 4th, downdim 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">G#^, Ab^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>38<br />
| |
| </td>
| |
| <td>633.333<br />
| |
| </td>
| |
| <td>36/25<br />
| |
| </td>
| |
| <td style="text-align: center;">^^d5<br />
| |
| </td>
| |
| <td style="text-align: center;">double-updim 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">Ab^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>39<br />
| |
| </td>
| |
| <td>650<br />
| |
| </td>
| |
| <td>16/11<br />
| |
| </td>
| |
| <td style="text-align: center;">v<span style="font-size: 90%; vertical-align: super;">3</span>5<br />
| |
| </td>
| |
| <td style="text-align: center;">triple-down 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">Av<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>40<br />
| |
| </td>
| |
| <td>666.667<br />
| |
| </td>
| |
| <td>22/15<br />
| |
| </td>
| |
| <td style="text-align: center;">vv5<br />
| |
| </td>
| |
| <td style="text-align: center;">double-down 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">Avv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>41<br />
| |
| </td>
| |
| <td>683.333<br />
| |
| </td>
| |
| <td>40/27<br />
| |
| </td>
| |
| <td style="text-align: center;">v5<br />
| |
| </td>
| |
| <td style="text-align: center;">down 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">Av<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>42<br />
| |
| </td>
| |
| <td>700<br />
| |
| </td>
| |
| <td>3/2<br />
| |
| </td>
| |
| <td style="text-align: center;">P5<br />
| |
| </td>
| |
| <td style="text-align: center;">perfect 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">A<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>43<br />
| |
| </td>
| |
| <td>716.667<br />
| |
| </td>
| |
| <td>50/33<br />
| |
| </td>
| |
| <td style="text-align: center;">^5<br />
| |
| </td>
| |
| <td style="text-align: center;">up 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">A^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>44<br />
| |
| </td>
| |
| <td>733.333<br />
| |
| </td>
| |
| <td>32/21<br />
| |
| </td>
| |
| <td style="text-align: center;">^^5<br />
| |
| </td>
| |
| <td style="text-align: center;">double-up 5th<br />
| |
| </td>
| |
| <td style="text-align: center;">A^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>45<br />
| |
| </td>
| |
| <td>750<br />
| |
| </td>
| |
| <td>54/35<br />
| |
| </td>
| |
| <td style="text-align: center;">^<span style="font-size: 90%; vertical-align: super;">3</span>5, v<span style="font-size: 90%; vertical-align: super;">3</span>m6<br />
| |
| </td>
| |
| <td style="text-align: center;">triple-up 5th,<br />
| |
| triple-down minor 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">A^<span style="font-size: 90%; vertical-align: super;">3</span>, Bbv<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>46<br />
| |
| </td>
| |
| <td>766.667<br />
| |
| </td>
| |
| <td>14/9<br />
| |
| </td>
| |
| <td style="text-align: center;">vvm6<br />
| |
| </td>
| |
| <td style="text-align: center;">double-downminor 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">Bbvv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>47<br />
| |
| </td>
| |
| <td>783.333<br />
| |
| </td>
| |
| <td>11/7<br />
| |
| </td>
| |
| <td style="text-align: center;">vm6<br />
| |
| </td>
| |
| <td style="text-align: center;">downminor 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">Bbv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>48<br />
| |
| </td>
| |
| <td>800<br />
| |
| </td>
| |
| <td>35/22<br />
| |
| </td>
| |
| <td style="text-align: center;">m6<br />
| |
| </td>
| |
| <td style="text-align: center;">minor 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">Bb<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>49<br />
| |
| </td>
| |
| <td>816.667<br />
| |
| </td>
| |
| <td>8/5<br />
| |
| </td>
| |
| <td style="text-align: center;">^m6<br />
| |
| </td>
| |
| <td style="text-align: center;">upminor 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">Bb^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>50<br />
| |
| </td>
| |
| <td>833.333<br />
| |
| </td>
| |
| <td>81/50<br />
| |
| </td>
| |
| <td style="text-align: center;">v~6<br />
| |
| </td>
| |
| <td style="text-align: center;">downmid 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">Bb^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>51<br />
| |
| </td>
| |
| <td>850<br />
| |
| </td>
| |
| <td>18/11<br />
| |
| </td>
| |
| <td style="text-align: center;">~6<br />
| |
| </td>
| |
| <td style="text-align: center;">mid 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">Bv<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>52<br />
| |
| </td>
| |
| <td>866.667<br />
| |
| </td>
| |
| <td>33/20<br />
| |
| </td>
| |
| <td style="text-align: center;">^~6<br />
| |
| </td>
| |
| <td style="text-align: center;">upmid 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">Bvv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>53<br />
| |
| </td>
| |
| <td>883.333<br />
| |
| </td>
| |
| <td>5/3<br />
| |
| </td>
| |
| <td style="text-align: center;">vM6<br />
| |
| </td>
| |
| <td style="text-align: center;">downmajor 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">Bv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>54<br />
| |
| </td>
| |
| <td>900<br />
| |
| </td>
| |
| <td>27/16<br />
| |
| </td>
| |
| <td style="text-align: center;">M6<br />
| |
| </td>
| |
| <td style="text-align: center;">major 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">B<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>55<br />
| |
| </td>
| |
| <td>916.667<br />
| |
| </td>
| |
| <td>56/33<br />
| |
| </td>
| |
| <td style="text-align: center;">^M6<br />
| |
| </td>
| |
| <td style="text-align: center;">upmajor 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">B^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>56<br />
| |
| </td>
| |
| <td>933.333<br />
| |
| </td>
| |
| <td>12/7<br />
| |
| </td>
| |
| <td style="text-align: center;">^^M6<br />
| |
| </td>
| |
| <td style="text-align: center;">double-upmajor 6th<br />
| |
| </td>
| |
| <td style="text-align: center;">B^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>57<br />
| |
| </td>
| |
| <td>950<br />
| |
| </td>
| |
| <td>121/70<br />
| |
| </td>
| |
| <td style="text-align: center;">^<span style="font-size: 90%; vertical-align: super;">3</span>M6, v<span style="font-size: 90%; vertical-align: super;">3</span>m7<br />
| |
| </td>
| |
| <td style="text-align: center;">triple-up major 6th,<br />
| |
| triple-down minor 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">B^<span style="font-size: 90%; vertical-align: super;">3</span>, Cv<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>58<br />
| |
| </td>
| |
| <td>966.667<br />
| |
| </td>
| |
| <td>7/4<br />
| |
| </td>
| |
| <td style="text-align: center;">vvm7<br />
| |
| </td>
| |
| <td style="text-align: center;">double-downminor 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">Cvv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>59<br />
| |
| </td>
| |
| <td>983.333<br />
| |
| </td>
| |
| <td>44/25<br />
| |
| </td>
| |
| <td style="text-align: center;">vm7<br />
| |
| </td>
| |
| <td style="text-align: center;">downminor 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">Cv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>60<br />
| |
| </td>
| |
| <td>1000<br />
| |
| </td>
| |
| <td>16/9<br />
| |
| </td>
| |
| <td style="text-align: center;">m7<br />
| |
| </td>
| |
| <td style="text-align: center;">minor 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>61<br />
| |
| </td>
| |
| <td>1016.667<br />
| |
| </td>
| |
| <td>9/5<br />
| |
| </td>
| |
| <td style="text-align: center;">^m7<br />
| |
| </td>
| |
| <td style="text-align: center;">upminor 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>62<br />
| |
| </td>
| |
| <td>1033.333<br />
| |
| </td>
| |
| <td>20/11<br />
| |
| </td>
| |
| <td style="text-align: center;">v~7<br />
| |
| </td>
| |
| <td style="text-align: center;">downmid 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>63<br />
| |
| </td>
| |
| <td>1050<br />
| |
| </td>
| |
| <td>11/6<br />
| |
| </td>
| |
| <td style="text-align: center;">~7<br />
| |
| </td>
| |
| <td style="text-align: center;">mid 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C^<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>64<br />
| |
| </td>
| |
| <td>1066.667<br />
| |
| </td>
| |
| <td>50/27<br />
| |
| </td>
| |
| <td style="text-align: center;">^~7<br />
| |
| </td>
| |
| <td style="text-align: center;">upmin 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C#vv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>65<br />
| |
| </td>
| |
| <td>1083.333<br />
| |
| </td>
| |
| <td>15/8<br />
| |
| </td>
| |
| <td style="text-align: center;">vM7<br />
| |
| </td>
| |
| <td style="text-align: center;">downmajor 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C#v<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>66<br />
| |
| </td>
| |
| <td>1100<br />
| |
| </td>
| |
| <td>66/35<br />
| |
| </td>
| |
| <td style="text-align: center;">M7<br />
| |
| </td>
| |
| <td style="text-align: center;">major 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C#<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>67<br />
| |
| </td>
| |
| <td>1116.667<br />
| |
| </td>
| |
| <td>21/11<br />
| |
| </td>
| |
| <td style="text-align: center;">^M7<br />
| |
| </td>
| |
| <td style="text-align: center;">upmajor 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C#^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>68<br />
| |
| </td>
| |
| <td>1133.333<br />
| |
| </td>
| |
| <td>27/14<br />
| |
| </td>
| |
| <td style="text-align: center;">^^M7<br />
| |
| </td>
| |
| <td style="text-align: center;">double-upmajor 7th<br />
| |
| </td>
| |
| <td style="text-align: center;">C#^^<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>69<br />
| |
| </td>
| |
| <td>1150<br />
| |
| </td>
| |
| <td>35/18<br />
| |
| </td>
| |
| <td style="text-align: center;">^<span style="font-size: 90%; vertical-align: super;">3</span>M7, v<span style="font-size: 90%; vertical-align: super;">3</span>8<br />
| |
| </td>
| |
| <td style="text-align: center;">triple-up major 7th,<br />
| |
| triple-down octave<br />
| |
| </td>
| |
| <td style="text-align: center;">C#^<span style="font-size: 90%; vertical-align: super;">3</span>, Dv<span style="font-size: 90%; vertical-align: super;">3</span><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>70<br />
| |
| </td>
| |
| <td>1166.667<br />
| |
| </td>
| |
| <td>49/25<br />
| |
| </td>
| |
| <td style="text-align: center;">vv8<br />
| |
| </td>
| |
| <td style="text-align: center;">double-down octave<br />
| |
| </td>
| |
| <td style="text-align: center;">Dvv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>71<br />
| |
| </td>
| |
| <td>1183.333<br />
| |
| </td>
| |
| <td>99/50<br />
| |
| </td>
| |
| <td style="text-align: center;">v8<br />
| |
| </td>
| |
| <td style="text-align: center;">down octave<br />
| |
| </td>
| |
| <td style="text-align: center;">Dv<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>72<br />
| |
| </td>
| |
| <td>1200<br />
| |
| </td>
| |
| <td>2/1<br />
| |
| </td>
| |
| <td style="text-align: center;">P8<br />
| |
| </td>
| |
| <td style="text-align: center;">perfect octave<br />
| |
| </td>
| |
| <td style="text-align: center;">D<br />
| |
| </td>
| |
| </tr>
| |
| </table>
| |
|
| |
|
| Combining ups and downs notation with <a class="wiki_link" href="/Kite%27s%20color%20notation">color notation</a>, qualities can be loosely associated with colors:<br />
| | ''[http://micro.soonlabel.com/gene_ward_smith/Others/Meneghin/Claudi-Meneghin-Twinkle-canon-72-edo.mp3 Twinkle canon – 72 edo]'' by [http://soonlabel.com/xenharmonic/archives/573 Claudi Meneghin] |
|
| |
|
| | ''[http://micro.soonlabel.com/gene_ward_smith/Others/Freivald/Lazy%20Sunday.mp3 Lazy Sunday]'' by [[Jake_Freivald|Jake Freivald]] in the [[lazysunday|lazysunday]] scale. |
|
| |
|
| <table class="wiki_table">
| | ''[http://micro.soonlabel.com/gene_ward_smith/Others/Rodgers/drum12a-c-t9.mp3 June Gloom #9]'' by Prent Rodgers |
| <tr>
| |
| <th>quality<br />
| |
| </th>
| |
| <th>color<br />
| |
| </th>
| |
| <th>monzo format<br />
| |
| </th>
| |
| <th>examples<br />
| |
| </th>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">double-down minor<br />
| |
| </td>
| |
| <td style="text-align: center;">blue<br />
| |
| </td>
| |
| <td style="text-align: center;">{a, b, 0, 1}<br />
| |
| </td>
| |
| <td style="text-align: center;">7/6, 7/4<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">minor<br />
| |
| </td>
| |
| <td style="text-align: center;">fourthward white<br />
| |
| </td>
| |
| <td style="text-align: center;">{a, b}, b &lt; -1<br />
| |
| </td>
| |
| <td style="text-align: center;">32/27, 16/9<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">upminor<br />
| |
| </td>
| |
| <td style="text-align: center;">green<br />
| |
| </td>
| |
| <td style="text-align: center;">{a, b, -1}<br />
| |
| </td>
| |
| <td style="text-align: center;">6/5, 9/5<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">mid<br />
| |
| </td>
| |
| <td style="text-align: center;">jade<br />
| |
| </td>
| |
| <td style="text-align: center;">{a, b, 0, 0, 1}<br />
| |
| </td>
| |
| <td style="text-align: center;">11/9, 11/6<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">&quot;<br />
| |
| </td>
| |
| <td style="text-align: center;">amber<br />
| |
| </td>
| |
| <td style="text-align: center;">{a, b, 0, 0, -1}<br />
| |
| </td>
| |
| <td style="text-align: center;">12/11, 18/11<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">downmajor<br />
| |
| </td>
| |
| <td style="text-align: center;">yellow<br />
| |
| </td>
| |
| <td style="text-align: center;">{a, b, 1}<br />
| |
| </td>
| |
| <td style="text-align: center;">5/4, 5/3<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">major<br />
| |
| </td>
| |
| <td style="text-align: center;">fifthward white<br />
| |
| </td>
| |
| <td style="text-align: center;">{a, b}, b &gt; 1<br />
| |
| </td>
| |
| <td style="text-align: center;">9/8, 27/16<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">double-up major<br />
| |
| </td>
| |
| <td style="text-align: center;">red<br />
| |
| </td>
| |
| <td style="text-align: center;">{a, b, 0, -1}<br />
| |
| </td>
| |
| <td style="text-align: center;">9/7, 12/7<br />
| |
| </td>
| |
| </tr>
| |
| </table>
| |
|
| |
|
| All 72edo chords can be named using ups and downs. Here are the blue, green, jade, yellow and red triads:<br />
| | =Scales= |
| | [[smithgw72a|smithgw72a]], [[smithgw72b|smithgw72b]], [[smithgw72c|smithgw72c]], [[smithgw72d|smithgw72d]], [[smithgw72e|smithgw72e]], [[smithgw72f|smithgw72f]], [[smithgw72g|smithgw72g]], [[smithgw72h|smithgw72h]], [[smithgw72i|smithgw72i]], [[smithgw72j|smithgw72j]] |
|
| |
|
| | [[blackjack|blackjack]], [[miracle_8|miracle_8]], [[miracle_10|miracle_10]], [[miracle_12|miracle_12]], [[miracle_12a|miracle_12a]], [[miracle_24hi|miracle_24hi]], [[miracle_24lo|miracle_24lo]] |
|
| |
|
| <table class="wiki_table">
| | [[keenanmarvel|keenanmarvel]], [[xenakis_chrome|xenakis_chrome]], [[xenakis_diat|xenakis_diat]], [[xenakis_schrome|xenakis_schrome]] |
| <tr>
| |
| <th>color of the 3rd<br />
| |
| </th>
| |
| <th>JI chord<br />
| |
| </th>
| |
| <th>notes as edosteps<br />
| |
| </th>
| |
| <th>notes of C chord<br />
| |
| </th>
| |
| <th>written name<br />
| |
| </th>
| |
| <th>spoken name<br />
| |
| </th>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">blue<br />
| |
| </td>
| |
| <td style="text-align: center;">6:7:9<br />
| |
| </td>
| |
| <td style="text-align: center;">0-16-42<br />
| |
| </td>
| |
| <td style="text-align: center;">C Ebvv G<br />
| |
| </td>
| |
| <td style="text-align: center;">C.vvm<br />
| |
| </td>
| |
| <td style="text-align: center;">C double-down minor<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">green<br />
| |
| </td>
| |
| <td style="text-align: center;">10:12:15<br />
| |
| </td>
| |
| <td style="text-align: center;">0-19-42<br />
| |
| </td>
| |
| <td style="text-align: center;">C Eb^ G<br />
| |
| </td>
| |
| <td style="text-align: center;">C.^m<br />
| |
| </td>
| |
| <td style="text-align: center;">C upminor<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">jade<br />
| |
| </td>
| |
| <td style="text-align: center;">18:22:27<br />
| |
| </td>
| |
| <td style="text-align: center;">0-21-42<br />
| |
| </td>
| |
| <td style="text-align: center;">C Ev<span style="font-size: 90%; vertical-align: super;">3</span> G<br />
| |
| </td>
| |
| <td style="text-align: center;">C~<br />
| |
| </td>
| |
| <td style="text-align: center;">C mid<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">yellow<br />
| |
| </td>
| |
| <td style="text-align: center;">4:5:6<br />
| |
| </td>
| |
| <td style="text-align: center;">0-23-42<br />
| |
| </td>
| |
| <td style="text-align: center;">C Ev G<br />
| |
| </td>
| |
| <td style="text-align: center;">C.v<br />
| |
| </td>
| |
| <td style="text-align: center;">C downmajor or C dot down<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td style="text-align: center;">red<br />
| |
| </td>
| |
| <td style="text-align: center;">14:18:27<br />
| |
| </td>
| |
| <td style="text-align: center;">0-26-42<br />
| |
| </td>
| |
| <td style="text-align: center;">C E^^ G<br />
| |
| </td>
| |
| <td style="text-align: center;">C.^^<br />
| |
| </td>
| |
| <td style="text-align: center;">C double-upmajor or C dot double-up<br />
| |
| </td>
| |
| </tr>
| |
| </table>
| |
|
| |
|
| For a more complete list, see <a class="wiki_link" href="https://xenharmonic.wikispaces.com/Ups%20and%20Downs%20Notation#Chord%20names%20in%20other%20EDOs">Ups and Downs Notation - Chord names in other EDOs</a>.<br />
| | [[genus24255et72|Euler(24255) genus in 72 equal]] |
| <br />
| |
| <!-- ws:start:WikiTextHeadingRule:8:&lt;h1&gt; --><h1 id="toc4"><a name="Linear temperaments"></a><!-- ws:end:WikiTextHeadingRule:8 -->Linear temperaments</h1>
| |
|
| |
|
| |
|
| <table class="wiki_table">
| | [[JuneGloom|JuneGloom]] |
| <tr>
| |
| <th>Periods per octave<br />
| |
| </th>
| |
| <th>Generator<br />
| |
| </th>
| |
| <th>Names<br />
| |
| </th>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/quincy">quincy</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>5\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="/marvolo">marvolo</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>7\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/miracle">miracle</a>/benediction/manna<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>11\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>13\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>17\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/neominor">neominor</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>19\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/catakleismic">catakleismic</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>23\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>25\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/sqrtphi">sqrtphi</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>29\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>31\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/marvo">marvo</a>/zarvo<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>1<br />
| |
| </td>
| |
| <td>35\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/cotritone">cotritone</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>2<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>2<br />
| |
| </td>
| |
| <td>5\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/harry">harry</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>2<br />
| |
| </td>
| |
| <td>7\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>2<br />
| |
| </td>
| |
| <td>11\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/unidec">unidec</a>/hendec<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>2<br />
| |
| </td>
| |
| <td>13\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/wizard">wizard</a>/lizard/gizzard<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>2<br />
| |
| </td>
| |
| <td>17\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>3<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>3<br />
| |
| </td>
| |
| <td>5\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/tritikleismic">tritikleismic</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>3<br />
| |
| </td>
| |
| <td>7\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>3<br />
| |
| </td>
| |
| <td>11\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/mirkat">mirkat</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>4<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/quadritikleismic">quadritikleismic</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>4<br />
| |
| </td>
| |
| <td>5\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>4<br />
| |
| </td>
| |
| <td>7\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>6<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>6<br />
| |
| </td>
| |
| <td>5\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>8<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/octoid">octoid</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>8<br />
| |
| </td>
| |
| <td>2\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/octowerck">octowerck</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>8<br />
| |
| </td>
| |
| <td>4\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>9<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>9<br />
| |
| </td>
| |
| <td>3\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/ennealimmal">ennealimmal</a>/ennealimmic<br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>12<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/compton">compton</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>18<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/hemiennealimmal">hemiennealimmal</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>24<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><a class="wiki_link" href="https://xenharmonic.wikispaces.com/hours">hours</a><br />
| |
| </td>
| |
| </tr>
| |
| <tr>
| |
| <td>36<br />
| |
| </td>
| |
| <td>1\72<br />
| |
| </td>
| |
| <td><br />
| |
| </td>
| |
| </tr>
| |
| </table>
| |
|
| |
|
| <br />
| | =External links= |
| <!-- ws:start:WikiTextHeadingRule:10:&lt;h1&gt; --><h1 id="toc5"><a name="Z function"></a><!-- ws:end:WikiTextHeadingRule:10 -->Z function</h1>
| | <ul><li>[http://en.wikipedia.org/wiki/72_tone_equal_temperament Wikipedia article on 72edo]</li><li>[http://orthodoxwiki.org/Byzantine_Chant OrthodoxWiki Article on Byzantine chant, which uses 72edo]</li><li>[http://en.wikipedia.org/wiki/Joe_Maneri Wikipedia article on Joe Maneri (1927-2009)]</li><li>[http://www.ekmelic-music.org/en/ Ekmelic Music Society/Gesellschaft für Ekmelische Musik], a group of composers and researchers dedicated to 72edo music</li><li>[http://72note.com/site/original.html Rick Tagawa's 72edo site], including theory and composers' list</li><li>[http://www.myspace.com/dawier Danny Wier, composer and musician who specializes in 72-edo]</li></ul> [[Category:edo]] |
| 72edo is the ninth <a class="wiki_link" href="https://xenharmonic.wikispaces.com/The%20Riemann%20Zeta%20Function%20and%20Tuning#Zeta%20EDO%20lists">zeta integral edo</a>, as well as being a peak and gap edo, and the maximum value of the <a class="wiki_link" href="https://xenharmonic.wikispaces.com/The%20Riemann%20Zeta%20Function%20and%20Tuning#The%20Z%20function">Z function</a> in the region near 72 occurs at 71.9506, giving an octave of 1200.824 cents, the stretched octaves of the zeta tuning. Below is a plot of Z in the region around 72.<br />
| | [[Category:listen]] |
| <br />
| | [[Category:marvel]] |
| <!-- ws:start:WikiTextLocalImageRule:1936:&lt;img src=&quot;https://xenharmonic.wikispaces.com/file/view/plot72.png/219772696/plot72.png&quot; alt=&quot;&quot; title=&quot;&quot; /&gt; --><img src="https://xenharmonic.wikispaces.com/file/view/plot72.png/219772696/plot72.png" alt="plot72.png" title="plot72.png" /><!-- ws:end:WikiTextLocalImageRule:1936 --><br />
| | [[Category:miracle]] |
| <br />
| | [[Category:moria]] |
| <!-- ws:start:WikiTextHeadingRule:12:&lt;h1&gt; --><h1 id="toc6"><a name="Music"></a><!-- ws:end:WikiTextHeadingRule:12 -->Music</h1>
| | [[Category:prodigy]] |
| <a class="wiki_link_ext" href="http://www.archive.org/details/Kotekant" rel="nofollow">Kotekant</a> <em><a class="wiki_link_ext" href="http://www.archive.org/download/Kotekant/kotekant.mp3" rel="nofollow">play</a></em> by <a class="wiki_link" href="https://xenharmonic.wikispaces.com/Gene%20Ward%20Smith">Gene Ward Smith</a><br />
| | [[Category:wizard]] |
| <em><a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Meneghin/Claudi-Meneghin-Twinkle-canon-72-edo.mp3" rel="nofollow">Twinkle canon – 72 edo</a></em> by <a class="wiki_link_ext" href="http://soonlabel.com/xenharmonic/archives/573" rel="nofollow">Claudi Meneghin</a><br />
| | [[Category:zeta]] |
| <em><a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Freivald/Lazy%20Sunday.mp3" rel="nofollow">Lazy Sunday</a></em> by <a class="wiki_link" href="/Jake%20Freivald">Jake Freivald</a> in the <a class="wiki_link" href="/lazysunday">lazysunday</a> scale.<br />
| |
| <em><a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Rodgers/drum12a-c-t9.mp3" rel="nofollow">June Gloom #9</a></em> by Prent Rodgers<br />
| |
| <br />
| |
| <!-- ws:start:WikiTextHeadingRule:14:&lt;h1&gt; --><h1 id="toc7"><a name="Scales"></a><!-- ws:end:WikiTextHeadingRule:14 -->Scales</h1>
| |
| <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72a">smithgw72a</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72b">smithgw72b</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72c">smithgw72c</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72d">smithgw72d</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72e">smithgw72e</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72f">smithgw72f</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72g">smithgw72g</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72h">smithgw72h</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72i">smithgw72i</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/smithgw72j">smithgw72j</a><br />
| |
| <a class="wiki_link" href="https://xenharmonic.wikispaces.com/blackjack">blackjack</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/miracle_8">miracle_8</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/miracle_10">miracle_10</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/miracle_12">miracle_12</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/miracle_12a">miracle_12a</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/miracle_24hi">miracle_24hi</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/miracle_24lo">miracle_24lo</a><br />
| |
| <a class="wiki_link" href="https://xenharmonic.wikispaces.com/keenanmarvel">keenanmarvel</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/xenakis_chrome">xenakis_chrome</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/xenakis_diat">xenakis_diat</a>, <a class="wiki_link" href="https://xenharmonic.wikispaces.com/xenakis_schrome">xenakis_schrome</a><br />
| |
| <a class="wiki_link" href="https://xenharmonic.wikispaces.com/genus24255et72">Euler(24255) genus in 72 equal</a><br />
| |
| <a class="wiki_link" href="/JuneGloom">JuneGloom</a><br />
| |
| <br />
| |
| <!-- ws:start:WikiTextHeadingRule:16:&lt;h1&gt; --><h1 id="toc8"><a name="External links"></a><!-- ws:end:WikiTextHeadingRule:16 -->External links</h1>
| |
| <ul><li><a class="wiki_link_ext" href="http://en.wikipedia.org/wiki/72_tone_equal_temperament" rel="nofollow">Wikipedia article on 72edo</a></li><li><a class="wiki_link_ext" href="http://orthodoxwiki.org/Byzantine_Chant" rel="nofollow">OrthodoxWiki Article on Byzantine chant, which uses 72edo</a></li><li><a class="wiki_link_ext" href="http://en.wikipedia.org/wiki/Joe_Maneri" rel="nofollow">Wikipedia article on Joe Maneri (1927-2009)</a></li><li><a class="wiki_link_ext" href="http://www.ekmelic-music.org/en/" rel="nofollow">Ekmelic Music Society/Gesellschaft für Ekmelische Musik</a>, a group of composers and researchers dedicated to 72edo music</li><li><a class="wiki_link_ext" href="http://72note.com/site/original.html" rel="nofollow">Rick Tagawa's 72edo site</a>, including theory and composers' list</li><li><a class="wiki_link_ext" href="http://www.myspace.com/dawier" rel="nofollow" target="_blank">Danny Wier, composer and musician who specializes in 72-edo</a></li></ul></body></html></pre></div>
| |