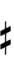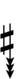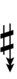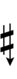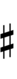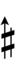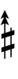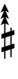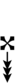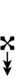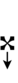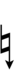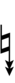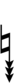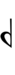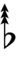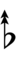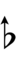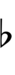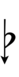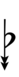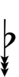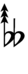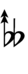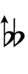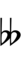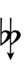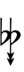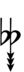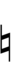47edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
BudjarnLambeth (talk | contribs)
autopatrolled, emailconfirmed
18,215 edits
BudjarnLambeth (talk | contribs)
autopatrolled, emailconfirmed
18,215 edits
 
(28 intermediate revisions by 7 users not shown)
Line 1: Line 1:
{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|47}}
{{ED intro}}
 
== Theory ==
== Theory ==
47edo has a fifth which is 12.593{{cent}} flat, unless you use the alternative fifth which is 12.939{{cent}} sharp, similar to 35edo. The soft diatonic scale generated from its flat fifth is so soft, with L/s = 7/6, that it stops sounding like [[meantone]] or even a [[flattone]] system like [[26edo]] or [[40edo]], but just sounds like a [[circulating temperament]] of [[7edo]]. It has therefore not aroused much interest, but its best approximation to 9/8 is actually quite good, one-third of a cent sharp. It does a good job of approximating the 2.9.5.7.33.13.17.57.69 23-limit [[k*N_subgroups|2*47 subgroup]] of the [[23-limit]], on which it tempers out the same commas as [[94edo]]. It provides a good tuning for [[Chromatic_pairs#Baldy|baldy]] and [[Chromatic_pairs#Silver|silver]] temperaments and relatives. It also provides a good tuning for [[baseball]] temperament.
47edo is the first edo that has two [[5L 2s|diatonic]] perfect fifths, as both fall between {{nowrap|4\7 {{=}} 686{{c}}}} and {{nowrap|3\5 {{=}} 720{{c}}}}. The fifth closest to [[3/2]] is 12.593-cent flat, unless you use the alternative fifth which is 12.939-cent sharp, similar to [[35edo]]. The soft diatonic scale generated from its flat fifth is so soft, with {{nowrap|L:s {{=}} 7:6}}, that it stops sounding like [[meantone]] or even a [[flattone]] system like [[26edo]] or [[40edo]], but just sounds like a [[circulating temperament]] of [[7edo]]. The hard diatonic scale generated from its sharp fifth is extremely hard, with {{nowrap|L:s {{=}} 9:1}}. It has therefore not aroused much interest, but its best approximation to [[9/8]] is actually quite good, one-third-of-a-cent sharp.


47edo is a diatonic edo because its 5th falls between 4\7 = 686{{cent}} and 3\5 = 720{{cent}}, as does its alternate 5th as well. 47edo is one of the most difficult diatonic edos to notate, because no other diatonic edos 5th is as flat (see [[42edo]] for the opposite extreme).
47edo is one of the most difficult diatonic edos to notate in [[native fifth notation|native fifths]], because no other diatonic edo's fifth is as extreme.  


A notation using the best 5th has major and minor 2nds of 7 and 6 edosteps respectively, with the naturals creating a 7edo-like scale:
=== Odd harmonics ===
{{Harmonics in equal|47}}


D * * * * * * E * * * * * F * * * * * * G * * * * * * A * * * * * * B * * * * * C * * * * * * D
47edo does a good job of approximating the 2.9.5.7.33.13.17.57.69 23-limit [[k*N subgroups|2*47 subgroup]] of the [[23-limit]], on which it tempers out the same commas as [[94edo]]. It provides a good tuning for [[baldy]] and [[silver]] and their relatives. It also provides a good tuning for the [[baseball]] temperament.


D# is next to D. This notation requires triple, quadruple and in some keys, quintuple or more sharps and flats. For example, a 0-15-27-38 chord (an approximate 4:5:6:7) on the note three edosteps above D would be spelled either as D#<sup>3</sup> - F#<sup>5</sup> - A#<sup>3</sup> - C# or as Eb<sup>4</sup> - Gbb - Ab<sup>4</sup> - Db<sup>6</sup>. This is an aug-three double-dim-seven chord, written D#<sup>3</sup>(A3)dd7 or Eb<sup>4</sup>(A3)dd7. It could also be called a sharp-three triple-flat-seven chord, written D#<sup>3</sup>(#3)b<sup>3</sup>7 or Eb<sup>4</sup>(#3)b<sup>3</sup>7.
47edo can be treated as a [[dual-fifth system]] in the 2.3+.3-.5.7.13 subgroup, or the 3+.3-.5.7.11+.11-.13 subgroup for those who aren’t intimidated by lots of [[basis element]]s. As a dual-fifth system, it really shines, as both of its fifths have low enough [[harmonic entropy]] to sound [[consonant]] to many listeners, giving two consonant intervals for the price of one.


Using the 2nd best 5th is even more awkward. The major 2nd is 9 edosteps and the minor is only one. The naturals create a 5edo-like scale, with two of the notes inflected by a comma-sized edostep:
=== Subsets and supersets ===
 
47edo is the 15th [[prime edo]], following [[43edo]] and preceding [[53edo]], so it does not contain any nontrivial subset edos, though it contains [[47ed4]]. [[94edo]], which doubles it, corrects its approximations of harmonics 3 and 11 to near-just qualities.
D * * * * * * * * E F * * * * * * * * G * * * * * * * * A * * * * * * * * B C * * * * * * * * D


D# is next to E. This notation requires quadruple, quintuple, and even sextuple ups and downs, as well as single sharps and flats.
=== Harmonics ===
{{Harmonics in equal|47}}
=== Subsets and supersets ===
47edo is the 15th [[prime EDO]], following [[43edo]] and preceding [[53edo]].
== Intervals ==
== Intervals ==
{| class="wikitable center-all right-2"
{| class="wikitable center-all right-2"
Line 30: Line 26:
|-
|-
| 0
| 0
| 0.0000
| 0.0
| perfect unison
| perfect unison
| P1
| P1
Line 36: Line 32:
|-
|-
| 1
| 1
| 25.5319
| 25.5
| aug 1sn
| aug 1sn
| A1
| A1
Line 42: Line 38:
|-
|-
| 2
| 2
| 51.0638
| 51.1
| double-aug 1sn
| double-aug 1sn
| AA1
| AA1
Line 48: Line 44:
|-
|-
| 3
| 3
| 76.5957
| 76.6
| triple-aug 1sn, triple-dim 2nd
| triple-aug 1sn, triple-dim 2nd
| A<sup>3</sup>1, d<sup>3</sup>2
| A<sup>3</sup>1, d<sup>3</sup>2
Line 54: Line 50:
|-
|-
| 4
| 4
| 102.1277
| 102.1
| double-dim 2nd
| double-dim 2nd
| dd2
| dd2
Line 60: Line 56:
|-
|-
| 5
| 5
| 127.6596
| 127.7
| dim 2nd
| dim 2nd
| d2
| d2
Line 66: Line 62:
|-
|-
| 6
| 6
| 153.1915
| 153.2
| minor 2nd
| minor 2nd
| m2
| m2
Line 72: Line 68:
|-
|-
| 7
| 7
| 178.7234
| 178.7
| major 2nd
| major 2nd
| M2
| M2
Line 78: Line 74:
|-
|-
| 8
| 8
| 204.2553
| 204.3
| aug 2nd
| aug 2nd
| A2
| A2
Line 84: Line 80:
|-
|-
| 9
| 9
| 229.7872
| 229.8
| double-aug 2nd
| double-aug 2nd
| AA2
| AA2
Line 90: Line 86:
|-
|-
| 10
| 10
| 255.3191
| 255.3
| triple-aug 2nd, triple-dim 3rd
| triple-aug 2nd, triple-dim 3rd
| A<sup>3</sup>2, d<sup>3</sup>3
| A<sup>3</sup>2, d<sup>3</sup>3
Line 96: Line 92:
|-
|-
| 11
| 11
| 280.8511
| 280.9
| double-dim 3rd
| double-dim 3rd
| dd3
| dd3
Line 102: Line 98:
|-
|-
| 12
| 12
| 306.3830
| 306.4
| dim 3rd
| dim 3rd
| d3
| d3
Line 108: Line 104:
|-
|-
| 13
| 13
| 331.9149
| 331.9
| minor 3rd
| minor 3rd
| m3
| m3
Line 114: Line 110:
|-
|-
| 14
| 14
| 357.4468
| 357.4
| major 3rd
| major 3rd
| M3
| M3
Line 120: Line 116:
|-
|-
| 15
| 15
| 382.9787
| 383.0
| aug 3rd
| aug 3rd
| A3
| A3
Line 126: Line 122:
|-
|-
| 16
| 16
| 408.5106
| 408.5
| double-aug 3rd
| double-aug 3rd
| AA3
| AA3
Line 132: Line 128:
|-
|-
| 17
| 17
| 434.0426
| 434.0
| triple-aug 3rd, triple-dim 4th
| triple-aug 3rd, triple-dim 4th
| A<sup>3</sup>3, d<sup>3</sup>4
| A<sup>3</sup>3, d<sup>3</sup>4
Line 138: Line 134:
|-
|-
| 18
| 18
| 459.5745
| 459.6
| double-dim 4th
| double-dim 4th
| dd4
| dd4
Line 144: Line 140:
|-
|-
| 19
| 19
| 485.1064
| 485.1
| dim 4th
| dim 4th
| d4
| d4
Line 150: Line 146:
|-
|-
| 20
| 20
| 510.6383
| 510.6
| perfect 4th
| perfect 4th
| P4
| P4
Line 156: Line 152:
|-
|-
| 21
| 21
| 536.1702
| 536.2
| aug 4th
| aug 4th
| A4
| A4
Line 162: Line 158:
|-
|-
| 22
| 22
| 561.7021
| 561.7
| double-aug 4th
| double-aug 4th
| AA4
| AA4
Line 168: Line 164:
|-
|-
| 23
| 23
| 587.2340
| 587.2
| triple-aug 4th
| triple-aug 4th
| A<sup>3</sup>4
| A<sup>3</sup>4
Line 174: Line 170:
|-
|-
| 24
| 24
| 612.7660
| 612.8
| triple-dim 5th
| triple-dim 5th
| d<sup>3</sup>5
| d<sup>3</sup>5
Line 180: Line 176:
|-
|-
| 25
| 25
| 638.2979
| 638.3
| double-dim 5th
| double-dim 5th
| dd5
| dd5
Line 186: Line 182:
|-
|-
| 26
| 26
| 663.8298
| 663.8
| dim 5th
| dim 5th
| d5
| d5
Line 192: Line 188:
|-
|-
| 27
| 27
| 689.3617
| 689.4
| perfect 5th
| perfect 5th
| P5
| P5
Line 198: Line 194:
|-
|-
| 28
| 28
| 714.8936
| 714.9
| aug 5th
| aug 5th
| A5
| A5
Line 204: Line 200:
|-
|-
| 29
| 29
| 740.4255
| 740.4
| double-aug 5th
| double-aug 5th
| AA5
| AA5
Line 210: Line 206:
|-
|-
| 30
| 30
| 765.9574
| 766.0
| triple-aug 5th, triple-dim 6th
| triple-aug 5th, triple-dim 6th
| A<sup>3</sup>5, d<sup>3</sup>6
| A<sup>3</sup>5, d<sup>3</sup>6
Line 216: Line 212:
|-
|-
| 31
| 31
| 791.4894
| 791.5
| double-dim 6th
| double-dim 6th
| dd6
| dd6
Line 222: Line 218:
|-
|-
| 32
| 32
| 817.0213
| 817.0
| dim 6th
| dim 6th
| d6
| d6
Line 228: Line 224:
|-
|-
| 33
| 33
| 842.5532
| 842.6
| minor 6th
| minor 6th
| m6
| m6
Line 234: Line 230:
|-
|-
| 34
| 34
| 868.0851
| 868.1
| major 6th
| major 6th
| M6
| M6
Line 240: Line 236:
|-
|-
| 35
| 35
| 893.6170
| 893.6
| aug 6th
| aug 6th
| A6
| A6
Line 246: Line 242:
|-
|-
| 36
| 36
| 919.1489
| 919.1
| double-aug 6th
| double-aug 6th
| AA6
| AA6
Line 252: Line 248:
|-
|-
| 37
| 37
| 944.6809
| 944.7
| triple-aug 6th, triple-dim 7th
| triple-aug 6th, triple-dim 7th
| A<sup>3</sup>6, d<sup>3</sup>7
| A<sup>3</sup>6, d<sup>3</sup>7
Line 258: Line 254:
|-
|-
| 38
| 38
| 970.2128
| 970.2
| double-dim 7th
| double-dim 7th
| dd7
| dd7
Line 264: Line 260:
|-
|-
| 39
| 39
| 995.7447
| 995.7
| dim 7th
| dim 7th
| d7
| d7
Line 270: Line 266:
|-
|-
| 40
| 40
| 1021.2766
| 1021.3
| minor 7th
| minor 7th
| m7
| m7
Line 276: Line 272:
|-
|-
| 41
| 41
| 1046.8085
| 1046.8
| major 7th
| major 7th
| M7
| M7
Line 282: Line 278:
|-
|-
| 42
| 42
| 1072.3404
| 1072.3
| aug 7th
| aug 7th
| A7
| A7
Line 288: Line 284:
|-
|-
| 43
| 43
| 1097.8723
| 1097.9
| double-aug 7th
| double-aug 7th
| AA7
| AA7
Line 294: Line 290:
|-
|-
| 44
| 44
| 1123.4043
| 1123.4
| triple-aug 7th, triple-dim 8ve
| triple-aug 7th, triple-dim 8ve
| A<sup>3</sup>7, d<sup>3</sup>8
| A<sup>3</sup>7, d<sup>3</sup>8
Line 300: Line 296:
|-
|-
| 45
| 45
| 1148.9362
| 1148.9
| double-dim 8ve
| double-dim 8ve
| dd8
| dd8
Line 306: Line 302:
|-
|-
| 46
| 46
| 1174.4681
| 1174.5
| dim 8ve
| dim 8ve
| d8
| d8
Line 312: Line 308:
|-
|-
| 47
| 47
| 1200.0000
| 1200.0
| perfect 8ve
| perfect 8ve
| P8
| P8
| D
| D
|}
|}
== Notation ==
A notation using the best 5th has major and minor 2nds of 7 and 6 edosteps respectively, with the naturals creating a 7edo-like scale:
D * * * * * * E * * * * * F * * * * * * G * * * * * * A * * * * * * B * * * * * C * * * * * * D
D# is next to D. This notation requires triple, quadruple and in some keys, quintuple or more sharps and flats. For example, a 0-15-27-38 chord (an approximate 4:5:6:7) on the note three edosteps above D would be spelled either as D#<sup>3</sup> - F#<sup>5</sup> - A#<sup>3</sup> - C# or as Eb<sup>4</sup> - Gbb - Ab<sup>4</sup> - Db<sup>6</sup>. This is an aug-three double-dim-seven chord, written D#<sup>3</sup>(A3)dd7 or Eb<sup>4</sup>(A3)dd7. It could also be called a sharp-three triple-flat-seven chord, written D#<sup>3</sup>(#3)b<sup>3</sup>7 or Eb<sup>4</sup>(#3)b<sup>3</sup>7.
Using the 2nd best 5th is even more awkward. The major 2nd is 9 edosteps and the minor is only one. The naturals create a 5edo-like scale, with two of the notes inflected by a comma-sized edostep:
D * * * * * * * * E F * * * * * * * * G * * * * * * * * A * * * * * * * * B C * * * * * * * * D
D# is next to E. This notation requires quadruple, quintuple, and even sextuple ups and downs, as well as single sharps and flats.
=== Ups and downs notation ===
Using [[Helmholtz–Ellis]] accidentals and the sharp fifth, 47edo can be notated using [[ups and downs notation|ups and downs]]:
{{Sharpness-sharp8}}
With the flat fifth, notation is identical to standard notation:
{{Sharpness-sharp1}}
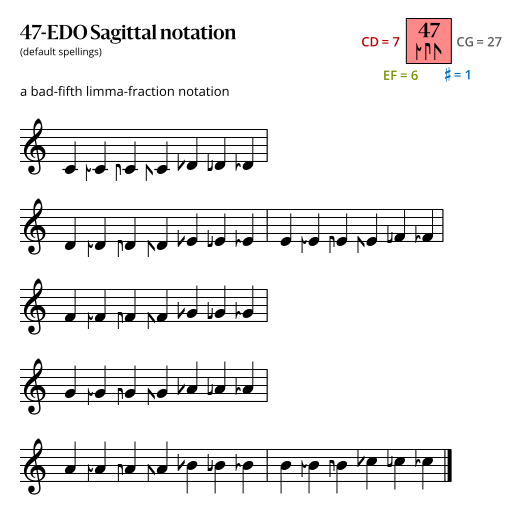
=== Sagittal notation ===
==== Best fifth notation ====
This notation uses the same sagittal sequence as [[42edo#Second-best fifth notation|42b]].
<imagemap>
File:47-EDO_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 519 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 300 106 [[Fractional_3-limit_notation#Bad-fifths_limma-fraction_notation | limma-fraction notation]]
default [[File:47-EDO_Sagittal.svg]]
</imagemap>
==== Second-best fifth notation ====
===== Evo and Revo flavors =====
<imagemap>
File:47b_Sagittal.svg
desc none
rect 80 0 280 50 [[Sagittal_notation]]
rect 280 0 440 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 300 106 [[Fractional_3-limit_notation#Bad-fifths_apotome-fraction_notation | apotome-fraction notation]]
default [[File:47b_Sagittal.svg]]
</imagemap>
===== Alternative Evo flavor =====
<imagemap>
File:47b_Alternative_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 389 0 549 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 389 106 [[Fractional_3-limit_notation#Bad-fifths_apotome-fraction_notation | apotome-fraction notation]]
default [[File:47b_Alternative_Evo_Sagittal.svg]]
</imagemap>
===== Evo-SZ flavor =====
<imagemap>
File:47b_Evo-SZ_Sagittal.svg
desc none
rect 80 0 335 50 [[Sagittal_notation]]
rect 335 0 495 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 300 106 [[Fractional_3-limit_notation#Bad-fifths_apotome-fraction_notation | apotome-fraction notation]]
default [[File:47b_Evo-SZ_Sagittal.svg]]
</imagemap>


== Scales ==
== Scales ==
* [[Negri in zeta-stretched 47edo]]
* [[Negri in zeta-stretched 47edo]]
* Quasi-equal [[equiheptatonic]] (Dorian): 7 6 7 7 7 6 7
** Quasi-equiheptatonic minor pentatonic: 13 7 7 13 7
* Quasi-equal [[equiheptatonic]] (Mixolydian): 7 7 6 7 7 6 7
* Quasi-equal [[equipentatonic]]: 9 10 9 10 9
* Sabertooth hexatonic: 3 9 3 13 12 7 (this is the original/default tuning; [[scalesmith|designed]] for the "gold" and "platinum" timbres in [[Scale Workshop]])
** Sabertooth pentatonic: 3 9 3 13 19 (this is the original/default tuning)
** Sabertooth neutral: 3 11 14 11 8 (this is the original/default tuning)


== Instrument mappings ==
== Instruments ==
=== Lumatone ===
* [[Lumatone mapping for 47edo]]
* [[Lumatone mapping for 47edo]]
=== Skip fretting ===
'''Skip fretting system 47 3 11''' is a [[skip-fretting]] system for [[47edo]] where strings are 11\47 and frets are 3\47. This is effectively 15.6666...-edo. All examples of this system on this page are for 5-string bass.
; Chords
Neutral-dominant 7th: 1 0 1 2 2
== Music ==
* [https://youtu.be/_TqaWw7tv_E Improvisation in 47edo (octave-compressed tuning, 7-note subset of Negri[9<nowiki>]</nowiki>)] by [[Budjarn Lambeth]], Jan 2024
[[Category:Listen]]
[[Category:Todo:add rank 2 temperaments table]]

Latest revision as of 03:53, 27 April 2025

← 46edo 47edo 48edo →
Prime factorization 47 (prime)
Step size 25.5319 ¢ 
Fifth 27\47 (689.362 ¢)
Semitones (A1:m2) 1:6 (25.53 ¢ : 153.2 ¢)
Dual sharp fifth 28\47 (714.894 ¢)
Dual flat fifth 27\47 (689.362 ¢)
Dual major 2nd 8\47 (204.255 ¢)
(convergent)
Consistency limit 5
Distinct consistency limit 5

47 equal divisions of the octave (abbreviated 47edo or 47ed2), also called 47-tone equal temperament (47tet) or 47 equal temperament (47et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 47 equal parts of about 25.5 ¢ each. Each step represents a frequency ratio of 21/47, or the 47th root of 2.

Theory

47edo is the first edo that has two diatonic perfect fifths, as both fall between 4\7 = 686 ¢ and 3\5 = 720 ¢. The fifth closest to 3/2 is 12.593-cent flat, unless you use the alternative fifth which is 12.939-cent sharp, similar to 35edo. The soft diatonic scale generated from its flat fifth is so soft, with L:s = 7:6, that it stops sounding like meantone or even a flattone system like 26edo or 40edo, but just sounds like a circulating temperament of 7edo. The hard diatonic scale generated from its sharp fifth is extremely hard, with L:s = 9:1. It has therefore not aroused much interest, but its best approximation to 9/8 is actually quite good, one-third-of-a-cent sharp.

47edo is one of the most difficult diatonic edos to notate in native fifths, because no other diatonic edo's fifth is as extreme.

Odd harmonics

Approximation of odd harmonics in 47edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) -12.6 -3.3 +1.4 +0.3 +10.4 +2.0 +9.6 -2.8 +8.9 -11.2 +10.0
Relative (%) -49.3 -13.1 +5.4 +1.4 +40.7 +7.9 +37.6 -11.1 +34.7 -43.9 +39.3
Steps
(reduced) 		74
(27) 		109
(15) 		132
(38) 		149
(8) 		163
(22) 		174
(33) 		184
(43) 		192
(4) 		200
(12) 		206
(18) 		213
(25)

47edo does a good job of approximating the 2.9.5.7.33.13.17.57.69 23-limit 2*47 subgroup of the 23-limit, on which it tempers out the same commas as 94edo. It provides a good tuning for baldy and silver and their relatives. It also provides a good tuning for the baseball temperament.

47edo can be treated as a dual-fifth system in the 2.3+.3-.5.7.13 subgroup, or the 3+.3-.5.7.11+.11-.13 subgroup for those who aren’t intimidated by lots of basis elements. As a dual-fifth system, it really shines, as both of its fifths have low enough harmonic entropy to sound consonant to many listeners, giving two consonant intervals for the price of one.

Subsets and supersets

47edo is the 15th prime edo, following 43edo and preceding 53edo, so it does not contain any nontrivial subset edos, though it contains 47ed4. 94edo, which doubles it, corrects its approximations of harmonics 3 and 11 to near-just qualities.

Intervals

# Cents Relative notation Absolute notation
0 0.0 perfect unison P1 D
1 25.5 aug 1sn A1 D#
2 51.1 double-aug 1sn AA1 Dx
3 76.6 triple-aug 1sn, triple-dim 2nd A31, d32 D#3, Eb4
4 102.1 double-dim 2nd dd2 Eb3
5 127.7 dim 2nd d2 Ebb
6 153.2 minor 2nd m2 Eb
7 178.7 major 2nd M2 E
8 204.3 aug 2nd A2 E#
9 229.8 double-aug 2nd AA2 Ex
10 255.3 triple-aug 2nd, triple-dim 3rd A32, d33 E#3, Fb3
11 280.9 double-dim 3rd dd3 Fbb
12 306.4 dim 3rd d3 Fb
13 331.9 minor 3rd m3 F
14 357.4 major 3rd M3 F#
15 383.0 aug 3rd A3 Fx
16 408.5 double-aug 3rd AA3 F#3
17 434.0 triple-aug 3rd, triple-dim 4th A33, d34 F#4, Gb3
18 459.6 double-dim 4th dd4 Gbb
19 485.1 dim 4th d4 Gb
20 510.6 perfect 4th P4 G
21 536.2 aug 4th A4 G#
22 561.7 double-aug 4th AA4 Gx
23 587.2 triple-aug 4th A34 G#3
24 612.8 triple-dim 5th d35 Ab3
25 638.3 double-dim 5th dd5 Abb
26 663.8 dim 5th d5 Ab
27 689.4 perfect 5th P5 A
28 714.9 aug 5th A5 A#
29 740.4 double-aug 5th AA5 Ax
30 766.0 triple-aug 5th, triple-dim 6th A35, d36 A#3, Bb4
31 791.5 double-dim 6th dd6 Bb3
32 817.0 dim 6th d6 Bbb
33 842.6 minor 6th m6 Bb
34 868.1 major 6th M6 B
35 893.6 aug 6th A6 B#
36 919.1 double-aug 6th AA6 Bx
37 944.7 triple-aug 6th, triple-dim 7th A36, d37 B#3, Cb3
38 970.2 double-dim 7th dd7 Cbb
39 995.7 dim 7th d7 Cb
40 1021.3 minor 7th m7 C
41 1046.8 major 7th M7 C#
42 1072.3 aug 7th A7 Cx
43 1097.9 double-aug 7th AA7 C#3
44 1123.4 triple-aug 7th, triple-dim 8ve A37, d38 C#4, Db3
45 1148.9 double-dim 8ve dd8 Dbb
46 1174.5 dim 8ve d8 Db
47 1200.0 perfect 8ve P8 D

Notation

A notation using the best 5th has major and minor 2nds of 7 and 6 edosteps respectively, with the naturals creating a 7edo-like scale:

D * * * * * * E * * * * * F * * * * * * G * * * * * * A * * * * * * B * * * * * C * * * * * * D

D# is next to D. This notation requires triple, quadruple and in some keys, quintuple or more sharps and flats. For example, a 0-15-27-38 chord (an approximate 4:5:6:7) on the note three edosteps above D would be spelled either as D#3 - F#5 - A#3 - C# or as Eb4 - Gbb - Ab4 - Db6. This is an aug-three double-dim-seven chord, written D#3(A3)dd7 or Eb4(A3)dd7. It could also be called a sharp-three triple-flat-seven chord, written D#3(#3)b37 or Eb4(#3)b37.

Using the 2nd best 5th is even more awkward. The major 2nd is 9 edosteps and the minor is only one. The naturals create a 5edo-like scale, with two of the notes inflected by a comma-sized edostep:

D * * * * * * * * E F * * * * * * * * G * * * * * * * * A * * * * * * * * B C * * * * * * * * D

D# is next to E. This notation requires quadruple, quintuple, and even sextuple ups and downs, as well as single sharps and flats.

Ups and downs notation

Using Helmholtz–Ellis accidentals and the sharp fifth, 47edo can be notated using ups and downs:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Sharp symbol  
Flat symbol

With the flat fifth, notation is identical to standard notation:

Step offset −2 −1 0 +1 +2
Symbol  
 		 
 		 
 		 
 		 

Sagittal notation

Best fifth notation

This notation uses the same sagittal sequence as 42b.

Sagittal notationPeriodic table of EDOs with sagittal notationlimma-fraction notation

Second-best fifth notation

Evo and Revo flavors
Sagittal notationPeriodic table of EDOs with sagittal notationapotome-fraction notation
Alternative Evo flavor
Sagittal notationPeriodic table of EDOs with sagittal notationapotome-fraction notation
Evo-SZ flavor
Sagittal notationPeriodic table of EDOs with sagittal notationapotome-fraction notation

Scales

  • Negri in zeta-stretched 47edo
  • Quasi-equal equiheptatonic (Dorian): 7 6 7 7 7 6 7
    • Quasi-equiheptatonic minor pentatonic: 13 7 7 13 7
  • Quasi-equal equiheptatonic (Mixolydian): 7 7 6 7 7 6 7
  • Quasi-equal equipentatonic: 9 10 9 10 9
  • Sabertooth hexatonic: 3 9 3 13 12 7 (this is the original/default tuning; designed for the "gold" and "platinum" timbres in Scale Workshop)
    • Sabertooth pentatonic: 3 9 3 13 19 (this is the original/default tuning)
    • Sabertooth neutral: 3 11 14 11 8 (this is the original/default tuning)

Instruments

Lumatone

Skip fretting

Skip fretting system 47 3 11 is a skip-fretting system for 47edo where strings are 11\47 and frets are 3\47. This is effectively 15.6666...-edo. All examples of this system on this page are for 5-string bass.

Chords

Neutral-dominant 7th: 1 0 1 2 2

Music

Retrieved from "https://en.xen.wiki/index.php?title=47edo&oldid=194216"