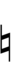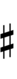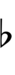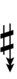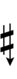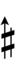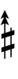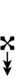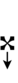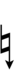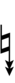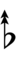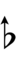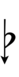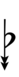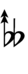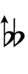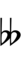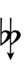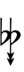81edo: Difference between revisions

← Older edit

VisualWikitext

Latest revision as of 07:43, 14 July 2025

← 80edo

81edo

82edo →

Prime factorization

3⁴

Step size

14.8148 ¢

Fifth

47\81 (696.296 ¢)

Semitones (A1:m2)

5:8 (74.07 ¢ : 118.5 ¢)

Dual sharp fifth

48\81 (711.111 ¢) (→ 16\27)

Dual flat fifth

47\81 (696.296 ¢)

Dual major 2nd

14\81 (207.407 ¢)

Consistency limit

7

Distinct consistency limit

7

81 equal divisions of the octave (abbreviated 81edo or 81ed2), also called 81-tone equal temperament (81tet) or 81 equal temperament (81et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 81 equal parts of about 14.8 ¢ each. Each step represents a frequency ratio of 2^1/81, or the 81st root of 2.

Theory

81edo is notable as a tuning for meantone and related temperaments and is the optimal patent val for a number of them. In particular it is the optimal patent val for 5-limit meantone, 7-limit meantone, 11-limit meanpop, 13-limit meanpop, and the rank-3 temperament erato. The electronic music pioneer Daphne Oram was interested in 81edo^[1]. As a step in the Golden meantone series of edos, 81edo marks the point at which the series ceases to display audible changes to meantone temperament, and is also the edo with the lowest average and most evenly spread Just-error across the scale (though 31edo does have the best harmonic 7th). However, it is no longer consistent in the 9-odd-limit, as the best direct approximations of 9/8 and 10/9 are one step above and below the patent val mapping.

Besides meantone, 81edo is a tuning for the cobalt temperament, since 81 contains 27 as a divisor. It also tunes the unnamed 15 & 51 temperament which divides the octave into 3 equal parts, and is a member of the augmented-cloudy equivalence continuum. The 81bd val is a tuning for the septimal porcupine temperament.

In the higher limits, it is a strong tuning for the 2.5.17.19 subgroup, and also can be used to map 19/17 to the meantone major second resulting from stacking of two patent val fifths (13\81).

Odd harmonics

Approximation of odd harmonics in 81edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	-5.66	-1.13	-5.86	+3.50	-3.17	+3.92	-6.79	-1.25	-1.22	+3.29	-6.05
Error	Relative (%)	-38.2	-7.6	-39.6	+23.6	-21.4	+26.4	-45.8	-8.4	-8.2	+22.2	-40.9
Steps (reduced)		128 (47)	188 (26)	227 (65)	257 (14)	280 (37)	300 (57)	316 (73)	331 (7)	344 (20)	356 (32)	366 (42)

Subsets and supersets

Since 81 is equal to 3⁴, a perfect power of 3, 81edo contains subset edos 3, 9, and 27.

Intervals

Steps	Cents	Approximate ratios	Ups and downs notation (Dual flat fifth 47\81)	Ups and downs notation (Dual sharp fifth 48\81)
0	0	1/1	D	D
1	14.8		^D, vvE♭♭	^D, vvE♭
2	29.6		^^D, vE♭♭	^^D, vE♭
3	44.4	38/37, 39/38, 40/39	vvD♯, E♭♭	^³D, E♭
4	59.3	29/28, 30/29, 31/30	vD♯, ^E♭♭	^⁴D, ^E♭
5	74.1	23/22, 24/23	D♯, ^^E♭♭	^⁵D, ^^E♭
6	88.9	20/19, 39/37	^D♯, vvE♭	^⁶D, ^³E♭
7	103.7	17/16, 35/33	^^D♯, vE♭	v⁵D♯, ^⁴E♭
8	118.5	15/14, 31/29	vvD𝄪, E♭	v⁴D♯, ^⁵E♭
9	133.3	40/37	vD𝄪, ^E♭	v³D♯, v⁶E
10	148.1	12/11, 37/34	D𝄪, ^^E♭	vvD♯, v⁵E
11	163	11/10, 34/31	^D𝄪, vvE	vD♯, v⁴E
12	177.8	31/28	^^D𝄪, vE	D♯, v³E
13	192.6	19/17	E	^D♯, vvE
14	207.4	35/31	^E, vvF♭	^^D♯, vE
15	222.2	25/22, 33/29	^^E, vF♭	E
16	237	39/34	vvE♯, F♭	^E, vvF
17	251.9	22/19, 37/32	vE♯, ^F♭	^^E, vF
18	266.7	7/6	E♯, ^^F♭	F
19	281.5	20/17, 33/28	^E♯, vvF	^F, vvG♭
20	296.3	19/16	^^E♯, vF	^^F, vG♭
21	311.1		F	^³F, G♭
22	325.9	29/24, 35/29	^F, vvG♭♭	^⁴F, ^G♭
23	340.7	28/23, 39/32	^^F, vG♭♭	^⁵F, ^^G♭
24	355.6	38/31	vvF♯, G♭♭	^⁶F, ^³G♭
25	370.4	31/25	vF♯, ^G♭♭	v⁵F♯, ^⁴G♭
26	385.2	5/4	F♯, ^^G♭♭	v⁴F♯, ^⁵G♭
27	400	29/23, 39/31	^F♯, vvG♭	v³F♯, v⁶G
28	414.8	14/11	^^F♯, vG♭	vvF♯, v⁵G
29	429.6	32/25	vvF𝄪, G♭	vF♯, v⁴G
30	444.4	22/17, 31/24, 40/31	vF𝄪, ^G♭	F♯, v³G
31	459.3	30/23	F𝄪, ^^G♭	^F♯, vvG
32	474.1	25/19	^F𝄪, vvG	^^F♯, vG
33	488.9		^^F𝄪, vG	G
34	503.7		G	^G, vvA♭
35	518.5	31/23	^G, vvA♭♭	^^G, vA♭
36	533.3	34/25	^^G, vA♭♭	^³G, A♭
37	548.1	11/8	vvG♯, A♭♭	^⁴G, ^A♭
38	563		vG♯, ^A♭♭	^⁵G, ^^A♭
39	577.8		G♯, ^^A♭♭	^⁶G, ^³A♭
40	592.6	31/22	^G♯, vvA♭	v⁵G♯, ^⁴A♭
41	607.4		^^G♯, vA♭	v⁴G♯, ^⁵A♭
42	622.2	33/23	vvG𝄪, A♭	v³G♯, v⁶A
43	637		vG𝄪, ^A♭	vvG♯, v⁵A
44	651.9	16/11, 35/24	G𝄪, ^^A♭	vG♯, v⁴A
45	666.7	25/17	^G𝄪, vvA	G♯, v³A
46	681.5	37/25	^^G𝄪, vA	^G♯, vvA
47	696.3		A	^^G♯, vA
48	711.1		^A, vvB♭♭	A
49	725.9	35/23, 38/25	^^A, vB♭♭	^A, vvB♭
50	740.7	23/15	vvA♯, B♭♭	^^A, vB♭
51	755.6	17/11, 31/20	vA♯, ^B♭♭	^³A, B♭
52	770.4	25/16, 39/25	A♯, ^^B♭♭	^⁴A, ^B♭
53	785.2	11/7	^A♯, vvB♭	^⁵A, ^^B♭
54	800		^^A♯, vB♭	^⁶A, ^³B♭
55	814.8	8/5	vvA𝄪, B♭	v⁵A♯, ^⁴B♭
56	829.6		vA𝄪, ^B♭	v⁴A♯, ^⁵B♭
57	844.4	31/19	A𝄪, ^^B♭	v³A♯, v⁶B
58	859.3	23/14	^A𝄪, vvB	vvA♯, v⁵B
59	874.1		^^A𝄪, vB	vA♯, v⁴B
60	888.9		B	A♯, v³B
61	903.7	32/19	^B, vvC♭	^A♯, vvB
62	918.5	17/10	^^B, vC♭	^^A♯, vB
63	933.3	12/7	vvB♯, C♭	B
64	948.1	19/11	vB♯, ^C♭	^B, vvC
65	963		B♯, ^^C♭	^^B, vC
66	977.8		^B♯, vvC	C
67	992.6	39/22	^^B♯, vC	^C, vvD♭
68	1007.4	34/19	C	^^C, vD♭
69	1022.2		^C, vvD♭♭	^³C, D♭
70	1037	20/11, 31/17	^^C, vD♭♭	^⁴C, ^D♭
71	1051.9	11/6	vvC♯, D♭♭	^⁵C, ^^D♭
72	1066.7	37/20	vC♯, ^D♭♭	^⁶C, ^³D♭
73	1081.5	28/15	C♯, ^^D♭♭	v⁵C♯, ^⁴D♭
74	1096.3	32/17	^C♯, vvD♭	v⁴C♯, ^⁵D♭
75	1111.1	19/10	^^C♯, vD♭	v³C♯, v⁶D
76	1125.9	23/12	vvC𝄪, D♭	vvC♯, v⁵D
77	1140.7	29/15	vC𝄪, ^D♭	vC♯, v⁴D
78	1155.6	37/19, 39/20	C𝄪, ^^D♭	C♯, v³D
79	1170.4		^C𝄪, vvD	^C♯, vvD
80	1185.2		^^C𝄪, vD	^^C♯, vD
81	1200	2/1	D	D

Notation

Ups and downs notation

81edo can be notated with ups and downs, spoken as up, dup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, dupflat etc. Note that dudsharp is equivalent to trup (triple-up) and dupflat is equivalent to trud (triple-down).

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12
Sharp symbol
Flat symbol

Another notation uses alternative ups and downs. Here, this can be done using sharps and flats with arrows, borrowed from extended Helmholtz–Ellis notation:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12
Sharp symbol
Flat symbol

Tom Winspear's notation

81edo accidentals created and used by Tom Winspear, based on those provided in Scala though with a logic correction. The innermost accidentals represent one edostep, followed by two, then the bracket representing three. What appears to be a half-sharp is actually a fifth-sharp. Conventional sharp/doublesharp/flat/doubleflat accidentals are reached in steps of five and the pattern repeats itself on them. The chromatic scale can be notated utilizing only six accidentals in either direction—the rest are for enharmonics.

Regular temperament properties

Commas

5-limit commas: 81/80, [-48 1 20⟩
7-limit commas: 81/80, 126/125, [-24 1 0 8⟩
11-limit commas: 81/80, 126/125, 385/384, 12005/11979
13-limit commas: 81/80, 105/104, 144/143, 196/195, 6655/6591

Scales

Instruments

Skip fretting

Skip fretting system 81 7 20 is a skip fretting system for 81edo. All examples on this page are for 7-string guitar.

Prime harmonics

1/1: string 2 open

2/1: string 5 fret 3

3/2: string 4 fret 1 and string 7 fret 4

5/4: string 7 fret 1

7/4: string 3 fret 18

11/8: string 3 fret 14

13/8: string 1 fret 11 and string 4 fret 14

17/16: string 2 fret 1 and string 5 fret 4

19/16: string 3 open

23/16: string 2 fret 6 and string 5 fret 9

29/16: string 3 fret 7 and string 6 fret 10

31/16: string 2 fret 11 and string 5 fret 14

Chords

Minor 7th: 100133x

Dominant 7th: 10113xx

Keyboards

A Lumatone mapping for 81edo is available.

Music

Bryan Deister

''microtonal improvisation in 81edo (2025)

Notes

↑ Letter from Yehudi Menuhin to Daphne Oram

[1] Letter from Yehudi Menuhin to Daphne Oram

[1]

@@ Line 1: / Line 1: @@
+{{Infobox ET}}
+{{ED intro}}
+== Theory ==
 [[File:81 EDO structure-accidentals-notation-colour notation.png|thumb|
-By [[Tom Winspear]], utilizing the Accidents shown below. Left: Chain of 4ths/5ths , Right: Chromatic view. Black font represents the '6 accidentals deep' notation that covers the chromatic scale with enharmonics only across EF & BC. White text displays deep enharmonics in the ambiguous infrared & ultraviolet area of the colour notation.
+By [[Tom Winspear]], utilizing the Accidents shown below. Left: Chain of 4ths/5ths, Right: Chromatic view. Black font represents the '6 accidentals deep' notation that covers the chromatic scale with enharmonics only across EF & BC. White text displays deep enharmonics in the ambiguous infrared & ultraviolet area of the colour notation.
 ]]
-'''81edo''' divides the octave into 81 steps of 14.815 [[cent]]s each. It is notable as a tuning for [[meantone family|meantone]] and related temperaments and is the [[optimal patent val]] for a number of them. In particular it is the optimal patent val for 5-limit meantone, 7-limit meantone, 11-limit meanpop, 13-limit meanpop, and the rank three temperament [[Didymus rank three family|erato]]. The electronic music pioneer [https://web.archive.org/web/20120211182601/http://daphneoram.org/2012/01/13/letter-from-yehudi-menuhin/ Daphne Oram] was interested in 81edo.
-As a step in the [[Golden meantone]] series of EDOs, 81 EDO marks the point at which the series ceases to display audible changes to meantone temperament, and is also the EDO with the lowest average and most evenly spread Just-error across the scale (though 31 EDO does have the best harmonic 7th).
+edo is notable as a tuning for [[meantone family|meantone]] and related temperaments and is the [[optimal patent val]] for a number of them. In particular it is the optimal patent val for 5-limit meantone, 7-limit meantone, 11-limit meanpop, 13-limit meanpop, and the rank-3 temperament [[erato]]. The electronic music pioneer {{w|Daphne Oram}} was interested in 81edo<ref>[https://web.archive.org/web/20120211182601/http://daphneoram.org/2012/01/13/letter-from-yehudi-menuhin/ Letter from Yehudi Menuhin to Daphne Oram]</ref>. As a step in the [[Golden meantone]] series of edos, 81edo marks the point at which the series ceases to display audible changes to meantone temperament, and is also the edo with the lowest average and most evenly spread Just-error across the scale (though 31edo does have the best [[7/4|harmonic 7th]]). However, it is no longer [[consistent]] in the [[9-odd-limit]], as the best direct approximations of [[9/8]] and [[10/9]] are one step above and below the patent val mapping.
+Besides meantone, 81edo is a tuning for the [[cobalt]] temperament, since 81 contains 27 as a divisor. It also tunes the unnamed 15 & 51 temperament which divides the octave into 3 equal parts, and is a member of the [[augmented-cloudy equivalence continuum]]. The 81bd val is a tuning for the [[Porcupine family#Septimal porcupine|septimal porcupine]] temperament.
+In the higher limits, it is a strong tuning for the 2.5.17.19 subgroup, and also can be used to map [[19/17]] to the meantone major second resulting from stacking of two patent val fifths (13\81).
-[[File:81 EDO Accidentals.png|thumb|
+=== Odd harmonics ===
-EDO Accidentals created and used by Tom Winspear.
+{{Harmonics in equal|81}}
-Based on those provided in Scala though with a logic correction.
-The innermost accidentals represent the 15 cent EDOstep, followed by two, then the bracket representing three. Conventional sharp/doublesharp/flat/doubleflat accidentals are reached in steps of five and the pattern repeats itself on them.
+=== Subsets and supersets ===
-The chromatic scale can be notated utilizing only six accidentals in either direction - the rest are for enharmonics.
+Since 81 is equal to 3<sup>4</sup>, a perfect power of 3, 81edo contains subset edos {{EDOs| 3, 9, and 27 }}.
-]]
+== Intervals ==
+{{Interval table}}
+== Notation ==
+===Ups and downs notation===
+edo can be notated with [[ups and downs]], spoken as up, dup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, dupflat etc. Note that dudsharp is equivalent to trup (triple-up) and dupflat is equivalent to trud (triple-down).
+{{Sharpness-sharp5a}}
+Another notation uses [[Alternative symbols for ups and downs notation#Sharp-5|alternative ups and downs]]. Here, this can be done using sharps and flats with arrows, borrowed from extended [[Helmholtz–Ellis notation]]:
+{{Sharpness-sharp5}}
+=== Tom Winspear's notation ===
+[[File:81 EDO Accidentals.png|alt=|959x959px]]
-== Commas ==
+edo accidentals created and used by [[Tom Winspear]], based on those provided in [[Scala]] though with a logic correction. The innermost accidentals represent one edostep, followed by two, then the bracket representing three. What appears to be a half-sharp is actually a fifth-sharp. Conventional sharp/doublesharp/flat/doubleflat accidentals are reached in steps of five and the pattern repeats itself on them. The chromatic scale can be notated utilizing only six accidentals in either direction—the rest are for enharmonics.
-* 5-limit commas: 81/80, |-48 1 20&gt;
+== Regular temperament properties ==
-* 7-limit commas: 81/80, 126/125, |-24 1 0 8&gt;
+=== Commas ===
+* 5-limit commas: 81/80, {{monzo|-48 1 20}}
+* 7-limit commas: 81/80, 126/125, {{monzo|-24 1 0 8}}
 * 11-limit commas: 81/80, 126/125, 385/384, 12005/11979
 * 13-limit commas: 81/80, 105/104, 144/143, 196/195, 6655/6591
 == Scales ==
+* [[Leantone6]]
+* [[Leantone7]]
+* [[Leantone13]]
+== Instruments ==
+=== Skip fretting ===
+'''Skip fretting system 81 7 20''' is a [[skip fretting]] system for [[81edo]]. All examples on this page are for 7-string [[guitar]].
+; Prime harmonics
+/1: string 2 open
+/1: string 5 fret 3
+/2: string 4 fret 1 and string 7 fret 4
+/4: string 7 fret 1
+/4: string 3 fret 18
+/8: string 3 fret 14
+/8: string 1 fret 11 and string 4 fret 14
+/16: string 2 fret 1 and string 5 fret 4
+/16: string 3 open
+/16: string 2 fret 6 and string 5 fret 9
+/16: string 3 fret 7 and string 6 fret 10
+/16: string 2 fret 11 and string 5 fret 14
+; Chords
+Minor 7th: 100133x
+Dominant 7th: 10113xx
+=== Keyboards ===
+A [[Lumatone mapping for 81edo]] is available.
+== Music ==
+; [[Bryan Deister]]
+* [https://www.youtube.com/shorts/5O6Cyawjkd8 ''''microtonal improvisation in 81edo''] (2025)
-* [[leantone6|leantone6]]
+== Notes ==
-* [[leantone7|leantone7]]
-* [[leantone13|leantone13]]
-[[Category:Theory]]
-[[Category:81edo]]
-[[Category:Equal divisions of the octave]]
 [[Category:Erato]]
+[[Category:Golden meantone]]
+[[Category:Leantone]]
 [[Category:Meantone]]
 [[Category:Meanpop]]
+<references />

81edo: Difference between revisions

Latest revision as of 07:43, 14 July 2025

Contents