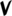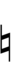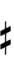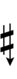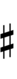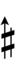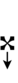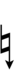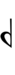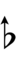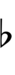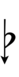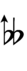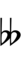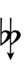76edo: Difference between revisions
Wikispaces>MasonGreen1 **Imported revision 596770372 - Original comment: ** |
→Instruments: Lumatone mappings for 76edo are now available |
||
| (23 intermediate revisions by 14 users not shown) | |||
| Line 1: | Line 1: | ||
{{Infobox ET}} | |||
{{ED intro}} | |||
== Theory == | |||
76edo's [[patent val]] is [[contorted]] in the 5-limit, reflecting the fact that {{nowrap|76 {{=}} 4 × 19}}. In the 7-limit it [[tempering out|tempers out]] [[2401/2400]] in addition to [[81/80]], and so [[support]]s the [[squares]] temperament. In the 11-limit, it tempers out [[245/242]] and [[385/384]], and supports [[pombe]], the {{nowrap|24 & 26}} temperament. In the 13-limit, it tempers out 105/104, 144/143, 351/350 and 364/363. While the {{nowrap|44\76 {{=}} 11\19}} fifth is already flat, the 43\76 fifth, even flatter, is an almost perfect approximation to the [[hornbostel]] temperament's [[POTE]] fifth, whereas its sharp fifth, 45\76, makes for an excellent [[superpyth]] fifth. Hence you can do hornbostel/mavila, squares/meantone, and superpyth all with the same equal division. | |||
Using the 76dgh val, 76edo provides an excellent tuning for [[teff]] temperament, a low-complexity, medium-accuracy, and high-limit (17- or 19-limit) temperament. | |||
Using | |||
=== Odd harmonics === | |||
{{Harmonics in equal|76}} | |||
=== Subsets and supersets === | |||
Since 76 factors into {{factorization|76}}, 76edo has subset edos {{EDOs| 2, 4, 19, and 38 }}. [[152edo]], which doubles it, is a [[zeta peak edo]]. | |||
== Intervals == | |||
{{Interval table}} | |||
== Notation == | |||
=== Ups and downs notation === | |||
76edo can be notated with [[ups and downs]], spoken as up, dup, downsharp, sharp, upsharp etc. and down, dud, upflat etc. Note that dup is equivalent to dudsharp and dud is equivalent to dupflat. | |||
{{Sharpness-sharp4a}} | |||
Using [[Helmholtz–Ellis]] accidentals, 76edo can also be notated using [[ups and downs notation]] along with Stein–Zimmerman [[24edo#Notation|quarter-tone]] accidentals: | |||
{{Sharpness-sharp4}} | |||
Here, a sharp raises by four steps, and a flat lowers by four steps, so arrows can be used to fill in the gap. | |||
=== Sagittal notation === | |||
This notation uses the same sagittal sequence as EDOs [[62edo#Sagittal notation|62]] and [[69edo#Sagittal notation|69]], and is a superset of the notations for EDOs [[38edo#Sagittal notation|38]] and [[19edo#Sagittal notation|19]]. | |||
==== Evo flavor ==== | |||
<imagemap> | |||
File:76-EDO_Evo_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 575 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 170 106 [[1053/1024]] | |||
rect 170 80 330 106 [[567/550]] | |||
default [[File:76-EDO_Evo_Sagittal.svg]] | |||
</imagemap> | |||
==== Revo flavor ==== | |||
<imagemap> | |||
File:76-EDO_Revo_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 604 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 170 106 [[1053/1024]] | |||
rect 170 80 330 106 [[567/550]] | |||
default [[File:76-EDO_Revo_Sagittal.svg]] | |||
</imagemap> | |||
==== Evo-SZ flavor ==== | |||
<imagemap> | |||
File:76-EDO_Evo-SZ_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 553 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 170 106 [[1053/1024]] | |||
rect 170 80 330 106 [[567/550]] | |||
default [[File:76-EDO_Evo-SZ_Sagittal.svg]] | |||
</imagemap> | |||
In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's [[Sagittal notation#Primary comma|primary comma]] (the comma it ''exactly'' represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it ''approximately'' represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO. | |||
== Instruments == | |||
=== Skip fretting === | |||
'''[[Skip fretting]] system 76 2 17''' optimizes the subminor chord, 0-17-44 of 76edo. | |||
7/6 can be found on adjacent strings, as each string is tuned 17\76 apart. | |||
If you’re playing a 6-string with the lowest string at an arbitrary root within 76edo, the strings will be as follows, from thickest to thinnest: | |||
0 17 34 51 68 9 | |||
Note that the thinnest string is in the next octave. | |||
Each fret is 2\76, or 1\38. This puts the perfect 5th at the 3rd string (34\76), 5th fret (10\76). That gives us 44\76. If you want to add more notes to your chord, 59\76 (12/7) can be found on the 4th string, 4th fret. The 8ve is found on the 5th string, 4th fret. The subminor 10th is found on the 6th string, 4th fret. | |||
A regular minor chord, with a 19\76 3rd, is also easily playable. 19\76 is found on the 2nd string, 1st fret; as well as on the 6th string, 5th fret. | |||
=== Keyboards === | |||
[[Lumatone mapping for 76edo|Lumatone mappings for 76edo]] are available. | |||
== Music == | |||
; [[Bryan Deister]] | |||
* [https://www.youtube.com/shorts/IUqoN9YhTtQ ''microtonal improvisation in 76edo''] (2025) | |||
Latest revision as of 08:29, 2 July 2025
| ← 75edo | 76edo | 77edo → |
76 equal divisions of the octave (abbreviated 76edo or 76ed2), also called 76-tone equal temperament (76tet) or 76 equal temperament (76et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 76 equal parts of about 15.8 ¢ each. Each step represents a frequency ratio of 21/76, or the 76th root of 2.
Theory
76edo's patent val is contorted in the 5-limit, reflecting the fact that 76 = 4 × 19. In the 7-limit it tempers out 2401/2400 in addition to 81/80, and so supports the squares temperament. In the 11-limit, it tempers out 245/242 and 385/384, and supports pombe, the 24 & 26 temperament. In the 13-limit, it tempers out 105/104, 144/143, 351/350 and 364/363. While the 44\76 = 11\19 fifth is already flat, the 43\76 fifth, even flatter, is an almost perfect approximation to the hornbostel temperament's POTE fifth, whereas its sharp fifth, 45\76, makes for an excellent superpyth fifth. Hence you can do hornbostel/mavila, squares/meantone, and superpyth all with the same equal division.
Using the 76dgh val, 76edo provides an excellent tuning for teff temperament, a low-complexity, medium-accuracy, and high-limit (17- or 19-limit) temperament.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -7.22 | -7.37 | -5.67 | +1.35 | +1.31 | -3.69 | +1.20 | +5.57 | +2.49 | +2.90 | +3.30 |
| Relative (%) | -45.7 | -46.7 | -35.9 | +8.6 | +8.3 | -23.3 | +7.6 | +35.3 | +15.8 | +18.4 | +20.9 | |
| Steps (reduced) |
120 (44) |
176 (24) |
213 (61) |
241 (13) |
263 (35) |
281 (53) |
297 (69) |
311 (7) |
323 (19) |
334 (30) |
344 (40) | |
Subsets and supersets
Since 76 factors into 22 × 19, 76edo has subset edos 2, 4, 19, and 38. 152edo, which doubles it, is a zeta peak edo.
Intervals
| Steps | Cents | Approximate ratios | Ups and downs notation (Dual flat fifth 44\76) |
Ups and downs notation (Dual sharp fifth 45\76) |
|---|---|---|---|---|
| 0 | 0 | 1/1 | D | D |
| 1 | 15.8 | ^D, ^E♭♭♭ | ^D, vvE♭ | |
| 2 | 31.6 | ^^D, vvE♭♭ | ^^D, vE♭ | |
| 3 | 47.4 | 36/35, 38/37 | vD♯, vE♭♭ | ^3D, E♭ |
| 4 | 63.2 | 29/28 | D♯, E♭♭ | ^4D, ^E♭ |
| 5 | 78.9 | 23/22 | ^D♯, ^E♭♭ | ^5D, ^^E♭ |
| 6 | 94.7 | ^^D♯, vvE♭ | v5D♯, ^3E♭ | |
| 7 | 110.5 | vD𝄪, vE♭ | v4D♯, ^4E♭ | |
| 8 | 126.3 | 14/13 | D𝄪, E♭ | v3D♯, ^5E♭ |
| 9 | 142.1 | ^D𝄪, ^E♭ | vvD♯, v5E | |
| 10 | 157.9 | 34/31 | ^^D𝄪, vvE | vD♯, v4E |
| 11 | 173.7 | 32/29 | vD♯𝄪, vE | D♯, v3E |
| 12 | 189.5 | 19/17, 29/26, 39/35 | E | ^D♯, vvE |
| 13 | 205.3 | ^E, ^F♭♭ | ^^D♯, vE | |
| 14 | 221.1 | 33/29 | ^^E, vvF♭ | E |
| 15 | 236.8 | vE♯, vF♭ | ^E, vvF | |
| 16 | 252.6 | 22/19, 37/32 | E♯, F♭ | ^^E, vF |
| 17 | 268.4 | 7/6 | ^E♯, ^F♭ | F |
| 18 | 284.2 | 33/28 | ^^E♯, vvF | ^F, vvG♭ |
| 19 | 300 | 19/16, 25/21 | vE𝄪, vF | ^^F, vG♭ |
| 20 | 315.8 | 6/5 | F | ^3F, G♭ |
| 21 | 331.6 | 23/19 | ^F, ^G♭♭♭ | ^4F, ^G♭ |
| 22 | 347.4 | ^^F, vvG♭♭ | ^5F, ^^G♭ | |
| 23 | 363.2 | vF♯, vG♭♭ | v5F♯, ^3G♭ | |
| 24 | 378.9 | F♯, G♭♭ | v4F♯, ^4G♭ | |
| 25 | 394.7 | ^F♯, ^G♭♭ | v3F♯, ^5G♭ | |
| 26 | 410.5 | 33/26 | ^^F♯, vvG♭ | vvF♯, v5G |
| 27 | 426.3 | vF𝄪, vG♭ | vF♯, v4G | |
| 28 | 442.1 | F𝄪, G♭ | F♯, v3G | |
| 29 | 457.9 | ^F𝄪, ^G♭ | ^F♯, vvG | |
| 30 | 473.7 | ^^F𝄪, vvG | ^^F♯, vG | |
| 31 | 489.5 | vF♯𝄪, vG | G | |
| 32 | 505.3 | G | ^G, vvA♭ | |
| 33 | 521.1 | 23/17 | ^G, ^A♭♭♭ | ^^G, vA♭ |
| 34 | 536.8 | ^^G, vvA♭♭ | ^3G, A♭ | |
| 35 | 552.6 | 11/8 | vG♯, vA♭♭ | ^4G, ^A♭ |
| 36 | 568.4 | 25/18, 32/23 | G♯, A♭♭ | ^5G, ^^A♭ |
| 37 | 584.2 | 7/5 | ^G♯, ^A♭♭ | v5G♯, ^3A♭ |
| 38 | 600 | ^^G♯, vvA♭ | v4G♯, ^4A♭ | |
| 39 | 615.8 | 10/7 | vG𝄪, vA♭ | v3G♯, ^5A♭ |
| 40 | 631.6 | 23/16, 36/25 | G𝄪, A♭ | vvG♯, v5A |
| 41 | 647.4 | 16/11 | ^G𝄪, ^A♭ | vG♯, v4A |
| 42 | 663.2 | ^^G𝄪, vvA | G♯, v3A | |
| 43 | 678.9 | 34/23 | vG♯𝄪, vA | ^G♯, vvA |
| 44 | 694.7 | A | ^^G♯, vA | |
| 45 | 710.5 | ^A, ^B♭♭♭ | A | |
| 46 | 726.3 | ^^A, vvB♭♭ | ^A, vvB♭ | |
| 47 | 742.1 | vA♯, vB♭♭ | ^^A, vB♭ | |
| 48 | 757.9 | A♯, B♭♭ | ^3A, B♭ | |
| 49 | 773.7 | ^A♯, ^B♭♭ | ^4A, ^B♭ | |
| 50 | 789.5 | ^^A♯, vvB♭ | ^5A, ^^B♭ | |
| 51 | 805.3 | vA𝄪, vB♭ | v5A♯, ^3B♭ | |
| 52 | 821.1 | 37/23 | A𝄪, B♭ | v4A♯, ^4B♭ |
| 53 | 836.8 | ^A𝄪, ^B♭ | v3A♯, ^5B♭ | |
| 54 | 852.6 | ^^A𝄪, vvB | vvA♯, v5B | |
| 55 | 868.4 | 33/20, 38/23 | vA♯𝄪, vB | vA♯, v4B |
| 56 | 884.2 | 5/3 | B | A♯, v3B |
| 57 | 900 | 32/19, 37/22 | ^B, ^C♭♭ | ^A♯, vvB |
| 58 | 915.8 | ^^B, vvC♭ | ^^A♯, vB | |
| 59 | 931.6 | 12/7 | vB♯, vC♭ | B |
| 60 | 947.4 | 19/11 | B♯, C♭ | ^B, vvC |
| 61 | 963.2 | ^B♯, ^C♭ | ^^B, vC | |
| 62 | 978.9 | ^^B♯, vvC | C | |
| 63 | 994.7 | vB𝄪, vC | ^C, vvD♭ | |
| 64 | 1010.5 | 34/19 | C | ^^C, vD♭ |
| 65 | 1026.3 | 29/16 | ^C, ^D♭♭♭ | ^3C, D♭ |
| 66 | 1042.1 | 31/17 | ^^C, vvD♭♭ | ^4C, ^D♭ |
| 67 | 1057.9 | vC♯, vD♭♭ | ^5C, ^^D♭ | |
| 68 | 1073.7 | 13/7 | C♯, D♭♭ | v5C♯, ^3D♭ |
| 69 | 1089.5 | ^C♯, ^D♭♭ | v4C♯, ^4D♭ | |
| 70 | 1105.3 | ^^C♯, vvD♭ | v3C♯, ^5D♭ | |
| 71 | 1121.1 | vC𝄪, vD♭ | vvC♯, v5D | |
| 72 | 1136.8 | C𝄪, D♭ | vC♯, v4D | |
| 73 | 1152.6 | 35/18, 37/19 | ^C𝄪, ^D♭ | C♯, v3D |
| 74 | 1168.4 | ^^C𝄪, vvD | ^C♯, vvD | |
| 75 | 1184.2 | vC♯𝄪, vD | ^^C♯, vD | |
| 76 | 1200 | 2/1 | D | D |
Notation
Ups and downs notation
76edo can be notated with ups and downs, spoken as up, dup, downsharp, sharp, upsharp etc. and down, dud, upflat etc. Note that dup is equivalent to dudsharp and dud is equivalent to dupflat.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|||||||||
| Flat symbol | |
|
Using Helmholtz–Ellis accidentals, 76edo can also be notated using ups and downs notation along with Stein–Zimmerman quarter-tone accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
| ||
| Flat symbol | |
|
|
|
|
|
Here, a sharp raises by four steps, and a flat lowers by four steps, so arrows can be used to fill in the gap.
Sagittal notation
This notation uses the same sagittal sequence as EDOs 62 and 69, and is a superset of the notations for EDOs 38 and 19.
Evo flavor

Revo flavor

Evo-SZ flavor

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.
Instruments
Skip fretting
Skip fretting system 76 2 17 optimizes the subminor chord, 0-17-44 of 76edo.
7/6 can be found on adjacent strings, as each string is tuned 17\76 apart.
If you’re playing a 6-string with the lowest string at an arbitrary root within 76edo, the strings will be as follows, from thickest to thinnest:
0 17 34 51 68 9
Note that the thinnest string is in the next octave.
Each fret is 2\76, or 1\38. This puts the perfect 5th at the 3rd string (34\76), 5th fret (10\76). That gives us 44\76. If you want to add more notes to your chord, 59\76 (12/7) can be found on the 4th string, 4th fret. The 8ve is found on the 5th string, 4th fret. The subminor 10th is found on the 6th string, 4th fret.
A regular minor chord, with a 19\76 3rd, is also easily playable. 19\76 is found on the 2nd string, 1st fret; as well as on the 6th string, 5th fret.
Keyboards
Lumatone mappings for 76edo are available.