Yer
Introduction
Yer is an octave-reduced EFG (Euler-Fokker genus) of 11, 13, 17, and 19. As such it is a 2.11.13.17.19 limit just intonation tuning (ignoring the 3rd, 5th, and 7th harmonics) which is octave-repeating.
Yer has 16 pitches from the EFG, and 2 additional pitches are optional to include; these pitches are very close to other pitches already in the system (off by comma-sized amounts) and are useful as inflections or points to comma-shift on.
Yer was developed by Douglas Blumeyer as a system to explore the unnoticeable comma 2432/2431, the Blumeyer comma, which appears twice as a step in the scale.
| name | 11 | 13 | 17 | 19 | EFG composition | frequency multiplier (definition) | frequency multiplier (decimal) | pitch (¢) | EHEJIPN (on C) |
|---|---|---|---|---|---|---|---|---|---|
| a | 1 | 1/1 | 1 | 0 | 
| ||||
| (q) | 11⋅11⋅17 | 2057/2048 | 1.00439453125 | 7.5912942 | 
| ||||
| o | 13⋅17⋅19 | 4199/4096 | 1.025146484 | 42.9960874 | 
| ||||
| d | 17 | 17/16 | 1.0625 | 104.9554095 | 
| ||||
| f | 11⋅13 | 143/128 | 1.1171875 | 191.8456041 | 
| ||||
| l | 11⋅13⋅17 | 2431/2048 | 1.187011719 | 296.8010136 | 
| ||||
| e | 19 | 19/16 | 1.1875 | 297.5130161 | 
| ||||
| k | 17⋅19 | 323/256 | 1.26171875 | 402.4684256 | 
| ||||
| m | 11⋅13⋅19 | 2717/2048 | 1.326660156 | 489.3586203 | 
| ||||
| b | 11 | 11/8 | 1.375 | 551.3179424 | 
| ||||
| (r) | (13⋅19)/11 | 247/176 | 1.40340909091 | 586.7227355 | 
| ||||
| p | 11⋅13⋅17⋅19 | 46189/32768 | 1.409576416 | 594.3140298 | 
| ||||
| g | 11⋅17 | 187/128 | 1.4609375 | 656.2733519 | 
| ||||
| c | 13 | 13/8 | 1.625 | 840.5276618 | 
| ||||
| h | 11⋅19 | 209/128 | 1.6328125 | 848.8309585 | 
| ||||
| i | 13⋅17 | 221/128 | 1.7265625 | 945.4830713 | 
| ||||
| n | 11⋅17⋅19 | 3553/2048 | 1.734863281 | 953.786368 | 
| ||||
| j | 13⋅19 | 247/128 | 1.9296875 | 1138.040678 | 
|
The diagrams throughout this wiki entry were designed by Douglas Blumeyer. The same four colors are consistently associated with the four harmonics: green is 11, orange is 13, cyan is 17, and magenta is 19.
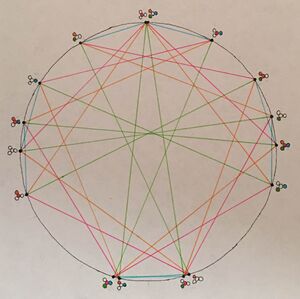
Yer features a minor third of 19:16 and a minor second 17:16.
EFG as combination of CPS's
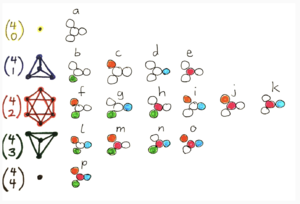
Every pitch in the system is a combination of either zero, one, two, three, or four of 11, 13, 17, or 19, for a total of 1 + 4 + 6 + 4 + 1 = 16 pitches. In other words it is the powerset of {11, 13, 17, 19}. If familiar with Erv Wilson’s Combination Product Sets, or CPS's, it may help to think of an Euler-Fokker Genus as the intersection of the choose-1 tetrany, the choose-2 hexany, and the choose-3 tetrany, plus the unison, plus 11 * 13 * 17 * 19 all together which may be called the aota, an acronym for “all of the above”.
As an EFG, it has no subharmonic factors, that is, no division - only multiplication of them together, which leads to it being ambitonal, not otonal or utonal leaning. While it is nicely “balanced/symmetrical” as all CPSs are, pitches in the resultant system are not evenly distributed. There are two massive gaps of 185 cents, and two places where pitches land almost directly on top of each other.
Blumeyer comma
Those pitches right on top of each other are a feature, not a bug. The pitch 11 * 13 * 17 is 2431, only one off from the pitch 19, which when octave adjusted is 2432. So we end up with this superparticular ratio, 2432:2431, called the Blumeyer comma.
| name | value | cents | prime exponent vector |
|---|---|---|---|
| Blumeyer comma | 2432/2431 | 0.71200249782 | | 7 0 0 0 -1 -1 -1 1 > |
Perhaps, given its tiny size, it would be better called the Blumeyer schismina.
Lattice Play
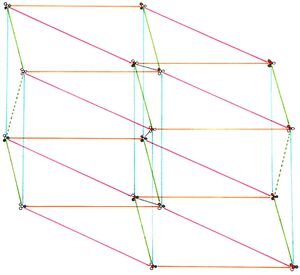
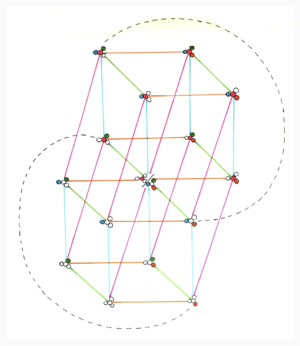
Since the EFG system of Yer includes both 11 * 13 * 17 and 19 as pitches, that means the comma exists as an interval in the scale. Since it’s so tiny, though, the two notes related by it can hardly be treated as separate. This means that when you go to draw this tuning out as a JI lattice, you can do something you wouldn’t normally do, which is set a couple points right together.
You could think of this lattice as a pair of cubes. One is an Euler-Fokker genus of [11, 13, 17]. The other is that same Euler-Fokker genus, just with every node multiplied by 19. That’s why every point in the second cube has the same set of circles colored in as the analogous one in the other cube, just with the magenta 19 filled in as well.
So every point in the first cube is connected to the analogous node in the second cube. Normally the node for 19 would not have any direct connection with the node 11, 13, 17. It only directly connects with one node in the other cube, its analogous one, the unison. But here we see that not only is there another effect going on connecting these two nodes, that effect goes beyond connecting them, it straight up conflates them.
But that's not all; recall that there were two other pairs of pitches that were almost the same, too. One of those pairs has such simple sounding members, it may surprise you: 13 and 11 * 19. In this view, we can see that they are nowhere near each other. So we’ll have to nudge our lattice around a little bit more; that's how we arrive at the final lattice shown in the introduction. There, the three pairs of intervals in the center connected by short solid black lines can be modulated between almost unnoticed.
Yama comma
The reason why 13 and 11 * 19 are so close is that it turns out there is *another* comma existing as a step in this tuning of 11’s, 13’s, 17’s, and 19’s. If we move by an eleventh, then a nineteenth, and then down a thirteenth, we end up right back where we started, off by 8.303 cents. That's the yama comma.
| name | value | cents | prime exponent vector |
|---|---|---|---|
| yama comma | 209/208 | 8.303296728 | | -4 0 0 0 1 -1 0 1 > |
Another consequence of the yama comma is that a couple “extra” lattice connections appear. These are drawn in dotted green on the lattices in the introduction. If we move by an eleventh, a seventeenth, and another eleventh, we end up right back where you started, off by 7.591 cents, or in other words, one yama comma minus one Blumeyer comma. We call this the Blume comma.
| name | value | cents | prime exponent vector |
|---|---|---|---|
| Blume comma | 2057/2048 | 7.59129422992 | | -11 0 0 0 2 0 1 > |
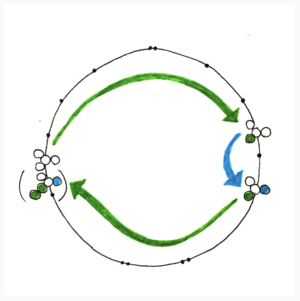
The idea is that if you were to try to go from 11 * 17 by an eleventh to 11 * 11 * 17, well, you’re not really allowed to do that because the EFG does not duplicate factors (you can’t have two 11’s), but since 11 * 11 * 17 is essentially 1, we’ll permit it.
Analogously, you can move from 11 * 13 * 17 * 19 by an eleventh to 11 * 11 * 13 * 17 * 19, or just 13 * 19. Though, for symmetry, we actually do 13 * 19 / 11 rather than 11 * 11 * 13 * 17 * 19.
And as long as we're changing the angle we look on the cube to bring the right pairs of pitches together, we have also taken care to balance these dotted lines with the real 11 lines, so that it’s the zig to the zag of the real 11, more strongly suggesting the dimension of the 11th harmonic’s relationship to that of the 17th (i.e that two 11's make a 17).
Now we could have drawn dotted lines connecting 11 * 13 * 17 to 13, but declined, considering that the ability to move between these two pitches is already achievable by modulating from from 11 * 13 * 17 to 19, then moving by that 11 to 11 * 19, then modulating to 13. The same goes for the connection between 11 * 17 * 19 and 19. This would be pretty obvious on the cycle view, because we’d just be drawing a dotted line right alongside an existing solid one.
Here’s something else interesting: we can move by four 11’s in a row. We can move from 17 * 19 to 11 * 17 * 19, which can be shifted to 13 * 17, then move to 11 * 13 * 17, which can be shifted to 19, then move to 11 * 19, which can be shifted to 13, then move to 11 * 13.
You can also move by 3 11’s in a row on the left and right edges; for the other factors, you can only ever move by two of them in a row (in sad 17’s case, only one spot where you can do that, which happens to be in parallel to the spot where you can 4x by 11).
Comma pumps
Yer is pure JI, but due to the five places where it boasts two pitches very close together but with very different harmonic compositions, it can achieve zero comma pumps by “comma shifting” at those key points, returning to exactly their original pitch.
In Yer, there are three classes of pumps of the Blumeyer comma. One way of defining them is by which harmonic is opposite the 19. So in class a, it’s the 11, in b it’s the 13, and in c it’s the 17.
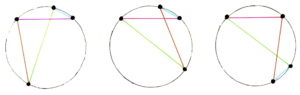
This diagram shows real instances of these pumps in Yer and then rotates each of these three diagrams by a different amount so that the 19 would be horizontal across the top in each one, in order to better bring out their differences in shape.
Each of these families has a mirror image. You can achieve it by either reversing the order you move by those harmonics, or flipping the harmonic directions you move (from harmonic to subharmonic, or vice versa). I call a reversal like this a “counter”, as in “counterclockwise”, (because in this case we are reversing a cycle, so counter is appropriate, and there is another place soon where I need the word “reverse” and I didn’t want to use “retrograde”) and I call a flipping like this an inversion, as in inverting a fraction’s numerator and denominator, which it is.
That is you could counter:
up 19, down 17, down 13, down 11
to
down 11, down 13, down 17, up 19
Or you could invert:
up 19, down 17, down 13, down 11
to
down 19, up 17, up 13, up 11.
The difference between a counter and an invert is only in which direction you flow through the comma; the shape is the same between them, i.e. the mirror image of the original. So if you do *both*, you stay in the same position/shape, but the flow through your shape is in the opposite direction. That’s “reverse”.
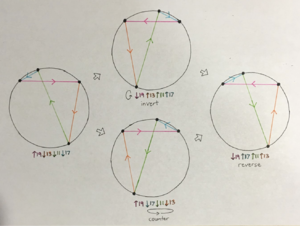
There’s another operation which does not change the shape, and that’s “cycling” which is changing which of the four notes you start on.
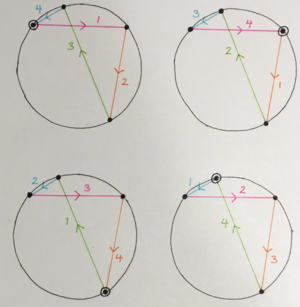
Finally there are several possible rotations of each comma within Yer, a rotation being a changing of the position within the octave circle. There are five each, to be exact: one for where each of its four corners touches the Blumeyer comma interval, plus one which uses the Blume commas.
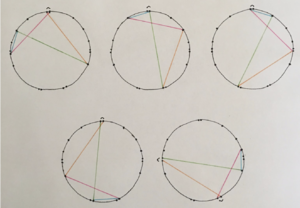
So with three comma pump families, each with four total forms (base, inverse, converse, and reverse), each of those with four possible starting positions or cyclings, and each of those with five possible rotations, Yer boasts 3 * 4 * 4 * 5 = 240 total possible comma pumps.
I haven’t much explored the Blume comma’s pumps, but those would be much simpler. Basically for each 17 interval, make a long skinny triangle across the circle out of its two 11s.
So you could write music with these comma pumps. The first piece I’ve written with Yer, in fact, uses three variations on one comma pump family, interrupting each other to create a sort of “meta-pump”. That’s a horrible term, though, don’t use that. Because they’re not really full pumps anymore, they’re partial ones. I’ll think of something later.
Another Lens
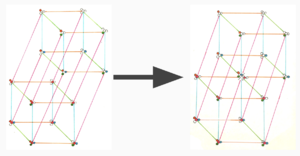
There’s another lens I’d like to look at Yer through. This will take a few steps. As I mentioned before, you can think of our EFG as two EFGs of the next smallest order, with each node in one connected to the analogous node of the other. EFGs build on each other like that. And in fact, of this order 4 EFG, you could pick any other of our four harmonics, not just 19 works this way, split the lattice on it, and you’ll end up with a pair of cubes. Here I’ve shown all of these, just without the bonds of the harmonics dividing them.
Considered as a whole, these are the 8 cubic faces of the tesseract, or hypercube, of our order 4 EFG.
But 19 still is the more interesting one. First, look at the lattice view on the left, to get a sense of the blue cube, the base EFG, and the red cube, which represents the EFG with every node multiplied by 19. Next, look at the cycle view, and see how that coloring transfers there.
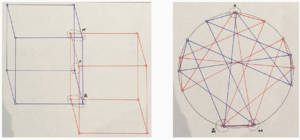
Now suppose we take the red cube and the blue cube, and for each of them instead color code for their constituent harmonic intervals. The blue becomes this on the left, the red becomes that on the right. Now it becomes clear how rotating the blue cube around the cycle by a 19th brings those three pairs of pitches together.
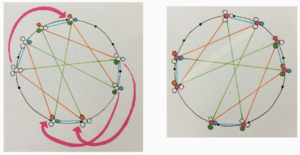
Here’s an extreme subtlety, but worth mentioning I think in case it confuses anyone else as bad as it did me. It’s really easy to look at these two diagrams and think “mirror image” (across the vertical axis), but that’s deceptive. The unison and the aota are *not* connected by a diameter here. They are not on opposite sides of the octave circle. That is because a movement by all intervals is not 600 cents, but only 594. Remember that the 19th harmonic is 298 cents, and the other three harmonics in the system together are almost exactly the same. So if you wanted to orient Yer so that its line of symmetry is perfectly vertical (which I submit makes a good amount of sense) Then you must also stay aware that the unsion and aota are not at the 180 degree and 0 degree positions, but more like 179.5 and 0.5 degree positions.
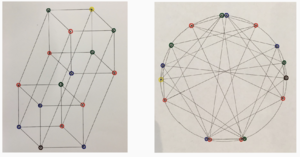
We can also delve a little deeper into Yer in terms of its constituent CPS’s. In the lattice view on the left, you can see how the unison and aota are opposite extreme corners, and their immediately adjacent nodes are all tetrany members — choose 1 wrapping unison, choose 3 wrapping the aota — and all nodes two moves away from them are in the hexany. In other words, no node of a given color touches any other nodes of its own color. Only green touches yellow, only blue touches brown, and red buffers between green and blue. I could have drawn these diagrams with the black lines replaced/augmented with dotted lines or arrows of color indicating the two types they each bridge.
Then here’s what we get when we actually render the CPSs and their connections within themselves. You’ll notice that these lines are completely different from the black ones. The black ones connect pitches separated by single harmonic factors. The nature of CPSs, though, is that pitches are connected when they are separated by two harmonic factors. For example, in the choose-1 tetrany, the members are just the single harmonics 11, 13, 17, 19. So 11 and 17 are related not by a single harmonic factor, but by 11:17 or 17:11; two factors.
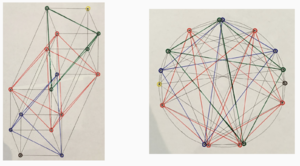
In the tetrany, every node connects to every other node, But in the hexany that is not the case. Remember the hexany is our choose-2 set, for consider for example the pair of nodes 11*13, and 17*19. They do not share a factor, so they are not connected. The pair of nodes 11*13 and 11*19, however, share an 11, so the 11’s cancel out, and again you have a relationship based on two factors, in this case 13:19. This view is terribly busy, though. Too much information. But if you pull away the black lines for single harmonic relationships, which we already talked about a lot with respect to commas and pumps thereof...
...you can actually begin to see stuff. In the lattice view on the left, notice how the tetranies take form as tetrahedrons and the hexany as an octahedron. In the cyclical view on the right, you can see how the choose-1 and choose-3 tetranies, the blue and green shapes, are reflections of each other across a vertical line drawn down this circle, as well as how the choose 2 hexany is symmetrical across the same line, and the remaining two notes - the unison and the aota - are located symmetrically to each other. You could write music with just these CPSs.
Intervals
| 1 | 13⋅17⋅19 | 17 | 11⋅13 | 11⋅13⋅17 | 19 | 17⋅19 | 11⋅13⋅19 | 11 | 11⋅13⋅17⋅19 | 11⋅17 | 13 | 11⋅19 | 13⋅17 | 11⋅17⋅19 | 13⋅19 | |
| 1 | 0 | 42.9960874 | 104.9554095 | 191.8456041 | 296.8010136 | 297.5130161 | 402.4684256 | 489.3586203 | 551.3179424 | 594.3140298 | 543.7266481 | 359.4723382 | 351.1690415 | 254.5169287 | 246.213632 | 61.9593221 |
| 13⋅17⋅19 | 0 | 61.9593221 | 148.8495167 | 253.8049262 | 254.5169287 | 359.4723382 | 446.3625329 | 508.321855 | 551.3179424 | 586.7227355 | 402.4684256 | 394.1651289 | 297.5130161 | 289.2097194 | 104.9554095 | |
| 17 | 0 | 86.89019463 | 191.8456041 | 192.5576066 | 297.5130161 | 384.4032108 | 446.3625329 | 489.3586203 | 551.3179424 | 464.4277477 | 456.124451 | 359.4723382 | 351.1690415 | 166.9147316 | ||
| 11⋅13 | 0 | 104.9554095 | 105.667412 | 210.6228215 | 297.5130161 | 359.4723382 | 402.4684256 | 464.4277477 | 551.3179424 | 543.0146456 | 446.3625329 | 438.0592361 | 253.8049262 | |||
| 11⋅13⋅17 | 0 | 0.7120024978 | 105.667412 | 192.5576066 | 254.5169287 | 297.5130161 | 359.4723382 | 543.7266481 | 552.0299449 | 551.3179424 | 543.0146456 | 358.7603357 | ||||
| 19 | 0 | 104.9554095 | 191.8456041 | 253.8049262 | 296.8010136 | 358.7603357 | 543.0146456 | 551.3179424 | 552.0299449 | 543.7266481 | 359.4723382 | |||||
| 17⋅19 | 0 | 86.89019463 | 148.8495167 | 191.8456041 | 253.8049262 | 438.0592361 | 446.3625329 | 543.0146456 | 551.3179424 | 464.4277477 | ||||||
| 11⋅13⋅19 | 0 | 61.9593221 | 104.9554095 | 166.9147316 | 351.1690415 | 359.4723382 | 456.124451 | 464.4277477 | 551.3179424 | |||||||
| 11 | 0 | 42.9960874 | 104.9554095 | 289.2097194 | 297.5130161 | 394.1651289 | 402.4684256 | 586.7227355 | ||||||||
| 11⋅13⋅17⋅19 | 0 | 61.9593221 | 246.213632 | 254.5169287 | 351.1690415 | 359.4723382 | 543.7266481 | |||||||||
| 11⋅17 | 0 | 184.2543099 | 192.5576066 | 289.2097194 | 297.5130161 | 481.767326 | ||||||||||
| 13 | 0 | 8.303296728 | 104.9554095 | 113.2587062 | 297.5130161 | |||||||||||
| 11⋅19 | 0 | 96.65211277 | 104.9554095 | 289.2097194 | ||||||||||||
| 13⋅17 | 0 | 8.303296728 | 192.5576066 | |||||||||||||
| 11⋅17⋅19 | 0 | 184.2543099 | ||||||||||||||
| 13⋅19 | 0 |
| ratio | type | count | prime exponent vector | cents | gap between available interval classes | lower limit interval to nearest in Yer | cents difference up | cents different down (to prove how they're right in between | inverse ratio | inverse cents |
|---|---|---|---|---|---|---|---|---|---|---|
| 2431:2432 | 3v1 | 1 | | 7 0 0 0 -1 -1 -1 1 > | 0.7120024978 | 0.7120024978 | 1199.287998 | ||||
| 208:209 | 2v1 | 2 | 13 -> 11 19 | 8.303296728 | 7.59129423 | 1191.696703 | ||||
| 4096:4199 | 3v0 | 2 | 1 -> 13 17 19 | 42.9960874 | 34.69279067 | 48:49 | 35.69681207 - | 35.69681207 - | 1157.003913 | |
| 247:256 | 2v0 | 4 | 13 19 | 61.9593221 | 18.9632347 | 24:25 | 70.67242686 - | 70.67242686 - | 1138.040678 | |
| 136:143 | 2v1 | 2 | 17 : 11 13 | 86.89019463 | 24.93087253 | 20:21 | 84.46719347 - | 84.46719347 - | 1113.109805 | |
| 209:221 | 2v2 | 1 | 11 19 : 13 17 | 96.65211277 | 9.76191814 | 1103.347887 | ||||
| 16:17 | 1v0 | 8 | 16:17 | 104.9554095 | 8.30329673 | 1095.044591 | ||||
| 143:152 | 2v1 | 2 | 11 13 : 19 | 105.667412 | 0.7120025 | 1094.332588 | ||||
| 3328:3553 | 3v1 | 1 | 13 : 11 17 19 | 113.2587062 | 7.5912942 | 15:16, 15:14 | 111.7312853 -, 119.4428083 - | 111.7312853 -, 119.4428083 - | 1086.741294 | |
| 323:352 | 2v1 | 2 | 11 : 17 19 | 148.8495167 | 35.5908105 | 32:35 | 155.1396203 - | 155.1396203 - | 1051.150483 | |
| 247:272 | 2v1 | 2 | 17 : 13 19 | 166.9147316 | 18.0652149 | 1033.085268 | ||||
| 187:208 | 2v1 | 2 | 13 : 11 17 | 184.2543099 | 17.3395783 | 9:10 | 182.4037121 - | 182.4037121 - | 1015.74569 | |
| 128:143 | 2v0 | 4 | 1 : 11 13 | 191.8456041 | 7.5912942 | 1008.154396 | ||||
| 17:19 | 1v1 | 4 | 17:19 | 192.5576066 | 0.7120025 | 25:28 | 196.1984787 - | 196.1984787 - | 1007.442393 | |
| 286:323 | 2v2 | 1 | 11 13 : 17 19 | 210.6228215 | 18.0652149 | 8:9 | 203.9100017 - | 203.9100017 - | 989.3771785 | |
| 3553:4096 | 3v0 | 2 | 1 : 11 17 19 | 246.213632 | 35.5908105 | 7:8 | 231.174094 - | 231.174094 - | 953.786368 | |
| 19:22 | 1v1 | 4 | 19 : 11 | 253.8049262 | 7.5912942 | 946.1950738 | ||||
| 221:256 | 2v0 | 4 | 13 17 | 254.5169287 | 0.7120025 | 7:6 | 266.870906 - | 266.870906 - | 945.4830713 | |
| 11:13 | 1v1 | 4 | 11:13 | 289.2097194 | 34.6927907 | 910.7902806 | ||||
| 2048:2431 | 3v0 | 2 | 11 13 17 | 296.8010136 | 7.5912942 | 903.1989864 | ||||
| 16:19 | 1v0 | 8 | 297.5130161 | 0.7120025 | 5:6 | 315.641287 - | 315.641287 - | 902.4869839 | ||
| 209:256 | 2v0 | 4 | 11 19 | 351.1690415 | 53.6560254 | 40:49 | 351.3380991 - | 351.3380991 - | 848.8309585 | |
| 152:187 | 2v1 | 2 | 11 17 : 19 | 358.7603357 | 7.5912942 | 841.2396643 | ||||
| 13:16 | 1v0 | 8 | 13:16 | 359.4723382 | 0.7120025 | 840.5276618 | ||||
| 2176:2717 | 3v1 | 1 | (11*13*19)/(17*2^7) | 384.4032108 | 24.9308726 | 4:5 | 386.313714 - | 386.313714 - | 815.5967892 | |
| 176:221 | 2v1 | 2 | 11 : 13 17 | 394.1651289 | 9.7619181 | 805.8348711 | ||||
| 256:323 | 2v0 | 4 | 17 19 | 402.4684256 | 8.3032967 | 797.5315744 | ||||
| 323:416 | 3v0 | 2 | 17 19 13 | 438.0592361 | 35.5908105 | 7:9, 25:32 | 435.0840953 -, 427.3725723 - | 435.0840953 -, 427.3725723 - | 761.9407639 | |
| 17:22 | 1v1 | 4 | 17 11 | 446.3625329 | 8.3032968 | 753.6374671 | ||||
| 209:272 | 2v1 | 2 | 17 : 11 19 | 456.124451 | 9.7619181 | 743.875549 | ||||
| 13:17 | 1v1 | 4 | 464.4277477 | 8.3032967 | 16:21, 49:64 | 470.7809073 -, 462.3481871- | 470.7809073 -, 462.3481871- | 735.5722523 | ||
| 187:247 | 2v2 | 1 | 11 17 : 13 19 | 481.767326 | 17.3395783 | 718.232674 | ||||
| 2048:2717 | 2v1 | 2 | 11 13 19 | 489.3586203 | 7.5912943 | 3:4 | 498.044999 - | 498.044999 - | 710.6413797 | |
| 4199:5632 | 3v1 | 1 | (11*2^9)/(13*17*19) | 508.321855 | 18.9632347 | 691.678145 | ||||
| 19:26 | 1v1 | 4 | 19:26 | 543.0146456 | 34.6927906 | 656.9853544 | ||||
| 187:256 | 2v0 | 4 | 11 17 | 543.7266481 | 0.7120025 | 35:48 | 546.8153805 - | 546.8153805 - | 656.2733519 | |
| 8:11 | 1v0 | 8 | 8:11 | 551.3179424 | 7.5912943 | 648.6820576 | ||||
| 221:304 | 2v1 | 2 | 13 17 : 19 | 552.0299449 | 0.7120025 | 647.9700551 | ||||
| 176:247 | 2v1 | 2 | 13 19 | 586.7227355 | 34.6927906 | 5:7 | 582.512193 - | 582.512193 - | 613.2772645 | |
| 32768:46189 | 4v0 | 1 | | 15 0 0 0 1 1 1 1 > | 594.3140298 | 7.5912943 | 605.6859702 |
Scala file
! yer.scl ! Yer, EFG of 11, 13, 17, 19 16 ! 4199/4096 17/16 143/128 2431/2048 19/16 323/256 2717/2048 11/8 46189/32768 187/128 13/8 209/128 221/128 3553/2048 247/128 2/1
Video explanation
More details are presented in this video: Yer (pitch system)
Listening
Douglas Blumeyer - Tsraxcfaubdj
Douglas Blumeyer - Blumeyer Comma JI Unpump
Chris Vaisvil - Now Yer Talkin'
Tritave-Based Yer
One could imagine a tritave-repeating variation of Yer, where 2's are out but 3's are in (the EFG of 11, 13, 17, 19 remains but is tritave-reduced instead).
Yer as a temperament
If you temper out only the Blumeyer comma, you get this 2.11.13.17.19 subgroup mapping, which naturally should be called "Blumeyer temperament":
[ ⟨ 1 0 0 0 -7 ] ⟨ 0 1 0 0 1 ] ⟨ 0 0 1 0 1 ] ⟨ 0 0 0 1 1 ] ⟩
Expressed as a map-merge of ETs, that's 13&113&137&194. So one ~19 is up one each of the ~11, ~13, and ~17 here.
Now if you temper out the Blumeyer comma and the yama comma (and therefore also the blume comma; in fact, the canonical form of the comma basis appears to be blume and yama, with the Blumeyer comma being a linear combination of them), then you get a rank-3 temperament, with mapping:
[ ⟨ 1 0 0 11 4 ] ⟨ 0 1 0 -2 -1 ] ⟨ 0 0 1 0 1 ] ⟩
Again that's still in the 2.11.13.17.19 subgroup. And this one is the map-merge of 13&24&33, with generators 1200.4457, 4149.8305, 4442.6991 (that 1st generator modulo the period is 548.4934 and the 2nd generator is 841.362). So one ~17 is down two ~11, and one ~19 is down one ~11 and up a ~13. Cool! This you'd call "Yer temperament" then. It has been registered here: No-threes subgroup temperaments#Yer (rank 3)
A 13-note scale with only three scale step sizes is possible here. It's 7L 4M 2s, with the pattern LMLLMLsLMLMLs, where L ≈ 103.4¢, M ≈ 85.9¢, and s ≈ 66.2¢:
! yerMV3.scl ! yer temperament 13-note scale 13 ! 103.4 189.3 292.7 396.1 482.0 585.4 651.7 755.1 841.0 944.4 1030.3 1133.7 (2/1)
However this is not quite an MV3 scale. It is a rotation of the "LLMLsLMLMLsLM" pattern which is identified here as "Conditional (MM=Ls)", and while it's quite close, L + s = 103.4 + 66.2 = 169.6 but 169.6/2 = 84.8, not 85.9 which is the M here.
The lattice for this scale looks like:
| - | (-2,2)
11·13·17·19 13·19/11 585.4¢ |
(-1,2)
13·19
1133.7¢ |
(0,2)
11·13·19
482.0¢ |
(1,2)
11·13²
1030.3¢ |
| (-3,1)
17·19
396.1¢ |
(-2,1)
13·17 11·17·19 944.4¢ |
(-1,1)
11·13·17 19 292.7¢ |
(0,1)
13 11·19 841.0¢ |
(1,1)
11·13
189.3¢ |
| (-3,0)
17·19/13 17/11 755.1¢ |
(-2,0)
17
103.4¢ |
(-1,0)
11·17
651.7¢ |
(0,0)
1 11²·17 0¢ |
- |
See also
Musical Patterns - select Tsraxcfaubdj (GitHub page is here to explore the programmatic reasoning behind how this piece uses Yer: https://github.com/MusicalPatterns/pattern-tsraxcfaubdj)
Hilim13, another tridecatonic tuning in the 2.11.13.17.19 subgroup, JI, designed by Gene Ward Smith
Gjaeck, another tuning in the 2.11.13.17.19 subgroup, a tempered MOS of 57ed2, also designed by Douglas Blumeyer