Gjaeck
Gjaeck is a tridecatonic (5L 8s) MOS scale of 57-EDO optimized for the prime harmonics 11, 13, 17, and 19, while not optimizing for the simpler prime harmonics 3, 5, and 7.
Temperings
The simple map for 57-ET (57p) in the 2.11.13.17.19 domain is ⟨57 197 211 233 242], resulting in the following mappings:
| prime | mapped (decimal) | mapped (definition) | scale steps | octave reduced scale steps | octave reduced interval | pitch (¢) | error (¢) |
|---|---|---|---|---|---|---|---|
| 11 | 10.9749339402 | 2^(197/57) | 197 | 197 mod 57 = 26 | 11/8 | 547.368 | 547.368 - 551.318 = -3.950 |
| 13 | 13.011851757 | 2^(211/57) | 211 | 211 mod 57 = 40 | 13/8 | 842.105 | 842.105 - 840.527 = 1.578 |
| 17 | 17.0030222301 | 2^(233/57) | 233 | 233 mod 57 = 5 | 17/16 | 105.263 | 105.263 - 104.955 = 0.308 |
| 19 | 18.9695563769 | 2^(242/57) | 242 | 242 mod 57 = 14 | 19/16 | 294.737 | 294.737 - 297.513 = -2.776 |
The Blumeyer comma is tempered out by 57p.
| name | value | cents | prime exponent vector |
|---|---|---|---|
| Blumeyer comma | 2432/2431 | 0.71200249782 | [7 0 0 0 -1 -1 -1 1⟩ |
We can see that both through multiplying the mapped values:
[math]\displaystyle{ \qquad 10.9749339402 ⋅ 13.011851757 ⋅ 17.0030222301 / 18.9695563769 ≈ 2^7 }[/math]
Or through summing the scale steps:
[math]\displaystyle{ \begin {align} \qquad &197 &+ &211 &+ &233 &- &242 &= &399 = 57 ⋅ 7 \\ \qquad &26 &+ &40 &+ &5 &- &14 &= &57 \end {align} }[/math]
57p tempers out some other high-limit commas too:
- The Blume comma, 2057/2048; moving up by two 11’s and then an 17 gets you nowhere: 26 + 26 + 5 = 57.
- The yama comma, 209/208, since 26 + 14 = 40; moving by an 11 and 19 is the same as moving by a 13
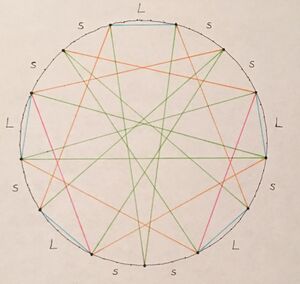
The MOS scale
Gjaeck has a small step equal to 4 steps of 57-EDO and a large step equal to 5 steps. It follows the small and large step sequence:
ssLssLsLssLsL
In this scale we find varying counts of the tempered higher prime harmonics:
- 17/16 exists five times once for each L.
- 19/16 exists twice, once for each LsL.
- 11/8 exists ten times! For each L, you can take the six numbers to the left or the six numbers to the right (looping back around if you reach an edge; this is a cyclical set), and you’ll get it, so this is an 11th-harmonic-heavy mode.
- 13/8 exists six times! Like the 11/8, you can easily find each instance by looking to the L’s: for each one, you can take the nine numbers to the left or the nine numbers to the right and you’ll get it. We only get six 13/8’s because unlike with the 11/8’s, some of them overlap (they connect two L’s together).
While the 11th harmonic is the most prevalent sound, the 19th is the rarest. But since the 19th is the key to the Blumeyer comma, being the one of the four higher harmonics that sits by its lonesome on one side of the ratio while the other three party together, we should pay special attention to the moments in the scale with LsL.
The generator for this MOS is 35th step of 57-EDO, which is 736.8421¢, an interval associated with the 21st harmonic.
While 57 = 19⋅3 and thus 57-EDO extends 19-EDO, Gjaeck bears little resemblance to 19-EDO; it feels more like a whacked out 13-EDO, pinched and pulled in a particular way to more perfectly capture the four higher harmonic primes.
Scala file
! blumeyer_tempered.scl ! Blumeyer comma scale, 5L8s MOS of 57-EDO 13 ! 84.21053 168.42105 273.68421 357.89474 442.10526 547.36842 631.57895 736.84211 821.05263 905.26316 1010.52632 1094.73684 2/1
See also
Hilim13, another tridecatonic tuning in the 2.11.13.17.19 domain, JI, designed by Gene Ward Smith
Yer, another tuning in the 2.11.13.17.19 domain, JI, also designed by Douglas Blumeyer