Maximum variety

The maximum variety (MV) of a scale is a way of quantifying how many different "flavors" of intervals there are in it. Scales with high maximum variety have many different intervals of similar size occuring at different places in the scale. Scales with low maximum variety may be easier for composers and listeners to understand, because there is more uniformity and consistence between different parts of the scale. In a low max-variety scale, simply knowing how many scale steps an interval spans gives you a lot of information about the interval (by narrowing it down to a small set of choices).

An interval class is the set of all interval sizes of a scale which span a given number of steps. For example, in the diatonic scale, the 2-step class consists of the minor third and the major third, because those are the only intervals that are divided into 2 steps of the scale. The "variety" of an interval class is the number of different intervals in it. The maximum variety of a scale is simply the maximum variety of any interval class.

Any scale with all equal steps (such as an EDO) has maximum variety 1. All MOS scales have maximum variety 2. An example of a scale with high max variety is the harmonic series, because the steps get gradually smaller as you go up the scale, and none of them are equal.

Max-variety-3 scales

The commonly discussed MOS property can be characterized as follows, as well as in other equivalent ways: Every set of (non-unison reduced) generic intervals has size at most 2. We can rephrase this as saying that the maximum variety of the scale is 2, or that the scale is maximum variety 2 (MV2). Maximum variety 3 (MV3) is the generalization of the MV2 characterization of the MOS property to ternary scales. Other characterizations of the MOS property, such as distributional evenness and having a generator, do not generalize to properties that are equivalent to MV3 in higher arities.

When discussing scale patterns with three abstract step sizes a, b and c, unlike in the "rank-2" case one must distinguish between unconditionally MV3 scale patterns or abstractly MV3 ones, patterns that are MV3 regardless of what concrete sizes a, b, and c have, and conditionally MV3 patterns, which have tunings that are not MV3. For example, MMLs is conditionally MV3 because it is only MV3 when L, M and s are chosen such that MM = Ls. When we say that an abstract scale pattern is MV3, the former meaning is usually intended.

Classification of MV3 scales

1. A single-period MV3 is either (1) equivalent to XYZYX, (2) equivalent to XYXZXYX, (3) generator-offset with odd length, (4) constructed from 2aX 2bY with a odd and gcd(a, b) = 1 by replacing every other X with Y, or (5) a "twisted" word constructed as follows:
   1. Start with a power of a multimos word w(X, Z) = kaX kbZ such that a is even and each aX bZ subword of w is of the form XP(X, Z)Z where P(X, Z) is a palindrome.
   2. Interchange some of the Z's and X's at some of the borders of these copies of the mos word w.
   3. Replace every other X with Y in w.
2. Single-period MV3 scales not of type (4) are always SV3, and those of type (4) are SV3 with the exception of the n/2-step (n = scale length) which is variety 2.
3. Single-period MV3 scales not of type (1) or (5) are balanced: for any k, any pair of k-steps has a difference that contains +1, -1, or 0 of each step size.

Generating MV3 scales

Once you have chosen a rank-3 temperament and a specific generator interval, there is a mechanical procedure to generate all max-variety-3 scales of a certain size (of which there are, however, infinitely many).

To illustrate this process, let us use the simplest and most familiar rank-3 system: 5-limit JI, and let us use 3/2 as a generator. Because 3/2 is the generator, these max-variety-3 scales will be related (albeit not in a simple 1-to-1 way) with MOSes of Pythagorean, the rank-2 temperament with 3/2 as a generator.

Numbers of notes in Pythagorean MOSes follow the pattern 1+1=2, 2+1=3, 2+3=5, 5+2=7, 5+7=12... (related to the continued fraction for log2(3/2)). The numbers of notes in the 5-limit max-variety-3 scales we're constructing will be related to these by having one of the numbers repeated. Therefore the possible sizes are:

1+1+1=3, 2+1+1=4, 2+2+1=5, 2+2+3=7, 2+3+3=8, 5+2+2=9, 5+5+2=12, 5+5+7=17, 5+7+7=19...

If the number of notes is even, the max-variety-3 scale consists of two chains of 3/2 of equal length, each of which contains half the notes. If the number of notes is odd, the two 3/2-chains differ by 1 in length.

Any scale at all with only 3 notes has max variety 3, so let's begin with the 4-note scales. A 4-note scale consists of two parallel 3/2 intervals separated by some other 5-limit interval. Although strictly speaking this could be any other 5-limit interval at all, if the two chains are separated from each other there will be no potential for 5-limit harmony. For these 4-note scales it turns out that all the configurations work, so we can easily list all the possible scales: ...{1/1,10/9,3/2,5/3}, {1/1,5/4,3/2,5/3}, {1/1,5/4,3/2,15/8}, {1/1,45/32,3/2,125/64}... Only the ones where the two chains are lined up closely have good potential for harmony.

The 5-note scales will consist of a chain of 3 notes and a parallel chain of 2 notes. The 3-note chain has the same pattern as {1/1, 9/8, 3/2}, and in order for it to make an actual max-variety-3 scale, the other 2 notes must fall in between 9/8 and 3/2, and in between 3/2 and 2/1. If either of the notes falls between 1/1 and 9/8, the scale will not be max-variety-3. Let's look at all the scales we get as we move the 2-note chain past the 3-note chain in the 5-limit lattice.

1/1 9/8 40/27 3/2 160/81 ... max variety 3

1/1 10/9 9/8 40/27 3/2 ... fails, max variety 4

1/1 10/9 9/8 3/2 5/3 ... fails, max variety 4

1/1 9/8 5/4 3/2 5/3 ... max variety 3

1/1 9/8 5/4 3/2 15/8 ... max variety 3

1/1 9/8 45/32 3/2 15/8 ... max variety 3

1/1 135/128 9/8 45/32 3/2 ... fails, max variety 4

1/1 135/128 9/8 3/2 405/256 ... fails, max variety 4

1/1 9/8 1215/1024 3/2 405/256 ... max variety 3

Examples testing for MV

MV2

Positive

MV2: For each generic interval class, we find a maximum of 2 different sizes.

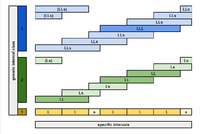
Consider the 5L 2s diatonic scale: LLsLLLs. For each generic interval class, we must confirm that there are only 2 specific intervals:

1. L, s
2. LL, Ls
3. LLL, LLs

Actually we only have to check up to halfway, because all of the generic interval classes beyond this are period complements of the ones we already checked. And so it's confirmed: this is an MV2.

Negative

Not MV2: For the 3rd generic interval class, we find 3 different sizes.

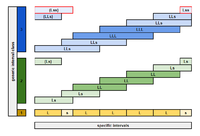
How about a counterexample, LsLLLLs:

1. L, s
2. LL, Ls
3. LLL, LLs, sLs — stop!

We've found that for the generic interval class 3, this scale has three different specific intervals, so it is not MV2.

MV3

Positive

MV3: For each generic interval class, we find a maximum of 3 sizes.

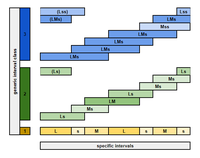
Consider the 2L 2M 3s scale with pattern LsMLsMs.

1. L, M, s
2. Ls, Ms, LM
3. LMs, Mss, Lss

Great, this is MV3.

Negative

Not MV3: For the 2nd generic interval class, we find 4 different sizes.

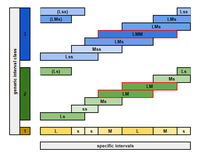
Consider the 2L 2M 3s scale with pattern LssMLMs.

1. L, M, s
2. Ls, ss, Ms, LM — stop!

This scale has more than three different specific intervals for a generic interval class, so it is not MV3.

Conditional

Conditionally MV3: For the 2nd and 3rd generic interval classes, if the condition that MM=Ls is met, then this scale has a maximum of 3 different sizes; otherwise it has 4 and is therefore not MV3.

How about the 2L 3M 2s scale with pattern LMMsMLs.

1. L, M, s
2. LM, MM, Ms, Ls — stop! ...but wait. What if MM=Ls? Then actually this would still be only 3 specific intervals. So let's go with that, and continue.
3. LMM=LLs, MMs, LMs

So this scale is Conditionally MV3 (MM=Ls).