User:FloraC/Analysis on the 13-limit just intonation space: episode ii
This page is a work in progress.
Preface
The Previous Episode mainly discusses how to make sense of the 13-limit JI space. On that basis, this one goes much in depth with the practical side such as interval semiotics, chord construction, chord progression, and some tempering possibilities.
More fundamental context can be found in Fundamental Principles to Musical Sense and There Is Not a Third Side of the River.
Chapter I. Ionian versus Mode 8
Scales generated by octaves and fifths i.e. the 2nd and 3rd harmonics, has proved to be quintessential in functional harmony. It is easy to see how functional harmony unfolds through fifth disposition, up to octave equivalence. The diatonic scale is such an instance. It has been explained how the major tonality demonstrates the presence of harmonics. Now we investigate if there is a specific diatonic mode implied by the major tonality.
In 5-limit JI, the Ionian mode is the clear favorite. The logic is that the diatonic scale can be generated by the three functional positions of the classical major triad. In 13-limit JI, things must be re-evaluated. The chord cannot stay classical. More is different. Let us consider the first 16 harmonics. Mode 8 is a good candidate subject to our account since it is a very coherent scale and chord structure in itself. Assume the root is C, we see each step in mode 8 is mapped to C, D, E, F+, G, Ad, Bb, and B by the interval category scheme introduced in the Previous Episode.

If neutral intervals are taken as exactly half of what it splits, the diatonic generator steps of each step in mode 8 are 0, +2, +4, +5/2, +1, -1/2, -2, and +5, with an average of +3/2. The number has the meaning such that it can be compared to the average brightness of the diatonic modes shown in the following table.
| Mode | UDP | Average Brightness |
|---|---|---|
| Lydian | 0 | +3 |
| Ionian | 1 | +2 |
| Mixolydian | 2 | +1 |
| Dorian | 3 | 0 |
| Aeolian | 4 | -1 |
| Phrygian | 5 | -2 |
| Locrian | 6 | -3 |
Hence, the brightness of mode 8 is halfway between Ionian and Mixolydian. The two diatonic modes' only difference is the quality of the seventh. Indeed, both the minor seventh (precisely the subminor seventh) and the major seventh are present in mode 8, so it all narrows down to which seventh should be the default. This is a question where, when suddenly asked about, one tends to refer to jazz chord notation for an answer – jazz has chosen the minor seventh. Actually, tonality is not a fixed chord structure built on tonic. In common practice, tonality is established through progressions of various functions, dominant–tonic being the most important, and regarding the dominant seventh chord, although itself contains a minor seventh, its third is a major seventh on the tonic. It is this third that is the spirit of the major tonality. For that reason, Ionian remains the most favorable general framework for mode 8, and by extension, for the major tonality in 13-limit JI.
Chapter II. Generic Rooted Chord Construction
It has been demonstrated in the Previous Episode that septimal harmony is characterized by semiquartal harmony, a seemingly different chord construction scheme from the traditional tertian harmony. A question then arises as what essence is abstracted by the chord construction scheme, and what role is played by tertian harmony in the context of 13-limit JI. To answer this, we will investigate how tertian harmony finds harmonics in the process of chord construction, and how each chord contrasts with its negative version.
Any two consecutive odd harmonics in the first 16 give rise to the following intervals.
| Interval | Notation | Interval Class |
|---|---|---|
| 3/1 | C–G | Perfect twelfth |
| 5/3 | G–E | Major sixth |
| 7/5 | E–Bb | Subdiminished fifth |
| 9/7 | Bb–D | Supermajor third |
| 11/9 | D–F+ | Neutral third |
| 13/11 | F+–Ad | Subminor third |
| 15/13 | Ad–B | Superultramajor second |
It seems that all kinds of intervals emerge out of the odd harmonics, but when it comes to compact voices, we find patterns. One prominent frame would involve the split of mode 8 into two octaves. The first octave consists of mode 4; the second octave consists of the other four tones in mode 8.

| Interval | Notation | Interval Class |
|---|---|---|
| 5/4 | C–E | Major third |
| 6/5 | E–G | Minor third |
| 7/6 | G–Bb | Subminor third |
| 9/7 | Bb–D | Supermajor third |
| 11/9 | D–F+ | Neutral third |
| 13/11 | F+–Ad | Subminor third |
| 15/13 | Ad–B | Superultramajor second |
Observably, all except for the last interval are sorted into thirds. It should be noted that this third is to be understood in a loose sense. 9/7 is a third, a supermajor one. 11/9, a neutral one. 13/11, a subminor one. That definitely unveils tertian harmony's central role in 13-limit JI, but moreover, semiquartal harmony is inevitable as well in light of their close association.
To get an impression about this association, the pitch spectrum can be viewed as composed of segments such that each octave has two segments, with the lower segment ranging from 1 to 3/2, and the upper segment ranging from 3/2 to 2/1. The lower segment spans a fifth, so it calls for tertian construction, for which the classical triads are examples as 5/4 is in this segment. The upper segment spans a fourth, so it calls for semiquartal construction, for which the septimal triads are examples as 7/4 is in this segment.
Applying all that has been discussed, the just major chord, built on C, can be extended as
- CM (C–E–G)
- C7 (C–E–G–Bb)
- C9 (C–E–G–Bb–D)
- C11 (C–E–G–Bb–D–F+)
- C13 (C–E–G–Bb–D–F+–Ad)
- C15 (C–E–G–Bb–D–F+–Ad–B)
It is basically the traditional jazz chord notation, with some deviation. The "eleventh" is by default semiaugmented and literally represents the 11th harmonic; the "thirteenth" is by default neutral and literally represents the 13th harmonic. The "fifteenth" is similar. The symbols are mostly logical except that C5 has been taken to indicate a bare fifth, and that CM is used in place of where C5 is supposed to be.
In summary, the just major chord is a four-segment eight-tone chord spanning two octaves, as
[math]\displaystyle{ \displaystyle 1–5/4–3/2–7/4–9/4–11/4–13/4–15/4 }[/math]
According to the principles of harmony dualism, it has a negative version with the same number of segments and the same number of tones in each segment (besides the root and the fifth, which are on the boundaries), so that every tone has something to contrast to in the inverse. The development of the negative version can be concisely described by the intrasegmental inversion rule:
- Intrasegmental inversion rule
- The operation of inversion should flip each segment in place.
The negative version, the just minor chord, is therefore
[math]\displaystyle{ \displaystyle 1–6/5–3/2–12/7–24/11–8/3–16/5–48/13 }[/math]
Indeed, the structure is similar. The thirds contrast by 25/24. The sevenths contrast by 49/48. The ninths and the elevenths contrast by 33/32. The thirteenth and the fifteenth contrast by 65/64. Furthermore, both versions are dyadically concordant since all the dyads are in the 21-odd-limit tonality diamond. Besides the root and the fifth, taking any intervals from the two chords typically makes sense. The figure below illustrates all the segments and the inversion.
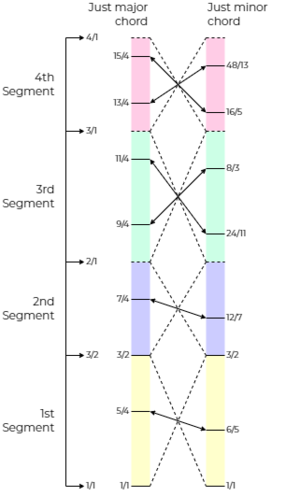
More readily, we can take individual segments as chords. These chords are neat in that each segment can be taken to represent one of the primes in 5, 7, 11, and 13. For example, the first segment is the just major/minor triad; the second segment is the just major/minor semiquartal triad, with the semiquartal voicing rule:
- Semiquartal voicing rule
- The fifth should be transposed to the second octave if only the upper segment is used.
We take the third segment to make really basic use of undecimal intervals. It has a very pleasant sound. Called the just micromajor tetrad and the just microminor tetrad, the two versions are
[math]\displaystyle{ \displaystyle 1–9/8–11/8–3/2 \\ 1–12/11–4/3–3/2 }[/math]
We take the fourth segment to make really basic use of tridecimal intervals, though it involves a classical interval as well. Called the just micromajor semiquartal tetrad and the just microminor semiquartal tetrad, the two versions are
[math]\displaystyle{ \displaystyle 1–13/8–15/8–3 \\ 1–8/5–24/13–3 }[/math]
The names will be explained in the next chapter.
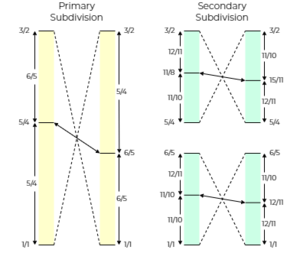
Since 5/4 and 11/8 are in the lower segment, and 7/4 and 13/8 are in the upper segment, we notice they tend to work together. Superposing the first and the third segment produces a supercompact segment. Called the just major pentad and the just minor pentad, the two versions are
[math]\displaystyle{ \displaystyle 1–9/8–5/4–11/8–3/2 \\ 1–12/11–6/5–4/3–3/2 }[/math]
9/8 or 11/8 can be omitted to maximize the concordance; the same can be said for 12/11 or 4/3 in the negative version. But they should be present if complete contrast between the two chords is desired.
Similarly, the second and the fourth segment can be superposed. Called the just major semiquartal pentad and the just minor semiquartal pentad, the two versions are
[math]\displaystyle{ \displaystyle 1–13/8–7/4–15/8–3 \\ 1–8/5–12/7–24/13–3 }[/math]
13/8 or 15/8 in the positive version and 8/5 or 24/13 in the negative version can be omitted for the same reason as above.
Concatenating the two supercompact segments produces the supercompact voicing of the chord, whose positive version is identical to mode 8. The two versions are
[math]\displaystyle{ \displaystyle 1–9/8–5/4–11/8–3/2–13/8–7/4–15/8 \\ 1–12/11–6/5–4/3–3/2–8/5–12/7–24/13 }[/math]
The fully extended chord can use even more extensions without breaking its logic. It is just that the identities of higher harmonics get progressively weaker, until vanishing in the sea of harmonic entropy. The ultra-extended contruction of the chord includes an extra segment on the two octaves, with harmonics as high as the 23rd. Arguably, it is really on the edge. Bordering on the average JND of human beings, the difference between 21/20 and 22/21 is subtle enough, not to mention what is implied by the 23rd harmonic. The chord would be
[math]\displaystyle{ \displaystyle 1–5/4–3/2–7/4–9/4–11/4–13/4–15/4–17/4|19/4–21/4|23/4 \\ 1–6/5–3/2–12/7–24/11–8/3–16/5–48/13–96/23|32/7–96/19|96/17 }[/math]
where the pipe denotes alternative denial (logical NAND). While the segment has four tones, one should select two of them in light of the aesthetics of tertian harmony, although all of them could be present in the supercompact voicing.
Or it can use less. Cutting off the second octave, the harmonic seventh chord and the harmonic sixth chord are
[math]\displaystyle{ \displaystyle 1–5/4–3/2–7/4 \\ 1–6/5–3/2–12/7 }[/math]
Chapter III. Primodality and Nonrooted Chord Construction
Chapter IV. Diminished Chords and Augmented Chords
| Interval Category Characteristics |
Layer of Tonality |
Contrasting Pair Examples |
|---|---|---|
| Pivotal harmonics | Tonality | 5/4 vs 6/5 |
| Ambitonal harmonics | Microtonality | 11/10 vs 12/11 |
| Pseudoambitonal harmonics | Pseudotonality | 30/17 vs 17/10 |
| Pseudomicrotonality | 17/16 vs 18/17 |
Chapter V. Things Repel the Similar but not Identical




Chapter VI. Overview on Functional Harmony

Explicit Functions
Implicit Functions
Composite Functions
| Ratios | Functions |
|---|---|
| 8/7, 7/6 | Subvaricant |
| 9/7, 21/16 | Covaricant |
| 32/21, 14/9 | Covaricant |
| 7/4, 12/7 | Varicant |