Spiral chart
A spiral chart is an illustration which converts a circle of repeats of an interval in one edo into a self-similar spiral shape, so that it may be compared with a circle of the same interval in a smaller coprime edo.
Spiral charts were invented by Kite Giedraitis no later than 2019.
Spirals of twelve fifths
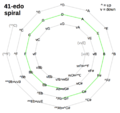
The spiral charts for 31edo, 41edo and 53edo relate each of those edos to 12edo. Each chart has 12 wheel-spokes.
The larger edo's spiral of fifths is not really a spiral, it's a larger circle that you break into a chain and make a bunch of smaller 12-note loops with. Then add a few duplicates at each end of the chain, so that you can reconnect the ends mentally and get the original larger circle.
A 12-spoke spiral chart of fifths is only possible if the dodeca-sharpness (edosteps per Pythagorean comma) of the larger edo is 1 or -1.
Gallery
-
31edo spiral chart -
41edo spiral chart -
41edo spiral chart (notation) -
53edo spiral chart
Spirals of other amounts, other intervals
Such a spiral chart can be made for any two edos, as long as they are coprime. It's often a spiral of something other than fifths. In fact, it's a spiral of the nearest miss.
For example, consider 8edo and 27edo. The near misses are 3\8 and 10\27. You get an 8-spoke spiral of 27edo major 3rds. This might be useful for someone researching octatonic scales in 27edo.
Relationship to the scale tree
|
Todo: complete section |