Oneirotonic
The term oneirotonic (/oʊnaɪrəˈtɒnɪk/ oh-ny-rə-TON-ik or /ənaɪrə-/ ə-ny-rə-) is used for the 8-note MOS structure 5L 3s, whose brightest mode is LLsLLsLs. The name "oneirotonic" was coined by Cryptic Ruse after the Dreamlands in H.P. Lovecraft's Dream Cycle mythos. Oneirotonic is a distorted diatonic, because it has one extra small step compared to diatonic (5L 2s).
The generator size ranges from 450¢ (3\8) to 480¢ (2\5). Hence any edo with an interval between 450¢ and 480¢ has an oneirotonic scale. 13edo is the smallest edo with a (non-degenerate) 5L3s oneirotonic scale and thus is the most commonly used oneirotonic tuning.
In terms of regular temperaments, there are at least two melodically viable ways to interpret oneirotonic. 13edo represents both temperaments.
- When the generator is between 461.54¢ (5\13) and 466.67¢ (7\18): A-Team (13&18, a 4:5:9:21 or 2.9.5.21 temperament)
- When the generator is between 457.14¢ (8\21) and 461.54¢ (5\13): Petrtri (13&21, a 4:5:9:11:13:17 or 2.5.9.11.13.17 temperament)
Notation
The notation used in this article is J Celephaïsian (LsLLsLLs) = JKLMNOPQJ (with J ≈ 180 Hz), unless specified otherwise.
Intervals
| Generators | Notation (1/1 = J) | Octatonic interval category name | Generators | Notation of 2/1 inverse | Octatonic interval category name |
|---|---|---|---|---|---|
| The "diatonic" 8-note scale has the following intervals (from some root): | |||||
| 0 | J | perfect unison | 0 | J | octave |
| 1 | M | perfect mosfourth | -1 | O | perfect mossixth |
| 2 | P | major mosseventh | -2 | L | minor mosthird |
| 3 | K | major mossecond | -3 | Qb | minor moseighth |
| 4 | N | major mosfifth | -4 | Nb | minor mosfifth |
| 5 | Q | major moseighth | -5 | Kb | minor mossecond |
| 6 | L# | major mosthird | -6 | Pb | minor mosseventh |
| 7 | O# | augmented sixth | -7 | Mb | diminished fourth |
| The "chromatic" 13-note scale also has the following intervals (from some root): | |||||
| 8 | J# | augmented unison | -8 | Jb | diminished octave |
| 9 | M# | augmented mosfourth | -9 | Ob | diminished mossixth |
| 10 | P# | augmented mosseventh | -10 | Lb | diminished mosthird |
| 11 | K# | augmented mossecond | -11 | Qbb | diminished moseighth |
| 12 | N# | augmented mosfifth | -12 | Nbb | diminished mosfifth |
Oneirotonic key signatures
Flat keys:
- Jb Celephaisian, Lb Dylathian = Qb, Nb, Kb, Pb, Mb, Jb, Ob, Lb
- Mb Celephaisian, Ob Dylathian = Qb, Nb, Kb, Pb, Mb, Jb, Ob
- Pb Celephaisian, Jb Dylathian = Qb, Nb, Kb, Pb, Mb, Jb
- Kb Celephaisian, Mb Dylathian = Qb, Nb, Kb, Pb, Mb
- Nb Celephaisian, Pb Dylathian = Qb, Nb, Kb, Pb
- Qb Celephaisian, Kb Dylathian = Qb, Nb, Kb
- L Celephaisian, Nb Dylathian = Qb, Nb
- O Celephaisian, Qb Dylathian = Qb
All-natural key signature:
- J Celephaisian, L Dylathian = no sharps or flats
Sharp keys:
- M Celephaisian, O Dylathian = L#
- P Celephaisian, J Dylathian = L#, O#
- K Celephaisian, M Dylathian = L#, O#, J#
- N Celephaisian, P Dylathian = L#, O#, J#, M#
- Q Celephaisian, K Dylathian = L#, O#, J#, M#, P#
- Enharmonic with Jb Celeph., Lb Dylath. in 13edo
- L# Celephaisian, N Dylathian = L#, O#, J#, M#, P#, K#
- Enharmonic with Mb Celeph., Ob Dylath. in 13edo
- O# Celephaisian, Q Dylathian = L#, O#, J#, M#, P#, K#, N#
- Enharmonic with Pb Celeph., Jb Dylath. in 13edo
- J# Celephaisian, L# Dylathian = L#, O#, J#, M#, P#, K#, N#, Q#
- Enharmonic with Kb Celeph., Mb Dylath. in 13edo
J/Q# J#/Kb K/Lb K#/L L#/Mb M M#/Nb N N#/Ob O O#/Pb P P#/Qb Q/Jb J/Q#
Modal harmony
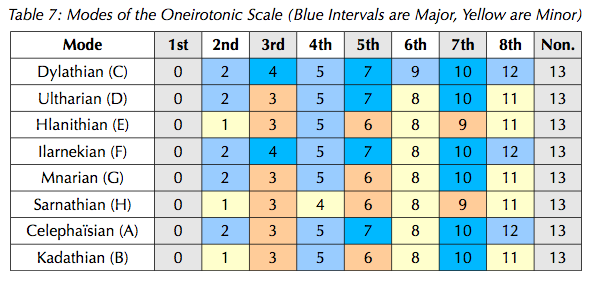
Oneirotonic modes are named after cities in the Dreamlands.
- Dylathian: LLsLLsLs (major with hints of Mixolydian and "#5")
- Ilarnekian: LLsLsLLs (major with hints of "b6")
- Celephaïsian: LsLLsLLs (the oneirotonic melodic minor. Very classical-sounding; Easley Blackwood's 13-note etude uses this as its home mode.)
- Ultharian: LsLLsLsL (A Dorian analogue. Another Dorian analogue is the MODMOS LsLLLsLs)
- Mnarian: LsLsLLsL
- Kadathian: sLLsLLsL (another "Locrian")
- Hlanithian: sLLsLsLL (closest Locrian analogue)
- Sarnathian: sLsLLsLL (Darkest but ironically the most consonant. Here be dragons.)
The modes in 13edo edo steps and C-H notation:
Modes with sharp tritone
At least in A-Team, the brighter modes can be viewed as providing a distorted version of diatonic functional harmony. For example, in the Dylathian mode, the 4:5:9 triad on the sixth degree can sound like both "V" and "III of iv" depending on context. Basic chord progressions can move by minor fourths, thirds, or major seconds: for example, J major-M minor-P minor-Ob major-J major (in Ilarnekian) or J major-K major-O major-M major-J major (in Dylathian).
Modes with flat tritone
The darker modes are radically different in character than the brighter modes. Because of the consonant 11/8 minor tritone and the 13/8 minor sixth, the flat tritone sounds more like a stable scale function.
A-Team (13&18, 4:5:9:(11:13):21) interpretation
EDOs that support A-Team include 13edo, 18edo, 31edo and 44edo.
It is possible to tune A-Team by ear, by tuning a chain of pure harmonic sevenths and taking every other note. This corresponds to using a generator of 64/49 = 462.34819 cents. A chain of fourteen 7/4's are needed to tune the 8-note oneirotonic MOS.
The sizes of the generator, large step and small step of oneirotonic are as follows in various A-Team tunings.
| 13edo | 18edo | 31edo | 64/49 generator | JI intervals represented (2.9.5.21 subgroup) | |
|---|---|---|---|---|---|
| generator | 5\13, 461.54 | 7\18, 466.67 | 12\31, 464.52 | 462.35 | 21/16 |
| L | 2\13, 184.62 | 3\18, 200.00 | 5\31, 193.55 | 187.04 | 9/8, 10/9 |
| s | 1\13, 92.31 | 1\18, 66.66 | 2\31, 77.42 | 88.26 | 21/20 |
Intervals
Sortable table of Dylathian, the brightest mode:
| Degree | Size in 13edo | Size in 18edo | Size in 31edo | Note name on J | Approximate ratios[1] | #Gens up |
|---|---|---|---|---|---|---|
| 1 | 0\13, 0.00 | 0\18, 0.00 | 0\31, 0.00 | J | 1/1 | 0 |
| 2 | 2\13, 184.62 | 3\18, 200.00 | 5\31, 193.55 | K | 9/8, 10/9 | +3 |
| 3 | 4\13, 369.23 | 6\18, 400.00 | 10\31, 387.10 | L | 5/4 | +6 |
| 4 | 5\13, 461.54 | 7\18, 466.67 | 12\31, 464.52 | M | 21/16, 13/10 | +1 |
| 5 | 7\13, 646.15 | 10\18, 666.66 | 17\31, 658.06 | N | 13/9, 16/11 | +4 |
| 6 | 9\13, 830.77 | 13\18, 866.66 | 22\31, 851.61 | O | 13/8, 18/11 | +7 |
| 7 | 10\13, 923.08 | 14\18, 933.33 | 24\31, 929.03 | P | 12/7 | +2 |
| 8 | 12\13, 1107.69 | 17\18, 1133.33 | 29\31, 1122.58 | Q | +5 |
- ↑ The harmonics over 1/1 are in bold. The ratio interpretations that are not valid for 18edo are italicized.
Petrtri (13&21, 4:5:9:11:13:17) interpretation
The sizes of the generator, large step and small step of oneirotonic are as follows in various Petrtri tunings. (Golden oneirotonic uses 1200*(2-φ) = 458.3592135¢ as generator and has L/s = φ; it is the limit of taking generators in Fibonacci number edos 5\13, 8\21, 13\34, 21\55, 34\89,....)
| 13edo | 21edo | 34edo | Golden oneirotonic | JI intervals represented (2.5.9.11.13.17 subgroup) | |
|---|---|---|---|---|---|
| generator (g) | 5\13, 461.54 | 8\21, 457.14 | 13\34, 458.82 | 458.36 | 13/10, 17/13, 22/17 |
| L (3g - octave) | 2\13, 184.62 | 3\21, 171.43 | 5\34, 176.47 | 175.08 | 10/9, 11/10 |
| s (-5g + 2 octaves) | 1\13, 92.31 | 2\21, 114.29 | 3\34, 105.88 | 108.20 | 18/17, 17/16 |
Intervals
Sortable table of Dylathian, the brightest mode:
| Degree | Size in 13edo | Size in 21edo | Size in 34edo | Note name on J | Approximate ratios | #Gens up |
|---|---|---|---|---|---|---|
| 1 | 0\13, 0.00 | 0\21, 0.00 | 0\34, 0.00 | J | 1/1 | 0 |
| 2 | 2\13, 184.62 | 3\21, 171.43 | 5\34, 176.47 | K | 10/9, 11/10 | +3 |
| 3 | 4\13, 369.23 | 6\21, 342.86 | 10\34, 352.94 | L | 11/9, 16/13 | +6 |
| 4 | 5\13, 461.54 | 8\21, 457.14 | 13\34, 458.82 | M | 13/10, 17/13, 22/17 | +1 |
| 5 | 7\13, 646.15 | 11\21, 628.57 | 18\34, 635.294 | N | 13/9, 16/11 | +4 |
| 6 | 9\13, 830.77 | 14\21, 800.00 | 23\34, 811.77 | O | 8/5 | +7 |
| 7 | 10\13, 923.08 | 16\21, 914.29 | 26\34, 917.65 | P | 17/10 | +2 |
| 8 | 12\13, 1107.69 | 19\21, 1085.71 | 31\34, 1094.12 | Q | 17/9, 32/17 | +5 |
Chords
The pentad P1-m8-M10-m12-M16 "5:9:11:13:17" occurs twice in the 8 note mos of 13edo and 21edo's father[8]. The pentad P1-M3-M4-m6-m9 "4:5:11:13:17" occurs once.
Triad occurrences:
- P1-M2-M3 "9:10:11" occurs 2x
- P1-M2-M5 "9:10:13" occurs 3x
- P1-M2-M8 "9:10:17" occurs 3x
- P1-M3-M5 "9:11:13" occurs 2x
- P1-M3-M8 "9:11:17" occurs 2x
- P1-M5-M8 "9:13:17" occurs 3x
All 8 modes provide chords in various prime families (list of modes is non-exhaustive):
- /2 chords occur on Sarnathian
- /5 chords occur on Ultharian and Mnarian
- /9 chords occur on Dylathian and Ilarnekian
- /11 chords occur on Hlanithian and Sarnathian
- /13 chords occur on Mnarian and Kadathian
- /17 chords occur on Hlanithian and Kadathian
Samples
(A rather classical-sounding 3-part harmonization of the ascending J Ilarnekian scale; tuning is 13edo)
(13edo, first 30 seconds is in Celephaïsian mode)
(13edo, Ilarnekian)
(by Igliashon Jones, 13edo, Celephaïsian)