5L 3s

5L 3s refers to the structure of MOS scales with generators ranging from 2\5 (two degrees of 5edo = 480¢) to 3\8 (three degrees of 8edo = 450¢). In the case of 8edo, L and s are the same size; in the case of 5edo, s becomes so small it disappears (and all that remains are the five equal L's).

The term oneirotonic (/oʊnaɪrəˈtɒnɪk/ oh-ny-rə-TON-ik or /ənaɪrə-/ ə-ny-rə-) is often used for the octave-equivalent MOS structure 5L 3s, whose brightest mode is LLsLLsLs. The name oneirotonic (from Greek oneiros 'dream') was coined by Cryptic Ruse after the Dreamlands in H.P. Lovecraft's Dream Cycle mythos. Oneirotonic is a distorted diatonic, because it has one extra small step compared to diatonic (5L 2s).

The generator size ranges from 450¢ (3\8) to 480¢ (2\5). Hence any edo with an interval between 450¢ and 480¢ has an oneirotonic scale. 13edo is the smallest edo with a (non-degenerate) 5L3s oneirotonic scale and thus is the most commonly used oneirotonic tuning.

In terms of regular temperaments, there are at least two melodically viable ways to interpret oneirotonic (analogous to diatonic having multiple temperament interpretations depending on generator size):

1. When the generator is between 461.54¢ (5\13) and 466.67¢ (7\18): A-Team (13&18, a 4:5:9:21 or 2.9.5.21 temperament)
2. When the generator is between 457.14¢ (8\21) and 461.54¢ (5\13): Petrtri (13&21, a 4:5:9:11:13:17 or 2.5.9.11.13.17 temperament)

13edo represents both temperaments.

More extreme oneirotonic temperaments include:

• Tridec (a 5:7:11:13 or 2.7/5.11/5.13/5 subgroup temperament), when the generator is between 454.05c (14\37) and 457.14c (8\21). These have a L/s ratio of 5/4 to 3/2.
• Buzzard, when the generator is between 471.42¢ (11\28) and 480¢ (2\5). While this is a harmonically accurate temperament, with 4 generators reaching 3/2 and -3 generators 7/4, it is relatively weak melodically, as the optimum size of the small steps is around 20-25 cents, making it difficult to distinguish from equal pentatonic.

Scale tree

generator					tetrachord	g in cents	2g	3g	4g	Comments
2\5					1 0 1	480.000	960.000	240.00	720.000
21\53					10 1 10	475.472	950.943	226.415	701.887	Vulture/Buzzard is around here
19\48					9 1 9	475	950	225	700
17\43					8 1 8	474.419	948.837	223.256	697.674
15\38					7 1 7	473.684	947.368	221.053	694.737
13\33					6 1 6	472.727	945.455	218.181	690.909
11\28					5 1 5	471.429	942.857	214.286	685.714
9\23					4 1 4	469.565	939.130	208.696	678.261	L/s = 4
7\18					3 1 3	466.667	933.333	200.000	666.667	L/s = 3 A-Team starts around here...
	19\49				8 3 8	465.306	930.612	195.918	661.2245
		50\129			21 8 21	465.116	930.233	195.349	660.465
			131\338		55 21 55	465.089	930.1775	195.266	660.335
				212\547	89 34 89	465.082	930.1645	195.247	660.329
			81\209		34 13 34	465.072	930.1435	195.215	660.287
		31\80			13 5 13	465	930	195	660
	12\31				5 2 5	464.516	929.032	193.549	658.065
5\13					2 1 2	461.538	923.077	184.615	646.154	...and ends here Boundary of propriety (generators smaller than this are proper) Petrtri starts here...
	13\34				5 3 5	458.824	917.647	176.471	635.294
		34\89			13 8 13	458.427	916.854	175.281	633.708
			89\233		34 21 34	458.369	916.738	175.107	633.473
				233\610	89 55 89	458.361	916.721	175.082	633.443	Golden father; generator is 2 octaves minus logarithmic phi
			144\377		55 34 55	458.355	916.711	175.066	633.422
		55\144			21 13 21	458.333	916.666	175	633.333
	21\55				8 5 8	458.182	916.364	174.545	632.727
8\21					3 2 3	457.143	914.286	171.429	628.571	...and ends here Optimum rank range (L/s=3/2) father
11\29					4 3 4	455.172	910.345	165.517	620.690	Tridec is around here
14\37					5 4 5	454.054	908.108	162.162	616.216
17\45					6 5 6	453.333	906.667	160	613.333
20\53					7 6 7	452.83	905.66	158.491	611.321
23\61					8 7 8	452.459	904.918	157.377	609.836
26\69					9 8 9	452.174	904.348	156.522	608.696
29\77					10 9 10	451.948	903.896	155.844	607.792
3\8					1 1 1	450.000	900.000	150.000	600.000

Tuning ranges and data

A-Team (13&18)

A-Team tunings (with generator between 5\13 and 7\18) have L/s ratios between 2/1 and 3/1.

EDOs that support A-Team include 13edo, 18edo, and 31edo.

• 18edo can be used for a large L/s ratio of 3, (thus 18edo oneirotonic is distorted 17edo diatonic), or for nearly pure 9/8 and 7/6.
• 31edo can be used to make the major mos3rd a near-just 5/4.

The sizes of the generator, large step and small step of oneirotonic are as follows in various A-Team tunings.

	13edo	18edo	31edo	Optimal (POTE) tuning	JI intervals represented (2.9.5.21 subgroup)
generator (g)	5\13, 461.54	7\18, 466.67	12\31, 464.52	464.14	21/16
L (3g - octave)	2\13, 184.62	3\18, 200.00	5\31, 193.55	192.42	9/8, 10/9
s (-5g + 2 octaves)	1\13, 92.31	1\18, 66.66	2\31, 77.42	79.30	21/20

Trivia: A-Team can be tuned by ear, by tuning a chain of pure harmonic sevenths and taking every other note. This corresponds to using a generator of 64/49 = 462.34819 cents. A chain of fourteen 7/4's are needed to tune the 8-note oneirotonic MOS. This produces a tuning close to 13edo.

Petrtri (13&21)

Petrtri tunings (with generator between 8\21 and 5\13) have less extreme L-to-s ratios than A-Team tunings, between 3/2 and 2/1. The 8\21-to-5\13 range of oneirotonic tunings remains relatively unexplored.

The three major edos in this range, 13edo, 21edo and 34edo, all nominally support petrtri, but 34edo is close to optimal for the temperament, with a generator only .33c flat of the optimal (POTE) petrtri generator of 459.1502c. Close-to-optimal petrtri tunings such as 34edo may be particularly useful for the Sarnathian mode, as Sarnathian in these tunings uniquely approximates four over-2 harmonics plausibly, namely 17/16, 5/4, 11/8, and 13/8.

The sizes of the generator, large step and small step of oneirotonic are as follows in various petrtri tunings.

	13edo	21edo	34edo	Optimal (POTE) tuning	JI intervals represented (2.5.9.11.13.17 subgroup)
generator (g)	5\13, 461.54	8\21, 457.14	13\34, 458.82	459.15	13/10, 17/13, 22/17
L (3g - octave)	2\13, 184.62	3\21, 171.43	5\34, 176.47	177.45	10/9, 11/10
s (-5g + 2 octaves)	1\13, 92.31	2\21, 114.29	3\34, 105.88	104.25	18/17, 17/16

Notation

The notation used in this article is J Celephaïsian (LsLLsLLs) = JKLMNOPQJ, with reference pitch J = 360 Hz, unless specified otherwise. We denote raising and lowering by a chroma (L-s) by & "amp" and @ "at". (Mnemonics: & "and" means additional pitch. @ "at" rhymes with "flat".)

Thus the 13edo gamut is as follows:

J J&/K@ K L L&/M@ M M&/N@ N O O&/P@ P P&/Q@ Q J

Note: N is close to standard C, since the reference pitch 360 Hz for J was chosen to be nearly a pure 11/8 above standard 12edo C.

Intervals

Generators	Notation (1/1 = J)	Octatonic interval category name	Generators	Notation of 2/1 inverse	Octatonic interval category name
The 8-note MOS has the following intervals (from some root):
0	J	perfect unison	0	J	octave
1	M	perfect mosfourth	-1	O	perfect mossixth (aka major fifth)
2	P	major mosseventh	-2	L	minor mosthird
3	K	major mossecond	-3	Q@	minor moseighth
4	N	major mosfifth (aka minor fifth)	-4	N@	minor mosfifth
5	Q	major moseighth	-5	K@	minor mossecond
6	L&	major mosthird	-6	P@	minor mosseventh
7	O&	augmented sixth	-7	M@	diminished fourth
The chromatic 13-note MOS also has the following intervals (from some root):
8	J&	augmented unison	-8	J@	diminished octave
9	M&	augmented mosfourth	-9	O@	diminished mossixth
10	P&	augmented mosseventh	-10	L@	diminished mosthird
11	K&	augmented mossecond	-11	Q@@	diminished moseighth
12	N&	augmented mosfifth	-12	N@@	diminished mosfifth

Key signatures

Flat keys:

• J@ Celephaïsian, L@ Dylathian = Q@, N@, K@, P@, M@, J@, O@, L@
• M@ Celephaïsian, O@ Dylathian = Q@, N@, K@, P@, M@, J@, O@
• P@ Celephaïsian, J@ Dylathian = Q@, N@, K@, P@, M@, J@
• K@ Celephaïsian, M@ Dylathian = Q@, N@, K@, P@, M@
• N@ Celephaïsian, P@ Dylathian = Q@, N@, K@, P@
• Q@ Celephaïsian, K@ Dylathian = Q@, N@, K@
• L Celephaïsian, N@ Dylathian = Q@, N@
• O Celephaïsian, Q@ Dylathian = Q@

All-natural key signature:

• J Celephaïsian, L Dylathian = no sharps or flats

Sharp keys:

• M Celephaïsian, O Dylathian = L&
• P Celephaïsian, J Dylathian = L&, O&
• K Celephaïsian, M Dylathian = L&, O&, J&
• N Celephaïsian, P Dylathian = L&, O&, J&, M&
• Q Celephaïsian, K Dylathian = L&, O&, J&, M&, P&
  • Enharmonic with J@ Celeph., L@ Dylath. in 13edo
• L& Celephaïsian, N Dylathian = L&, O&, J&, M&, P&, K&
  • Enharmonic with M@ Celeph., O@ Dylath. in 13edo
• O& Celephaïsian, Q Dylathian = L&, O&, J&, M&, P&, K&, N&
  • Enharmonic with P@ Celeph., J@ Dylath. in 13edo
• J& Celephaïsian, L& Dylathian = L&, O&, J&, M&, P&, K&, N&, Q&
  • Enharmonic with K@ Celeph., M@ Dylath. in 13edo

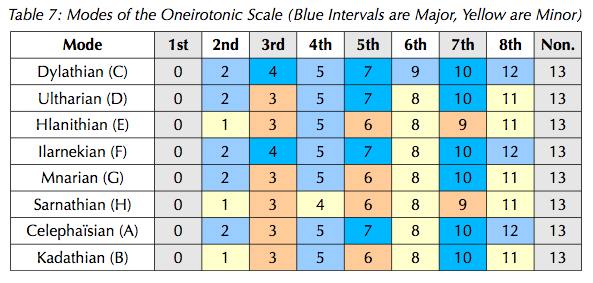
Modes

Oneirotonic modes are named after cities in the Dreamlands.

1. Dylathian: LLSLLSLS
2. Ilarnekian: LLSLSLLS
3. Celephaïsian: LSLLSLLS (Easley Blackwood's 13-note etude uses this as its home mode.)
4. Ultharian: LSLLSLSL (A kinda-sorta Dorian analogue. Depending on your purposes, a better Dorian analogue may be the MODMOS LSLLLSLS; see the section on oneiro MODMOSes below.)
5. Mnarian: LSLSLLSL
6. Kadathian: SLLSLLSL
7. Hlanithian: SLLSLSLL
8. Sarnathian: SLSLLSLL

The modes on the white keys JKLMNOPQJ are:

• J Celephaïsian
• K Kadathian
• L Dylathian
• M Ultharian
• N Hlanithian
• O Ilarnekian
• P Mnarian
• Q Sarnathian

The modes in 13edo edo steps and C-H notation:

Pseudo-diatonic theory

Oneirotonic is often used as distorted diatonic. Because distorted diatonic modal harmony and functional harmony both benefit from a recognizable major third, the following theory essentially assumes an A-Team tuning, i.e. an oneirotonic tuning with generator between 5\13 and 7\18 (or possibly an approximation of such a tuning, such as a neji). The reader is encouraged to experiment and see what ideas work for other oneirotonic tunings.

Ana modes

We call modes with a major mos5th ana modes (from Greek for 'up'), because the sharper 5th degree functions as a flattened melodic fifth when moving from the tonic up. The ana modes of the MOS are the 4 brightest modes, namely Dylathian, Ilarnekian, Celephaïsian and Ultharian.

The ana modes have squashed versions of the classical major and minor pentachords R-M2-M3-P4-P5 and R-M2-m3-P4-P5 and can be viewed as providing a distorted version of classical diatonic functional harmony. For example, in the Dylathian mode, the 4:5:9 triad on the sixth degree can sound like both "V" and "III of iv" depending on context.

In pseudo-classical functional harmony, the 6th scale degree (either an augmented mossixth or a perfect mossixth) could be treated as mutable. The perfect mossixth would be used when invoking the diatonic V-to-I trope by modulating by a perfect mosfourth from the sixth degree "dominant". The augmented mossixth would be used when a major key needs to be used on the fourth degree "subdominant".

Progressions

Some suggested basic ana functional harmony progressions, outlined very roughly (note: VI is the sharp 5th, etc.). "I" means either Imaj or Imin. "Natural" Roman numerals follow the Ilarnekian mode.

• I-IVmin-VImaj-I
• Imaj-VIImin-IVmaj-Imaj
• Imin-@IIImaj-VImaj-Imaj
• Imin-@IIImaj-Vdim-VImaj-Imin
• Imin-@VIIImin-IIImaj-VImaj-Imin
• Imin-IVmin-@VIIImin-@IIImaj-VImaj-Imin
• Imin-IVmin-IIdim-VImaj-Imin
• Imin-IVmin-IIdim-@IIImaj-Imin
• I-VIImin-IImin-VImaj-I
• Imaj-VIImin-IVmin-VImaj-Imaj
• Modulations by major mos2nd:
  • I-IV-VII-II
  • I-IVmaj-II
  • I-VIImin-II
• Modulations by major mos3rd:
  • Modulate up major mos2nd twice
  • Imin-VImin-III (only in 13edo)
  • Imaj-&VImin-III (only in 13edo)
• Modulations by minor mos3rd:
  • I-VI-@III
  • I-IVmin-VImin-@VIIImaj-@III

Another approach to oneirotonic chord progressions is to let the harmony emerge from counterpoint.

Kata modes

We call modes with a minor mos5th kata modes (from Greek for 'down'). The kata modes of the MOS are the 4 darkest modes, namely Mnarian, Kadathian, Hlanithian and Sarnathian. In kata modes, the melodically squashed fifth from the tonic downwards is the flatter 5th degree. Kata modes could be used to distort diatonic tropes that start from the tonic and work downwards or work upwards towards the tonic from below it. For example:

• Mnarian (LSLSLLSL) and Kadathian (SLLSLLSL) are kata-Mixolydians
• Hlanithian (SLLSLSLL) is a kata-melodic major (the 4th degree sounds like a major third; it's actually a perfect mosfourth.)
• Sarnathian (SLSLLSLL) is a kata-melodic minor (When starting from the octave above, the 4th degree sounds like a minor third; it's actually a diminished mosfourth.)

When used in an "ana" way, the kata modes are radically different in character than the brighter modes. Because the fifth and seventh scale degrees become the more consonant minor tritone and the minor sixth respectively, the flat tritone sounds more like a stable scale function. Hlanithian, in particular, is a lot like a more stable version of the Locrian mode in diatonic.

MODMOSes

The most important oneirotonic MODMOS is LSLLLSLS (and its rotations), because it allows one to evoke certain ana or kata diatonic modes where three whole steps in a row are important (Dorian, Phrygian, Lydian or Mixo) in an octatonic context. The MOS would not always be able to do this because it has at most two consecutive large steps. As with the MOS, this MODMOS has four ana and four kata rotations:

• LLLSLSLS: Dylathian &4: an ana-Lydian
• LLSLSLSL: Ilarnekian @8: an ana-Mixolydian
• LSLLLSLS: Celephaïsian &6: an ana-Dorian
• SLLLSLSL: Ultharian @2: an ana-Phrygian
• SLSLSLLL: Sarnathian @6: a kata-Locrian
• SLSLLLSL: Sarnathian &6: a kata-Dorian
• LSLSLLLS: Mnarian &8: a kata-Ionian
• LSLSLSLL: Hlanithian &2: a kata-Aeolian

Other potentially interesting oneirotonic MODMOSes (that do not use half-sharps or half-flats) are:

• the distorted harmonic minor LSLSLLSAS (A = aug 2nd = L + chroma)
• the distorted Freygish SASLSLLS

Chords

Chords are given in oneirotonic MOS interval notation. For example, M5 means major mosfifth (squashed fifth).

• R-M3-M5: Squashed Major Triad
• R-m3-M5: Squashed Minor Triad
• R-m3-m5: Squashed Dim Triad
• R-M3-A5: Squashed Aug Triad
• R-M3-M5-A6: Squashed Major Triad Add6
• R-m3-M5-A6: Squashed Minor Triad Add6
• R-M3-M5-M7: Oneiro Major Tetrad
• R-m3-M5-M7: Oneiro Minor Tetrad
• R-m3-m5-M7: Oneiro Half-Diminished Tetrad
• R-m3-m5-m7: Orwell Tetrad, Oneiro Diminished Tetrad
• R-M3-A6: Squashed 1st Inversion Minor Triad
• R-m3-P6: Squashed 1st Inversion Major Triad
• R-M3-M7: 1st Inversion Squashed Minor Triad (note the order of terms!)
• R-m3-m7: 1st Inversion Squashed Major Triad
• R-m5-M7: 2nd Inversion Squashed Major Triad
• R-m5-m7: 2nd Inversion Squashed Minor Triad
• R-M3-M8: Oneiro Major Seventh
• R-m3-M8: Oneiro Minor Major Seventh
• R-M3-M7-M8: Oneiro Major Seventh Add6
• R-m3-M7-M8: Oneiro Minor Major Seventh Add6
• R-M3-P6-M8: Oneiro Major Seventh Add Major Fifth
• R-m3-P6-M8: Oneiro Minor Major Seventh Add Major Fifth
• R-M3-(M2): Oneiro Major Add9
• R-m3-(M2): Oneiro Minor Add9
• R-M3-(M2)-(P4): Oneiro Major Add9 Sub11
• R-m3-(M2)-(P4): Oneiro Minor Add9 Sub11
• R-M2-P4: Squashed Sus24 No5
• R-M2-M5: Squashed Sus2 Triad
• R-P4-M5: Squashed Sus4 Triad; Naiadic Maj2
• R-M2-P4-M5: Squashed Sus24
• R-P4-M7: Oneiro Quartal Triad
• R-P4-M7-(M2): Oneiro Quartal Tetrad, Core Tetrad
• R-P4-M7-(M2)-(M5): Oneiro Quartal Pentad, Core Pentad
• R-P4-M7-(M2)-(M5)-(M8): Oneiro Quartal Hexad
• R-P4-M7-M8: Oneiro Quartal Seventh Tetrad
• R-M3-m7: Sephiroth Triad (approximates 8:10:13 in 13edo)
• R-M3-m7-m2-(P4): Sephiroth Triad Addmin9 Sub11
• R-M3-m7-(P4): Sephiroth Triad Sub11
• R-P4-m8: Expanding Quartal Triad
• R-m3-P4-m8: Expanding Quartal Triad Addm3
• R-m5-m8: Contracting Quartal Triad
• R-m5-m7-m8: Contracting Quartal Triad Addm7

Zheanist theory

A-Team oneirotonic may be a particularly good place to bring to bear Zheanism's high harmonic series chords, as A-Team temperament doesn't yield many low-complexity chords.

18edo may be a better basis for a style of oneirotonic Zheanism using comma sharp and comma flat fifths than 13edo (in particular diesis sharp and diesis flat fifths; diesis is a category with a central region of 32 to 40c). In 18edo both the major fifth (+31.4c) and the minor fifth (-35.3) are about a diesis off from a just perfect fifth. In 13edo only the major fifth is a diesis sharp, and it is +36.5c off from just; so there's less wiggle room for a neji if you want every major fifth to be at most a diesis sharp).

31nejis and 34nejis also provide opportunities to use dieses directly, since 1\31 (38.71c) and 1\34 (35.29c) are both dieses.

Primodal chords

These are just oneirotonic-inspired chords, they aren't guaranteed to fit in your neji.

/13

• 13:16:19 Tridecimal Squashed Major Triad
• 13:17:19 Tridecimal Naiadic Maj2
• 13:17:20 Tridecimal Squashed 2nd Inversion Minor Triad
• 13:17:21 Tridecimal Squashed 2nd Inversion Major Triad
• 13:16:19:22 Tridecimal Oneiro Major Tetrad
• 26:29:38 Tridecimal Squashed Sus2 Triad
• 26:29:34:38 Tridecimal Sus24

/17

• 17:20:25 Septen Squashed Minor Triad
• 17:20:26 Septen Squashed 1st Inversion Major Triad
• 17:20:25:29 Septen Minor Oneiro Tetrad
• 17:21:25:29 Septen Major Oneiro Tetrad
• 17:20:26:29 Septen Squashed 1st Inversion Major Triad addM6
• 34:40:47:55 Septen Orwell Tetrad
• 34:40:52:58:76:89:102:129 (Celephaïsian + P5; R-min3-sup5-M6-M9-sub11-P12(fc)-M14)
• 34:40:52:58:76:89:102:110:129 (Celephaïsian + P5; R-min3-sup5-M6-M9-sub11-P12(fc)-supmin13-M14)
• 34:40:50:58:89:102:129 (R-min3-sub5-M6-M9-sub11-P12(rc)-M14)
• 34:40:50:58:89:102:110:129 (R-min3-sub5-M6-M9-sub11-P12(rc)-supmin13-M14)
• 34:40:50:58:76:89:110:129 (R-m3-sub5-M6-M9-sub11-supm13-M7)
• 34:40:50:58:76:89:102:110:129:208 (R-m3-sub5-M6-M9-sub11-P12(rc)-supm13-M14-sup19(rc^2))

/23

• 23:27:30 Vice Squashed Min4 No5
• 23:27:30:35:44 Vice Squashed Min4 addM5,M7
• 23:27:37 Vice Orwell Tetrad no5
• 46:54:60:67 Vice Squashed Min4
• 46:54:63 Vice Squashed Dim
• 46:54:63:76 Vice Orwell Tetrad
• 46:54:67 Vice Squashed Min
• 46:54:67:78 Vice Minor Oneiro Tetrad
• 46:54:60:67:78 Vice Min4 Oneiro Pentad
• 46:60:67 Vice Squashed Sus4

/29

• 29:34:38 Vicenon Squashed Sus4
• 29:34:42 Vicenon Squashed Minor Triad
• 29:36:42 Vicenon Squashed Major Triad
• 29:34:40:47 Vicenon Orwell Tetrad
• 29:38:65:84:99 Vicenon Oneiro Core Pentad
• 29:38:65:84:99:110 Vicenon Oneiro Core Hexad
• 58:65:72:80:84:94:99:110:116 Vicenon Dylathian &4
• 58:65:72:76:84:94:99:110:116 Vicenon Dylathian
• 58:65:72:76:84:89:99:110:116 Vicenon Ilarnekian
• 58:65:72:76:84:89:99:104:116 Vicenon Ilarnekian @8
• 58:65:68:76:84:94:99:110:116 Vicenon Celephaïsian &6
• 58:65:68:76:84:89:99:110:116 Vicenon Celephaïsian
• 58:65:68:76:84:89:99:104:116 Vicenon Ultharian
• 58:65:68:76:80:89:99:104:116 Vicenon Mnarian
• 58:65:68:76:80:89:99:110:116 Vicenon Mnarian &8
• 58:65:68:76:80:89:94:104:116 Vicenon Hlanithian &2
• 58:61:68:76:80:89:99:104:116 Vicenon Kadathian
• 58:61:68:76:84:89:99:104:116 Vicenon Ultharian @2
• 58:61:68:76:80:89:94:104:116 Vicenon Hlanithian
• 58:61:68:72:80:89:99:104:116 Vicenon Sarnathian &6
• 58:61:68:72:80:89:94:104:116 Vicenon Sarnathian
• 58:61:68:72:80:84:94:104:116 Vicenon Sarnathian @6

Some oneirotonic nejis

• 58:61:65:68:72:76:80:84:89:94:99:104:110:116 A very low-complexity 13neji; not optimized for transposability.

"Oneirotonic maqam"

"Oneirotonic maqam" is based on the idea "If maqam is loosely an extension of diatonic that uses neutral intervals, what is the oneirotonic counterpart that uses oneirotonic neutral intervals?" or "What if we distorted maqam scales similarly to how oneirotonic distorts diatonic scales?" The following assumes an edo with A-Team oneirotonic scales and neutral mosseconds (i.e. half of an oneirotonic minor mosthird) such as 18edo and 26edo. In rank-2 temperament terms, this requires a loosely 18&26 structure.

• 26edo can be used if you want neutral mosseconds and minor mosthirds closer to their 24edo counterparts. In 26edo these are 138c and 277c respectively, but in 18edo these are 133c and 267c.
• 18edo can be used if you want neutral mosthirds (neutral mos2nd + major mos2nd) closer to conventional neutral thirds. The neutral mos3rd is 333c in 18edo and 323c in 26edo.

Oneirotonic rank-2 temperaments

The only notable harmonic entropy minimum is Vulture/Buzzard, in which four generators make a 3/1 (and three generators approximate an octave plus 8/7). The rest of this region does not approximate low-complexity JI harmony well, though there are a couple notable subgroup temperaments.

Todo: Add temperament data

A-Team (13&18, 2.5.9.21)

Sortable table of intervals in the Dylathian mode and their A-Team interpretations:

Degree	Size in 13edo	Size in 18edo	Size in 31edo	Note name on L	Approximate ratios	#Gens up
1	0\13, 0.00	0\18, 0.00	0\31, 0.00	L	1/1	0
2	2\13, 184.62	3\18, 200.00	5\31, 193.55	M	9/8, 10/9	+3
3	4\13, 369.23	6\18, 400.00	10\31, 387.10	N	5/4	+6
4	5\13, 461.54	7\18, 466.67	12\31, 464.52	O	21/16, 13/10	+1
5	7\13, 646.15	10\18, 666.66	17\31, 658.06	P	13/9, 16/11	+4
6	9\13, 830.77	13\18, 866.66	22\31, 851.61	Q	13/8, 18/11	+7
7	10\13, 923.08	14\18, 933.33	24\31, 929.03	J	12/7	+2
8	12\13, 1107.69	17\18, 1133.33	29\31, 1122.58	K		+5

Petrtri (13&21, 2.5.9.11.13.17)

Intervals

Sortable table of intervals in the Dylathian mode and their Petrtri interpretations:

Degree	Size in 13edo	Size in 21edo	Size in 34edo	Size in POTE tuning	Note name on L	Approximate ratios	#Gens up
1	0\13, 0.00	0\21, 0.00	0\34, 0.00	0.00	L	1/1	0
2	2\13, 184.62	3\21, 171.43	5\34, 176.47	177.45	M	10/9, 11/10	+3
3	4\13, 369.23	6\21, 342.86	10\34, 352.94	354.90	N	11/9, 16/13	+6
4	5\13, 461.54	8\21, 457.14	13\34, 458.82	459.15	O	13/10, 17/13, 22/17	+1
5	7\13, 646.15	11\21, 628.57	18\34, 635.294	636.60	P	13/9, 16/11	+4
6	9\13, 830.77	14\21, 800.00	23\34, 811.77	814.05	Q	8/5	+7
7	10\13, 923.08	16\21, 914.29	26\34, 917.65	918.30	J	17/10	+2
8	12\13, 1107.69	19\21, 1085.71	31\34, 1094.12	1095.75	K	17/9, 32/17	+5

Buzzard (48&53, 2.3.5.7)

Commas: 1728/1715, 5120/5103

POTE generator: ~320/243 = 475.636

Map: [<1 0 -6 4|, <0 4 21 -3|]

Wedgie: <<4 21 -3 24 -16 -66||

EDOs: 48, 53, 111, 164d, 275d

Badness: 0.0480

Samples (for oneirotonic)

‎(A rather classical-sounding 3-part harmonization of the ascending J Ilarnekian scale; tuning is 13edo)

(13edo, first 30 seconds is in J Celephaïsian)

(13edo, L Ilarnekian)

(by Igliashon Jones, 13edo, J Celephaïsian)

Tritave MOSes with the 5L 3s pattern

By a weird coincidence, the other generator for this MOS will generate the same pattern within a tritave equivalence. By yet another weird coincidence, this MOS belongs to a temperament which has Bohlen-Pierce as its index-2 subtemperament. In addition to being harmonious, this tuning of the MOS gives an L/s ratio between 3/1 and 3/2, which is squarely in the middle of the range, being thus neither too exaggerated nor too equalized to be recognizable as such, unlike in octaves, where the only notable harmonic entropy minimum is near a greatly exaggerated 10/1 L/s ratio.

\					tetrachord	g in cents hekts	2g	3g	4g	Comments
2\5					1 0 1	760.782 520	1521.564 1040	380.391 260	1141.173 780
27\68					13 1 13	755.188 516.1765	1510.376 1032.353	363.609 248.529	1118.797 764.706	2g=12/5 minus quarter comma near here
25\63					12 1 12	754.744 515.873	1509.488 1031.746	362.277 247.619	1117.021 763.492
23\58					11 1 11	754.2235 515.517	1508.447 1031.0345	360.716 246.551	1114.939 762.069
21\53					10 1 10	753.605 515.094	1507.21 1030.189	358.859 245.283	1112.464 760.378
19\48					9 1 9	752.857 514.583	1505.714 1029.167	356.617 243.75	1109.474 758.333
17\43					8 1 8	751.936 513.9535	1503.871 1027.907	353.852 241.8605	1105.788 755.814
15\38					7 1 7	750.771 513.158	1501.543 1026.316	350.36 239.474	1101.132 752.632
	28/71				13 2 13	750.067 512.676	1500.1335 1025.352	348.245 238.028	1098.312 750.704
	41\104				19 3 19	749.809 512.5	1499.618 1025	347.4725 237.5	1097.282 750	3g=11/3 near here
13\33					6 1 6	749.255 512.121	1498.51 1024.242	345.81 236.364	1095.065 748.485
	24\61				11 2 11	748.31 511.475	1496.62 1022.951	342.976 234.426	1091.286 745.902
	35\89				16 3 16	747.96 511.236	1495.92 1022.472	341.924 233.708	1089.884 744.944
					5+√29 2 5+√29	747.648 511.023	1495.297 1022.046	340.99 233.069	1088.638 744.092	4g=45/8 near here
11\28					5 1 5	747.197 510.714	1494.393 1021.429	339.635 232.143	1086.831 742.857
	20\51				9 2 9	745.865 509.804	1491.729 1019.608	335.639 229.412	1081.504 739.216
	29\74				13 3 13	745.361 509.4595	1490.721 1018.919	334.127 228.378	1079.488 737.838
	38/97				17 4 17	745.096 509.278	1490.192 1018.557	333.332 227.835	1078.428 737.113
					2+√5 1 2+√5	754.051 509.2475	1490.101 1018.495	333.197 227.742	1078.247 736.99
	47\120				21 5 21	744.932 509.167	1489.865 1018.333	332.842 227.5	1077.7745 736.667
9\23					4 1 4	744.243 508.696	1488.487 1017.391	330.775 226.087	1075.018 734.783	L/s = 4
	34\87				15 4 15	743.293 508.046	1486.586 1016.092	327.923 224.138	1071.216 732.184	4g=39/7 near here
	25\64				11 3 11	742.951 507.8125	1485.902 1015.625	326.899 223.4375	1069.85 731.25
	16\41				7 2 7	742.226 507.317	1484.453 1014.634	324.724 221.951	1066.95 728.268
	23\59				10 3 10	741.44 506.78	1482.88 1013.56	322.365 220.34	1063.805 727.12
					3+√13 2 3+√13	741.289 506.676	1482.577 1013.352	321.911 220.028	1063.2 726.705
	30\77				13 4 13	741.021 506.4935	1482.043 1012.987	321.109 219.4805	1062.131 725.974
					pi 1 pi	740.449 506.102	1480.898 1012.204	319.392 218.3065	1056.841 724.409	L/s = pi
7\18					3 1 3	739.649 505.556	1479.298 1011.111	316.992 216.667	1056.642 722.222	L/s = 3
	68\175				29 10 29	739.045 505.143	1478.091 1010.286	315.181 215.429	1054.227 720.571	3g=18/5 near here
	61/157				26 9 26	738.976 505.0955	1477.952 1010.191	314.973 215.287	1053.949 720.382
	54\139				23 8 23	738.889 505.036	1477.778 1010.072	314.712 215.108	1053.601 720.144
	47\121				20 7 20	738.776 504.959	1477.552 1009.917	314.373 214.876	1053.149 719.835
	40\103				17 6 17	738.623 504.854	1477.247 1009.709	313.915 214.563	1052.538 719.4175
	33\85				14 5 14	738.406 504.706	1476.812 1009.412	313.263 214.1765	1051.669 718.882
	26\67				11 4 11	738.072 504.478	1476.144 1008.955	312.261 213.433	1050.333 717.91
					e 1 e	737.855 504.329	1475.71 1008.6585	311.61 212.988	1049.465 717.317	L/s = e
	19\49				8 3 8	737.493 504.082	1474.986 1008.163	310.523 212.245	1048.016 716.3265	3g=18/5 minus quarter comma near here
		50\129			21 8 21	737.192 503.876	1474.384 1007.752	309.621 211.628	1046.812 715.504
			131\338		55 21 55	737.148 503.846	1474.296 1007.692	309.49 211.5385	1046.638 715.385
				212\547	89 34 89	737.138 503.839	1474.276 1007.678	309.459 211.517	1046.597 715.3565
			81\209		34 13 34	737.121 503.828	1474.243 1007.6555	309.409 211.483	1046.53 715.311
		31\80			13 5 13	737.008 503.75	1474.015 1007.5	309.068 211.25	1046.075 715
	12\31				5 2 5	736.241 503.226	1472.481 1006.452	306.767 209.677	1043.007 712.903
					1+√2 1 1+√2	735.542 502.748	1471.084 1005.497	304.6715 208.245	1040.214 710.994	Silver false father
	17\44				7 3 7	734.846 502.273	1469.693 1004.5455	302.584 206.818	1037.41 709.091
	22\57				9 4 9	734.088 501.754	1468.176 1003.509	300.309 205.263	1034.397 707.0175
	27\70				11 5 11	733.611 501.429	1467.222 1002.857	298.879 204.286	1032.49 705.714
	32\83				13 6 13	733.284 501.205	1466.568 1002.41	297.897 203.6145	1031.181 704.819	2g=7/3 near here
5\13					2 1 2	731.521 500	1463.042 1000	292.609 200	1024.13 700
	48\125				19 10 19	730.35 499.2	1460.701 998.4	289.097 197.6	1019.448 696.8	3g=39/11 near here
	43\112				17 9 17	730.215 499.107	1460.43 998.214	288.69 197.321	1018.905 696.429
	38\99				15 8 15	730.043 498.99	1460.087 997.98	288.175 196.97	1018.218 695.96
	33\86				13 7 13	729.82 498.837	1459.64 997.674	287.505 196.512	1017.325 695.349	4g=27/5 near here
	28\73				11 6 11	729.547 498.63	1459.034 997.26	286.596 195.89	1016.113 694.5205
	23\60				9 5 9	729.083 498.333	1458.1655 996.667	285.293 195	1014.376 693.333
		41\107			16 9 16	728.7865 498.131	1457.563 996.262	284.4045 194.3925	1013.191 692.523
		59\154			23 13 23	728.671 498.052	1457.342 996.104	284.058 194.156	1012.729 692.208	3g=99/28 near here
		77\201			30 17 30	728.61 498.01	1457.219 996.02	283.874 194.03	1012.483 692.04
		95\248			37 21 37	728.5715 497.984	1457.143 995.968	283.7145 193.952	1012.286 691.9355	Golden BP is index-2 near here
	18\47				7 4 7	728.408 497.872	1456.817 995.745	283.27 193.617	1011.678 691.49
					√3 1 √3	728.159 497.702	1456.318 995.404	282.522 193.106	1010.6815 690.808	4g=27/5 minus third comma near here
		31\81			12 7 12	727.909 497.531	1455.817 995.062	281.771 192.593	1009.68 690.1235
	13\34				5 3 5	727.218 497.059	1454.436 994.118	279.699 191.1765	1006.917 688.235
		34\89			13 8 13	726.59 496.629	1453.179 993.258	277.814 189.888	1004.403 686.517
			89\233		34 21 34	726.498 496.5665	1452.996 993.133	277.538 189.7	1004.036 686.266
				233\610	89 55 89	726.4845 496.557	1452.969 993.115	277.4985 189.672	1003.983 686.2295	Golden false father
			144\377		55 34 55	726.476 496.552	1452.952 993.104	277.473 189.655	1003.95 686.207
		55\144			21 13 21	726.441 496.528	1452.882 993.056	277.368 189.583	1003.809 686.111
	21\55				8 5 8	726.201 496.364	1452.402 992.727	276.468 189.091	1002.849 685.4545
					pi 2 pi	725.736 496.046	1451.472 992.091	275.252 188.137	1000.988 684.183
8\21					3 2 3	724.554 495.238	1449.109 990.476	271.708 185.714	996.226 680.952	Optimum rank range (L/s=3/2) false father 4g=16/3 near here
	27\71				10 7 10	723.279 494.366	1446.557 988.732	267.881 183.099	991.16 677.465
		46\121			17 12 17	723.057 494.215	1446.115 988.43	267.217 182.645	990.274 676.8595
	19\50				7 5 7	722.743 494	1445.486 988	266.274 182	989.017 676	3g=7/2 near here
11\29					4 3 4	721.431 493.103	1442.862 986.207	262.338 179.31	983.77 672.414
	25\66				9 7 9	720.4375 492.424	1440.875 984.8485	259.3575 177.273	979.795 669.697
		64\169			23 18 23	720.267 492.308	1440.534 984.615	258.848 176.923	979.113 669.231
			167\441		60 47 60	720.2415 492.29	1440.483 984.5805	258.7965 176.871	979.001 669.161
				437\1154	157 123 157	720.238 492.288	1440.475 984.575	258.758 176.863	978.996 669.151
			270\713		97 76 97	720.235 492.286	1440.471 984.572	258.751 176.858	978.987 669.1445
		103\272			37 29 37	720.226 492.279	1440.451 984.558	258.722 176.837	978.947 669.116
	39\103				14 11 14	720.158 492.233	1440.315 984.466	258.518 176.699	978.676 668.932
14\37					5 4 5	719.659 491.892	1439.317 983.784	257.021 175.676	976.679 667.568
	31\82				11 9 11	719.032 491.463	1438.064 982.927	255.14 174.39	974.172 665.844
		79\209			28 23 28	718.921 491.388	1437.842 982.775	254.807 174.163	973.728 665.55
			206\545		73 60 73	718.904 491.376	1437.808 982.752	254.757 174.138	973.661 665.505
				539\1426	191 117 191	718.902 491.3745	1437.803 982.749	254.75 174.123	973.652 665.498
			333\881		118 97 118	718.9 491.373	1437.8 982.747	254.745 174.12	973.6455 665.494
		127\336			45 37 45	718.893 491.369	1437.787 982.738	254.726 174.107	973.619 665.476
	48\127				17 14 17	718.849 491.339	1437.698 982.677	254.592 174.016	973.441 665.354
17\45					6 5 6	718.516 491.111	1437.032 982.222	253.549 173.333	972.11 664.444
20\53					7 6 7	717.719 490.566	1435.438 981.132	251.202 171.698	968.9205 662.264	4g=21/4 near here
23\61					8 7 8	717.131 490.164	1434.261 980.328	249.437 170.492	966.567 660.656
	49\130				17 15 17	716.891 490	1433.7815 980	248.717 170	965.608 660	4g=quarter-comma meantone 21/4 near here 6g=12 near here
26\69					9 8 9	716.679 489.855	1433.357 979.71	248.081 169.565	964.76 659.42
29\77					10 9 10	716.321 489.61	1432.641 979.221	247.007 168.831	963.328 658.442
32\85					11 10 11	716.03 489.412	1432.06 978.8235	246.135 168.235	962.1655 657.647
35\93					12 11 12	715.7895 489.247	1431.579 978.495	245.4135 167.742	961.203 656.989
38/101					13 12 13	715.587 489.109	1431.174 978.218	244.806 167.327	960.393 656.436	2g=16\7 near here
3\8					1 1 1	713.233 487.5	1426.466 975	237.744 162.5	950.9775 650