Limmic temperaments: Difference between revisions
m Update |
No edit summary |
||
| Line 1: | Line 1: | ||
This '''limmic temperaments''' page collects various temperaments tempering out the Pythagorean limma, [[256/243]]. As a consequence, [[3/2]] is always represented by 3\5, 720 [[cent]]s assuming pure octaves. While quite sharp, this is close enough to a just fifth to serve as a fifth, and some people are fond of it. | This '''limmic temperaments''' page collects various temperaments tempering out the Pythagorean limma, [[256/243]]. As a consequence, [[3/2]] is always represented by 3\5, 720 [[cent]]s assuming pure octaves. While quite sharp, this is close enough to a just fifth to serve as a fifth, and some people are fond of it. | ||
== | == Blackwood == | ||
Subgroup: 2.3.5 | Subgroup: 2.3.5 | ||
| Line 17: | Line 16: | ||
[[Badness]]: 0.063760 | [[Badness]]: 0.063760 | ||
== | == Blacksmith == | ||
[[File:blacksmith10.jpg|alt=blacksmith10.jpg|thumb|Lattice of blacksmith]] | [[File:blacksmith10.jpg|alt=blacksmith10.jpg|thumb|Lattice of blacksmith]] | ||
| Line 45: | Line 44: | ||
POTE generator: ~5/4 = 394.948 | POTE generator: ~5/4 = 394.948 | ||
Vals: {{Val list| 5, 10, 15, 40be, 55be, 70bde, 85bcde}} | Vals: {{Val list| 5, 10, 15, 40be, 55be, 70bde, 85bcde }} | ||
Badness: 0.024641 | Badness: 0.024641 | ||
| Line 58: | Line 57: | ||
POTE generator: ~5/4 = 391.037 | POTE generator: ~5/4 = 391.037 | ||
Vals: {{Val list| 5, 10, 15, 25e, 40bef}} | Vals: {{Val list| 5, 10, 15, 25e, 40bef }} | ||
Badness: 0.020498 | Badness: 0.020498 | ||
| Line 102: | Line 101: | ||
== Blackweed == | == Blackweed == | ||
Blackweed is so named because the | Blackweed is so named because the 20EDO tuning has 4\20 as the period and 420¢ as the generator. | ||
Subgroup: 2.3.14/11 | Subgroup: 2.3.14/11 | ||
Comma: 256/243 | |||
Mapping: [ | Mapping: [{{val|5 8 0}}, {{val|0 0 1}}] | ||
Mapping generators: ~9/8, ~14/11 | Mapping generators: ~9/8, ~14/11 | ||
| Line 114: | Line 113: | ||
POTE generator: ~14/11 = 413.7785 | POTE generator: ~14/11 = 413.7785 | ||
Vals: {{Val list|20, 35b }} | Vals: {{Val list| 20, 35b }} | ||
[[Category:Regular temperament theory]] | [[Category:Regular temperament theory]] | ||
Revision as of 02:05, 10 October 2021
This limmic temperaments page collects various temperaments tempering out the Pythagorean limma, 256/243. As a consequence, 3/2 is always represented by 3\5, 720 cents assuming pure octaves. While quite sharp, this is close enough to a just fifth to serve as a fifth, and some people are fond of it.
Blackwood
Subgroup: 2.3.5
Comma list: 256/243
Mapping: [⟨5 8 0], ⟨0 0 1]]
Mapping generators: ~9/8, ~5
POTE generator: ~5/4 = 399.594
Badness: 0.063760
Blacksmith
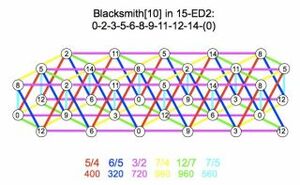
Subgroup: 2.3.5.7
Comma list: 28/27, 49/48
Mapping: [⟨5 8 0 14], ⟨0 0 1 0]]
Mapping generators: ~7/6, ~5
Wedgie: ⟨⟨ 0 5 0 8 0 -14 ]]
POTE generator: ~5/4 = 392.767
Badness: 0.025640
11-limit
Subgroup: 2.3.5.7.11
Comma list: 28/27, 49/48, 55/54
Mapping: [⟨5 8 0 14 29], ⟨0 0 1 0 -1]]
POTE generator: ~5/4 = 394.948
Vals: Template:Val list
Badness: 0.024641
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 28/27, 40/39, 49/48, 55/54
Mapping: [⟨5 8 0 14 29 7], ⟨0 0 1 0 -1 1]]
POTE generator: ~5/4 = 391.037
Vals: Template:Val list
Badness: 0.020498
Farrier
Subgroup: 2.3.5.7.11
Comma list: 28/27, 49/48, 77/75
Mapping: [⟨5 8 0 14 -6], ⟨0 0 1 0 2]]
POTE generator: ~5/4 = 398.070
Vals: Template:Val list
Badness: 0.029200
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 28/27, 40/39, 49/48, 66/65
Mapping: [⟨5 8 0 14 -6 7], ⟨0 0 1 0 2 1]]
POTE generator: ~5/4 = 396.812
Vals: Template:Val list
Badness: 0.022325
Ferrum
Subgroup: 2.3.5.7.11
Comma list: 28/27, 35/33, 49/48
Mapping: [⟨5 8 0 14 6], ⟨0 0 1 0 1]]
POTE generator: ~5/4 = 374.763
Vals: Template:Val list
Badness: 0.030883
Blackweed
Blackweed is so named because the 20EDO tuning has 4\20 as the period and 420¢ as the generator.
Subgroup: 2.3.14/11
Comma: 256/243
Mapping: [⟨5 8 0], ⟨0 0 1]]
Mapping generators: ~9/8, ~14/11
POTE generator: ~14/11 = 413.7785
Vals: Template:Val list