Exterior algebra: Difference between revisions
Redirected page to Dave Keenan & Douglas Blumeyer's guide to EA for RTT Tag: New redirect |
No edit summary |
||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Wikipedia}} | |||
'''Exterior algebra''' is a type of {{w|Algebra over a field|algebra}} which has a product, called '''exterior product''' or '''wedge product''' and denoted with <math>\wedge</math>, such that <math>v \wedge v = 0</math> for every vector <math>v</math> in the vector space <math>V</math>. | |||
In [[regular temperament theory]], exterior algebra is typically applied to the vector space of [[val]]s (or maps). The exterior product of two or more vals is called a multival, and its canonical form is called a [[wedgie]] (or [[Plücker coordinates]]), which can be used to uniquely identify a regular temperament. | |||
In many cases, the same things can be accomplished using matrix algebra or exterior algebra. The matrix approach is usually preferred for pedagogical reasons (more people are familiar with matrices compared to exterior products) and computational reasons, (most common numerical libraries are primarily intended for matrix operations). | |||
Still, in some more abstract or advanced applications, the exterior algebra may still be used if it is more natural. | |||
=== Wedge product === | |||
[[File:Wedgediagram .png|thumb|504x504px|Wedge product diagram]] | |||
The wedge product is the n-dimensional generalization of the cross product. It produces not a vector, but a structure called a ''multivector'' with entries corresponding to combinations of entries in the starting vectors. For two vectors of the same length, [a<sub>1</sub> a<sub>2</sub> a<sub>3</sub> ... a<sub>n</sub>] and [b<sub>1</sub> b<sub>2</sub> b<sub>3</sub> ... b<sub>n</sub>], we go through every pair of indices ''i, j'' up to ''n'' where ''j'' > ''i,'' and the entry c<sub>i,j</sub> of the wedge product is a<sub>i</sub>b<sub>j</sub> - b<sub>i</sub>a<sub>j</sub>. c<sub>j,i</sub> is equal to -(c<sub>i,j</sub>), and c<sub>i,i</sub> where the two indices are the same is 0. | |||
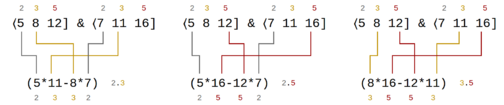
The wedge product is equivalent to [[map-merging]] or [[Edo join|edo joins]] in regular temperament theory (and can thus be written with the symbol &), and is used to combine [[vals]] into structures which represent higher-rank temperaments (called multivals or [[wedgies]]). For example, wedging ⟨5 8 12] and ⟨7 11 16] (the patent vals for 5edo and 7edo) yields ⟨⟨(5*11-8*7) (5*16-12*7) (8*16-12*11)]], which simplifies to ⟨⟨(55-56) (80-84) (128-132)]] and thus to ⟨⟨-1 -4 -4]], which is the wedgie for 5 & 7, a.k.a. meantone. | |||
The wedge product can be generalized to combine ''n'' vals together, where instead of every pair of indices, we have every combination of ''n'' indices. This results in wedgies for rank-3 temperaments and beyond. | |||
For a higher-dimensional multivector with elements c<sub>i, j, k...</sub>, the entries at all permutations of the same indices have the same absolute value, and swapping two indices flips the sign. | |||
== See also == | |||
* [[Wedgie]] | |||
* [[Hodge dual]] | |||
* [[Dave Keenan & Douglas Blumeyer's guide to EA for RTT]] | |||
* [[Interior product]] | |||
* [[Recoverability]] | |||
* [[User:Mike Battaglia/Exterior Norm Conjecture Table]] | |||
[[Category:Exterior algebra| ]] <!-- main article --> | |||
Latest revision as of 07:48, 21 August 2025
Exterior algebra is a type of algebra which has a product, called exterior product or wedge product and denoted with [math]\displaystyle{ \wedge }[/math], such that [math]\displaystyle{ v \wedge v = 0 }[/math] for every vector [math]\displaystyle{ v }[/math] in the vector space [math]\displaystyle{ V }[/math].
In regular temperament theory, exterior algebra is typically applied to the vector space of vals (or maps). The exterior product of two or more vals is called a multival, and its canonical form is called a wedgie (or Plücker coordinates), which can be used to uniquely identify a regular temperament.
In many cases, the same things can be accomplished using matrix algebra or exterior algebra. The matrix approach is usually preferred for pedagogical reasons (more people are familiar with matrices compared to exterior products) and computational reasons, (most common numerical libraries are primarily intended for matrix operations). Still, in some more abstract or advanced applications, the exterior algebra may still be used if it is more natural.
Wedge product
The wedge product is the n-dimensional generalization of the cross product. It produces not a vector, but a structure called a multivector with entries corresponding to combinations of entries in the starting vectors. For two vectors of the same length, [a1 a2 a3 ... an] and [b1 b2 b3 ... bn], we go through every pair of indices i, j up to n where j > i, and the entry ci,j of the wedge product is aibj - biaj. cj,i is equal to -(ci,j), and ci,i where the two indices are the same is 0.
The wedge product is equivalent to map-merging or edo joins in regular temperament theory (and can thus be written with the symbol &), and is used to combine vals into structures which represent higher-rank temperaments (called multivals or wedgies). For example, wedging ⟨5 8 12] and ⟨7 11 16] (the patent vals for 5edo and 7edo) yields ⟨⟨(5*11-8*7) (5*16-12*7) (8*16-12*11)]], which simplifies to ⟨⟨(55-56) (80-84) (128-132)]] and thus to ⟨⟨-1 -4 -4]], which is the wedgie for 5 & 7, a.k.a. meantone.
The wedge product can be generalized to combine n vals together, where instead of every pair of indices, we have every combination of n indices. This results in wedgies for rank-3 temperaments and beyond.
For a higher-dimensional multivector with elements ci, j, k..., the entries at all permutations of the same indices have the same absolute value, and swapping two indices flips the sign.
