|
|
| (234 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| A scale satisfies the '''generator-offset property''' (also '''GO''', '''alternating generator''' or '''AG''') if it satisfies the following properties: | | A scale satisfies the '''generator-offset property''' if it satisfies the following properties: |
| # The scale is generated by two chains of stacked copies of a ''generator''. | | # The scale is generated by two chains of stacked copies of an interval called the ''generator''. |
| # The two chains are separated by an ''offset'' (the difference between the first note of the second chain and the first note of the first chain). | | # The two chains are separated by a different interval called the ''offset'' (the difference between the first note of the second chain and the first note of the first chain). |
| # The lengths of the chains differ by at most one. (1-3 can be restated as: The scale can be built by stacking two alternating generators (called ''alternants''), which do not necessarily take up the same number of steps.) | | # The lengths of the chains differ by at most one. (1-3 can be restated as: The scale can be built by stacking two alternating generators (called ''alternants'') a<sub>1</sub> and a<sub>2</sub>. Note that a<sub>1</sub> does not need to [[subtend]], i.e. occur as, the same number of steps as a<sub>2</sub>.) |
| # The generator always occurs as the same number of steps. For example, the generator is never both a 2-step and a 3-step. | | # The generator always occurs as the same number of steps. For example, the generator is never both a 2-step and a 3-step. |
|
| |
|
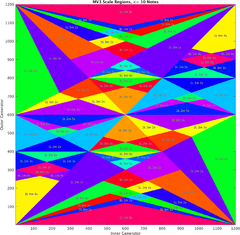
| [[File:MV3-Labeled.png|thumb|240px|Plot of at-most-decatonic MV3 GO scale regions in the plane.]] | | [[File:MV3-Labeled.png|thumb|240px|Plot of at-most-decatonic MV3 generator-offset scale regions in the plane.]] |
|
| |
|
| The [[Zarlino]] (3L 2M 2S) JI scale is an example of a GO scale, because it is built by stacking alternating 5/4 and 6/5 generators. The 7-limit version of [[diasem]] (5L 2M 2S) is another example, with generators 7/6 and 8/7. | | The [[Zarlino]] (3L 2M 2S) JI scale is an example of a generator-offset scale, because it is built by stacking alternating 5/4 and 6/5 generators. The 7-limit version of [[diasem]] (5L 2M 2S) is another example, with generators 7/6 and 8/7. |
|
| |
|
| More formally, a cyclic word ''S'' (representing the steps of a [[periodic scale]]) of size ''n'' is '''GO''' if it satisfies the following properties: | | Generator-offset scales generalize the notion of [[dipentatonic scale|dipentatonic]] and [[diheptatonic scale|diheptatonic]] scales where the pentatonic and heptatonic are [[MOS scales]]. A related but distinct notion is [[alternating generator sequence]]. While scales produced using the generator-offset procedure can be seen as a result of an alternating generator sequence of 2 alternants, the generator-offset perspective views the sum of the two alternants as the "canonical" generator, and the alternants as rather being possible choices of the offset which are effectively equivalent up to chirality. While a well-formed AGS scale requires each alternant in the AGS to subtend the same number of steps, the generator-offset property only requires each (aggregate) generator to subtend the same number of steps. |
| # ''S'' is generated by two chains of stacked generators g separated by a fixed offset δ; either both chains are of size ''n''/2, or one chain has size (''n'' + 1)/2 and the second has size (''n'' − 1)/2. Equivalently, ''S'' can be built by stacking a single chain of alternants g<sub>1</sub> and g<sub>2</sub>, resulting in a circle of the form either g<sub>1</sub> g<sub>2</sub> ... g<sub>1</sub> g<sub>2</sub> g<sub>1</sub> g<sub>3</sub> or g<sub>1</sub> g<sub>2</sub> ... g<sub>1</sub> g<sub>2</sub> g<sub>3</sub>. | | |
| | Note: In Inthar's contribution to [[aberrismic theory]], this term has been superseded by [[guide frame]]s. |
| | == Mathematical definition == |
| | More formally, a cyclic word ''S'' (representing the steps of a [[periodic scale]]) of size ''n'' is '''generator-offset''' if it satisfies the following properties: |
| | # ''S'' is generated by two chains of stacked generators g separated by a fixed offset δ; either both chains are of size ''n''/2 (implying ''n'' is even), or one chain has size (''n'' + 1)/2 and the second has size (''n'' − 1)/2 (implying ''n'' is odd). |
| # The scale is ''well-formed'' with respect to g, i.e. all occurrences of the generator g are ''k''-steps for a fixed ''k''. | | # The scale is ''well-formed'' with respect to g, i.e. all occurrences of the generator g are ''k''-steps for a fixed ''k''. |
|
| |
|
| This doesn't imply that g<sub>1</sub> and g<sub>2</sub> are the same number of scale steps. For example, 5-limit [[blackdye]] has g<sub>1</sub> = 9/5 (a 9-step) and g<sub>2</sub> = 5/3 (a 7-step).
| |
|
| |
| More generally, we say that a scale is ''m'''''-GO''' if both of the following hold:
| |
| # the scale consists of ''m'' + 1 chains of stacked generator g (implying ''m'' offsets δ<sub>1</sub>, ...,δ<sub>''m''</sub> from a fixed chain), each chain having either ''j'' or ''j'' + 1 notes.
| |
| # The scale is well-formed with respect to g.
| |
|
| |
| (Thus 1-GO is the same thing as GO.)
| |
|
| |
| An ''m''-GO scale can be interpreted as a scale in a rank-(''m'' + 2) [[regular temperament]], with basis p (period), g, δ<sub>1</sub>, ...,δ<sub>''m''</sub> (though the specific tuning used may be of lower rank).
| |
|
| |
| Note: On this page, non-italicized Latin variables refer to interval sizes, for example step sizes.
| |
| == Other definitions ==
| |
| * A strengthening of the generator-offset property, tentatively named the ''swung-generator-alternant property'' (SGA), states that the alternants g<sub>1</sub> and g<sub>2</sub> can be taken to always subtend the same number of scale steps, thus both representing "detemperings" of a generator of a single-period [[mos]] scale (otherwise known as a well-formed scale). All odd GO scales are SGA, and aside from odd GO scales, only xyxz satisfies this property. The Zarlino and diasem scales above are both SGA. [[Blackdye]] is GO but not SGA.
| |
|
| |
| == Theorems ==
| |
| === Proposition 1 (Properties of SGA scales) ===
| |
| Let ''S'' be a 3-step-size scale word in L, M, and s of length ''n'', and suppose ''S'' is SGA. Then:
| |
| # If ''n'' is odd, ''S'' is abstractly SV3 (i.e. SV3 for almost all tunings).
| |
| # ''S'' is of the form ''a''x ''b''y ''b''z for some permutation (x, y, z) of (L, M, s).
| |
| # The length of ''S'' is odd, or ''S'' is equivalent to xyxz.
| |
| # If ''n'' is odd, ''S'' = ''a''X ''b''Y ''b''Z is obtained from some mode of the (single-period) mos ''a''X 2''b''W by replacing all the W's successively with alternating Y's and Z's (or alternating Z's and Y's for the other chirality, fixing the mode of ''a''X 2''b''W). The two alternants differ by replacing one Y with a Z.
| |
| # ''S'' is pairwise-mos. That is, the following operations each result in a mos: setting L = M, setting L = s, and setting M = s.
| |
| # ''S'' is elimination-mos. That is, "tempering out" any one step size results in a mos.
| |
|
| |
| In particular, odd GO scales always satisfy these properties (see Proposition 2 below).
| |
|
| |
| [Note: This is not true with SGA replaced with GO; [[blackdye]] is a counterexample that is MV4.]
| |
| ==== Proof ====
| |
| Assuming SGA, we have two chains of generator g<sub>0</sub> (going right). The two cases are:
| |
| CASE 1: EVEN LENGTH
| |
| O-O-...-O (n/2 notes)
| |
| O-O-...-O (n/2 notes)
| |
| and
| |
| CASE 2: ODD LENGTH
| |
| O-O-O-...-O ((n+1)/2 notes)
| |
| O-O-...-O ((n-1)/2 notes).
| |
|
| |
| Label the notes (1, ''j'') and (2, ''j''), 1 ≤ ''j'' ≤ (number of notes in the chain), for notes in the upper and lower chain respectively.
| |
|
| |
| In case 1, let g<sub>1</sub> = (2, 1) − (1, 1) and g<sub>2</sub> = (1, 2) − (2, 1). We have the chain g<sub>1</sub> g<sub>2</sub> g<sub>1</sub> g<sub>2</sub> ... g<sub>1</sub> g<sub>3</sub>.
| |
|
| |
| Let ''r'' be odd and ''r'' ≥ 3. Consider the following abstract sizes for the interval class (''k''-steps) reached by stacking ''r'' generators:
| |
| # from g<sub>1</sub> ... g<sub>1</sub>, we get a<sub>1</sub> = (''r'' − 1)/2*g<sub>0</sub> + g<sub>1</sub> = (''r'' + 1)/2 g<sub>1</sub> + (''r'' − 1)/2 g<sub>2</sub>
| |
| # from g<sub>2</sub> ... g<sub>2</sub>, we get a<sub>2</sub> = (''r'' − 1)/2*g<sub>0</sub> + g<sub>2</sub> = (''r'' − 1)/2 g<sub>1</sub> + (''r'' + 1)/2 g<sub>2</sub>
| |
| # from g<sub>2</sub> (...even # of gens...) g<sub>1</sub> g<sub>3</sub> g<sub>1</sub> (...even # of gens...) g<sub>2</sub>, we get a<sub>3</sub> = (''r'' − 1)/2 g<sub>1</sub> + (''r'' − 1)/2 g<sub>2</sub> + g<sub>3</sub>
| |
| # from g<sub>1</sub> (...odd # of gens...) g<sub>1</sub> g<sub>3</sub> g<sub>1</sub> (...odd # of gens...) g<sub>1</sub>, we get a<sub>4</sub> = (''r'' + 1)/2 g<sub>1</sub> + (''r'' − 3)/2 g<sub>2</sub> + g<sub>3</sub>.
| |
|
| |
| Choose a tuning where g<sub>1</sub> and g<sub>2</sub> are both very close to but not exactly 1/2*g<sub>0</sub>, resulting in a scale very close to the mos generated by 1/2*g<sub>0</sub>. (i.e. g<sub>1</sub> and g<sub>2</sub> differ from 1/2*g<sub>0</sub> by ε, a quantity much smaller than the chroma of the ''n''/2-note mos generated by g<sub>0</sub>, which is |g<sub>3</sub> − g<sub>2</sub>|). Thus we have 4 distinct sizes for ''k''-steps:
| |
| # a<sub>1</sub>, a<sub>2</sub> and a<sub>3</sub> are clearly distinct.
| |
| # a<sub>4</sub> − a<sub>3</sub> = g<sub>1</sub> − g<sub>2</sub> ≠ 0, since the scale is a non-degenerate GO scale.
| |
| # a<sub>4</sub> − a<sub>1</sub> = g<sub>3</sub> − g<sub>2</sub> = (g<sub>3</sub> + g<sub>1</sub>) − (g<sub>2</sub> + g<sub>1</sub>) ≠ 0. This is exactly the chroma of the mos generated by g<sub>0</sub>.
| |
| # a<sub>4</sub> − a<sub>2</sub> = g<sub>1</sub> − 2 g<sub>2</sub> + g<sub>3</sub> = (g<sub>3</sub> − g<sub>2</sub>) + (g<sub>1</sub> − g<sub>2</sub>) = (chroma ± ε) ≠ 0 by choice of tuning.
| |
|
| |
| By applying this argument to 1-steps, we see that there must be 4 step sizes in some tuning, a contradiction. Thus g<sub>1</sub> and g<sub>2</sub> must themselves be step sizes. Thus we see that an even-length, unconditionally SV3, GO scale must be of the form xy...xyxz. But this pattern is not abstractly SV3 if ''n'' ≥ 6, since 3-steps come in 4 sizes: xyx, yxy, yxz and xzx. Thus ''n'' = 4 and the scale is xyxz. (Note that xyxz is not SV3, since it has only two kinds of 2-steps, xy and xz.) This proves (3).
| |
|
| |
| In case 2, let (2, 1) − (1, 1) = g<sub>1</sub>, (1, 2) − (2, 1) = g<sub>2</sub> be the two alternants. Let g<sub>3</sub> be the leftover generator after stacking alternating g<sub>1</sub> and g<sub>2</sub>. Then the generator circle looks like g<sub>1</sub> g<sub>2</sub> g<sub>1</sub> g<sub>2</sub> ... g<sub>1</sub> g<sub>2</sub> g<sub>3</sub>. Then the combinations of alternants corresponding to a step come in exactly 3 sizes:
| |
| # ''k''g<sub>1</sub> + (''k'' − 1)g<sub>2</sub>
| |
| # (''k'' − 1)g<sub>1</sub> + ''k''g<sub>2</sub>
| |
| # (''k'' − 1)g<sub>1</sub> + (''k'' − 1) g<sub>2</sub> + g<sub>3</sub>,
| |
| if a step is an odd number of generators (since the scale size is odd, we can always ensure this by taking octave complements of all the generators). The first two sizes must occur the same number of times. This proves (2).
| |
|
| |
| (The above holds for any odd ''n'' ≥ 3.)
| |
|
| |
| For (1), we now only need to see that if ''S'' has an odd number of notes and is SGA, ''S'' is abstractly SV3. But the argument in case 2 above works when you substitute any interval class in ''S'' instead of a 1-step (abstract SV3 wasn't used), hence any interval class comes in (abstractly) exactly 3 sizes.
| |
|
| |
| For (4), assume ''S'' is ''a''X ''b''Y ''b''Z, a odd. If ''b'' = 1, there's nothing to prove. So assume ''b'' > 1. Suppose for the sake of contradiction that Y′s and Z′s don't alternate perfectly. Assume that the perfect generator of ''a''X 2''b''W is ''i''X + ''j''W with ''j'' ≥ 2. (If ''j'' = 1, we can invert the generator to make ''j'' ≥ 2, since ''b'' > 1.)
| |
|
| |
| In ''S'', (''i'' + ''j'')-steps (representing the generator) are always one of the following:
| |
| # (a) the preimage of the perfect generator with the maximum number of Y's (at least 2 more than the # of Z's)
| |
| # (b) the preimage of the perfect generator with the maximum number of Z's (at least 2 more than the # of Y's)
| |
| # (c) the preimage of the perfect generator with an intermediate number of Y's and Z's between (a) and (b)
| |
| # (d) (the preimage of) the imperfect generator, having a different number of X's than (a), (b), and (c).
| |
| Since ''a'' + 2''b'' ≥ 5, there are at least 4 perfect generators, so there must be at least one of each of (a), (b), and (c), giving a contradiction to SV3. [Whenever the root of the (''i'' + ''j'')-step are moved within ''S'', the numbers of Y's and Z's change one at a time and reach a maximum at some choice of the root and a minimum with another choice, guaranteeing that intermediate values are reached. We can use this "intermediate value theorem" argument because (d) occurs at only one note.]
| |
|
| |
| Any generator of ''a''X 2''b''W must have an odd number of W steps (Otherwise, intervals with an odd number of W steps can't be generated.). We have finished proving (4).
| |
|
| |
| For (5), odd-numbered SGA scales are [[Fokker block]]s (in the 2-dimensional lattice generated by the generator and the offset). To see this, consider the following lattice depiction of such a scale:
| |
| x x x ... x
| |
| x x x ... x x
| |
| and use the vectors (-1, 2) and (ceil(n/2), 1) as the Fokker block chromas. A Fokker block has the property that tempering out by each of the chromas gives two mosses. These correspond to two of the temperings X = Y, Y = Z and X = Z. The third tempering follows by symmetry (by taking the other chirality).
| |
|
| |
| For (6), consider the mos ''a''X 2''b''W as chunks of X separated by W (tempering Y and Z together into W). Eliminating every other W turns it into a mos, because the sum of sizes of consecutive chunks of X (1st chunk with 2nd chunk, 3rd with 4th, ...) must form a mos. This is because the chunk sizes of X form a mos, and taking every ''k''th note of an ''n''-note mos where ''k'' divides ''n'' yields a mos. Since the result of setting X = 0 is the mos ''b''Y ''b''Z, ''S'' is elimination-mos.
| |
|
| |
| === Proposition 2 (Odd GO scales are SGA) ===
| |
| Suppose that a periodic scale satisfies the following:
| |
| * is generator-offset
| |
| * has odd size ''n''.
| |
|
| |
| Then the scale is SGA.
| |
|
| |
| ==== Proof ====
| |
| Assume that the generator is a ''k''-step and ''k'' is even. (If ''k'' is not even, invert the generator.) On some tonic ''p'' we have a chain of ceil(''n''/2) notes and on some other note ''p′'' = ''p'' + offset (not on the first chain) we'll have floor(''n''/2) notes.
| |
|
| |
| We must have gcd(''k'', ''n'') = 1. If not, since ''n'' is odd, gcd(''k'', ''n'') is an odd number at least 3, and the ''k''-steps must form more than 2 parallel chains.
| |
|
| |
| By modular arithmetic we have ''rk'' mod ''n'' = ''k''/2 iff ''r'' = ceil(''n''/2) mod ''n''. (Since gcd(2, ''n'') = 1, 2 is multiplicatively invertible mod ''n'', and we can multiply both sides by 2 to check this.) This proves that the offset, which must be reached after ceil(''n''/2) generator steps, is a ''k''/2-step, as desired. (If the offset wasn't reached in ceil(''n''/2) steps, the two generator chains either wouldn't be disjoint or wouldn't have the assumed lengths.)
| |
|
| |
| === Proposition 3 (Properties of even GO scales) ===
| |
| GO scales of even size have the following properties:
| |
| # They are two parallel mosses of size ''n''/2 generated by g, with offset a ''k''-step with ''k'' odd
| |
| # They are ''not'' SV3
| |
| # They are ''not'' chiral
| |
| ==== Proof ====
| |
| (1) and (2) were proved in the proof of Prop 1. (3) is easy to check using (1).
| |
|
| |
| === Theorem 4 (PWF implies SV3 and either GO or abacaba) ===
| |
| Let ''S''(a, b, c) be a scale word in three '''Z'''-linearly independent step sizes a, b, c. Suppose ''S'' is PWF. Then ''S'' is SV3 and has an odd number of notes. Moreover, ''S'' is either GO or equivalent to the scale word abacaba.
| |
| ==== Proof ====
| |
| ===== If the generator of a projection of ''S'' is a ''k''-step, the word of stacked ''k''-steps in ''S'' is PWF =====
| |
| Suppose ''S'' has ''n'' notes (after dealing with small cases, we may assume ''n'' ≥ 7) and ''S'' projects to single-period mosses ''S''<sub>1</sub> (via identifying b with c), ''S''<sub>2</sub> (via identifying a with c) and ''S''<sub>3</sub> (via identifying a with b). Suppose ''S''<sub>1</sub>'s generator is a ''k''-step, which comes in two sizes: P, the perfect ''k''-step, and I, the imperfect ''k''-step. By stacking ''k''-steps, we get two words of length ''n'' of ''k''-steps of ''S''<sub>2</sub> and ''S''<sub>3</sub>, respectively. These two-"step-size" words, which we call Σ<sub>2</sub> and Σ<sub>3</sub>, must be mosses, since ''m''-steps in the new words correspond to ''mk''-steps in the mos words ''S''<sub>1</sub> and ''S''<sub>2</sub>, which come in at most two sizes. Since ''S''<sub>1</sub> is a single-period mos, gcd(''k'', ''n'') = 1. Hence when 0 < ''m'' < ''n'', ''mk'' is ''not'' divisible by ''n'' and ''mk''-steps come in ''exactly'' two sizes; hence both Σ<sub>2</sub> and Σ<sub>3</sub> are single-period mosses.
| |
|
| |
| index: 1 2 3 4 ... ''n''
| |
| Σ<sub>1</sub>: P P P P ... P I
| |
| Σ<sub>2</sub>: [some mos]
| |
| Σ<sub>3</sub>: [some mos]
| |
|
| |
| ===== Two sizes of ''k''-steps in ''S'' project to ''S''<sub>1</sub>'s perfect generator =====
| |
| We can write sizes of intervals in ''S'' as vectors (''p'', ''q'', ''r'') using the basis (a, b, c).
| |
|
| |
| Suppose for sake of contradiction that only one size of ''k''-step (α, β, γ) in ''S'' projects to P in ''S''<sub>1</sub>. Then projecting to ''S''<sub>2</sub> shows that ''S''<sub>2</sub>'s generator is the ''k''-step (α + γ)*(a~c) + βb, and Σ<sub>2</sub>'s imperfect generator is located at index ''n'', like Σ<sub>1</sub>'s imperfect generator is. Then ''S''<sub>1</sub> and ''S''<sub>2</sub> are the same mode of the same mos pattern (up to knowing which step size is the bigger one). Assume the L of ''S''<sub>1</sub> (it could be s, but it doesn't matter) is the result of identifying b and c, and all instances of s in ''S''<sub>1</sub> come from a. Then the steps of ''S''<sub>2</sub> corresponding to the L of ''S''<sub>1</sub> must be either all b's or all a~c's, thus these steps are all b's in ''S'' (otherwise they would be identified with the a, against the assumption that ''S''<sub>1</sub> and ''S''<sub>2</sub> are the same mos pattern and mode). So ''S'' has only two step sizes (a and b), contradicting the assumption that ''S'' has exactly three step sizes.
| |
|
| |
| Only two sizes of ''k''-steps of ''S'' can project to P in ''S''<sub>1</sub>, for if there are three sizes of ''k''-steps (α, β, γ), (α, β′, γ′), (α, β′′, γ′′) in ''S'' that project to P, then β, β′ and β′′ are three distinct values. Thus these would project to three different ''k''-steps in ''S''<sub>3</sub>, contradicting the mos property of ''S''<sub>3</sub>.
| |
|
| |
| ===== Some implications of the above =====
| |
| Suppose Q = (α, β, γ) ≠ R = (α, β′, γ′) are the two ''k''-steps in ''S'' that project to P. Then T = (α′, β′′, γ′′) projects to I. Here the values in each component differ by at most 1, and α ≠ α′. Then the cyclic word Λ<sub>1</sub> formed by the a-components of the ''k''-steps in P is α...αα′. Since Σ<sub>2</sub> is a single-period mos pattern of βb + (''n'' − β)(a~c) and β′a + (''n'' − β′)(a~c), the cyclic word Λ<sub>2</sub> = the pattern of β and β′ must be a single-period mos. Similarly, Λ<sub>3</sub> = the pattern of γ and γ′ is a single-period mos.
| |
|
| |
| Suppose Λ<sub>2</sub> is the mos λβ μβ′. Then Λ<sub>3</sub> is the mos (λ ± 1)γ (μ ∓ 1)γ′. Since neither Λ<sub>2</sub> nor Λ<sub>3</sub> are multimosses, and at least one of μ and (μ ∓ 1) are even, it is now immediate that ''n'' is odd.
| |
|
| |
| Either β′′ = β or β′′ = β′. Assume β′′ = β′. Then γ′′ = γ, and Λ<sub>3</sub> is (λ + 1)γ (μ − 1)γ′. Also assume that the first ''k''-step in Σ is Q. Then we have:
| |
| 1 … ''n''
| |
| Σ = Q ''W''(Q, R) T
| |
| Λ<sub>1</sub> = α … α α′
| |
| Λ<sub>2</sub> = β ''W''(β, β′) β′
| |
| Λ<sub>3</sub> = γ ''W''(γ, γ′) γ
| |
| where ''W'' = ''W''(''x'', ''y'') is a word in two variables ''x'' and ''y'', of length ''n'' − 2.
| |
|
| |
| ===== Case analysis =====
| |
| Since, by our assumption, Λ<sub>3</sub> has two γs in a row, Λ<sub>3</sub> must have more γ than γ′, so μ − 1 < ''n''/2. Since Λ<sub>3</sub> is a mos, μ − 1 ≥ 1. So we have 2 ≤ μ ≤ ceil(''n''/2).
| |
|
| |
| We have three cases to consider:
| |
|
| |
| '''Case 1''': μ = 2, i.e. Λ<sub>2</sub> is the mos (''n'' − 2)β 2β′.
| |
|
| |
| For Λ<sub>2</sub> to be a mos, the first, and only, occurrence of R must be at either ''f'' = floor(''n''/2) or ceil(''n''/2). We may assume that it is at ''f''; otherwise flip the chain and reindex the words to start at 2''f''.
| |
|
| |
| 1 … ''f'' … 2''f'' ''n''
| |
| Σ = Q … Q R Q … Q T
| |
| Λ<sub>1</sub> = α … α α α … α α′
| |
| Λ<sub>2</sub> = β … β β′ β … β β′
| |
| Λ<sub>3</sub> = γ … γ γ′ γ … γ γ
| |
|
| |
| We need only consider stacks up to ''f''-many ''k''-steps. Either:
| |
| # the stack has only copies of Q and R; or
| |
| # the stack has one T and does not contain any R (since it's more than ''f'' − 1 generators away).
| |
| These give exactly three distinct sizes for every interval class. Hence ''S'' is SV3.
| |
|
| |
| In this case S has two chains of Q, one with floor(''n''/2) notes and and one with ceil(''n''/2) notes. Every instance of Q must be a ''k''-step, since by '''Z'''-linear independence Q = αa + βb + γc is the only way to write Q in the basis (a, b, c); so ''S'' is well-formed with respect to Q. Thus ''S'' also satisfies the generator-offset property with generator Q.
| |
|
| |
| '''Case 2:''' μ ≥ ceil(''n''/2), i.e. Λ<sub>2</sub> has fewer β than β′.
| |
|
| |
| Since Λ<sub>3</sub> has more β than β′, Λ<sub>2</sub> is floor(''n''/2)β ceil(''n''/2)β′, and Λ<sub>3</sub> is ceil(''n''/2)γ floor(''n''/2)γ′. There is a unique mode of ceil(''n''/2)γ floor(''n''/2)γ′ that both begins and ends with γ, namely γγ′γγ′…γγ′γ. Thus Λ<sub>2</sub> is ββ′ββ′…ββ′β′. It is now easy to see that if the number of ''k''-steps stacked is odd, then there are two sizes that do not contain T and one size that contains T; if the number of ''k''-steps stacked is even, then there is one size that does not contain T and two sizes that contain T. Hence ''S'' is SV3.
| |
|
| |
| In this case we have Σ = QRQR…QRT, and ''S'' is well-formed with respect to the generator Q + R, thus ''S'' satisfies the generator-offset property.
| |
|
| |
| '''Case 3:''' 3 ≤ μ ≤ floor(''n''/2).
| |
|
| |
| Λ<sub>2</sub> has a chunk of βs (after the first β′) of size ''x'' = either floor(''n''/μ) (≥ floor(''n''/floor(''n''/2)) = 2) or ceil(''n''/μ) (= floor(''n''/μ) + 1). Hence Λ<sub>3</sub> has a chunk of γs of that same size. Λ<sub>3</sub> also has a chunk that crosses index ''n'', which must be of size ''y'' = at least 2*(floor(''n''/μ) − 1) + 1 (Λ<sub>3</sub> might have chunks of size floor(''n''/μ) − 1 and floor(''n''/μ) instead) = 2*floor(''n''/μ) − 1, and at most 2*(floor(''n''/μ) + 1) + 1 = 2*floor(''n''/μ) + 3 (if Λ<sub>3</sub> has chunks of size floor(''n''/μ) and ceil(''n''/μ)). The difference between the chunk sizes is ''y'' − ''x'', which must be 0 or 1, since Λ<sub>3</sub> is a mos. We thus have the following subcases: (In the following, chunk of Λ<sub>2</sub> means chunk of β, and chunk of Λ<sub>3</sub> means chunk of γ.)
| |
|
| |
| '''Case 3.1:''' (''x'', ''y'') = (floor(''n''/μ), 2*floor(''n''/μ) − 1).
| |
|
| |
| Since ''y'' − ''x'' = floor(''n''/μ) − 1 and floor(''n''/μ) ≥ 2, we have: ''x'' = floor(''n''/μ) = 2 and ''y'' − ''x'' = 1; hence ''y'' = 2*floor(''n''/μ) − 1 = 3. The chunk in Λ<sub>3</sub> whose size is 3 is made from two chunks in Λ<sub>2</sub> of size 1. (So Λ<sub>2</sub> has chunks of size 1 and 2, and Λ<sub>3</sub> has chunks of size 2 and 3.)
| |
|
| |
| Λ<sub>2</sub> has two consecutive chunks of size 1. Since chunk sizes form a mos, Λ<sub>2</sub> has more chunks of size 1 than it has chunks of size 2.
| |
|
| |
| Use ''w''[''i'' : ''j''] to denote the slice of the cyclic word ''w'' that includes both endpoints, i.e. the word ''w''[''i''] ''w''[''i'' + 1] ... ''w''[''j''] where indices are taken to be elements of '''Z'''/''n'''''Z'''. Λ<sub>2</sub> has only two chunks of size 1, Λ<sub>2</sub>[(''n'' − 1) : (''n'' − 1)] and Λ<sub>2</sub>[1 : 1], since otherwise Λ<sub>3</sub> would have a chunk of size 1 within Λ<sub>3</sub>[1 : (''n'' − 1)]. Thus Λ<sub>2</sub> has exactly one chunk of size 2. Thus Λ<sub>2</sub> = ββ′βββ′ββ′ and Λ<sub>3</sub> = γγ′γγγ′γγ. Thus we have:
| |
|
| |
| 1 2 3 4 5 6 7
| |
| Σ = Q R Q Q R Q T
| |
| Λ<sub>1</sub> = α α α α α α α′
| |
| Λ<sub>2</sub> = β β′ β β β′ β β′
| |
| Λ<sub>3</sub> = γ γ′ γ γ γ′ γ γ
| |
|
| |
| Suppose a step of ''S'' is reached by stacking ''t''-many ''k''-steps. We have three cases after accounting for equave complements:
| |
|
| |
| # ''t'' = 1: ''S'' is equivalent to abacaba.
| |
| # ''t'' = 2: ''S'' is QR QQ RQ TQ RQ QR QT => ''S'' is equivalent to abacaba.
| |
| # ''t'' = 3: ''S'' is QRQ QRQ TQR QQR QTQ RQQ RQT => ''S'' is equivalent to abacaba.
| |
|
| |
| (This also implies ''S'' is SV3.)
| |
|
| |
| '''Case 3.2''': (''x'', ''y'') = (floor(''n''/μ) + 1, 2*floor(''n''/μ) − 1) is impossible because ''y'' = 2*floor(''n''/μ) − 1 can only occur if Λ<sub>3</sub> has chunks of size floor(''n''/μ) − 1 and floor(''n''/μ), which contradicts the size of ''x''.
| |
|
| |
| '''Case 3.3''': (''x'', ''y'') = (floor(''n''/μ) + 1, 2*floor(''n''/μ)) is similarly impossible; ''y'' = 2*floor(''n''/μ) can only occur if Λ<sub>3</sub> has chunks of size floor(''n''/μ) − 1 and floor(''n''/μ), which contradicts the size of ''x''.
| |
|
| |
| The remaining cases are all impossible because they imply ''y'' − ''x'' ≥ 2:
| |
|
| |
| * '''Case 3.4''': (''x'', ''y'') = (floor(''n''/μ) + 1, 2*floor(''n''/μ) + 1)
| |
| * '''Case 3.5''': (''x'', ''y'') = (floor(''n''/μ) + 1, 2*floor(''n''/μ) + 2)
| |
| * '''Case 3.6''': (''x'', ''y'') = (floor(''n''/μ) + 1, 2*floor(''n''/μ) + 3)
| |
| * '''Case 3.7''': (''x'', ''y'') = (floor(''n''/μ), 2*floor(''n''/μ))
| |
| * '''Case 3.8''': (''x'', ''y'') = (floor(''n''/μ), 2*floor(''n''/μ) + 1)
| |
| * '''Case 3.9''': (''x'', ''y'') = (floor(''n''/μ), 2*floor(''n''/μ) + 2)
| |
| * '''Case 3.10''': (''x'', ''y'') = (floor(''n''/μ), 2*floor(''n''/μ) + 3)
| |
|
| |
| == Open conjectures ==
| |
| === Conjecture ("SV3 Structure Theorem") ===
| |
| ==== Conjecture 1 ====
| |
| If a 3-step size scale word that is ''a''x ''b''y ''c''z is
| |
| # abstractly SV3 (strict variety 3, i.e. every ''k''-step except multiples of the equave comes in ''exactly'' 3 sizes, for almost all tunings),
| |
| # has ''odd'' length,
| |
| # has gcd(''a'', ''b'', ''c'') = 1,
| |
| # is not of the form xyzyx or xyxzxyx,
| |
| then it is GO (and therefore SGA). (a converse to Proposition 1)
| |
|
| |
| By Theorem 4, this conjecture would follow from proving that such scales are PWF.
| |
|
| |
| ==== Conjecture 2 ====
| |
| If a 3-step size scale word that is ''a''x ''b''y ''c''z is abstractly SV3, then two of ''a'', ''b'', ''c'' are equal.
| |
|
| |
| === Conjecture ("MV3 Sequences") ===
| |
| Given any two generators, we can iterate them to any number of notes and see what the maximum-variety of the resulting scale is. In particular, we can look at those scale sizes which are MV3, and thus compute the '''MV3 sequence''' for the pair of generators (similar to the "MOS sequence" one can compute for one generator). Thus, for any pair of generators, we can form the associated sequence of increasingly large MV3 scales.
| |
|
| |
| Surprisingly, for almost all pairs of generators, this sequence seems to terminate after some (usually relatively small) scale. That is, if we simply take all possible pairs of generators between 0 and 1200 cents, and for each pair we compute the MV3 sequence for all generator pairs up to some maximum ''N'', such as 1000, we can easily see that most points will have only a few entries in it, after which no MV3 scales are apparently generated. It would seem to be true that as the two generators get closer and closer in size, the MV3 sequence gets longer and longer, until when the two generators are equal you have an infinite-length sequence (corresponding to MOS).
| |
|
| |
| It is pretty easy to see this behavior is true if we simply compute the MV3 sequences up to any very large ''N'', far beyond the scale sizes we typically use in music theory, but it would be good to have a proof.
| |
|
| |
| == Open questions ==
| |
| This heading has those open questions for which no conjecture has yet been formed either way. (These can be updated as necessary)
| |
|
| |
| # Given any arbitrary MOS (or DE, etc) scale with at least three notes per period, is there *always* a MV3 GO scale which can be derived as a "detempering" of that scale? Or is this only true for some MOS's? For instance, the MOS LLsLLLs has the MV3 GO scale LmsLmLs as a detempering. Does a similar MV3 detempering exist for every possible DE scale with at least three notes per period, or at least for strict MOS's with one period per octave (e.g. well-formed scales)?
| |
| # The scale tree is a great way to analyze MOS scales. For any generator, we can compute the various MOS's it forms if we simply look at the scale tree, and indeed MOS "words" like LLsLLLs can be identified with regions on the scale tree (in this situation the interval between 4/7 and 3/5). A similar "scale plane" should exist for GO-MV3 scales, where given some word representing a GO-MV3 scale, we can look at the set of points on the generator plane which generates it; these seem to often be triangles, with the lines corresponding to MOS's and the vertices corresponding to EDOs (though is this always true?). What is the big picture of this scale plane? Can we use Viggo Brun's algorithm for this, generalizing the theory of continued fractions? Is there some simple formula we can use to predict, given some GO-MV3 scale, which region on the scale plane it corresponds to? Can we plot simple generator-size-proportions as points in this space? And so on.
| |
| # In the theory of MOS, there is a second [[MOS Scale Family Tree|scale tree]] that is less frequently talked about, which Erv Wilson calls the "Rabbit Sequence" ([http://www.anaphoria.com/RabbitSequence.pdf Erv Wilson's original version], [https://mikebattagliamusic.com/MOSTree/MOSTreeab.html interactive version 1], [https://mikebattagliamusic.com/MOSTree/MOSTreeLs.html interactive version 2]). This is a tree for which each MOS word has two children, depending on if the MOS is "soft" (with L/s < 2) or "hard" (with L/s > 2). For instance, LsLss has the two children LLsLLLs and ssLsssL. Does a similar scale plane exist for these GO-MV3 scales?
| |
|
| |
| == Falsified conjectures ==
| |
| === All mosses have an MV3 detempering (Counterexample: LsLsLsLsLs) ===
| |
| LsLsLsLsLs does ''not'' have an MV3 detempering: Wolog we “detemper” L to L and M.
| |
|
| |
| LsMsLsMsLs is not MV3: LsM LsL sMs sLs
| |
|
| |
| LsMsLsMsMs can be rotated to MsLsMsLsMs which is not MV3 by symmetry with LsMsLsMsLs.
| |
|
| |
| LsMsMsMsMs is not MV3: LsM MLM sMs sLs
| |
|
| |
| MsLsLsLsLs not MV3 for the same reason as LsMsMsMsMs
| |
|
| |
|
| [[Category:GO scales| ]]<!--Main article-->
| |
| [[Category:Scale]] | | [[Category:Scale]] |