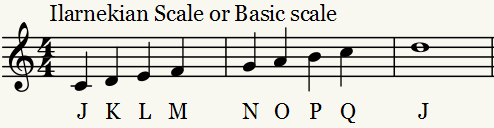13edo, the edo for 2.5.9.11.13.17.19.21

13edo: 13 equal divisions of the octave

13edo refers to a tuning system which divides the octave (frequency ratio 2:1) into 13 equal parts. It is the sixth prime edo, following 11edo and coming before 17edo. The steps less than 600¢ are narrower than their nearest 12edo approximation, while those greater than 600¢ are wider. This allows for some neat ear-bending tricks, whereby melodic gestures reminiscent of 12edo can quickly arrive at an unfamiliar place.

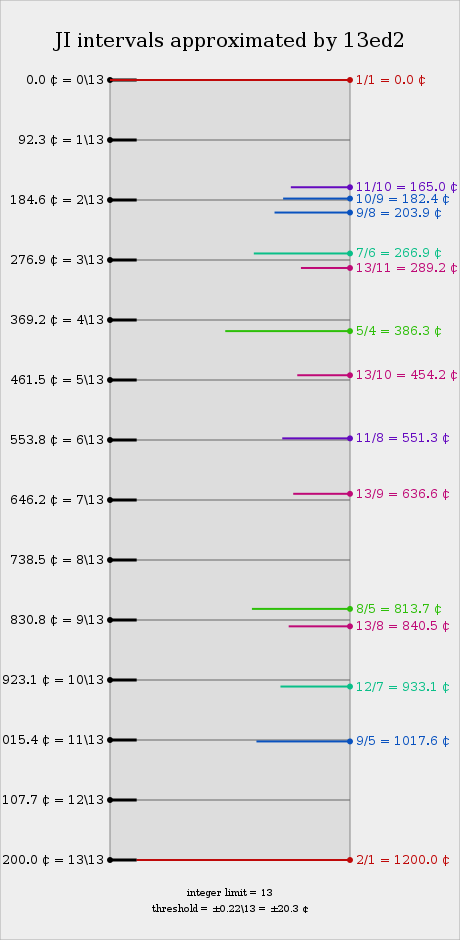
As a temperament of 21-odd-limit Just Intonation, 13edo has excellent approximations to the 11th and 21st harmonics, and reasonable approximations to the 5th, 9th, 13th, 17th, and 19th harmonics. For most purposes it does not offer acceptable approximations to the 3rd, 7th, or 15th. The lack of reasonable approximation to the 3rd harmonic makes 13edo unsuitable for common-practice music, but its good approximations to ratios of 11, 13, and 21 make it a very xenharmonic tuning, as these identities are not remotely represented in 12edo. Despite its reputation for dissonance, it is an excellent rank-1 temperament on the 2.5.9.11.13.17.19.21 subgroup, and has a substantial repertoire of complex consonances for its small size.

Degree	Cents	Approximated 21-limit Ratios*	Erv Wilson	Archaeotonic	Oneirotonic	26edo names	Kentaku
0	0.00	1/1	H	C	C	C	J
1	92.31	17/16, 18/17, 19/18, 20/19, 21/20, 22/21	β	C#/Db	C#/Db	Cx/Dbb	J#/Kb
2	184.62	9/8, 10/9, 11/10, 19/17, 21/19	A	D	D	D	K
3	276.92	7/6, 13/11, 20/17, 19/16, 22/19	δ	D#/Eb	D#/Eb	Dx/Ebb	K#/Lb
4	369.23	5/4, 11/9, 16/13, 26/21	C	E	E	E	L
5	461.54	13/10, 17/13, 21/16, 22/17	B	E#/Fb	F	Ex/Fb	M
6	553.85	11/8, 18/13, 26/19	ε	F	F#/Gb	F#	M#/Nb
7	646.15	16/11, 13/9, 19/13	D	F#/Gb	G	Gb	N
8	738.46	17/11, 20/13, 26/17, 32/21	γ	G	G#/Hb	G#	N#/Ob
9	830.77	8/5, 13/8, 18/11, 21/13	F	G#/Ab	H	Ab	O
10	923.08	17/10, 12/7, 22/13, 19/11	E	A	A	A#	P
11	1015.38	9/5, 16/9, 20/11, 34/19, 38/21	α	A#/Bb	A#/Bb	Bb	P#/Qb
12	1107.69	17/9, 19/10, 21/11, 32/17, 36/19, 40/21	G	B/Cb	B	B#/Cbb	Q
13	1200.00	2/1	H	C/B#	C	C	J

based on treating 13-EDO as a 2.5.9.11.13.21 subgroup temperament; other approaches are possible.

13edo can also be notated with ups and downs. The notational 5th is the 2nd-best approximation of 3/2, 7\13. This is 56¢ flat of 3/2, and the best approximation is 36¢ sharp, noticeably better. But using the 2nd-best 5th allows conventional notation to be used, including the staff, note names, relative notation, etc. There are two ways to do this. The first way preserves the melodic meaning of sharp/flat, major/minor and aug/dim, in that sharp is higher pitched than flat, and major/aug is wider than minor/dim. The disadvantage to this approach is that conventional interval arithmetic no longer works. e.g. M2 + M2 isn't M3, and D + M2 isn't E. Chord names are different because C - E - G isn't P1 - M3 - P5.

The second approach preserves the harmonic meaning of sharp/flat, major/minor and aug/dim, in that the former is always further fifthwards on the chain of fifths than the latter. Sharp is lower in pitch than flat, and major/aug is narrower than minor/dim. While this approach may seem bizarre at first, interval arithmetic and chord names work as usual. Furthermore, conventional 12edo music can be directly translated to 13edo "on the fly".

Degree	Cents	Up/down notation using the narrow 5th of 7\13, with major wider than minor			Up/down notation using the narrow 5th of 7\13, with major narrower than minor
0	0	perfect unison	P1	D	perfect unison	P1	D
1	92	up unison, minor 2nd	^1, m2	D^, E	up unison, major 2nd	^1, M2	D^, E
2	185	upminor 2nd, minor 3rd	^m2, m3	E^, Fb	upmajor 2nd, major 3rd	^M2, M3	E^, F#
3	277	downmajor 2nd, upminor 3rd	vM2, ^m3	E#v, Fb^	downminor 2nd, upmajor 3rd	vm2, ^M3	Ebv, F#^
4	369	major 2nd, downmajor 3rd	M2, vM3	E#, Fv	minor 2nd, downminor 3rd	m2, vm3	Eb, Fv
5	462	major 3rd, down 4th	M3, v4	F, Gv	minor 3rd, down 4th	m3, v4	F, Gv
6	554	perfect 4th, down 5th	P4, v5	G, Av	perfect 4th, down 5th	P4, v5	G, Av
7	646	up 4th, perfect 5th	^4, P5	G^, A	up 4th, perfect 5th	^4, P5	G^, A
8	738	up 5th, minor 6th	^5, m6	A^, B	up 5th, major 6th	^5, M6	A^, B
9	831	upminor 6th, minor 7th	^m6, m7	B^, Cb	upmajor 6th, major 7th	^M6, M7	B^, C#
10	923	downmajor 6th, upminor 7th	vM6, ^m7	B#v, Cb^	downminor 6th, upmajor 7th	vm6, ^M7	Bbv, C#^
11	1015	major 6th, downmajor 7th	M6, vM7	B#, Cv	minor 6th, downminor 7th	m6, vm7	Bb, Cv
12	1108	major 7th, down 8ve	M7, v8	C, Dv	minor 7th, down 8ve	m7, v8	C, Dv
13	1200	perfect 8ve	P8	D	perfect 8ve	P8	D

For alternative notations, see Ups and Downs Notation -"Supersharp" EDOs (pentatonic and octotonic fifth-based) and Ups and Downs Notation - Natural Generators (heptatonic second-based).

13 edo chromatic ascending and descending scale on C (MIDI)

13ed2-001.svg

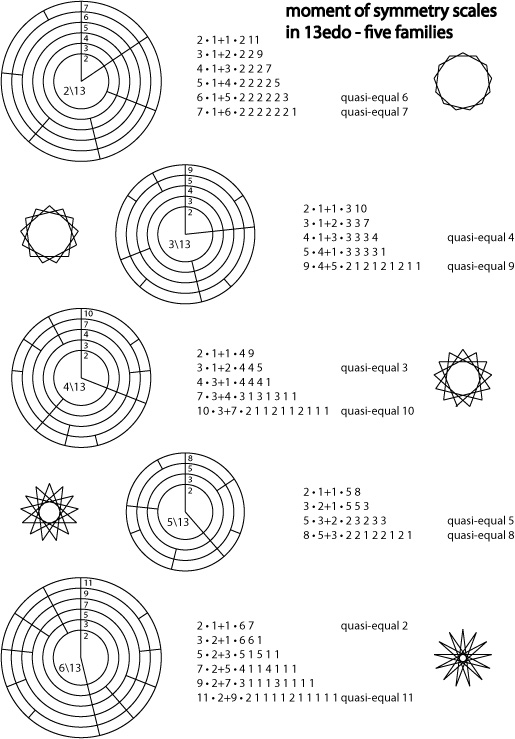
Scales in 13edo

Due to the prime character of the number 13, 13edo can form several xenharmonic moment of symmetry scales. The diagram below shows five "families" of MOS scales: those generated by making a chain of 2\13 (two degrees of 13edo), 3\13, 4\13, 5\13, & 6\13, respectively.

13edo horograms.pdf

~diagram by Andrew Heathwaite, based on horagrams pioneered by Erv Wilson

Another neat facet of 13-EDO is the fact that any 12-EDO scale can be "turned into" a 13-EDO scale by either adding an extra semitone, or turning an existent semitone into a whole-tone. Because of this, melody in 13-EDO can be quite mind-bending and uncanny, and phrases that begin in a familiar way quickly lead to something totally unexpected.

Harmony in 13edo

Contrary to popular belief, consonant harmony is possible in 13-EDO, but it requires a radically different approach than that used in 12-EDO (or other Pythagorean or Meantone-based tunings). Trying to approximate the usual major and minor triads of 12-EDO within 13-EDO is usually a disappointment if consonance is the goal; 0-3-7, 0-4-7, 0-3-8, and 0-4-8 are all rather rough in 13-EDO. Typically, the most consonant harmonies do not use a "stack of 3rds" the way they do in 12-TET, since the strongest dissonances in 13-EDO are near the middle of the octave (degrees 6, 7, and 8). Instead, a stack of whole-tones, or a mixture of whole-tones and minor 3rds, often yields good results. For example, one way to view 13-EDO is as a subgroup temperament of harmonics 2.5.9.11.13. It actually performs quite admirably in this regard, and a chord of 0-4-15-19-22 (approximating 4:5:9:11:13) sounds very convincing. An even larger subgroup is the 2*13 subgroup 2.9.5.21.11.13, on which 13 has the same tuning and commas as 26et.

By this, we can assume that the major ninth of 13edo can be thought of as analogous to the perfect fifth in 12edo and other meantone edos.This means that the major second or major ninth is the most consonant interval next to 2/1 in 13edo followed by 11/8, 5/4 and so on. The 4:5:9 chord can therefore be thought of as a possible basic harmonic triad in 13edo.

The 2.9.5.11.13 subgroup has commas 45/44, 65/64 and 81/80, leading to a linear temperament with POTE generator 185.728 cents, quite close to 2\13. Use this as a generator, and at 7 notes (6L1s) two full pentads are available (as well as two more 4:5:9:11 tetrad, and one 4:5:9:13 tetrad). These triads and tetrads can be assumed to likely be the most consonant base sonorities available in 13 edo and act in a similar way to major/minor triads. However, other sonorities such as Orwell chords are available as well.

Other approaches explored by specific composers and theorists are outlined further down, in the context of more complete tonal systems.

Play the 4:5:9 chord:

Play the 4:5:9:11 chord:

Play the 4:5:9:13 chord:

Play the 4:5:9:21 chord:

Notational and Compositional Approaches to 13edo

13edo has drawn the attention of numerous composers and theorists, some of whom have devoted some effort to provide a notation and an outline of a compositional approach to it. Some of these are described below.

The Cryptic Ruse Methods

13edo offers two main candidates for diatonic-like scales: the 6L1s heptatonic MOS generated by 2\13, and the 5L3s octatonic MOS. Both of these scales are Rothenberg proper, and bear a slightly-twisted resemblance to the 12edo diatonic scale. Specifically, the 6L1s scale resembles the 12edo diatonic with one of its semitones replaced with a whole-tone, while the 5L3s scale resembles the 12edo diatonic with an extra semitone inserted between two adjacent whole-tones.

To facilitate discussion of these scales, Cryptic Ruse has ascribed them names based on H.P. Lovecraft's "Dream Cycle" mythos. The 2\13-based heptatonic has been named "archeotonic" after the "Old Ones" that rule the Dreamlands, and the 5\13-based octatonic has been named "oneirotonic" after the Dreamlands themselves. Modes of the archeotonic are named after the individual Old Ones themselves; modes of the oneirotonic are named after cities in the Dreamlands.

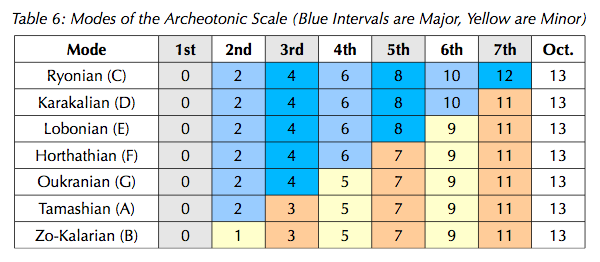
Modes and Harmony in The Archaeotonic Scale

A 7-nominal notation is proposed, using the letters A-G. The "C natural" scale is proposed to be degrees 0-2-4-6-8-10-12-(13), with the note "C" tuned to a reference pitch of concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13edo.

Treating 13edo as a temperament as proposed above leads to a chord of degrees 0-2-4-6-9 representing the JI harmony 8:9:10:11:13; two such pentads exist in this scale, on E and F. Smaller harmonic units exist as follows: 8:9:10:11 on C, D, E, and F; 8:9:10:13 on E, F and G; 8:9:10 on C, D, E, F, and G; 8:9:11 on C, D, E, and F; 8:9:13 on E, F, G, and A. Finally, on B we have the relatively-discordant 16:17:21:26 (0-1-5-9, or the notes B-C-E-G), which can be octave-inverted into a more concordant 8:13:17:21.

There may be other concordant harmonies possible in this scale that do not represent segments of the overtone series; further exploration is pending.

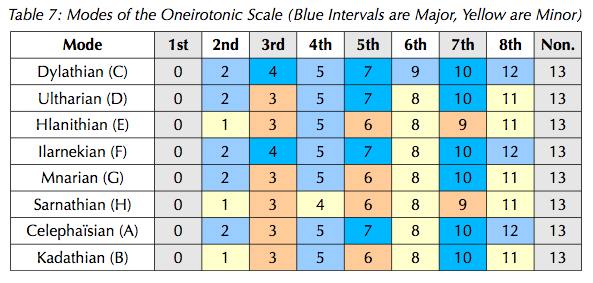
Modes and Harmony in the Oneirotonic Scale

Here an 8-nominal notation is proposed, using letters A-H. The "C natural" scale is proposed to be degrees 0-2-4-5-7-9-10-12-(13), with the note "C" tuned to concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13edo.

There is a great number of potential consonant harmonies in this scale. A dedicated article on harmony and tonality in the oneirotonic scale is forthcoming.

The Kentaku (aka William Lynch) Method for Octatonic Notation

Normally, 13edo can be notated by adding an accidental between E and F. For some reading the same staff with the same letters but in different places can be mind boggling and lead to confusion. That's why some have recommended different options.

13edo may be better suited to be notated by using the 8 notes of the MOS father[8] as the notes except that similarly to meantone, the 4th mode of Father[8] is the default "Basic" mode of 13edo and is notated with new letters. A new set of letters may benefit by giving 13edo a fresh perspective. William Lynch proposes using the letters JKLMNOPQ as the notes of the 4th mode of Father[8] with J being an 11/8 from a normal C, in order to give it a more personal identify rather than hearing it as C. The remaining letters of 13 edo are notated with sharps and flats like 12edo. The whole alphabet is written J-J#-K-K#-L-M-M#-N-N#-O-P-P#-Q-J . There are no accidentals between LM, OP, and QJ. The idea behind using the 4th mode rather than the 1st is that this mode contains a warmer sounding shape because it has a flat sixth instead of a natural one so William has chosen this to be the default mode rather than Dylathian.

This new approach simply modifies the way 13edo is systematized and notated but is based on the exact same 8 tone scale that Cryptic Ruse uses.

Notation written on the staff looks nearly the same as 12edo notation, except that because there are 8 letters instead of 7, the notes offset themselves to where space-to-space and line-to-line are now octaves rather than line-to-space. This makes learning the system much easier because a letter that is on a line is always on a line.

13EDO Chromatic Scale in Octatonic Notation:

Also, this approach allows for a circle of fourths to be produced:

Listen to Ryonian on J (F#):

Listen to Dylathian on J: (F#)

More on William Lynch's 13 EDO octatonic approach

Mapping to Standard Keyboards

The 5L+3s scale (Oneirotonic) can be mapped to the standard keyboard effectively, although somewhat awkwardly. Consider the sequence of 730-cent intervals that it derives from: 1 6 11 3 8 (13) 5 10 2 7 12 4 9 1/1. One of these must be absent, so it might as well be the last. So, there are at most five of the full octatonic scales on different keys. Of the four mappings that keep the major pentatonic on the white keys, which ironically look like ordinary minor-pentatonics, the latter which begins on B might be the most straightforward to learn and use.

1	6	11	3	8	(13)	5	10	2	7	12	4	9	1	Place in Chain of 738.5 cent intervals
X	*		*	*		*		*	*		*		X	Marked are the octatonic scales (X=Sarnathian)
	*		*	*		*		X	*		*	*
	*		X	*		*	*		*		*	*
	*	*		*		*	*		*		X	*
	*	*		*		X	*		*	*		*
D	Eb	E	F	Gb		G	Ab	A	Bb	B	C	Db	D	Keeps the pentatonic scale on the white keys
A	Bb	B	C	Db		D	Eb	E	F	Gb	G	Ab	A
E	F	Gb	G	Ab		A	Bb	B	C	Db	D	Eb	E
B	C	Db	D	Eb		E	F	Gb	G	Ab	A	Bb	B
C	Db	D	Eb	E		F	Gb	G	Ab	A	Bb	B	C	Puts the missing key between a semitone
G	Ab	A	Bb	B		C	Db	D	Eb	E	F	Gb	G	(if that were to be valuable in any way)

The archaeotonic tonality is much simpler to deal with: you just leave out a tone and remember which one. Although, for diatonic use it may be more convenient to put the missing tone between E/F or B/C to keep it on the white keys, with the remaining small step where it looks like it should be.

Commas

13 EDO tempers out the following commas. (Note: This assumes the val < 13 21 30 36 45 48 |.)

Comma	Monzo	Value (Cents)	Name 1	Name 2	Name 3
2109375/2097152	\| -21 3 7 >	10.06	Semicomma	Fokker Comma
1029/1000	\| -3 1 -3 3 >	49.49	Keega
525/512	\| -9 1 2 1 >	43.41	Avicennma	Avicenna's Enharmonic Diesis
64/63	\| 6 -2 0 -1 >	27.26	Septimal Comma	Archytas' Comma	Leipziger Komma
64827/64000	\| -9 3 -3 4 >	22.23	Squalentine
3125/3087	\| 0 -2 5 -3 >	21.18	Gariboh
3136/3125	\| 6 0 -5 2 >	6.08	Hemimean
121/120	\| -3 -1 -1 0 2 >	14.37	Biyatisma
441/440	\| -3 2 -1 2 -1 >	3.93	Werckisma

Animism

The animist comma, 105/104, appears whenever 3*5*7=13... 13edo does not approximate 3 and 7 individually (26edo does), but 13edo has 21/16 (=3*7) and is also an animist temperament. In 13edo, the 5th harmonic is tuned so flatly that 5/4 = 16/13, leading to some interesting identities. So two scales stand out through this construction:

0 4 5 8 9 13 pentatonic

and

0 1 3 4 5 8 9 10 12 13 nonatonic