Oneirotonic
The term oneirotonic (/oʊnaɪrəˈtɒnɪk/ oh-ny-rə-TON-ik or /ənaɪrə-/ ə-ny-rə-) is used for the 8-note MOS structure 5L 3s, whose brightest mode is LLsLLsLs. The name oneirotonic (from Greek oneiros 'dream') was coined by Cryptic Ruse after the Dreamlands in H.P. Lovecraft's Dream Cycle mythos. Oneirotonic is a distorted diatonic, because it has one extra small step compared to diatonic (5L 2s).
The generator size ranges from 450¢ (3\8) to 480¢ (2\5). Hence any edo with an interval between 450¢ and 480¢ has an oneirotonic scale. 13edo is the smallest edo with a (non-degenerate) 5L3s oneirotonic scale and thus is the most commonly used oneirotonic tuning.
In terms of regular temperaments, there are at least two melodically viable ways to interpret oneirotonic (analogous to diatonic having multiple temperament interpretations depending on generator size):
- When the generator is between 461.54¢ (5\13) and 466.67¢ (7\18): A-Team (13&18, a 4:5:9:21 or 2.9.5.21 temperament)
- When the generator is between 457.14¢ (8\21) and 461.54¢ (5\13): Petrtri (13&21, a 4:5:9:11:13:17 or 2.5.9.11.13.17 temperament)
13edo represents both temperaments.
There is also Buzzard, when the generator is between 471.42¢ (11\28) and 480¢ (2\5), but while this is a harmonically accurate temperament, with 4 generators reaching 3/2 and -3 generators 7/4, it is relatively weak melodically, as the optimum size of the small steps is around 20-25 cents, making it difficult to distinguish from equal pentatonic.
Tunings
A-Team tunings (with generator between 5\13 and 7\18) have L/s ratios between 2/1 and 3/1.
A-Team can be tuned by ear, by tuning a chain of pure harmonic sevenths and taking every other note. This corresponds to using a generator of 64/49 = 462.34819 cents. A chain of fourteen 7/4's are needed to tune the 8-note oneirotonic MOS. This produces a tuning close to 13edo.
The sizes of the generator, large step and small step of oneirotonic are as follows in various A-Team tunings.
| 13edo | 18edo | 31edo | 64/49 generator | POTE tuning | JI intervals represented (2.9.5.21 subgroup) | |
|---|---|---|---|---|---|---|
| generator (g) | 5\13, 461.54 | 7\18, 466.67 | 12\31, 464.52 | 462.35 | 464.14 | 21/16 |
| L (3g - octave) | 2\13, 184.62 | 3\18, 200.00 | 5\31, 193.55 | 187.04 | 192.42 | 9/8, 10/9 |
| s (-5g + 2 octaves) | 1\13, 92.31 | 1\18, 66.66 | 2\31, 77.42 | 88.26 | 79.30 | 21/20 |
Petrtri tunings (with generator between 8\21 and 5\13) have less extreme L-to-s ratios than A-Team tunings, between 3/2 and 2/1. The 8\21-to-5\13 range of oneirotonic tunings remains relatively unexplored.
The sizes of the generator, large step and small step of oneirotonic are as follows in various petrtri tunings.
| 13edo | 21edo | 34edo | POTE tuning | JI intervals represented (2.5.9.11.13.17 subgroup) | |
|---|---|---|---|---|---|
| generator (g) | 5\13, 461.54 | 8\21, 457.14 | 13\34, 458.82 | 459.15 | 13/10, 17/13, 22/17 |
| L (3g - octave) | 2\13, 184.62 | 3\21, 171.43 | 5\34, 176.47 | 177.45 | 10/9, 11/10 |
| s (-5g + 2 octaves) | 1\13, 92.31 | 2\21, 114.29 | 3\34, 105.88 | 104.25 | 18/17, 17/16 |
One petrtri tuning is golden oneirotonic, which uses 1200*(2-φ) = 458.3592135¢ as generator and has L/s = φ; it is the limit of taking generators in Fibonacci number edos 5\13, 8\21, 13\34, 21\55, 34\89,....
Notation
The notation used in this article is J Celephaïsian (LsLLsLLs) = JKLMNOPQJ (with J ≈ 180 Hz), unless specified otherwise. We denote raising and lowering by a chroma (L-s) by & "amp" and @ "at". (Mnemonics: & "and" means additional pitch. @ "at" rhymes with "flat".)
Thus the 13edo gamut is as follows:
J J&/K@ K L L&/M@ M M&/N@ N O O&/P@ P P&/Q@ Q J
Note: N is close to standard C, since the reference pitch 180 Hz for J was chosen to be nearly a pure 11/8 above standard 12edo C.
Intervals
| Generators | Notation (1/1 = J) | Octatonic interval category name | Generators | Notation of 2/1 inverse | Octatonic interval category name |
|---|---|---|---|---|---|
| The "diatonic" 8-note scale has the following intervals (from some root): | |||||
| 0 | J | perfect unison | 0 | J | octave |
| 1 | M | perfect mosfourth | -1 | O | perfect mossixth |
| 2 | P | major mosseventh | -2 | L | minor mosthird |
| 3 | K | major mossecond | -3 | Q@ | minor moseighth |
| 4 | N | major mosfifth | -4 | N@ | minor mosfifth |
| 5 | Q | major moseighth | -5 | K@ | minor mossecond |
| 6 | L& | major mosthird | -6 | P@ | minor mosseventh |
| 7 | O& | augmented sixth | -7 | M@ | diminished fourth |
| The "chromatic" 13-note scale also has the following intervals (from some root): | |||||
| 8 | J& | augmented unison | -8 | J@ | diminished octave |
| 9 | M& | augmented mosfourth | -9 | O@ | diminished mossixth |
| 10 | P& | augmented mosseventh | -10 | L@ | diminished mosthird |
| 11 | K& | augmented mossecond | -11 | Q@@ | diminished moseighth |
| 12 | N& | augmented mosfifth | -12 | N@@ | diminished mosfifth |
Key signatures
Flat keys:
- J@ Celephaïsian, L@ Dylathian = Q@, N@, K@, P@, M@, J@, O@, L@
- M@ Celephaïsian, O@ Dylathian = Q@, N@, K@, P@, M@, J@, O@
- P@ Celephaïsian, J@ Dylathian = Q@, N@, K@, P@, M@, J@
- K@ Celephaïsian, M@ Dylathian = Q@, N@, K@, P@, M@
- N@ Celephaïsian, P@ Dylathian = Q@, N@, K@, P@
- Q@ Celephaïsian, K@ Dylathian = Q@, N@, K@
- L Celephaïsian, N@ Dylathian = Q@, N@
- O Celephaïsian, Q@ Dylathian = Q@
All-natural key signature:
- J Celephaïsian, L Dylathian = no sharps or flats
Sharp keys:
- M Celephaïsian, O Dylathian = L&
- P Celephaïsian, J Dylathian = L&, O&
- K Celephaïsian, M Dylathian = L&, O&, J&
- N Celephaïsian, P Dylathian = L&, O&, J&, M&
- Q Celephaïsian, K Dylathian = L&, O&, J&, M&, P&
- Enharmonic with J@ Celeph., L@ Dylath. in 13edo
- L& Celephaïsian, N Dylathian = L&, O&, J&, M&, P&, K&
- Enharmonic with M@ Celeph., O@ Dylath. in 13edo
- O& Celephaïsian, Q Dylathian = L&, O&, J&, M&, P&, K&, N&
- Enharmonic with P@ Celeph., J@ Dylath. in 13edo
- J& Celephaïsian, L& Dylathian = L&, O&, J&, M&, P&, K&, N&, Q&
- Enharmonic with K@ Celeph., M@ Dylath. in 13edo
Modes
Oneirotonic modes are named after cities in the Dreamlands.
- Dylathian: LLSLLSLS
- Ilarnekian: LLSLSLLS
- Celephaïsian: LSLLSLLS (Easley Blackwood's 13-note etude uses this as its home mode.)
- Ultharian: LSLLSLSL (A kinda-sorta Dorian analogue. Depending on your purposes, a better Dorian analogue may be the MODMOS LSLLLSLS; see the section on oneiro MODMOSes below.)
- Mnarian: LSLSLLSL
- Kadathian: SLLSLLSL
- Hlanithian: SLLSLSLL
- Sarnathian: SLSLLSLL
The modes on the white keys JKLMNOPQJ are:
- J Celephaïsian
- K Kadathian
- L Dylathian
- M Ultharian
- N Hlanithian
- O Ilarnekian
- P Mnarian
- Q Sarnathian
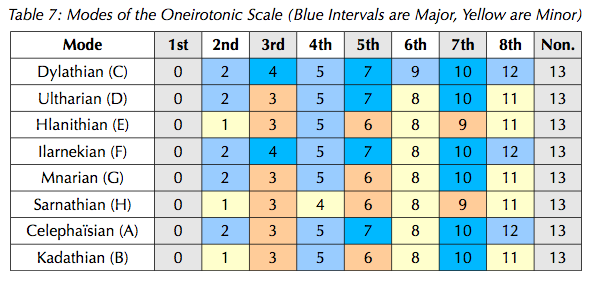
The modes in 13edo edo steps and C-H notation:
Pseudo-diatonic theory
Oneirotonic is often used as distorted diatonic. Because distorted diatonic modal harmony and functional harmony both benefit from a recognizable major third, the following theory essentially assumes an A-Team tuning, i.e. an oneirotonic tuning with generator between 5\13 and 7\18 (or possibly an approximation of such a tuning, such as a neji). One should experiment and see how well these ideas work in other oneirotonic tunings.
Ana modes
We call modes with a major mos5th ana modes (from Greek for 'up'), because the sharper 5th degree functions as a flattened melodic fifth when moving from the tonic up. The ana modes of the MOS are the 4 brightest modes, namely Dylathian, Ilarnekian, Celephaïsian and Ultharian.
The ana modes have squashed versions of the classical major and minor pentachords R-M2-M3-P4-P5 and R-M2-m3-P4-P5 and can be viewed as providing a distorted version of classical diatonic functional harmony and counterpoint. For example, in the Dylathian mode, the 4:5:9 triad on the sixth degree can sound like both "V" and "III of iv" depending on context. Basic chord progressions can move by perfect mosfourths, thirds, or major seconds: for example, J major-M minor-P minor-Ob major-J major (in Ilarnekian) or J major-K major-O major-M major-J major (in Dylathian).
In pseudo-classical functional harmony, the 6th scale degree (either an augmented mossixth or a perfect mossixth) could be treated as mutable. The perfect mossixth would be used when invoking the diatonic V-to-I trope by modulating by a perfect mosfourth from the sixth degree. The augmented mossixth would be used when a major key needs to be used on the fourth degree.
Kata modes
We call modes with a minor mos5th kata modes (from Greek for 'down'). The kata modes of the MOS are the 4 darkest modes, namely Mnarian, Kadathian, Hlanithian and Sarnathian. In kata modes, the melodically squashed fifth from the tonic downwards is the flatter 5th degree. Kata modes could be used to distort diatonic tropes that start from the tonic and work downwards or work upwards towards the tonic from below it. For example:
- Mnarian (LSLSLLSL) and Kadathian (SLLSLLSL) are kata-Mixolydians
- Hlanithian (SLLSLSLL) is a kata-melodic major (the 4th degree sounds like a major third; it's actually a perfect mosfourth.)
- Sarnathian (SLSLLSLL) is a kata-melodic minor (When starting from the octave above, the 4th degree sounds like a minor third; it's actually a diminished mosfourth.)
When used in an "ana" way, the kata modes are radically different in character than the brighter modes. Because the fifth and seventh scale degrees become the more consonant minor tritone and the minor sixth respectively, the flat tritone sounds more like a stable scale function. Hlanithian, in particular, is a lot like a more stable version of the Locrian mode in diatonic.
MODMOSes
The most important oneirotonic MODMOS is LSLLLSLS (and its rotations), because it allows one to evoke certain ana or kata diatonic modes where three whole steps in a row are important (Dorian, Phrygian, Lydian or Mixo) in an octatonic context. The MOS would not always be able to do this because it has at most two large steps.
- LLLSLSLS: Dylathian &4: Ana-Lydian
- LLSLSLSL: Ilarnekian @8: Ana-Mixolydian
- LSLLLSLS: Celephaïsian &6: Ana-Dorian
- SLLLSLSL: Ultharian @2: Ana-Phrygian
- SLSLSLLL: Sarnathian @6: Kata-Locrian
- SLSLLLSL: Sarnathian &6: Kata-Dorian
- LSLSLLLS: Mnarian &8: Kata-Ionian
- LSLSLSLL: Hlanithian &2: Kata-Aeolian
Other potentially interesting oneirotonic MODMOSes (that do not use half-sharps or half-flats) are:
- the distorted harmonic minor LSLSLLSAS (A = aug 2nd = L + chroma)
- the distorted Freygish SASLSLLS
"Oneirotonic maqam"
The following assumes an edo with A-Team oneirotonic scales and oneirotonic neutral seconds, such as 18edo and 26edo.
Zheanist theory
A-Team oneirotonic may be a particularly good place to apply Zheanism, because A-Team temperament doesn't yield many low-complexity chords.
18edo may be a better basis for a style of oneirotonic Zheanism using comma sharp and comma flat fifths (in particular diesis sharp and diesis flat fifths; diesis is a category with a central region of 32 to 40c) than 13edo. In 18edo both the major fifth (+31.4c) and the minor fifth (-35.3) are about a diesis off from a just perfect fifth. In 13edo only the major fifth is a diesis sharp, and it is +36.5c off from just; so there's less wiggle room for a neji if you want every major fifth to be at most a diesis sharp).
31nejis and 34nejis also provide opportunities to use dieses directly, since 1\31 (38.71c) and 1\34 (35.29c) are both dieses.
Chords
These are just oneirotonic-inspired chords, they aren't guaranteed to fit in your neji.
/13
- 13:16:19 Tridecimal Squashed Major Triad
- 13:17:19 Tridecimal Squashed Sus4
- 13:17:20 Tridecimal Squashed 2nd Inversion Minor Triad
- 13:17:21 Tridecimal Squashed 2nd Inversion Major Triad
- 13:16:19:22 Tridecimal Oneiro Major Tetrad
/17
- 17:20:25 Septen Squashed Minor Triad
- 17:20:26 Septen Squashed 1st Inversion Major Triad
- 17:20:25:29 Septen Minor Oneiro Tetrad
- 17:21:25:29 Septen Major Oneiro Tetrad
- 17:20:26:29 Septen Squashed 1st Inversion Major Triad addM6
- 34:40:47:55 Septen Orwell Tetrad
- 34:40:52:58:76:89:102:129 (Celephaïsian + P5; R-min3-sup5-M6-M9-sub11-P12(fc)-M14)
- 34:40:52:58:76:89:102:110:129 (Celephaïsian + P5; R-min3-sup5-M6-M9-sub11-P12(fc)-supmin13-M14)
- 34:40:50:58:89:102:129 (R-min3-sub5-M6-M9-sub11-P12(rc)-M14)
- 34:40:50:58:89:102:110:129 (R-min3-sub5-M6-M9-sub11-P12(rc)-supmin13-M14)
- 34:40:50:58:76:89:110:129 (R-m3-sub5-M6-M9-sub11-supm13-M7)
- 34:40:50:58:76:89:102:110:129:208 (R-m3-sub5-M6-M9-sub11-P12(rc)-supm13-M14-sup19(rc^2))
/23
- 23:27:30 Vice Squashed Min4
- 23:27:30:35:44 Vice Squashed Min4 addM5,M7
- 23:27:37 Vice Orwell Tetrad no5
- 46:54:63:76 Vice Orwell Tetrad
- 46:54:67:78 Vice Minor Oneiro Tetrad
- 46:54:60:67:78 Vice Min4 Oneiro Pentad
/29
- 29:34:38 Vicenon Squashed Sus4
- 29:34:42 Vicenon Squashed Minor Triad
- 29:36:42 Vicenon Squashed Major Triad
- 29:34:40:47 Vicenon Orwell Tetrad
- 29:38:65:84:99 Vicenon Oneiro Core Pentad
- 29:38:65:84:99:110 Vicenon Oneiro Core Hexad
- 58:65:72:80:84:94:99:110:116 Vicenon Dylathian &4
- 58:65:72:76:84:94:99:110:116 Vicenon Dylathian
- 58:65:72:76:84:89:99:110:116 Vicenon Ilarnekian
- 58:65:72:76:84:89:99:104:116 Vicenon Ilarnekian @8
- 58:65:68:76:84:94:99:110:116 Vicenon Celephaïsian &6
- 58:65:68:76:84:89:99:110:116 Vicenon Celephaïsian
- 58:65:68:76:84:89:99:104:116 Vicenon Ultharian
- 58:65:68:76:80:89:99:104:116 Vicenon Mnarian
- 58:65:68:76:80:89:99:110:116 Vicenon Mnarian &8
- 58:65:68:76:80:89:94:104:116 Vicenon Hlanithian &2
- 58:61:68:76:80:89:99:104:116 Vicenon Kadathian
- 58:61:68:76:84:89:99:104:116 Vicenon Ultharian @2
- 58:61:68:76:80:89:94:104:116 Vicenon Hlanithian
- 58:61:68:72:80:89:99:104:116 Vicenon Sarnathian &6
- 58:61:68:72:80:89:94:104:116 Vicenon Sarnathian
- 58:61:68:72:80:84:94:104:116 Vicenon Sarnathian @6
Over small prime multiples
Some oneirotonic nejis
- 58:61:65:68:72:76:80:84:89:94:99:104:110:116 A very low-complexity 13neji; not optimized for transposability.
Temperament interpretations
A-Team (13&18, 4:5:9:21)
EDOs that support A-Team include 13edo, 18edo, and 31edo.
- 18edo can be used if a large L/s ratio of 3 is desired (thus 18edo oneirotonic is distorted 17edo diatonic).
- 31edo can be used if a near-just 5/4 is desired.
Intervals
Sortable table of Dylathian, the brightest mode:
| Degree | Size in 13edo | Size in 18edo | Size in 31edo | Note name on L | Approximate ratios[1] | #Gens up |
|---|---|---|---|---|---|---|
| 1 | 0\13, 0.00 | 0\18, 0.00 | 0\31, 0.00 | L | 1/1 | 0 |
| 2 | 2\13, 184.62 | 3\18, 200.00 | 5\31, 193.55 | M | 9/8, 10/9 | +3 |
| 3 | 4\13, 369.23 | 6\18, 400.00 | 10\31, 387.10 | N | 5/4 | +6 |
| 4 | 5\13, 461.54 | 7\18, 466.67 | 12\31, 464.52 | O | 21/16, 13/10 | +1 |
| 5 | 7\13, 646.15 | 10\18, 666.66 | 17\31, 658.06 | P | 13/9, 16/11 | +4 |
| 6 | 9\13, 830.77 | 13\18, 866.66 | 22\31, 851.61 | Q | 13/8, 18/11 | +7 |
| 7 | 10\13, 923.08 | 14\18, 933.33 | 24\31, 929.03 | J | 12/7 | +2 |
| 8 | 12\13, 1107.69 | 17\18, 1133.33 | 29\31, 1122.58 | K | +5 |
- ↑ The harmonics over 1/1 are in bold. The ratio interpretations that are not valid for 18edo are italicized.
Petrtri (13&21, 4:5:9:11:13:17)
The three major edos in this range, 13edo, 21edo and 34edo, all nominally support petrtri, but 34edo is close to optimal for the temperament, with a generator only .33c flat of the optimal (POTE) petrtri generator of 459.1502c. Close-to-optimal petrtri tunings such as 34edo may be particularly useful for the Sarnathian mode, as Sarnathian in these tunings uniquely approximates four over-2 harmonics plausibly, namely 17/16, 5/4, 11/8, and 13/8.
Intervals
Sortable table of Dylathian, the brightest mode:
| Degree | Size in 13edo | Size in 21edo | Size in 34edo | Size in POTE tuning | Note name on L | Approximate ratios | #Gens up |
|---|---|---|---|---|---|---|---|
| 1 | 0\13, 0.00 | 0\21, 0.00 | 0\34, 0.00 | 0.00 | L | 1/1 | 0 |
| 2 | 2\13, 184.62 | 3\21, 171.43 | 5\34, 176.47 | 177.45 | M | 10/9, 11/10 | +3 |
| 3 | 4\13, 369.23 | 6\21, 342.86 | 10\34, 352.94 | 354.90 | N | 11/9, 16/13 | +6 |
| 4 | 5\13, 461.54 | 8\21, 457.14 | 13\34, 458.82 | 459.15 | O | 13/10, 17/13, 22/17 | +1 |
| 5 | 7\13, 646.15 | 11\21, 628.57 | 18\34, 635.294 | 636.60 | P | 13/9, 16/11 | +4 |
| 6 | 9\13, 830.77 | 14\21, 800.00 | 23\34, 811.77 | 814.05 | Q | 8/5 | +7 |
| 7 | 10\13, 923.08 | 16\21, 914.29 | 26\34, 917.65 | 918.30 | J | 17/10 | +2 |
| 8 | 12\13, 1107.69 | 19\21, 1085.71 | 31\34, 1094.12 | 1095.75 | K | 17/9, 32/17 | +5 |
Samples
(A rather classical-sounding 3-part harmonization of the ascending J Ilarnekian scale; tuning is 13edo)
(13edo, first 30 seconds is in J Celephaïsian)
(13edo, L Ilarnekian)
(by Igliashon Jones, 13edo, J Celephaïsian)