Talk:Patent val

This page also contains archived Wikispaces discussion.

306c

c? what? 306edo takks about 306c?z! PiotrGrochowski (talk) 07:07, 19 September 2018 (UTC)

proposal to rename "patent val" to "simple map"

My first concern with “patent” map is that "patent", as an adjective, is unfamiliar to most people, unless it relates to those documents called patents. Calling them "obvious maps" would have been better than "patent maps".

The second concern is that they are not always obvious. If it were, there would be no contention about it. This name suggests a positive value judgment (and dismissive value judgement on other maps) which we think is inappropriate. A name like “patent” or "obvious" map may lead too many people concerned with accurate tuning to accept this map when if they'd known better they may have preferred the map with the most accurate tuning overall, i.e. the “best” map. The classic example of a best map which is not the patent map is 17c at the 5-limit.

These concerns arose in recent public discussion I was involved in, and it was agreed at that time that "naive" was an apt replacement for "patent". But through further discussion, we decided that this would have the opposite problem: where "patent" had excessively positive connotations, "naive" would have had inappropriately negative connotations, and might run the risk of discouraging people from using them despite such maps being relatively good. So we concluded that a word with more neutral connotations was appropriate, and so we're going with "simple". These maps may not always be obvious, but they are always simple to calculate.

The "simple map" sets octaves pure, and then for each other prime harmonic individually, chooses the nearest mapping (the one with least error). That's clearly simple, and it's good, but it's not necessarily best. On the other hand, the best map is not strictly defined yet, but it would have a more elaborate definition, involving a consideration of errors in the ratios between primes, not only in the primes themselves. --Cmloegcmluin (talk) 23:27, 25 September 2021 (UTC)

I think your first two points somewhat neutralize each other. If people are unfamiliar with the word, no connotation could arise. Otherwise, if people feel positive with the word, they already know what it means.

To me, patent in the sense of obvious is rather literary, which is suitable for carrying complex or subtle meanings, and effectively stay clear of any connotations. Simple map is a combo of two everyday words and gives me the impression that the concept isn't rigorously defined. If I must choose such a term, it'd be Kite's nearest edomapping. Nearest is more informative than simple at least.

I also oppose using naive as a substitute. That word should be reserved for direct approximation. FloraC (talk) 18:01, 26 September 2021 (UTC)

Thanks for for your reply, FloraC. I'll reply to your points in reverse order.

Re: "naive". I agree. Your point — about direct approximation being a more appropriate candidate for that word — is an interesting additional reason not to use naive here. (To be clear, I was not advocating for it at this point; I merely mentioned it as one thing that was discussed in the past.)

Re: how "patent" being a less everyday word than "obvious" may actually be advantageous, by better connoting that the thing defined is a specially defined thing: I totally get what you mean there. In fact, I made that point myself during some discussion! That said, this issue of "patent vs. obvious" is superseded by the fact that I think neither "patent" nor "obvious" are appropriate words for this term. This leads me to your first point, where it looks like you've misunderstood my original post (probably my fault! though I haven't been able to come up with a guess as to how you've misread it).

You say that my first two points somewhat neutralize each other, but I think that must be because you've misunderstood my second point (which is conveyed in my second paragraph). What I was trying to say about 17-ET in the 5-limit was that it's hard to say which of its maps would be "the" obvious/patent one to use. The simplest/nearest-edomapping one is ⟨17 27 39] but the best one by many common standards is instead ⟨17 27 40]. So which one is obvious/patent — the simple/near one, or the best one? My point is that neither can be said to be obvious/patent. Maybe to one person one is obvious, but to another person the other is obvious. And so if there's any disagreement at all, no one gets to claim obvious (while probably everyone could agree which one of them was simple). And I further say that 17-ET is not an isolated example, and that this lack of consistent patentness/obviousness sufficiently problematizes the use of either word, patent or obvious.

You do make an excellent point, however, about how "nearest" carries more helpful information than "simple", though. How do you feel about "nearest map", then? I ask because this term is always used in reference to an EDO/ET, so I'm not certain what "edomapping" brings to the table that "map" doesn't already, while I would penalize it for being jargony where "map" is an established linear algebra term. --Cmloegcmluin (talk) 02:27, 27 September 2021 (UTC)

I believe edomapping is supposed to be a substitute for val, referring to an individual line of the map.

Nearest val/map is fine and it's already there. Yet if you mean by renaming to replace every instance of patent val on this wiki, I suspect that's beyond practical. Consider all the legacies, for example, the p in the wart notation. (I, for one, also don't plan to change my idiolect until a majority of people has made the transition.) FloraC (talk) 22:16, 27 September 2021 (UTC)

Additionally, it probably isn't favorable to replace val by map. Which word is more common in RTT? I suppose it's map. So unless val is deprecated completely as a term, we should be using it more so as to make it familiar to people. This corresponds to the consequence that increasing its use rate means increasing the Shannon entropy of our RTT terms set. FloraC (talk) 22:51, 27 September 2021 (UTC)

Thanks for clarifying the meaning of edomapping. In the parlance I recommend, "map" is already the word for an individual line of a mapping. "Map" is my substitute for "val". So a "mapping" is a matrix like {{vector|⟨12 19 28] and a "map" is a covector like ⟨12 19 28]. I don't think that's popular parlance but I think it works well and I would like to popularize it.

I'm glad you find "nearest map" to be fine. Would you agree I should alter my proposal from "simple map" to "nearest map" and you would find it acceptable, then?

I don't understand what you mean, however, by "['nearest map'] is already there". My guess was that you meant that it's already a common usage. But I don't find any hits for "nearest map" or "nearest val" anywhere on the wiki or the Discord server. Perhaps there's evidence elsewhere, such as on Facebook, but I'm not sure how to search it effectively. Or what did you mean exactly by that?

I do not mean to replace every instance of "patent val" on the wiki, for the reason you describe: impracticality. I would wish that over time some may naturally be supplemented with a parenthetical or outright replaced, and I would likely contribute gradually to the effort myself, but even if I was willing to do that amount of effort, I don't think it's right to force the issue on the community like that. My goal is not simply to change how people read this stuff, but to help improve how they think about it. I totally respect your choice to keep your idiolect close to the majority (and also, that's a cool word, "idiolect"...)

I note, however, that the "p" used in wart notation does not actually stand for "patent". Well, of course, it can be made to, but my point is that the man who designed wart notation, Graham Breed, did not intend it to stand for patent. In fact, he dislikes the term "patent" as well. He meant for the p in wart notation to stand for "prime", as he explained in this recent Facebook post: https://bit.ly/3ocLPKJ Anyway, I don't blame you for assuming that. I assumed it myself, until I heard it from him directly, and at first was quite taken aback!

The val vs map issue is another topic, certainly. I assume you made a mistake in the above and meant to say you suppose that "val" is more popular? I would agree. And as an extremely rough measure I searched for the count of pages that contain "val" vs. the count that contain "map" and there's over 1000 with val while only around 300 with map, which doesn't surprise me at all. In fact, I would say that I expected it to be even more lopsided, and expect that a lot of those usages of "map" are as verbs, like A maps to B. I don't understand your point about Shannon entropy exactly, but it sounds interesting, so please clarify if you'd like. I think I get the gist of your point, though, that if val is more popular, and we don't have good reason to deprecate it, then we should rally around it as a community, rather than splinter off into clusters that advocate for one of several different terms, confusing the issue overall for everyone on average.

I do have what I think is good reason to deprecate val in favor of map, though: "val" creates an unnecessary barrier to understanding for newcomers to RTT, who in the long run — assuming the community continues to grow, which I believe we all hope it should — will constitute the vast majority. Many newcomers to RTT are already familiar with established terms for the concepts RTT borrows from linear algebra. Even if "val" does have some connection to the mathematical concept of a "valuation", this is of no help in illuminating its music-theory meaning, which is simply that of being a mapping from a single generator to primes. The first sentence in the Xenharmonic Wiki article for "val" says, "a val is a linear map". And the first sentence of the Wikipedia article where "covector" redirects to is: "... a covector is a linear map from a vector space to its field of scalars". So that is why I prefer "map" to "val". --Cmloegcmluin (talk) 01:59, 28 September 2021 (UTC)

Yes, edomapping is supposed to be a substitute for val. Obvs I vote for nearest over simple/patent/obvious. I strongly agree that "val" creates an unnecessary barrier to understanding. Map or mapping is much better. I personally like edomapping even more because it is extremely self-explanatory. In a phrase like "the nearest edomapping for 17-edo" it is indeed redundant, but there I would just say "the nearest mapping for 17-edo". See also my comment below in "Uniform map". --TallKite (talk) 07:04, 28 September 2021 (UTC)

By "it's already there" I was saying that nearest edomapping is in the first sentence of this article. And we're ready to propagate this term to other pages once the val vs map issue is resolved.

So, no, I meant to say map was more popular. Val mainly arises in edos whereas map arises in higher-rank temps. The search giving more results of vals may be attributed to the template. Hence the number of search results can't be evidence for use rates. The Shannon entropy argument is based on the premise that val is a word of below-average use rate so increased use rate makes the communication more efficient – interesting indeed as it may be a theoretical basis for the keep-people-familiar argument. FloraC (talk) 09:15, 28 September 2021 (UTC)

Hi Kite, thanks for joining this thread!

Re: edomapping. Kite, we have different rankings of the terms. I would certainly rank your term "edomapping" way above "val", for the reason you give: it doesn't create a barrier to understanding. It's descriptive, which is something I fight for in terminology (and why I can see value in "nearest" over "simple"). But I still don't like it quite as much as "map" because it's a word that was made-up for xen, and so to a newcomer it will look weird and unfamiliar. We have a problematically off-putting amount of jargon in this domain, and terms like "edomapping" contribute to that. Also, "map" has better generalizable use; edomapping doesn't work for maps that don't include the octave, e.g. we could say ⟨13 19 23] is the nearest map for 13-ED3, but we couldn't say it was the nearest edomapping.

Re: "it's already there". I see, FloraC. You meant only the word "nearest" was already there. Right. Then indeed I agree that the term is ready for propagation, once the val vs map issue is resolved, although I would revise that last clause because it looks like it's actually the val vs map vs edomapping issue.

But first I would like to give Dave Keenan a chance to chime in here, because he was the one who originally came up with "simple map". I know that he is generally amenable to the types of arguments given here for "nearest" over "simple", so I have some confidence that he'll like it, but personally I owe it to him to solicit his opinion directly. So I've just emailed him about this.

Re: the relative popularity of map and val. Ah! Very interesting. I'm sorry that I guessed you had mistyped. I can see that two factors came together to lead me to assume you had accidentally written that "map" was more popular when you meant "val": 1) the amount of time I spend on Facebook and email with old-school RTT people who are steeped in Gene's jargon, where I am overwhelmingly exposed to "val" and in the minority of "map" users, and 2) my guess re: the meaning of this unfamiliar Shannon Entropy concept, which — due to some bad intuitions of mine — seems to be the exact opposite of what it really means (more on that in a bit). I hope you understand.

Well, I'm encouraged to hear that what you actually think is that "map" is the one which is more popular; that tells me that the community is moving in the direction I prefer. I agree that many of the occurrences of "val" are coming from the template, but I had permitted those as evidence of popularity, at least insofar as people are regularly exposed to it and accepting of it. Anyway, I did say it was only an incredibly rough estimate, though, and I only said it that way when I assumed I was using it to help your case. :) But if it's only hurting both of our cases, then of course, for similar reasons, I am willing to go ahead and agree with you that it can't really be used for evidence here. (By the way, it is also heartening to know that the template has gotten enough buy-in that we could accomplish a lot of patent val -> something better by changing things at one single point!)

Re: the Shannon Entropy thing. What I'm trying to say about my bad intuitions is this. I think that a situation where we have 2 terms we each use about half of the time or 3 terms we each use about a third of the time is a bad situation. I thought that was common sense, and so I assumed Shannon Entropy might be a fancy name for that idea (and here's a great piece of evidence where jargon and non-descriptive, in this case eponymous naming are creating a barrier to my understanding). I assumed that everyone would prefer standardization: a situation where we use a single term for a single thing almost all of the time and any other terms almost never. But if I'm understanding correctly now, it sounds like you're saying that we should strive for the situation where all of the words are used equally often? I'm probably still missing some important information, though. And I can't find any information about this "keep-people-familiar argument" concept you mention to help me make sense of it either. Sorry. If you want to convey these ideas to me more effectively, I would ask you to unpack these unfamiliar concepts for me, or find a simpler way that doesn't involve them. --Cmloegcmluin (talk) 16:22, 28 September 2021 (UTC)

I understand what I'm tryna argue is counterintuitive. Maybe I failed to make the context clear. It's this: val can't be replaced entirely by map. You can replace this word in the phrase patent val, but beyond this phrase, it can't be replaced by all occurrences. It turns up in all the temp pages, for example, where simply replacing the lines of vals to maps isn't appropriate. It has to do with the concern that val isn't totally synonymous with map. Val or edomapping (I reckon these two are synonymous) emphasises itself being an individual row of the map. Therefore, val remains a word that's likely to be encountered by those who work with RTT even if it's removed from the phrase patent val. That's why we hope to keep people familiar with both terms by using the term of lower use rate more, which can be explained through Shannon entropy. FloraC (talk) 01:26, 29 September 2021 (UTC)

proposal to rename "generalize patent val" to "uniform map"

My main concern with the term "generalized patent val", or GPV, is that it gets things backwards: it posits the GPV as a type of patent val, when it makes more sense to think of it the other way around, with the patent val as a type of GPV.

The present definition of GPV on the wiki bends over backwards to make its way work, essentially using non-integer EDOs, which are a contradiction in terms. Consider this alternative definition, however, which is more straightforward:

A GPV is any relatively near-just map found by uniformly multiplying the generators for JI (⟨log₂2 log₂3 log₂5 ... ]) by any value before rounding it to integers. For example, choosing 17.1, we find the map 17.1⟨1 1.585 2.322] = ⟨17.1 27.103 39.705] which rounds to ⟨17 27 40]. This is one of the many GPVs for 17-EDO, and every EDO has many possible GPVs. To find a GPV for n-EDO, choose any multiplier that rounds to n; another example for 17-EDO could be 16.9⟨1 1.585 2.322] = ⟨16.9 26.786 39.241] which rounds to ⟨17 27 39].

The key element in this definition is the uniform multiplier, and from it we draw our proposed replacement name for this structure: a uniform map. So the definition could be:

A uniform map is any relatively near-just map found by uniformly multiplying the generators for JI (⟨log₂2 log₂3 log₂5 ... ]) by any value before rounding it to integers. For example, choosing 17.1, we find the map 17.1⟨1 1.585 2.322] = ⟨17.1 27.103 39.705] which rounds to ⟨17 27 40]. This is one of the many uniform maps for 17-EDO, and every EDO has many possible uniform maps. To find a uniform map for n-EDO, choose any multiplier that rounds to n; another example for 17-EDO could be 16.9⟨1 1.585 2.322] = ⟨16.9 26.786 39.241] which rounds to ⟨17 27 39].

Any uniform map whose multiplier is an integer — or "integer uniform map" — is always the patent val (or simple map, per my other proposal above) for the corresponding EDO. And every simple map is also an integer uniform map. These are just two different helpful ways of thinking about the same structure; in contexts pertaining to tuning accuracy, "simple map" works great, and in contexts pertaining to other uniform maps, "integer uniform map" works great. --Cmloegcmluin (talk) 23:27, 25 September 2021 (UTC)

The definition may use some readability improvements but ultimately it's just wordplays. Your alternative definition still involves non-integer edos. Or what else do you think the multiplier is? Imagine a ruler with a varying scale put on the pitch continuum. 17 means that the octave is at the 17th point, implying there are 17 unit intervals between the starting point and the octave, which means 17edo. And therefore 17.1 means 17.1edo. FloraC (talk) 18:01, 26 September 2021 (UTC)

Thanks for your reply here too, FloraC.

If you mean to say that the multiplier in my definition is literally equivalent to a non-integer EDO, then I disagree with that. I think it is completely reasonable to interpret this multiplier as just that: a decimal number being multiplied against the JIP, as a step in a technique for finding this specific type of ET map. This conceptualization bypasses any notion of non-integer EDO. I do understand the mathematical reality of this situation quite comfortably, and I am not being willfully obtuse about this, so I could certainly concede that if someone wanted to think about non-integer EDOs while reading my definition, they still could find a way to do so. In other words: I recognize that these ideas are closely related. But it is quite important to me that I've managed to avoid explicitly using the phrase "non-integer EDO", because I believe that the way of thinking about the problem involving that contradiction in terms is unhelpful and perhaps harmful.

But I don't intend to dwell on that matter, which is mostly along the lines of what I would consider to be, in your words, merely a "readability improvement." The item of primary interest to me here is not the articulation of the definition, but the name for the term itself. I'm more concerned about replacing "generalized patent val" with "uniform map". I was only using the cleanliness of this definition relative to the existing definition as one argument in favor of that rename.

So, what I'm most curious about is: do you agree that this structure is better understood not as a generalization of the "simple map"/"patent val" structure, but that it's more accurately understood the other way around, with the "simple map"/"patent val" being a specific kind of this? I am quite interested in your perspective on that issue. --Cmloegcmluin (talk) 02:27, 27 September 2021 (UTC)

There's no reason to introduce the entity of a "decimal number multiplied against the jip", and if you do it, it needs an explanation. That's to ask what it is. The answer is the division number as illustrated by our ruler. Besides, you worded like avoiding explicit use of non-integer edos is an achievement, which I don't exactly agree, and to me this attempt sounds forced. In particular, I don't agree that non-integer edos involve contradiction. It's the same cognitive process as how people learn division: we first divide things by integers, and then we learn to extend the divisors to non-integers. Does division by a non-integer divisor involve contradiction? It doesn't.

The cognitive process I mentioned above therefore leads to the reason why generalized patent val is friendly to our minds. Moreover, I like that the relationship between patent val and generalized patent val is demonstrated by the name in that one contains the other. FloraC (talk) 22:16, 27 September 2021 (UTC)

We disagree about how best to explain this concept. You've convinced me that there is some virtue to the existing way of explaining it that's in the article. So I retract my proposal to replace it. Perhaps you would allow that — if I made some revisions to my way as you've recommended — there would be room for including my way of explaining it too. Eventually. But again this not my main interest here, so I'll drop the issue for now.

You've also convinced me to stop using the phrase "contradiction in terms" with respect to "non-integer EDOs". You're totally correct. Sorry for resisting, and thanks for explaining your take on that.

I'd like to call your attention to a point that I made in the original post which is that an "integer uniform map" is exactly equivalent to a "simple map"/"patent val" for the given integer. This to me is how best to achieve one name containing the other, which I do agree with you is a desirable effect that should be preserved. As I described, my approach inverts their relationship, so that it is the "integer uniform map" which is a specific type of "uniform map", rather than the other way around, where a "generalized patent val" is a generalized type of "patent val". In fact, when Dave Keenan and I were developing these proposals, it turned into somewhat of a drag-out fight, where for days I refused to budge that "integer uniform map" should be the only replacement for "patent val", while he only accepted "simple map", but we eventually came to the agreement that both terms had merit in different contexts. They are just two different helpful ways of thinking about the same structure; in contexts pertaining to tuning accuracy, "simple map" works great, and in contexts pertaining to other uniform maps, "integer uniform map" works great. --Cmloegcmluin (talk) 01:59, 28 September 2021 (UTC)

"Uniform" isn't very self-explanatory, IMO. I propose replacing GPV with "exact edomapping" or possibly non-integral or decimal edomapping. But in practice the GPV gets rounded off anyway, and none of these terms apply, not even uniform. In fact I must admit I'm confused what precisely a GPV is. I would think it's an exact, non-integral edomapping, and rounding it off turns it into a normal (i.e. integral) edomapping. But the article says "We can show that ⟨17 27 40] is a generalized patent val".

I think the whole concept of GPV would be much clearer if 1) GPV means only an exact un-rounded-off edomapping, and 2) there is a separate term for an integral edomapping that can result from rounding off a GPV. I propose "proper edomapping", which includes 17 and 17c and even 17bbccc (the ⟨17 28 41] of the article) but not 17cc or 17ccc. This seems to be the whole point of GPVs, to create a rigorous definition of proper and improper edomappings.

I'd also like to note that "exact edomapping" makes sense but "exact map" or "exact mapping" doesn't. Because there's no point in generalizing the meantone mapping [⟨1 0 -4], ⟨0 1 4]]. Point being, there are times when one wants to say edomapping not mapping (see my comment in the "simple map" discussion above). --TallKite (talk) 08:09, 28 September 2021 (UTC)

I agree that "uniform" is not self-explanatory. But I don't think self-explanatory-ness should be a target for terminology. I think it's only necessary that terms are descriptive. I think "generalized patent val" is also not self-explanatory, so it's not a relative point against "uniform map".

Unfortunately, I'm having trouble figuring out how best to reply to the rest of your thoughts and suggestions here. As you admit, you feel confused about what precisely this concept is, and it seems likely to me that you do have some misconception about it, because I can't follow much of your thinking, or reconcile many of your statements with my understanding of the ideas here. So perhaps we should both pause making suggestions or criticisms involving terminology, and first make sure that we're all on the same page about the structure itself.

I love visual explanations myself and hope that this one will be helpful to you, too. Uniform maps (or GPVs) finally clicked for me when a guy on the Discord server named Dead Shaman shared a special type of chart with me. I adapted his chart for use in my RTT How-To, where I explain that a uniform map is any map that can be found at a vertical line drawn through it. Here's an example (there's a lot of other stuff going on in these charts that's not necessary, so no need to understand everything):

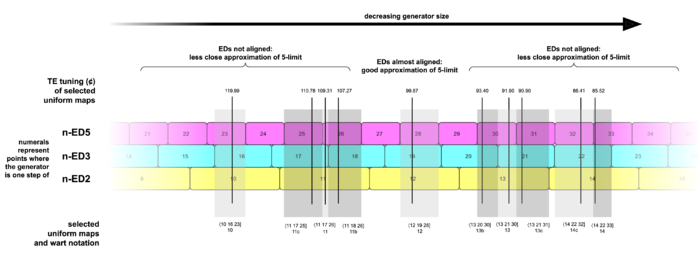
And that is why the example you were surprised about, ⟨17 27 40], is indeed a uniform map, because you can see it drawn as such a vertical line in another area of that chart, as seen here:

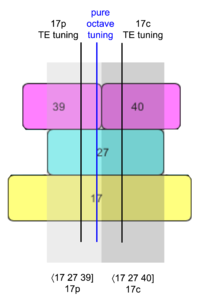
Please let me know if this explanation helps, or if you have any other questions. FloraC and I have also provided alternative explanations of the concept in our discussion above that aren't present in the article itself (yet... maybe we'll rework it soon), so if you are unfamiliar with those explanations, they may prove helpful as well. --Cmloegcmluin (talk) 16:48, 28 September 2021 (UTC)

I understand the math perfectly well. I understand the diagram too. What I don't understand is the terminology. Generalized in this context means generalized from integers to real numbers, right? Which allows the numbers to be exact, e.g. 3/1 is exactly 26.944/17 the size of 2/1, hence ⟨17 26.944] is an exact edomapping. And exact is what you mean by uniform, right? But nobody actually uses these real-number edomappings. Instead, the real numbers are rounded to integers. Which makes them not generalized, and not exact. So I don't understand, or more bluntly I strongly object to, calling the rounded edomappings generalized.

In other words, here's three of what I would call generalized PVs: ⟨17 26.944 39.473 47.725] and ⟨17.1 27.103 39.705 48.006] and ⟨17.45 27.658 40.518 48.988]. And here's what you get when you round them: ⟨17 27 39 48] and ⟨17 27 40 48] and ⟨17 28 41 49]. But there's nothing generalized about those last three. They are ordinary edomappings. But the whole point of exact real-number edomappings is that you can derive ordinary inexact integral edomappings from them. And because these three have been derived this way, they are more "reasonable" or "natural" than others which can't be. And "proper" is a much better term for that than "generalized". So IMO any edomapping through which you can draw a vertical line on the diagram and hit every component rectangle should be called a proper edomapping, and any one that you can't do this with should be called an improper edomapping.

Using my proposed terminology, 17edo has exactly 9 proper 7-limit edomappings, one of which is the nearest edomapping. As you would expect, the nearest edomapping of any edo is always proper. Using the current terminology, 17edo has 9 GPVs. One of them is the patent val, plus there's 8 non-patent vals. But each of those non-patent val is also a generalized patent val. So even though they're non-patent, they still have "patent" in the name. Which is confusing. This confusion goes away when you use the term proper.

Interesting side point: 17edo's smallest (i.e. contains the smallest numbers) proper edomapping is ⟨17 26 38 46]. And 16edo's largest is ⟨16 26 38 46]. The last 3 numbers are the same because 16.5 can be rounded up to 17 or down to 16. In other words, 16.5-edo is both stretched 17edo and compressed 16edo. In fact the whole section on GPVs might be improved by explicitly discussing stretched edos. We could even call GPVs stretched edomappings, if we use the word stretched loosely to mean both stretched and compressed and also neither one. Then what I'm calling proper edomappings would be called nearest stretched edomappings. --TallKite (talk) 08:40, 29 September 2021 (UTC)

Ah! Sorry. I did not mean to insult your intelligence or otherwise offend. As soon as I saw your reply, I remembered that when I drafted my previous post, I had the flicker of a thought that I should say something like "or maybe you do totally understand the concept but I just need you to clarify what you mean by 'exact' and 'proper'". I regret failing to follow through on that now. And you've gone ahead and done it for me. Thank you for that. Your full explanation lets me see that we're actually just about on the same page, so that's great.

To be clear, I am the one who made the original post here arguing against the terminology "generalized patent val". You don't have to convince me that it's bad; we agree on that. I do think FloraC here still supports it to some extent, so arguments presented against it are still useful. I myself have elsewhere made the point you make above about how putting the words "generalized" and "patent" together is already confusing; I see that I didn't make it myself above in my original post, so I'd like to explicitly say that I second that point.

You are correct so far when you say that the "generalized" part of "generalized patent val" means "from integers to reals". (And I'll take this opportunity to reiterate my position that it's more logical to structure it the other way around: defining a basic concept for the reals, i.e. uniform maps, and then specify integers when appropriate, i.e. integer uniform maps, AKA simple maps / patent vals / nearest edomappings.)

However, I think you have the wrong idea about which numbers exactly that "generalized patent vals" are supposed to be thought of as generalizing from integers from reals. So, to be clear, I am choosing to assist my opponents here by clarifying their reasoning, but of course I want us to have a fair consideration of each other's ideas at their best and clearest. And as far as I can tell, it seems to be the case that you think "generalized patent vals" generalize all of the entries in the map from integers to reals, but that is not correct. Only the EDO number that is used in the otherwise identical process for computing a patent val is generalized. Or as I prefer to think about it, what is generalized is the multiplier that the terms of the JIP (i.e. ⟨log₂2 log₂3 log₂5 ...]) are uniformly scaled by (except, again, I prefer to say that the default case is that this uniform multiplier is real, and if you need it to be integer, you say so).

You say that "nobody actually uses these real-number edomappings (directly)" and I agree with that. That's a big reason why structures like ⟨17 26.944 39.473 47.72], ⟨17.1 27.103 39.705 48.006], ⟨17.45 27.658 40.518 48.988] are not what we've given the name "generalized patent val"/"uniform map" for. You say that those are the structures that the name "generalized patent vals" makes sense for, and while I agree that generalized patent val could be a reasonable name for them if anyone wanted to name them, I don't believe there's a wide desire or any good reason to name these such structures at all. They don't have enough value in and of themselves. They are merely intermediate states before being rounded to the structures of value that are worth being named, i.e. "generalized patent vals"/"uniform maps" (I had to check your numbers here to make sure I understood what points you were illustrating with them — and yes, these are all indeed valid uniform scalings of the JIP which upon rounding would therefore give you GPVs/uniform maps).

Consider the case of a non-generalized patent val, or as I would say, an integer uniform map. What is the "integer" of the name here is the EDO or uniform scalar; note that other than the first term of the map pre-rounding, all of the other numbers in the map will always be reals, even for integer uniform maps / patent vals. Let's compare using the examples you gave yourself. ⟨17 26.944 39.473 47.72] rounds to ⟨17 27 39 48] and so that is the "patent val"/"(integer) uniform map" for 17, and ⟨17.1 27.103 39.705 48.006] rounds to ⟨17 27 40 48] and it is the "generalized patent val"/"uniform map" for 17.1. In both cases, all the entries in the final maps are integers. And in both cases, all of the entries in the not-yet-rounded maps besides the entry for prime 2 are reals. The only difference is whether the entry for prime 2 in the map before it is rounded is an integer or a real. Does it make sense now why "generalized patent val" is a reasonable term, and I why I'd disagree with you that there is "nothing generalized" about the final results? (Though again, I am defending our opponents' reasoning here; I think generalized patent val is reasonable, sure, but that's hardly enough for it to qualify as good or great at its job... just look how much confusion it has caused here alraedy, and how much work we're having to do in order to get on the same page about it!)

So the act of generalizing from integers to reals is not what "allows" things be exact, as you say. I can see now that you are using the word "exact maps" to name those not-yet-rounded maps such as ⟨17 26.944 39.473 47.72], ⟨17.1 27.103 39.705 48.006], ⟨17.45 27.658 40.518 48.988] which I suggested above don't need to be named. So, no, this is not what I mean by "uniform". My term "uniform map" is completely synonymous with "generalized patent val", which is the name for maps like these after they have been rounded. As you put it, "the whole point of exact real-number edomappings is that you can derive ordinary inexact integral edomappings from them". Right. I agree. If I had to rewrite that statement myself I would write "the point of maps that are uniform scalings of the JIP is that you can derive uniform maps from them".

You then say 'And because these three have been derived this way, they are more "reasonable" or "natural" than others which can't be. And "proper" is a much better term for that than "generalized".' I agree with all of your points here, and I now see what you mean by proper. But I think my proposed "uniform" is an even better term than "proper". That's because "uniform" is more descriptive. "Proper" is vague. When you used the word "proper" I had no idea what you meant. "Propriety" always requires further explanation about what qualities a thing is proper with respect to, while "uniformity" already gives you a sense of what the thing looks/feels/sounds like; uniform gives you the image of a perfectly straight vertical line drawn across the charts that I shared in my previous post, i.e. perfectly straight and not curved or wiggly or anything, which would be "unnatural" mapping choices. This is the same type of reasoning, actually, why FloraC above convinced me that your term "nearest" was superior to my term "simple" as a replacement for "patent"!

As you say, "Using my proposed terminology, 17edo has exactly 9 proper 7-limit edomappings, one of which is the nearest edomapping. As you would expect, the nearest edomapping of any edo is always proper." Using my proposed terminology, then, 17edo has exactly 9 uniform 7-limit maps, one of which is the integer uniform map AKA the nearest map. I think my terminology is slightly more self-explanatory than yours.

It looks like you're using the word "stretched" in the same sense as I'm using "scaled" in my explanations of "uniform", i.e. uniform scaling of the JIP before rounding. My word "scaled" supports both stretching and compressing already, so perhaps you would like to use it. But I don't think we should discuss "nearest stretched edomappings" until we've tied up some discussion points we've already got open. --Cmloegcmluin (talk) 17:19, 29 September 2021 (UTC)

OK, I understand now that ⟨17.1 27.103 39.705 48.006] is not a GPV. True, "proper" does need explanation. But it does seem appropriate for this. Hmm, still don't quite get the logic behind the term uniform, which the dictionary says means "identical or consistent, as from example to example" or "without variations in detail".

I do like "scaled", thank you I will use it! I'm good with "nearest scaled edomappings". The phrase is admittedly a bit intimidating, but I could see it working. The newcomer should first learn about edomappings, then nearest edomappings, then scaled edomappings, then nearest scaled edomappings. We could call them NSEs or something, unless we call them proper/uniform. --TallKite (talk) 00:47, 30 September 2021 (UTC)

I'm glad we're on the same page now re: GPVs. I agree "proper" is a reasonable choice. I probably like it better than "generalized". But I still prefer "uniform". Of course, the fact that I need to provide extra explanation for "uniform" to you doesn't bode well for my case :) But let me give it a shot, leaning on the dictionary definition you provided. Please glance back up at my charts I pasted above. Again, the perfectly straight vertical lines I draw through the chart represent uniform maps. I suppose you could think of these lines, as you follow them vertically through the chart, as "choosing" the mapping for each prime. The fact that I require the line to be perfectly straight up-and-down is what makes it work. So if I had not uniformly scaled the lines per each of the primes, the line wouldn't be perfectly straight, and I wouldn't have a uniform map. That's the uniform part: uniform per prime, no variations in scale between them, identical and consistent scaling per prime. Does that work? As I explain it, I'm realizing that "straight map" might work just as well or better. What are your thoughts on that?

I'm glad you like "scaled". But I still prefer uniform map. I don't know what you mean by a "scaled edomapping" (one that's not a "nearest scaled edomapping"... what is scaled of, then?). In my opinion a newcomer would first learn about maps, then uniform maps, then integer uniform maps. That's the order I present the ideas in my RTT How-To at present. --Cmloegcmluin (talk) 01:36, 30 September 2021 (UTC)