Oneirotonic
The term oneirotonic (/oʊnaɪrəˈtɒnɪk/ oh-ny-rə-TON-ik or /ənaɪrə-/ ə-ny-rə-) is used for the 8-note MOS structure 5L 3s, whose brightest mode is LLsLLsLs. The name "oneirotonic" was coined by Cryptic Ruse after the Dreamlands in H.P. Lovecraft's Dream Cycle mythos. Oneirotonic is a distorted diatonic, because it has one extra small step compared to diatonic (5L 2s).
The generator size ranges from 450¢ (3\8) to 480¢ (2\5). Hence any edo with an interval between 450¢ and 480¢ has an oneirotonic scale.
In terms of regular temperaments, there are at least two melodically viable ways to interpret oneirotonic:
- When the generator is between 461.54¢ (5\13) and 466.67¢ (7\18): A-Team (13&18, a 4:5:9:21 or 2.9.5.21 temperament)
- When the generator is between 457.14¢ (8\21) and 461.54¢ (5\13): Petrtri (13&21, a 4:5:9:11:13:17 or 2.5.9.11.13.17 temperament)
Notation
The notation used in this article is LLsLLsLs = JKLMNOPQJ (with J ≈ 180 Hz), unless specified otherwise.
Intervals
| Generators | Notation (1/1 = J) | Octatonic interval category name | Generators | Notation of 2/1 inverse | Octatonic interval category name |
|---|---|---|---|---|---|
| The "diatonic" 8-note scale has the following intervals (from some root): | |||||
| 0 | J | perfect unison | 0 | J | octave |
| 1 | M | perfect mosfourth | -1 | Ob | perfect mossixth |
| 2 | P | major mosseventh | -2 | Lb | minor mosthird |
| 3 | K | major mossecond | -3 | Qb | minor moseighth |
| 4 | N | major mosfifth | -4 | Nb | minor mosfifth |
| 5 | Q | major moseighth | -5 | Kb | minor mossecond |
| 6 | L | major mosthird | -6 | Pb | minor mosseventh |
| 7 | O | augmented sixth | -7 | Mb | diminished fourth |
| The "chromatic" 13-note scale also has the following intervals (from some root): | |||||
| 8 | J# | augmented unison | -8 | Jb | diminished octave |
| 9 | M# | augmented mosfourth | -9 | Obb | diminished mossixth |
| 10 | P# | augmented mosseventh | -10 | Lbb | diminished mosthird |
| 11 | K# | augmented mossecond | -11 | Qbb | diminished moseighth |
| 12 | N# | augmented mosfifth | -12 | Nbb | diminished mosfifth |
Modal harmony
Oneirotonic modes are named after cities in the Dreamlands.
- Dylathian: LLsLLsLs (major with hints of Mixolydian and "#5")
- Ilarnekian: LLsLsLLs (major with hints of "b6")
- Celephaïsian: LsLLsLLs (the oneirotonic melodic minor. Very classical-sounding; Easley Blackwood's 13-note etude uses this as its home mode.)
- Ultharian: LsLLsLsL (A Dorian analogue. Another Dorian analogue is the MODMOS LsLLLsLs)
- Mnarian: LsLsLLsL
- Kadathian: sLLsLLsL (another "Locrian")
- Hlanithian: sLLsLsLL (closest Locrian analogue)
- Sarnathian: sLsLLsLL (Darkest but ironically the most consonant. Here be dragons.)
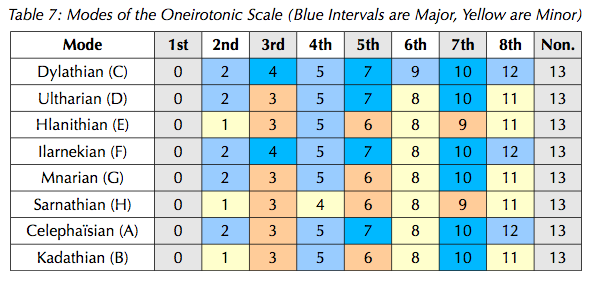
The modes in 13edo edo steps and C-H notation:
Modes with sharp tritone
At least in A-Team, the brighter modes can be viewed as providing a distorted version of diatonic functional harmony. For example, in the Dylathian mode, the 4:5:9 triad on the sixth degree can sound like both "V" and "III of iv" depending on context. Basic chord progressions can move by minor fourths, thirds, or major seconds: for example, J major-M minor-P minor-Ob major-J major (in Ilarnekian) or J major-K major-O major-M major-J major (in Dylathian).
Modes with flat tritone
The darker modes are radically different in character than the brighter modes. Because of the consonant 11/8 minor tritone and the 13/8 minor sixth, the flat tritone sounds more like a stable scale function.
A-Team (13&18, 4:5:9:(11:13):21) interpretation
The sizes of the generator, large step and small step of oneirotonic are as follows in various edos:
| 13edo | 18edo | 31edo | 64/49 generator | JI intervals represented (2.9.5.21 subgroup) | |
|---|---|---|---|---|---|
| generator | 5\13, 461.54 | 7\18, 466.67 | 12\31, 464.52 | 462.35 | 21/16 |
| L | 2\13, 184.62 | 3\18, 200.00 | 5\31, 193.55 | 187.04 | 9/8, 10/9 |
| s | 1\13, 92.31 | 1\18, 66.66 | 2\31, 77.42 | 88.26 | 21/20 |
Intervals
Sortable table of Dylathian, the brightest mode:
| Degree | Size in 13edo | Size in 18edo | Size in 31edo | Note name on J | Approximate ratios[1] | #Gens up |
|---|---|---|---|---|---|---|
| 1 | 0\13, 0.00 | 0\18, 0.00 | 0\31, 0.00 | J | 1/1 | 0 |
| 2 | 2\13, 184.62 | 3\18, 200.00 | 5\31, 193.55 | K | 9/8, 10/9 | +3 |
| 3 | 4\13, 369.23 | 6\18, 400.00 | 10\31, 387.10 | L | 5/4 | +6 |
| 4 | 5\13, 461.54 | 7\18, 466.67 | 12\31, 464.52 | M | 21/16, 13/10 | +1 |
| 5 | 7\13, 646.15 | 10\18, 666.66 | 17\31, 658.06 | N | 13/9, 16/11 | +4 |
| 6 | 9\13, 830.77 | 13\18, 866.66 | 22\31, 851.61 | O | 13/8, 18/11 | +7 |
| 7 | 10\13, 923.08 | 14\18, 933.33 | 24\31, 929.03 | P | 12/7 | +2 |
| 8 | 12\13, 1107.69 | 17\18, 1133.33 | 29\31, 1122.58 | Q | +5 |
- ↑ The harmonics over 1/1 are in bold. The ratio interpretations that are not valid for 18edo are italicized.
Chords
Despite being melodically familiar, oneirotonic is harmonically complex in that it doesn't represent many lower-complexity JI triads other than 4:9:21, 9:10:13, and the occasional 4:5:9. Hence oneirotonic may especially benefit from either using inharmonic timbres in addition to harmonic ones or using a well-tempered version of 13edo adopted for this scale. The availability of certain consonances also varies greatly by mode: for example, only Dylathian, Ilarnekian and Sarnathian have a 5/4 on the tonic, and only Mnarian, Kadathian, Hlanithian and Sarnathian have an 11/8 on the tonic.
Petrtri (13&21, 4:5:9:11:13:17) interpretation
The sizes of the generator, large step and small step of oneirotonic are as follows in various tunings. (Golden oneirotonic uses 1200*(2-φ) = 458.3592135¢ as generator and has L/s = φ; it is the limit of Fibonacci number edos 13, 21, 34, 55, 89,... in oneirotonic tunings.)
| 13edo | 21edo | 34edo | Golden oneirotonic | JI intervals represented (2.5.9.11.13.17 subgroup) | |
|---|---|---|---|---|---|
| generator | 5\13, 461.54 | 8\21, 457.14 | 13\34, 458.82 | 458.36 | 13/10, 17/13, 22/17 |
| L | 2\13, 184.62 | 3\21, 171.43 | 5\34, 176.47 | 175.08 | 10/9, 11/10 |
| s | 1\13, 92.31 | 2\21, 114.29 | 3\34, 105.88 | 108.20 | 18/17, 17/16 |
Intervals
Sortable table of Dylathian, the brightest mode:
| Degree | Size in 13edo | Size in 21edo | Size in 34edo | Note name on J | Approximate ratios | #Gens up |
|---|---|---|---|---|---|---|
| 1 | 0\13, 0.00 | 0\21, 0.00 | 0\34, 0.00 | J | 1/1 | 0 |
| 2 | 2\13, 184.62 | 3\21, 171.43 | 5\34, 176.47 | K | 10/9, 11/10 | +3 |
| 3 | 4\13, 369.23 | 6\21, 342.86 | 10\34, 352.94 | L | 11/9, 16/13 | +6 |
| 4 | 5\13, 461.54 | 8\21, 457.14 | 13\34, 458.82 | M | 13/10, 17/13, 22/17 | +1 |
| 5 | 7\13, 646.15 | 11\21, 628.57 | 18\34, 635.294 | N | 13/9, 16/11 | +4 |
| 6 | 9\13, 830.77 | 14\21, 800.00 | 23\34, 811.77 | O | 8/5 | +7 |
| 7 | 10\13, 923.08 | 16\21, 914.29 | 26\34, 917.65 | P | 17/10 | +2 |
| 8 | 12\13, 1107.69 | 19\21, 1085.71 | 31\34, 1094.12 | Q | 17/9, 32/17 | +5 |
Chords
The pentad P1-m8-M10-m12-M16 "5:9:11:13:17" occurs twice in the 8 note mos of 13edo and 21edo's father[8]. The pentad P1-M3-M4-m6-m9 "4:5:11:13:17" occurs once.
Triad occurrences:
- P1-M2-M3 "9:10:11" occurs 2x
- P1-M2-M5 "9:10:13" occurs 3x
- P1-M2-M8 "9:10:17" occurs 3x
- P1-M3-M5 "9:11:13" occurs 2x
- P1-M3-M8 "9:11:17" occurs 2x
- P1-M5-M8 "9:13:17" occurs 3x
All 8 modes provide chords in various prime families (list of modes is non-exhaustive):
- /2 chords occur on Sarnathian
- /5 chords occur on Ultharian and Mnarian
- /9 chords occur on Dylathian and Ilarnekian
- /11 chords occur on Hlanithian and Sarnathian
- /13 chords occur on Mnarian and Kadathian
- /17 chords occur on Hlanithian and Kadathian
Samples
(A rather classical-sounding 3-part harmonization of the ascending J Ilarnekian scale; tuning is 13edo)
(13edo, first 30 seconds is in Celephaïsian mode)
(13edo, Ilarnekian)
(by Igliashon Jones, 13edo)