AFDO

From Xenharmonic Wiki
Revision as of 18:34, 30 March 2023 by Cmloegcmluin (talk | contribs) (add history and revise page to reflect it, clarify terminological relationships)
Jump to navigation Jump to search

An ADO (arithmetic divisions of the octave) is a periodic tuning system which divides the octave according to an arithmetic progression of frequency.

For example, in 12ado the first degree is 13/12, the second is 14/12 (7/6), and so on. For an ADO system, the difference between interval ratios is equal (they form an arithmetic progression), rather than their ratios between interval ratios being equal as in EDO systems (a geometric progression). All ADOs are subsets of just intonation. ADOs with more divisors such as highly composite ADOs generally have more useful just intervals.

When treated as a scale, the ado is equivalent to the overtone scale. An ADO is equivalent to an ODO (otonal division of the octave). It may also be called an EFDO (equal frequency division of the octave), however, this more general acronym is typically reserved for divisions of irrational intervals, unlike the octave.

Formula

Within each period of any n-ado system, the frequency ratio r of the m-th degree is

[math]\displaystyle{ \displaystyle r = (n + m)/n }[/math]

If the first division is r0 (which is ratio of (n + 0)/n = 1) and the last, rn (which is ratio of (n + n)/n = 2), with common difference of d (which is 1/n), we have:

[math]\displaystyle{ r_1 = r_0 + d \\ r_2 = r_0 + 2d \\ r_3 = r_0 + 3d \\ \vdots \\ r_m = r_0 + md }[/math]

Relation to string lengths

If the first division has ratio of r1 and length of l1 and the last, rn and Ln , we have: ln = 1/rn and if rn > … > r3 > r2 > r1, then l1 > l2 > l3 > … > ln

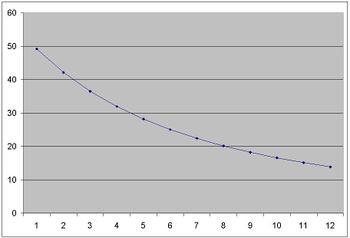
These lengths are related to the inverse of ratios in the system. The above picture shows the differences between divisions of length in 12ado system. On the contrary, we have equal divisions of length in EDL systems (→ EDL system):

Relation to superparticular ratios

An ADO has step sizes of superparticular ratios with increasing numerators. For example, 5ado has step sizes of 6/5, 7/6, 8/7, and 9/8.

Relation to otonality & harmonic series

We can consider ADO system as an otonal system. Otonality is a term introduced by Harry Partch to describe chords whose notes are the overtones (multiples) of a given fixed tone. Considering ADO, an otonality is a collection of pitches which can be expressed in ratios that have equal denominators. For example, 1/1, 5/4, and 3/2 form an otonality because they can be written as 4/4, 5/4, 6/4. Every otonality is therefore part of the harmonic series. An otonality corresponds to an arithmetic series of frequencies or a harmonic series of wavelengths or distances on a string instrument.

History

The term ADO was proposed by Shaahin Mohajeri in 2006, along with the term EDL (equal division of length)[1]. Previously, scales/tunings equivalent to n-ADO's had been known as "mode n of the harmonic series", "over-n scales", and n-EDL's had been known as "aliquot-n" scales. Neither of Shaahin's two new concepts were systematic extensions of the term EDO (equal division of the octave), and no one else used these two terms besides Shaahin himself. In 2021, a team consisting of Douglas Blumeyer, Billy Stiltner, and Paul Erlich developed the first systematic extension of EDO from equal divisions of pitch to equal divisions of frequency and length, including special terms for divisions of rational intervals such as the octave; under this system, an n-ADO would be an n-ODO. In 2023, Flora Canou revived the term ADO by leveraging the ambiguity in the word "arithmetic", repurposing it as a reference to the arithmetic mean rather than to arithmetic progressions, then extended this interpretation to the term IDO, for "inverse-arithmetic division of the octave" by coining "inverse-harmonic mean".

Individual pages for ADOs

See also

  1. ↑ https://yahootuninggroupsultimatebackup.github.io/makemicromusic/topicId_13427.html#13427
Retrieved from "https://en.xen.wiki/index.php?title=AFDO&oldid=106370"