Gravity
| Gravity; larry |
243/242, 4000/3993 (2.3.5.11)
((2.3.5.11) 15-odd limit) ? ¢
((2.3.5.11) 15-odd limit) 51 notes
Gravity is a rank-2 temperament and parent of the gravity family, generated by a classical grave fifth (40/27), six of which stacked reach the interval class of 4/3, and thereby characterized by the vanishing of the graviton (ratio: 129140163/128000000, monzo: [-13 17 -6⟩).
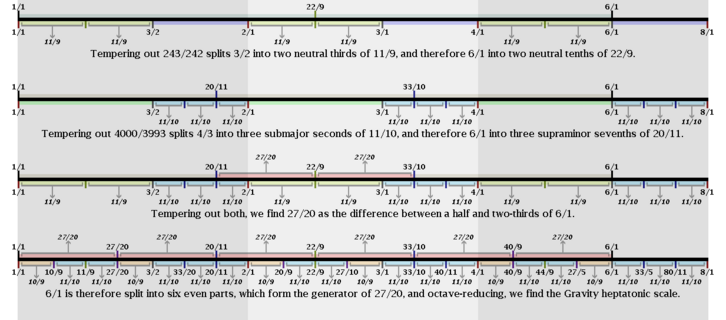
Gravity is most naturally seen as a 2.3.5.11 subgroup temperament, sometimes known as larry. Here S9/S10 = 8019/8000 is tempered out, so that two intervals of 40/27 reach 11/10, and S10/S11 = 4000/3993 is tempered out, so that three intervals of 11/10 reach 4/3; these equivalences also imply that 243/242 is tempered out; three 27/20 fourths reach 11/9, which is equated to 27/22 and acts as an exact neutral third. Gravity's generator lies close to the fifth of 7edo, implying that the MOS scales of gravity cluster heavily around 7edo, and in this interpretation the comma reached after 7 generators simultaneously represents S9 = 81/80, S10 = 100/99, and S11 = 121/120.
Strong extensions with prime 7 include gravid (58 & 65), 58 & 65d, marvo (65d & 72), and zarvo (65 & 72). However, the most notable extension of gravity is harry (58 & 72), which splits the octave in two and extends well to the 13- and 17-limit.
For technical data, see Gravity family #Gravity.
A pictorial representation of the process of constructing the heptatonic MOS of 2.3.5.11 gravity. Splitting 3/2 in two and splitting 4/3 in three are equivalent to splitting 6/1 in six, and Gravity[7] is equivalent to the scale obtained by octave-reducing 6ed6.
Intervals
Interval chain
In the following table, odd harmonics 1–15 are labeled in bold.
| # | Cents* | Approximate ratios |
|---|---|---|
| 0 | 0.0 | 1/1 |
| 1 | 516.8 | 27/20, 121/90 |
| 2 | 1033.7 | 20/11 |
| 3 | 350.5 | 11/9, 27/22 |
| 4 | 867.4 | 33/20, 200/121 |
| 5 | 184.2 | 10/9, 135/121 |
| 6 | 701.1 | 3/2 |
| 7 | 17.9 | 81/80, 100/99, 121/120 |
| 8 | 534.8 | 15/11, 110/81 |
| 9 | 1051.6 | 11/6, 81/44 |
| 10 | 368.5 | 99/80, 100/81, 150/121 |
| 11 | 885.3 | 5/3 |
| 12 | 202.2 | 9/8, 121/108 |
| 13 | 719.0 | 50/33, 121/80 |
| 14 | 35.9 | 45/44, 55/54 |
| 15 | 552.7 | 11/8 |
| 16 | 1069.6 | 50/27 |
| 17 | 386.4 | 5/4 |
| 18 | 903.3 | 27/16, 121/72 |
| 19 | 220.1 | 25/22 |
| 20 | 737.0 | 55/36 |
| 21 | 53.8 | 33/32, 125/121 |
| 22 | 570.7 | 25/18 |
| 23 | 1087.5 | 15/8 |
* In 2.3.5.11-subgroup CTE tuning
As a detempering of 7et
|
Todo: add detempering info |
Tunings
|
|
Todo: add tuning spectrum |