137edo: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
m cleanup, simplify |
||
| Line 1: | Line 1: | ||
{{Infobox ET}} | {{Infobox ET}} | ||
The ''137 equal division'' divides the octave into 137 equal parts of 8.759 cents each. It is the [[ | The '''137 equal division''' divides the octave into 137 equal parts of 8.759 cents each. It is the [[optimal patent val]] for 7-limit [[orwell]] temperament and for the planar temperament tempering out 2430/2401. It tempers out 2109375/2097152 (the semicomma) in the 5-limit; 225/224 and 1728/1715 in the 7-limit; 243/242 in the 11-limit; 351/350 in the 13-limit; 375/374 and 442/441 in the 17-limit; and 324/323 and 495/494 in the 19-limit. Since it is the 33rd [[prime number]], 137edo has no proper divisors aside from 1. | ||
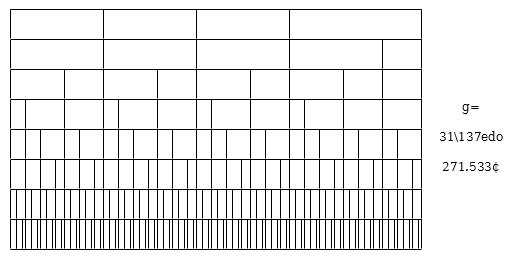
A diagram of 7-limit Orwell based on the 31\137edo generator: | A diagram of 7-limit Orwell based on the 31\137edo generator: | ||
Revision as of 12:48, 27 November 2022
| ← 136edo | 137edo | 138edo → |
The 137 equal division divides the octave into 137 equal parts of 8.759 cents each. It is the optimal patent val for 7-limit orwell temperament and for the planar temperament tempering out 2430/2401. It tempers out 2109375/2097152 (the semicomma) in the 5-limit; 225/224 and 1728/1715 in the 7-limit; 243/242 in the 11-limit; 351/350 in the 13-limit; 375/374 and 442/441 in the 17-limit; and 324/323 and 495/494 in the 19-limit. Since it is the 33rd prime number, 137edo has no proper divisors aside from 1.
A diagram of 7-limit Orwell based on the 31\137edo generator: