Limmic temperaments: Difference between revisions
m Removing from Category:Regular temperament theory using Cat-a-lot |
Update keys and improve description for blackweed |
||
| Line 3: | Line 3: | ||
== Blacksmith == | == Blacksmith == | ||
=== 5-limit (blackwood) === | === 5-limit (blackwood) === | ||
Subgroup: 2.3.5 | [[Subgroup]]: 2.3.5 | ||
[[Comma list]]: 256/243 | [[Comma list]]: 256/243 | ||
| Line 11: | Line 11: | ||
Mapping generators: ~9/8, ~5 | Mapping generators: ~9/8, ~5 | ||
[[POTE | [[Optimal tuning]] ([[POTE]]): ~9/8 = 1\5, ~5/4 = 399.594 | ||
{{Val list|legend=1| 5, 10, 15 }} | {{Val list|legend=1| 5, 10, 15 }} | ||
| Line 20: | Line 20: | ||
[[File:blacksmith10.jpg|alt=blacksmith10.jpg|thumb|Lattice of blacksmith]] | [[File:blacksmith10.jpg|alt=blacksmith10.jpg|thumb|Lattice of blacksmith]] | ||
Subgroup: 2.3.5.7 | [[Subgroup]]: 2.3.5.7 | ||
[[Comma list]]: 28/27, 49/48 | [[Comma list]]: 28/27, 49/48 | ||
| Line 30: | Line 30: | ||
{{Multival|legend=1| 0 5 0 8 0 -14 }} | {{Multival|legend=1| 0 5 0 8 0 -14 }} | ||
[[POTE | [[Optimal tuning]] ([[POTE]]): ~9/8 = 1\5, ~5/4 = 392.767 | ||
{{Val list|legend=1| 5, 10, 15, 40b, 55b }} | {{Val list|legend=1| 5, 10, 15, 40b, 55b }} | ||
| Line 43: | Line 43: | ||
Mapping: [{{val| 5 8 0 14 29 }}, {{val| 0 0 1 0 -1 }}] | Mapping: [{{val| 5 8 0 14 29 }}, {{val| 0 0 1 0 -1 }}] | ||
POTE | Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 394.948 | ||
Optimal GPV sequence: {{Val list| 5, 10, 15, 40be, 55be, 70bde, 85bcde }} | Optimal GPV sequence: {{Val list| 5, 10, 15, 40be, 55be, 70bde, 85bcde }} | ||
| Line 56: | Line 56: | ||
Mapping: [{{val| 5 8 0 14 29 7 }}, {{val| 0 0 1 0 -1 1 }}] | Mapping: [{{val| 5 8 0 14 29 7 }}, {{val| 0 0 1 0 -1 1 }}] | ||
POTE | Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 391.037 | ||
Optimal GPV sequence: {{Val list| 5, 10, 15, 25e, 40bef }} | Optimal GPV sequence: {{Val list| 5, 10, 15, 25e, 40bef }} | ||
| Line 69: | Line 69: | ||
Mapping: [{{val| 5 8 0 14 -6 }}, {{val| 0 0 1 0 2 }}] | Mapping: [{{val| 5 8 0 14 -6 }}, {{val| 0 0 1 0 2 }}] | ||
POTE | Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 398.070 | ||
Optimal GPV sequence: {{Val list| 5e, 10e, 15 }} | Optimal GPV sequence: {{Val list| 5e, 10e, 15 }} | ||
| Line 82: | Line 82: | ||
Mapping: [{{val| 5 8 0 14 -6 7 }}, {{val| 0 0 1 0 2 1 }}] | Mapping: [{{val| 5 8 0 14 -6 7 }}, {{val| 0 0 1 0 2 1 }}] | ||
POTE | Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 396.812 | ||
Optimal GPV sequence: {{Val list| 5e, 10e, 15 }} | Optimal GPV sequence: {{Val list| 5e, 10e, 15 }} | ||
| Line 95: | Line 95: | ||
Mapping: [{{val| 5 8 0 14 6 }}, {{val| 0 0 1 0 1 }}] | Mapping: [{{val| 5 8 0 14 6 }}, {{val| 0 0 1 0 1 }}] | ||
POTE | Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 374.763 | ||
Optimal GPV sequence: {{Val list| 5e, 10 }} | Optimal GPV sequence: {{Val list| 5e, 10 }} | ||
| Line 102: | Line 102: | ||
== Blackweed == | == Blackweed == | ||
Blackweed is | Blackweed is a variant of blackwood as it tempers out 256/243 alike but in the 2.3.11/7 [[subgroup]]. 20edo is close to the optimum, which has 4\20 as the period and 420¢ as the generator. | ||
Subgroup: 2.3.11/7 | [[Subgroup]]: 2.3.11/7 | ||
[[Comma list]]: 256/243 | [[Comma list]]: {{monzo| 8 -5 }} = 256/243 | ||
[[ | [[Sval]] [[mapping]]: [{{val| 5 8 0 }}, {{val| 0 0 1 }}] | ||
Sval mapping generators: ~9/8, ~11/7 | |||
[[POTE | [[Optimal tuning]] ([[subgroup POTE]]): ~11/7 = 786.2215 | ||
{{Val list|legend=1| 15, 20, 35b }} | {{Val list|legend=1| 15, 20, 35b }} | ||
Revision as of 10:33, 21 December 2022
This limmic temperaments page collects various temperaments tempering out the Pythagorean limma, 256/243. As a consequence, 3/2 is always represented by 3\5, 720 cents assuming pure octaves. While quite sharp, this is close enough to a just fifth to serve as a fifth, and some people are fond of it.
Blacksmith
5-limit (blackwood)
Subgroup: 2.3.5
Comma list: 256/243
Mapping: [⟨5 8 0], ⟨0 0 1]]
Mapping generators: ~9/8, ~5
Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 399.594
Badness: 0.063760
7-limit
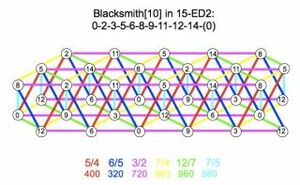
Subgroup: 2.3.5.7
Comma list: 28/27, 49/48
Mapping: [⟨5 8 0 14], ⟨0 0 1 0]]
Mapping generators: ~7/6, ~5
Wedgie: ⟨⟨ 0 5 0 8 0 -14 ]]
Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 392.767
Badness: 0.025640
11-limit
Subgroup: 2.3.5.7.11
Comma list: 28/27, 49/48, 55/54
Mapping: [⟨5 8 0 14 29], ⟨0 0 1 0 -1]]
Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 394.948
Optimal GPV sequence: Template:Val list
Badness: 0.024641
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 28/27, 40/39, 49/48, 55/54
Mapping: [⟨5 8 0 14 29 7], ⟨0 0 1 0 -1 1]]
Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 391.037
Optimal GPV sequence: Template:Val list
Badness: 0.020498
Farrier
Subgroup: 2.3.5.7.11
Comma list: 28/27, 49/48, 77/75
Mapping: [⟨5 8 0 14 -6], ⟨0 0 1 0 2]]
Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 398.070
Optimal GPV sequence: Template:Val list
Badness: 0.029200
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 28/27, 40/39, 49/48, 66/65
Mapping: [⟨5 8 0 14 -6 7], ⟨0 0 1 0 2 1]]
Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 396.812
Optimal GPV sequence: Template:Val list
Badness: 0.022325
Ferrum
Subgroup: 2.3.5.7.11
Comma list: 28/27, 35/33, 49/48
Mapping: [⟨5 8 0 14 6], ⟨0 0 1 0 1]]
Optimal tuning (POTE): ~9/8 = 1\5, ~5/4 = 374.763
Optimal GPV sequence: Template:Val list
Badness: 0.030883
Blackweed
Blackweed is a variant of blackwood as it tempers out 256/243 alike but in the 2.3.11/7 subgroup. 20edo is close to the optimum, which has 4\20 as the period and 420¢ as the generator.
Subgroup: 2.3.11/7
Comma list: [8 -5⟩ = 256/243
Sval mapping: [⟨5 8 0], ⟨0 0 1]]
Sval mapping generators: ~9/8, ~11/7
Optimal tuning (subgroup POTE): ~11/7 = 786.2215