AFDO

An ADO (arithmetic divisions of the octave) or EFDO (equal frequency division of the octave), also known as a chord of nature, is a periodic tuning system which divides the octave arithmetically rather than logarithmically.

For any C-ADO system, the m-th degree is equal to the ratio (C + m)/C. For example, in 12ado the first degree is 13/12, the second is 14/12 (7/6), and so on. For an ADO system, the distance between interval ratios is equal, rather than the distance between their logarithms like in EDO systems. All ADOs are subsets of just intonation. ADOs with more divisors such as highly composite ADOs generally have more useful just intervals.

If the first division is [math]\displaystyle{ R_1 }[/math] (which is ratio of C/C) and the last , [math]\displaystyle{ R_n }[/math] (which is ratio of 2C/C), with common difference of d

(which is 1/C), we have :

[math]\displaystyle{ R_2 = R_1 + d \\ R_3= R_1 + 2d \\ R_4 = R_1 + 3d \\ \vdots \\ R_n = R_1 + (n-1)d }[/math]

Relation to string lengths

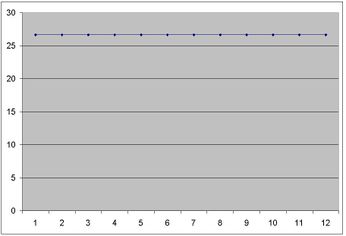
If the first division has ratio of r₁ and length of l₁ and the last, r_n and L_n , we have: l_n = 1/r_n and if r_n > … > r₃ > r₂ > r₁, then l₁ > l₂ > l₃ > … > l_n

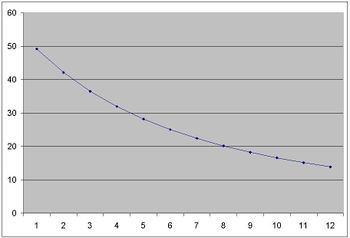
These lengths are related to the inverse of ratios in the system. The above picture shows the differences between divisions of length in 12ado system. On the contrary, we have equal divisions of length in EDL systems (→ EDL system):

Relation to superparticular ratios

An ADO has step sizes of superparticular ratios with increasing numerators. For example, 5ado has step sizes of 6/5, 7/6, 8/7, and 9/8.

Relation to otonality & harmonic series

We can consider ADO system as otonal system. Otonality is a term introduced by Harry Partch to describe chords whose notes are the overtones (multiples) of a given fixed tone.Considering ADO , an Otonality is a collection of pitches which can be expressed in ratios that have equal denominators. For example, 1/1, 5/4, and 3/2 form an otonality because they can be written as 4/4, 5/4, 6/4. Every Otonality is therefore part of the harmonic series. An otonality corresponds to an arithmetic series of frequencies or a harmonic series of wavelengths or distances on a string instrument.

Individual pages for ADOs

• 2ado
• 3ado
• 4ado
• 5ado
• 6ado
• 7ado
• 8ado
• 9ado
• 10ado
• 11ado
• 12ado
• 13ado
• 14ado
• 15ado
• 16ado
• 17ado
• 18ado
• 19ado
• 20ado
• 21ado
• 22ado
• 23ado
• 24ado
• 25ado
• 30ado
• 40ado
• 50ado
• 60ado
• 100ado
• 120ado

See also

• Arithmetic interval chain
• Arithmetic MOS scale
• Fret position calculator (excel sheet) based on EDL system and string length
• How to approximate EDO and ADO systems with each other? Download this file
• Magic of Tone and the Art of Music by the late Dane Rhudyar
• OD, or otonal division: An n-ADO is equivalent to an n-ODO.
• The nth overtone mode, or over-n scale is also equivalent to n-ADO.