137edo: Difference between revisions
Wikispaces>xenwolf **Imported revision 285903432 - Original comment: Reverted to Dec 14, 2011 2:20 pm: spam removed** |
ArrowHead294 (talk | contribs) mNo edit summary |
||
| (20 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
{{Infobox ET}} | |||
{{ED intro}} | |||
== Theory == | |||
137edo is a fairly accurate 5-limit temperament and also a strong no-7 19-limit temperament. The equal temperament [[tempering out|tempers out]] 2109375/2097152 ([[semicomma]]), {{monzo| -13 17 -6 }} ([[graviton]]), {{monzo| 8 14 -13 }} ([[parakleisma]]), and {{monzo| -29 -11 20 }} (gammic comma) in the 5-limit. Using the [[patent val]], it tempers out [[225/224]], [[1728/1715]], 2430/2401 in the 7-limit; [[243/242]] in the 11-limit; [[351/350]] in the 13-limit; [[375/374]] and [[442/441]] in the 17-limit; and [[324/323]] and [[495/494]] in the 19-limit. It provides the [[optimal patent val]] for 7-limit [[orwell]] temperament and for the planar temperament [[tempering out]] [[2430/2401]]. | |||
=== Prime harmonics === | |||
{{Harmonics in equal|137}} | |||
=== Subsets and supersets === | |||
137edo is the 33rd [[prime edo]], following [[131edo]] and before [[139edo]]. [[274edo]], which doubles it, provides a correction for its approximation to harmonic 7. | |||
== Regular temperament properties == | |||
{| class="wikitable center-4 center-5 center-6" | |||
|- | |||
! rowspan="2" | [[Subgroup]] | |||
! rowspan="2" | [[Comma list]] | |||
! rowspan="2" | [[Mapping]] | |||
! rowspan="2" | Optimal<br />8ve stretch (¢) | |||
! colspan="2" | Tuning error | |||
|- | |||
! [[TE error|Absolute]] (¢) | |||
! [[TE simple badness|Relative]] (%) | |||
|- | |||
| 2.3 | |||
| {{monzo| -217 137 }} | |||
| {{mapping| 137 217 }} | |||
| +0.3865 | |||
| 0.3866 | |||
| 4.41 | |||
|- | |||
| 2.3.5 | |||
| {{monzo| -21 3 7 }}, {{monzo| -13 17 -6 }} | |||
| {{mapping| 137 217 318 }} | |||
| +0.3887 | |||
| 0.3157 | |||
| 3.60 | |||
|} | |||
=== Rank-2 temperaments === | |||
{| class="wikitable center-all left-5" | |||
|+ style="font-size: 105%;" | Table of rank-2 temperaments by generator | |||
|- | |||
! Periods<br />per 8ve | |||
! Generator* | |||
! Cents* | |||
! Associated<br />ratio* | |||
! Temperaments | |||
|- | |||
| 1 | |||
| 3\137 | |||
| 26.28 | |||
| 1594323/1562500 | |||
| [[Sfourth]] (5-limit) | |||
|- | |||
| 1 | |||
| 4\137 | |||
| 35.04 | |||
| 1990656/1953125 | |||
| [[Gammic]] (137d) / [[gammy]] (137) | |||
|- | |||
| 1 | |||
| 31\137 | |||
| 271.53 | |||
| 75/64 | |||
| [[Orwell]] (137e) / [[sabric]] (137d) | |||
|- | |||
| 1 | |||
| 36\137 | |||
| 315.33 | |||
| 6/5 | |||
| [[Parakleismic]] | |||
|- | |||
| 1 | |||
| 53\137 | |||
| 464.23 | |||
| 72/55 | |||
| [[Borwell]] | |||
|- | |||
| 1 | |||
| 59\137 | |||
| 516.79 | |||
| 27/20 | |||
| [[Marvo]] (137) | |||
|- | |||
| 1 | |||
| 63\137 | |||
| 551.82 | |||
| 11/8 | |||
| [[Emka]] (137d) / [[emkay]] (137) | |||
|} | |||
<nowiki />* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if distinct | |||
== Diagrams == | |||
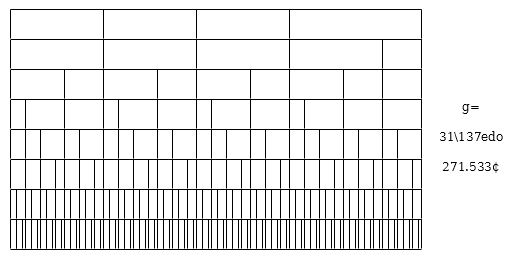
A diagram of 7-limit orwell based on the 31\137edo generator: | |||
[[File:137edo_MOS_031_demo_correction.png|alt=137edo_MOS_031_demo_correction.png|137edo_MOS_031_demo_correction.png]] | |||
[[:File:137edo_MOS_031.svg|137edo_MOS_031.svg]] | |||
[[Category:Nuwell]] | |||
[[Category:Orwell]] | |||
[[Category:Orson]] | |||
Latest revision as of 17:01, 18 February 2025
| ← 136edo | 137edo | 138edo → |
137 equal divisions of the octave (abbreviated 137edo or 137ed2), also called 137-tone equal temperament (137tet) or 137 equal temperament (137et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 137 equal parts of about 8.76 ¢ each. Each step represents a frequency ratio of 21/137, or the 137th root of 2.
Theory
137edo is a fairly accurate 5-limit temperament and also a strong no-7 19-limit temperament. The equal temperament tempers out 2109375/2097152 (semicomma), [-13 17 -6⟩ (graviton), [8 14 -13⟩ (parakleisma), and [-29 -11 20⟩ (gammic comma) in the 5-limit. Using the patent val, it tempers out 225/224, 1728/1715, 2430/2401 in the 7-limit; 243/242 in the 11-limit; 351/350 in the 13-limit; 375/374 and 442/441 in the 17-limit; and 324/323 and 495/494 in the 19-limit. It provides the optimal patent val for 7-limit orwell temperament and for the planar temperament tempering out 2430/2401.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | -1.23 | -0.91 | +3.44 | +0.51 | +0.35 | +0.15 | +0.30 | +2.38 | +4.00 | +2.41 |
| Relative (%) | +0.0 | -14.0 | -10.4 | +39.2 | +5.8 | +4.0 | +1.8 | +3.4 | +27.2 | +45.7 | +27.5 | |
| Steps (reduced) |
137 (0) |
217 (80) |
318 (44) |
385 (111) |
474 (63) |
507 (96) |
560 (12) |
582 (34) |
620 (72) |
666 (118) |
679 (131) | |
Subsets and supersets
137edo is the 33rd prime edo, following 131edo and before 139edo. 274edo, which doubles it, provides a correction for its approximation to harmonic 7.
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [-217 137⟩ | [⟨137 217]] | +0.3865 | 0.3866 | 4.41 |
| 2.3.5 | [-21 3 7⟩, [-13 17 -6⟩ | [⟨137 217 318]] | +0.3887 | 0.3157 | 3.60 |
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperaments |
|---|---|---|---|---|
| 1 | 3\137 | 26.28 | 1594323/1562500 | Sfourth (5-limit) |
| 1 | 4\137 | 35.04 | 1990656/1953125 | Gammic (137d) / gammy (137) |
| 1 | 31\137 | 271.53 | 75/64 | Orwell (137e) / sabric (137d) |
| 1 | 36\137 | 315.33 | 6/5 | Parakleismic |
| 1 | 53\137 | 464.23 | 72/55 | Borwell |
| 1 | 59\137 | 516.79 | 27/20 | Marvo (137) |
| 1 | 63\137 | 551.82 | 11/8 | Emka (137d) / emkay (137) |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
Diagrams
A diagram of 7-limit orwell based on the 31\137edo generator: