User:CompactStar/Overtone scale: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
CompactStar (talk | contribs)
5,020 edits
No edit summary
CompactStar (talk | contribs)
5,020 edits
No edit summary
 
(13 intermediate revisions by the same user not shown)
Line 1: Line 1:
An '''overtone scale''' is an octave-long subset of the [[harmonic series]] repeating at the octave. An overtone scale has also be referred to as '''ADO''' (arithmetic divisions of the octave) due to an overtone scale being an arithmetically equal division of the octave.  
An '''overtone scale''' is an octave-long subset of the [[harmonic series]] repeating at the octave. It is also known as an '''AFDO''' (arithmetic frequency divisions of the octave) due to an overtone scale being an arithmetically equal division of the octave, and '''ODO''' ([[otonal division]]s of the octave).


An overtone scale with n notes maybe referred to as mode n of the [[harmonic series]] or n-ADO. For example, [[Mode 5]] is a pentatonic scale with the intervals [[1/1]]-[[6/5]]-[[7/5]]-[[8/5]]-[[9/5]]-[[2/1]]:
An overtone scale with n notes maybe referred to as mode n of the [[harmonic series]] or n-AFDO. For example, [[Mode 5]] is a pentatonic scale with the intervals [[1/1]]-[[6/5]]-[[7/5]]-[[8/5]]-[[9/5]]-[[2/1]] or the 5th to 10th harmonics:


{| class="wikitable"
{| class="wikitable"
Line 35: Line 35:
R_n = R_1 + (n-1)d
R_n = R_1 + (n-1)d
</math>
</math>
== Over-n scales ==
Another way to describe Mode 5 is that it is an example of an "Over-5 Scale." As 5 is octave-redundant with 10, 20, 40, 80 etc, any scale with one of those (the form is technically 2<sup>n</sup>*5, where n is any integer greater than or equal to zero) in the denominator of every tone could be called an Over-5 Scale.
== Lengths ==
If the first division has ratio of R1 and length of L1 and the last, Rn and Ln , we have: Ln = 1/Rn and if Rn &gt;........&gt; R3 &gt; R2 &gt; R1 so :
L1 &gt; L2 &gt; L3 &gt; …… &gt; Ln
[[File:ADO-4.jpg|350px|center]]
This lengths are related to reverse of ratios in system.The above picture shows the differences between divisions of length in Mode 12 system . On the contrary , we have equal divisions of length in **[https://sites.google.com/site/240edo/equaldivisionsoflength(edl) EDL system]**:
[[File:ADO-5.jpg|346px|center]]
== Relation to superparticular ratios ==
An overtone scale has step sizes of [[superparticular ratio]]s with increasing numerators. For example, [[Mode 5]] has step sizes of [[6/5]], [[7/6]], [[8/7]], and [[9/8]].
== Relation to otonality ==
We can consider an overtone scale system as otonal system. Otonality is a term introduced by Harry Partch to describe chords whose notes are the overtones (multiples) of a given fixed tone.Considering ADO , an Otonality is a collection of pitches which can be expressed in ratios that have equal denominators. For example, 1/1, 5/4, and 3/2 form an otonality because they can be written as 4/4, 5/4, 6/4. Every Otonality is therefore part of the harmonic series. An otonality corresponds to an arithmetic series of frequencies or a harmonic series of wavelengths or distances on a string instrument.
== Primodality ==
[[Primodality]] involves the use of large prime modes of the harmonic series.
== A solfege system ==
[[Andrew Heathwaite]] proposes a solfege system for harmonics 16-32 (Mode 16):
{| class="wikitable"
|-
| harmonic
| 16
| 17
| 18
| 19
| 20
| 21
| 22
| 23
| 24
| 25
| 26
| 27
| 28
| 29
| 30
| 31
| 32
|-
| JI ratio
| 1/1
| 17/16
| 9/8
| 19/16
| 5/4
| 21/16
| 11/8
| 23/16
| 3/2
| 25/16
| 13/8
| 27/16
| 7/4
| 29/16
| 15/8
| 31/16
| 2/1
|-
| solfege
| '''do'''
| '''ra'''
| '''re'''
| '''me'''
| '''mi'''
| '''fe'''
| '''fu'''
| '''su'''
| '''sol'''
| '''le'''
| '''lu'''
| '''la'''
| '''ta'''
| '''tu'''
| '''ti'''
| '''da'''
| '''do'''
|}
Thus, the pentatonic scale in the example at the top (Mode 5) could be sung: '''mi sol ta do re mi'''
== Twelve scales ==
For those interested in learning to sing and hear just intervals, here are twelve of the simplest otonal scales to try. I leave it up to the curious learner to decide the value, beauty, or usefulness of these particular scales for their compositional purposes.
{| class="wikitable"
|-
|
|
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
| 16
| 17
| 18
| 19
| 20
| 21
| 22
| 23
| 24
|-
| Mode 1
| 1-note
| '''do'''
| '''do'''
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|-
| Mode 2
| 2-note
|
| '''do'''
| '''sol'''
| '''do'''
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|-
| Mode 3
| 3-note
|
|
| '''sol'''
| '''do'''
| '''mi'''
| '''sol'''
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|-
| Mode 4
| 4-note
|
|
|
| '''do'''
| '''mi'''
| '''sol'''
| '''ta'''
| '''do'''
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|-
| Mode 5
| 5-note
|
|
|
|
| '''mi'''
| '''sol'''
| '''ta'''
| '''do'''
| '''re'''
| '''mi'''
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|-
| Mode 6
| 6-note
|
|
|
|
|
| '''sol'''
| '''ta'''
| '''do'''
| '''re'''
| '''mi'''
| '''fu'''
| '''sol'''
|
|
|
|
|
|
|
|
|
|
|
|
|-
| Mode 7
| 7-note
|
|
|
|
|
|
| '''ta'''
| '''do'''
| '''re'''
| '''mi'''
| '''fu'''
| '''sol'''
| '''lu'''
| '''ta'''
|
|
|
|
|
|
|
|
|
|
|-
| Mode 8
| 8-note
|
|
|
|
|
|
|
| '''do'''
| '''re'''
| '''mi'''
| '''fu'''
| '''sol'''
| '''lu'''
| '''ta'''
| '''ti'''
| '''do'''
|
|
|
|
|
|
|
|
|-
| Mode 9
| 9-note
|
|
|
|
|
|
|
|
| '''re'''
| '''mi'''
| '''fu'''
| '''sol'''
| '''lu'''
| '''ta'''
| '''ti'''
| '''do'''
| '''ra'''
| '''re'''
|
|
|
|
|
|
|-
| Mode 10
| 10-note
|
|
|
|
|
|
|
|
|
| '''mi'''
| '''fu'''
| '''sol'''
| '''lu'''
| '''ta'''
| '''ti'''
| '''do'''
| '''ra'''
| '''re'''
| '''me'''
| '''mi'''
|
|
|
|
|-
| Mode 11
| 11-note
|
|
|
|
|
|
|
|
|
|
| '''fu'''
| '''sol'''
| '''lu'''
| '''ta'''
| '''ti'''
| '''do'''
| '''ra'''
| '''re'''
| '''me'''
| '''mi'''
| '''fe'''
| '''fu'''
|
|
|-
| Mode 12
| 12-note
|
|
|
|
|
|
|
|
|
|
|
| '''sol'''
| '''lu'''
| '''ta'''
| '''ti'''
| '''do'''
| '''ra'''
| '''re'''
| '''me'''
| '''mi'''
| '''fe'''
| '''fu'''
| '''su'''
| '''sol'''
|}
== Individual pages for overtone scales ==
* [[Mode 2]]
* [[Mode 3]]
* [[Mode 4]]
* [[Mode 5]]
* [[Mode 6]]
* [[Mode 7]]
* [[Mode 8]]
* [[Mode 9]]
* [[Mode 10]]
* [[Mode 11]]
* [[Mode 12]]
* [[Mode 13]]
* [[Mode 14]]
* [[Mode 15]]
* [[Mode 16]]
* [[Mode 17]]
* [[Mode 18]]
* [[Mode 19]]
* [[Mode 20]]
* [[Mode 21]]
* [[Mode 22]]
* [[Mode 23]]
* [[Mode 24]]
* [[Mode 25]]
* [[Mode 26]]
* [[Mode 27]]
* [[Mode 28]]
* [[Mode 29]]
* [[Mode 30]]
* [[Mode 31]]
* [[Mode 32]]
* [[Mode 60]]
* [[Mode 120]]
== See also ==
* [[Arithmetic temperament]]
* [[Arithmetic MOS scale]]
* [http://240edo.googlepages.com/ADO-EDL.XLS Fret position calculator] (excel sheet) based on EDL system and string length
* How to approximate EDO and ADO systems with each other? [https://sites.google.com/site/240edo/ADOandEDO.xls Download this file]
* [http://www.soundtransformations.btinternet.co.uk/Danerhudyarthemarmonicseries.htm Magic of Tone and the Art of Music by the late Dane Rhudyar]
* [[Primodality]]
* [[8th Octave Overtone Tuning]]

Latest revision as of 02:40, 3 June 2024

An overtone scale is an octave-long subset of the harmonic series repeating at the octave. It is also known as an AFDO (arithmetic frequency divisions of the octave) due to an overtone scale being an arithmetically equal division of the octave, and ODO (otonal divisions of the octave).

An overtone scale with n notes maybe referred to as mode n of the harmonic series or n-AFDO. For example, Mode 5 is a pentatonic scale with the intervals 1/1-6/5-7/5-8/5-9/5-2/1 or the 5th to 10th harmonics:

harmonic 5 6 7 8 9 10
JI ratio 1/1 6/5 7/5 8/5 9/5 2/1

A "mode" in other musical contexts is usually a different rotation of the same intervals. In the case of different harmonic modes, that's not exactly the case. However, in some sense it's a reasonable comparison, because as you slide the subset of harmonics around, you're essentially sampling different segments of integers whose prime factorizations follow simple, constant patterns (every 2nd number has a 2, every 3rd number has a 3, every 5th number has a 5) and therefore the full internal interval set (all dyads, triads, tetrads, etc.) from one mode to the next is more alike than it is different.

For a Mode C system, the m-th degree is equal to the ratio (C+m)/C. If the first division is [math]\displaystyle{ R_1 }[/math] (which is ratio of C/C) and the last , [math]\displaystyle{ R_n }[/math] (which is ratio of 2C/C), with common difference of d

(which is 1/C), we have :

[math]\displaystyle{ R_2 = R_1 + d \\ R_3= R_1 + 2d \\ R_4 = R_1 + 3d \\ \vdots \\ R_n = R_1 + (n-1)d }[/math]


Over-n scales

Another way to describe Mode 5 is that it is an example of an "Over-5 Scale." As 5 is octave-redundant with 10, 20, 40, 80 etc, any scale with one of those (the form is technically 2n*5, where n is any integer greater than or equal to zero) in the denominator of every tone could be called an Over-5 Scale.

Lengths

If the first division has ratio of R1 and length of L1 and the last, Rn and Ln , we have: Ln = 1/Rn and if Rn >........> R3 > R2 > R1 so :

L1 > L2 > L3 > …… > Ln

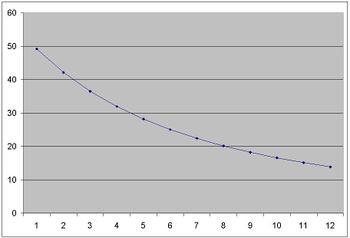
This lengths are related to reverse of ratios in system.The above picture shows the differences between divisions of length in Mode 12 system . On the contrary , we have equal divisions of length in **EDL system**:

Relation to superparticular ratios

An overtone scale has step sizes of superparticular ratios with increasing numerators. For example, Mode 5 has step sizes of 6/5, 7/6, 8/7, and 9/8.

Relation to otonality

We can consider an overtone scale system as otonal system. Otonality is a term introduced by Harry Partch to describe chords whose notes are the overtones (multiples) of a given fixed tone.Considering ADO , an Otonality is a collection of pitches which can be expressed in ratios that have equal denominators. For example, 1/1, 5/4, and 3/2 form an otonality because they can be written as 4/4, 5/4, 6/4. Every Otonality is therefore part of the harmonic series. An otonality corresponds to an arithmetic series of frequencies or a harmonic series of wavelengths or distances on a string instrument.

Primodality

Primodality involves the use of large prime modes of the harmonic series.

A solfege system

Andrew Heathwaite proposes a solfege system for harmonics 16-32 (Mode 16):

harmonic 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
JI ratio 1/1 17/16 9/8 19/16 5/4 21/16 11/8 23/16 3/2 25/16 13/8 27/16 7/4 29/16 15/8 31/16 2/1
solfege do ra re me mi fe fu su sol le lu la ta tu ti da do

Thus, the pentatonic scale in the example at the top (Mode 5) could be sung: mi sol ta do re mi

Twelve scales

For those interested in learning to sing and hear just intervals, here are twelve of the simplest otonal scales to try. I leave it up to the curious learner to decide the value, beauty, or usefulness of these particular scales for their compositional purposes.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Mode 1 1-note do do
Mode 2 2-note do sol do
Mode 3 3-note sol do mi sol
Mode 4 4-note do mi sol ta do
Mode 5 5-note mi sol ta do re mi
Mode 6 6-note sol ta do re mi fu sol
Mode 7 7-note ta do re mi fu sol lu ta
Mode 8 8-note do re mi fu sol lu ta ti do
Mode 9 9-note re mi fu sol lu ta ti do ra re
Mode 10 10-note mi fu sol lu ta ti do ra re me mi
Mode 11 11-note fu sol lu ta ti do ra re me mi fe fu
Mode 12 12-note sol lu ta ti do ra re me mi fe fu su sol

Individual pages for overtone scales

See also

Retrieved from "https://en.xen.wiki/index.php?title=User:CompactStar/Overtone_scale&oldid=145590"