User:VectorGraphics/Neutral Just System
The Neutral Just System is a system derived by Vector Graphics to notate just intonation and equal temperaments.
The Pythagorean chain of fifths is taken as the base, with alterations stemming from there, much like in most other systems. However, the Pythagorean base is also extended with neutral (that is, irrational) intervals, to better capture the characteristics of intervals in the 11- and 13-limit. In other words, the formal commas for 11 and 13 define their respective harmonics by altering a Pythagorean neutral interval, and for consistency, there will be ways to notate arbitrary divisions of any accidental.
3-limit: The chromatic semitone and Pythagorean comma

Usually, only one pair of accidentals is necessary for the 3-limit, but for completeness, I have provided a second accidental for the Pythagorean comma, to account for the 2-dimensional nature of 3-limit radical intonation. The accidental's design is inspired by a letter "C", for "Compton" (basing it off of a "P" for "Pythagorean" might lead to ambiguity with (semi)flats). This technically means that many intervals have multiple spellings
How to divide an accidental

The NJS is unique for supporting equal divisions of any accidental in the system. To transform any accidental into its "semi-" version, place an underline below the augmenting accidental or an overline above the diminishing accidental. These lines can stack. There is an exception for standard semisharps and semiflats. Similarly, to divide an accidental into three, a dot is placed below the augmenting form or above the diminishing form, below any underlines or above any overlines. Any remaining factor one wishes to divide by, with factors of 2 and 3 removed, is placed as an Arabic numeral in the space unoccupied by dots or lines (above an augmenting form or below a diminishing form). (So, for example, to divide a sharp into fifteen, one would write a dot below the sharp and a "5" above it). Finally, any accidental other than the normal sharp or flat contains an arrow or wedge shape which can be copied horizontally to the accidental's left to multiply its value (though often it is more convenient to use multiple accidentals). An example is provided on the right.
Formal commas
With this said, let us proceed to define the formal accidentals for each prime. As a principle, despite the capacity for splitting that this system presents, these will allow each harmonic to be found only as an alteration of intervals generated by the neutral chain of fifths (the system generated by a hemipythagorean neutral fifth and an octave).
This means that, for example, the 3edf-step (the 1/3-sharp 1/3-pythflat major second) is unrelated to the septimal major second.
Each accidental has an ASCII prefix form made of an initial and then the direction of the accidental. Initials are always written in lowercase to avoid confusion with note names (i.e. "C^" could be confused for a sharpened C note in another system, but "c^" is unambiguous).
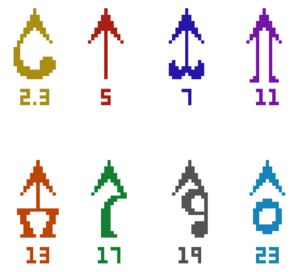
| Subgroup | Comma | Prefix | ASCII | Etymology |
|---|---|---|---|---|
| 2.3 | 2187/2048 | (none) | #, b | Inherited from standard notation |
| 2.3 | 531441/524288 | pyth- | c^, cv | Pythagorean comma, compton comma (initial chosen to match notation) |
| 2.3.5 | 81/80 | syn- | i^, iv | Syntonic comma, "i" chosen for visual similarity to the vertical bar of the arrow. |
| 2.3.7 | 64/63 | arch- | a^, av | Archytas' comma |
| 2.3.11 | 243/242 | rast- | r^, rv | Rastma |
| 2.3.13 | 512/507 | trid- | t^, tv | "Tridecimal", "harm-" would have had conflicting initial h- |
| 2.3.17 | 4131/4096 | hunt- | h^, hv | Comma is labelled as the "Hunt flat 2" comma |
| 2.3.19 | 513/512 | sev- | s^, sv | "Severinus", name of Boethius; "boeth-" would have had confusing initial <b> |
| 2.3.23 | 736/729 | jame- | j^, jv | "James Tenney", "Tenney" would have had conflicting initial t- |