Kite Guitar
Overview
The main website at KiteGuitar.com has audio, video, photos and scores
This is a brief explanation, see also the longer one at Kite Guitar explanation for non-microtonalists.
The Kite guitar (or bass, mandolin, banjo, etc.) combines the beauty of just intonation with the freedom of an equal temperament. Kite guitar is short for Kite-fretted guitar. It has 41 notes per the octave instead of 12. 41-tET aka 41-equal aka 41edo approximates 7-limit just intonation to within 3-6 cents, and chords sound gorgeous! But a guitar with 41 frets per octave is physically challenging to play. Kite-fretting cleverly omits every other fret. Thus while the frets are closer together than a standard guitar, the Kite guitar is still quite playable. There are 20½ frets per octave, thus it's about as playable as 19-equal or 22-equal. The interval between open strings is usually 13 steps of 41. Because 13 is an odd number, all 41 pitches are present on the guitar. Each string has only half of the pitches, but any adjacent pair of strings has all 41.
Omitting half the frets (known as skip-fretting) in effect moves certain pitches to remote areas of the fretboard, and makes certain intervals difficult to play. Magically, it works out that the remote intervals are the ones that don't work well in chords, and the ones that aren't remote are the ones that do work well. For example, the sweet 5-limit major 3rd, a 5/4 ratio, is easily accessible, but the dissonant 3-limit major 3rd 81/64 isn't. (3-limit & 5-limit refer to the largest prime number in the frequency ratio.)
In addition, important 7-limit intervals like 7/6, 7/5 and 7/4 are easy to play. This means the Kite guitar can do much more than just play sweet Renaissance music. It can put a whole new spin on jazz, blues and experimental music. The dom7 and dom9 chords are especially calm and relaxed, revealing just how poorly 12-equal tunes these chords. But dissonance is still possible, in fact 41-equal can be far more dissonant than 12-equal. And 41 notes means that the melodic and harmonic vocabulary is greatly expanded, allowing truly unique music that simply isn't possible with 12 notes.
The interval between open strings is usually a major 3rd, not a 4th. Thus new chord shapes must be learned. However, the Kite guitar is isomorphic, meaning that chord shapes can be moved not only from fret to fret but also from string to string. Thus there are far fewer shapes to learn. (Open tunings, which are non-isomorphic, are also possible.) Tuning in 3rds not 4ths reduces the overall range of the guitar. Thus a 7-string or even an 8-string guitar is desirable.
See also this Now and Xen podcast: 29.268¢-kite-giedraitis-aaron-wolf-spencer-hargraves-jacob-collier. Kite Giedraitis and Aaron Wolf were hanging out one afternoon playing Kite guitar, when Spencer Hargraves (Terry Maple, Jock Tears, Redrick Sultan) texted that he had a gig that night in Portland. They invited him over, and excitedly filled him in on the Kite guitar. Later Spencer told them he had secretly recorded the conversation.
About 41-equal
41-equal (aka 41edo) has steps of 29.27¢. It approximates 7-limit just intonation very closely. Prime 3 is extremely accurate, and primes 5 and 7 are both tuned slightly flat, which means their errors partially cancel out in ratios such as 7/5. Prime 11 is also quite accurate. But unfortunately it's tuned sharp, so the errors can add up, and 11/10 is nearly 11¢ sharp. Primes 13 and 17 are further off, and accurate intonation requires microbending.
| prime | 2/1 | 3/2 | 5/4 | 7/4 | 11/8 | 13/8 | 17/16 | 19/16 |
|---|---|---|---|---|---|---|---|---|
| error | 0.0¢ | +0.48¢ | -5.8¢ | -3.0¢ | +4.8¢ | +8.3¢ | +12.1¢ | -4.8¢ |
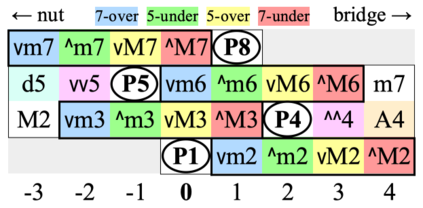
The 41 notes can be named with ups and downs. A sharp equals four arrows (two frets), and a minor 2nd equals three arrows.
| C | ^C | ^^C = vvC# | vC# | C# | ^C# | ^^C# | |
| vvDb | vDb | Db | ^Db | ^^Db = vvD | vD | D |
| P1 | ^1 | ^^1 = vvA1 | vA1 | A1 | ^A1 | ^^A1 | |
| vvm2 | vm2 | m2 | ^m2 | ~2 | vM2 | M2 |
All 41 intervals (P = perfect, ~ = mid):
- P1 ^1
- vm2 m2 ^m2 ~2 vM2 M2 ^M2
- vm3 m3 ^m3 ~3 vM3 M3 ^M3
- v4 P4 ^4
- ~4/vd5 vA4/d5 A4/^d5 ^A4/~5
- v5 P5 ^5
- vm6 m6 ^m6 ~6 vM6 M6 ^M6
- vm7 m7 ^m7 ~7 vM7 M7 ^M7
- v8 P8
The most dissonant intervals are the off-perfect ones ^1, v4, ^4, v5, ^5 and v8.
| cents | degree | Ups and downs notation | in C | solfege | ||
|---|---|---|---|---|---|---|
| 0 | 0¢ | 1sns | perfect unison | P1 | C | Da |
| 1 | 29 | up-unison | ^1 | ^C | Du | |
| 2 | 59 | 2nds | downminor 2nd | vm2 | vDb | Fro |
| 3 | 88 | minor 2nd | m2 | Db | Fra | |
| 4 | 117 | upminor 2nd | ^m2 | ^Db | Fru | |
| 5 | 146 | mid 2nd | ~2 | vvD | Ri | |
| 6 | 176 | downmajor 2nd | vM2 | vD | Ro | |
| 7 | 205 | major 2nd | M2 | D | Ra | |
| 8 | 234 | upmajor 2nd | ^M2 | ^D | Ru | |
| 9 | 263 | 3rds | downminor 3rd | vm3 | vEb | No |
| 10 | 293 | minor 3rd | m3 | Eb | Na | |
| 11 | 322 | upminor 3rd | ^m3 | ^Eb | Nu | |
| 12 | 351 | mid 3rd | ~3 | vvE | Mi | |
| 13 | 380 | downmajor 3rd | vM3 | vE | Mo | |
| 14 | 410 | major 3rd | M3 | E | Ma | |
| 15 | 439 | upmajor 3rd | ^M3 | ^E | Mu | |
| 16 | 468 | 4ths | down-4th | v4 | vF | Fo |
| 17 | 498 | perfect 4th | P4 | F | Fa | |
| 18 | 527 | up-4th | ^4 | ^F | Fu | |
| 19 | 556 | tritones | mid-4th / downdim 5th | ~4 / vd5 | ^^F / vGb | Fi / Sho |
| 20 | 585 | downaug 4th / dim 5th | vA4 / d5 | vF# / Gb | Po / Sha | |
| 21 | 615 | aug 4th / updim 5th | A4 / ^d5 | F# / ^Gb | Pa / Shu | |
| 22 | 644 | upaug 4th / mid-5th | ^A4 / ~5 | ^F# / vvG | Pu / Si | |
| 23 | 673 | 5ths | down-5th | v5 | vG | So |
| 24 | 702 | perfect 5th | P5 | G | Sa | |
| 25 | 732 | up-5th | ^5 | ^G | Su | |
| 26 | 761 | 6ths | downminor 6th | vm6 | vAb | Flo |
| 27 | 790 | minor 6th | m6 | Ab | Fla | |
| 28 | 820 | upminor 6th | ^m6 | ^Ab | Flu | |
| 29 | 849 | mid 6th | ~6 | vvA | Li | |
| 30 | 878 | downmajor 6th | vM6 | vA | Lo | |
| 31 | 907 | major 6th | M6 | A | La | |
| 32 | 937 | upmajor 6th | ^M6 | ^A | Lu | |
| 33 | 966 | 7ths | downminor 7th | vm7 | vBb | Tho |
| 34 | 995 | minor 7th | m7 | Bb | Tha | |
| 35 | 1024 | upminor 7th | ^m7 | ^Bb | Thu | |
| 36 | 1054 | mid 7th | ~7 | vvB | Ti | |
| 37 | 1083 | downmajor 7th | vM7 | vB | To | |
| 38 | 1112 | major 7th | M7 | B | Ta | |
| 39 | 1141 | upmajor 7th | ^M7 | ^B | Tu | |
| 40 | 1171 | 8ves | down 8ve | v8 | vC | Do |
| 41 | 1200 | perfect 8ve | P8 | C | Da | |
These charts show the intervals and the notes of the conventional 12-equal (aka 12-edo) tuning as circles of 5ths.
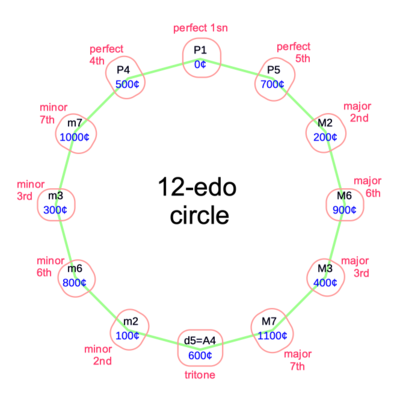
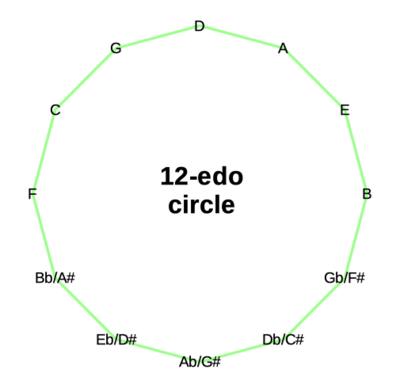
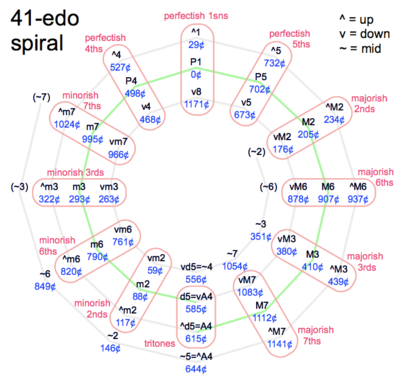
These charts show 41-equal in terms of 12-equal. The circle of fifths becomes a spiral. Because this spiral is really a circle of 41 fifths, the two innermost and two outermost intervals are duplicates. In the first chart, "-ish" means ±1 edostep (one 41st of an octave).

Tunings
Unfortunately, tuning the Kite guitar to EADGBE causes the conventional chord shapes to have wolfy offperfect intervals that are only 1 edostep away from perfect. For example, the usual E major chord shape 0 2 2 1 0 0 would translate to either 0 3 3 2 0 0 = E vB vE G# B E, or else 0 4 4 2 0 0 = E ^B ^E G# B E. Either way, the chord contains three offperfect octaves and two offperfect fifths. (In addition, the major 3rd isn't 5/4 but 81/64.) The usual Em, A, Am, D, Dm, G and C chord shapes also have offperfect intervals. The tuning can be slightly adjusted so that one of these chord shapes is in tune. For example, E ^A ^D ^G B E puts E downmajor = 0 3 3 1 0 0 in tune, as well as E upminor = 0 3 3 0 0 0. While this is an improvement, the other chord shapes still have offperfect intervals. No adjustment to EADGBE will get more than a few of the conventional chord shapes in tune. Thus learning new chord shapes is inevitable.
There are two main types of tunings. Isomorphic tunings in 3rds facilitate playing 7-limit chords and chord progressions, and exploring the 7-limit lattice. Open tunings such as DADGAD facilitate exploring the 13-limit tonality diamond.
There are two types of Kite guitar fretboards, even-frets and odd-frets. In the former, all or almost all of the frets are an even number of edosteps from the nut. In the latter, it's an odd number. In general, the even-fret layout is for isomorphic (or dimorphic, see below) tunings and the odd-frets layout is for open tunings.
Isomorphic means "same shape", and there is only one shape to learn for any chord. The standard isomorphic tuning is the downmajor tuning, in which adjacent open strings are tuned a downmajor 3rd apart. Alternative isomorphic tunings use an upminor 3rd or an upmajor 3rd. Two possible dimorphic ("two shapes") tunings are the alternating thirds tuning (alternates downmajor 3rds with upminor 3rds), and the plain tuning (alternates plain perfect 4ths with plain major 2nds). The drawback to dimorphism is that every chord has two shapes. The advantage is that the open strings make a diatonic scale. The trimorphic ("three shapes") Russian tuning is based on the traditional Russian tuning DGBDGBD, but with vB not B.
- Fretboard chart for the downmajor tuning
- Fretboard chart for the upminor tuning
- Fretboard chart for the DADGAD tuning
DADGAD lacks both the 4th and the rainbow of four 6ths in the lower octave. A seven-string DGADGAD tuning remedies this.
Open tunings become more playable with the use of a "half-fret capo". From Deja Igliashon's liner notes (see the Recordings section):
"A couple of improvisations on a guitar loaned to me by Kite Giedratis. The guitar is fretted to 41 notes per double-octave, i.e. every other note of 41 notes per octave, using movable cable ties. On these tracks I modified the fretting slightly by moving the 2nd fret down one step of 41edo and then put a capo behind it, effectively moving all the frets above it UP by one step of 41edo, so that the frets all give odd-numbered pitches from 41edo instead of even-numbered ones. This gives frets for approximations to the ratios 21/20, 12/11, 9/8, 7/6, 6/5, 5/4, 9/7, 4/3, 11/8, and 10/7 relative to the open strings, which makes it possible to let the open strings ring out against pitches fretted low on the neck when the open strings are tuned to DADGAD or DGDGAD, my two favorite open tunings.
Without the offset I introduced, the normal fretting on Kite's guitar would have the lowest frets approximating 28/27, 16/15, 10/9, 8/7, 32/27, 11/9, 81/64, 15/11, 7/5, and 16/11, which doesn't work well for the open tunings I like but is rather designed to have the open strings tuned in parallel 3rds (5/4 or 6/5), for an isomorphic layout that facilitates chords built by stacking 3rds. I found that tuning somewhat challenging, being so unlike any open string tunings I've ever used before, and most of the intervals between non-adjacent open strings are rather discordant. Other players, whose styles don't lean as heavily on open strings and drones the way I do, may find Kite's original design preferable to my modification.
But anyway, the two designs can coexist on the same fretboard by simply inserting an extra fret between the 1st and 2nd instead of moving the 2nd fret lower as I have done, and by varying the tuning of the open strings as you please. It's a fantastic way to access the resources of 41edo on a guitar, without having an absurd number of very closely-spaced frets!"
Deja has since explored other open tunings besides DADGAD and DGDGAD, such as E A vC# vG B ^^D (a 3:4:5:7:9:11 chord) and D A D vF# vC E (a 2:3:4:5:7:9 chord). They prefer placing the first fret 3 edosteps above the nut. This creates a half-fret offset without a capo. A capo on the 1st fret could remove the half-fret offset, if desired.
How to implement the half-fret capo trick: An extra fret slot is cut to allow insertion of a temporary fret in between the nut and the 1st (permanent) fret, or if the action is too high to capo there, then between the 1st and 2nd (permanent) frets. The slot stops short of the treble side of the fretboard. So gravity holds it in place, plus of course the capo. The temporary fret has the barbs on the side of the tang filed off. The extra slot is a bit wider, so the fret can be pulled out easily. It goes in from the side, under the strings, so the strings don't need to be loosened. It can be inserted and removed on stage between songs. The fret is a bit longer, sticks out about 1 inch, so that you can pull it out easily. Putting a large piece of wide tape on the part that sticks out helps prevent it from being lost.
Alternatively, the extra fret can be a permanent one. The extra fret is indicated in tablature by a letter: "a" if it's between the nut and the 1st fret, "b" if it's between the 1st and 2nd frets, etc.
A d-fret makes a 9/8 interval with the nut. Combined with the alternating 3rds tuning, it makes playing 5-limit music in first position possible. A b-fret and/or an e-fret can also be useful.
Fretboard charts (downmajor tuning)
Relative charts (Intervals)
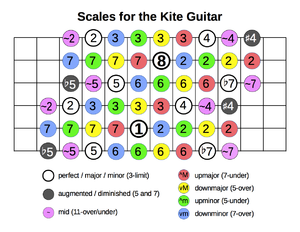
This chart is in relative not absolute notation, meaning it shows intervals not notes. At the bottom is P1, a perfect unison. This is the tonic of the scale, or the root of the chord. This chart shows all the intervals within easy reach of this note, up to an octave. There are four "rainbows": one of 2nds, one of 3rds, one of 6ths, and one of 7ths. These plus the 4th, 5th, various tritones and 2 other notes add up to 25 of the 41 notes. Every single ratio of odd-limit 9 or less appears here.
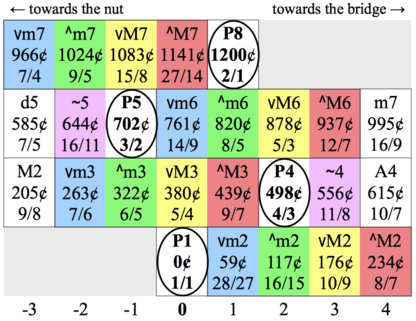
This chart boils the information down to the essentials: interval name and (via color) general type of ratio.
This chart is the same, but extends much further. Some ratios change in the higher octaves, e.g. 16/15 becomes not 32/15 but 15/7.
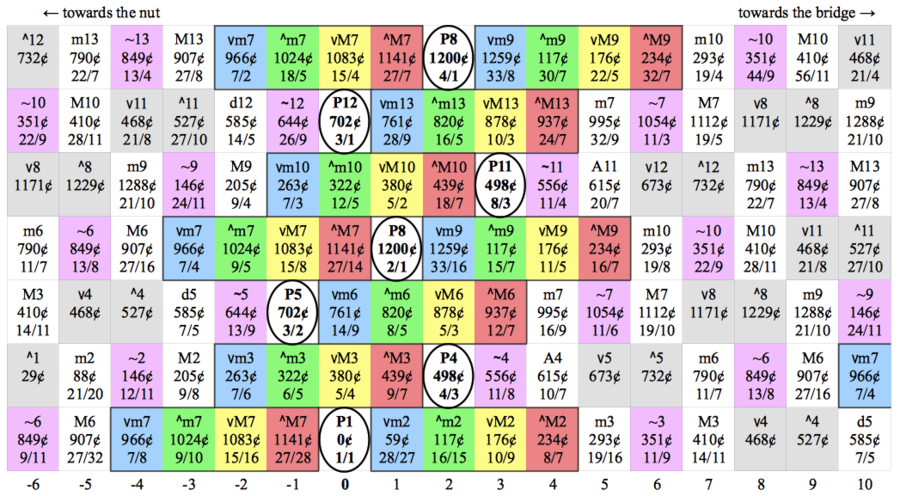
This chart extends even further, showing the "rainbow zones" and the "complex zones". When two guitarists play together, it's very natural for one to play chords in the lower rainbow zone, and another to solo in the higher rainbow zone. The open strings tend to be in a complex zone, unless the tonic is fairly close to the nut, or else up around the 3rd or 4th dot.
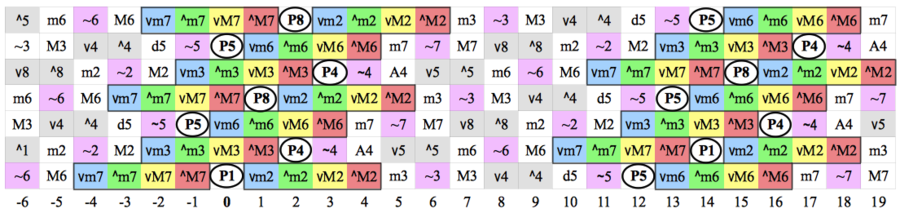
Absolute charts (notes)
The Kite Fretboard Visualizer Tool is a google spreadsheet that generates a fretboard showing all the notes of a chord or scale. Unhiding columns will reveal several extra frets. Here's the F downmajor scale:
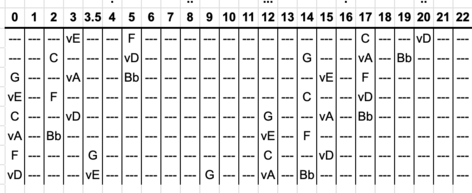
This chart shows the actual notes of an 8-string Kite guitar. The notes circled in red are the open strings of a 12-equal guitar. The ideal string gauges for this tuning are discussed in the How to make a Kite Guitar page. Every 4th fret has a set of one, two or three dots. Three dot sets equals a 5th. The dots run single-double-triple-single-double-triple etc. One set of single-double-triple is called a "kite" (due to its shape). There is a low kite, a mid kite and sometimes a high kite. Each dot set can be named low single, mid double, etc. See KDF Fret Numbering.
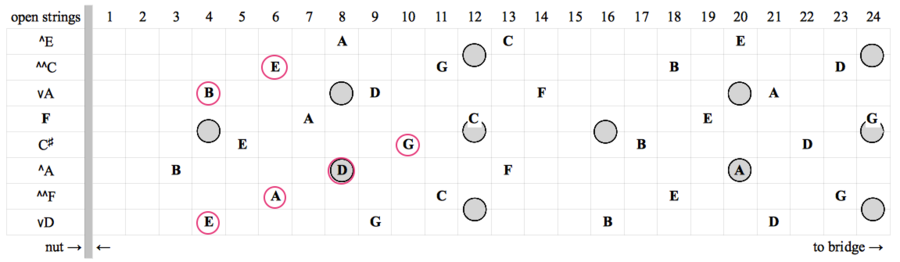
A 6-string guitar is usually tuned to the middle 6 strings of the full 8 strings:
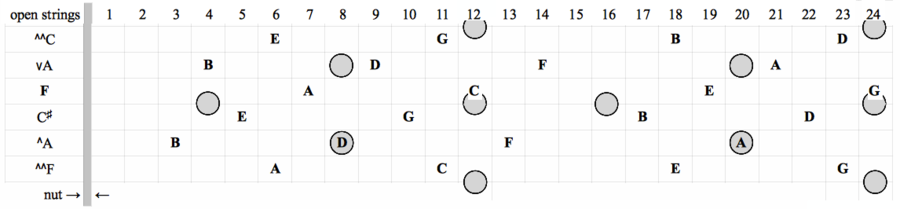
This is called the mid-6 tuning, as opposed to a low-6 tuning (vD to vA), or high-6 tuning (^A to ^E). Not to be confused with a lo-6 or hi-6 voicing, see Hi-lo notation and the chords page. In the table below, the less likely ranges are in parentheses.
| range | notes | |||||||
|---|---|---|---|---|---|---|---|---|
| full-8 | vD | ^^F | ^A | C# | F | vA | ^^C | ^E |
| high-7 | ^^F | ^A | C# | F | vA | ^^C | ^E | |
| low-7 | vD | ^^F | ^A | C# | F | vA | ^^C | |
| (high-6) | ^A | C# | F | vA | ^^C | ^E | ||
| mid-6 | ^^F | ^A | C# | F | vA | ^^C | ||
| (low-6) | vD | ^^F | ^A | C# | F | vA | ||
A 7-string guitar could possibly be a mid-7 (either high-7 down a dot, D# to D, or else low-7 up a dot, E to Eb). Another option is a baritone guitar tuned to the top 5 or 6 strings of the full-8, but lowered by an octave.
A bass guitar can of course be fretless and tuned EADG as usual. This avoids the need for extra strings and custom microtonal frets. If fretted, a bass would be tuned in major 3rds, similar to the lower strings of a Kite guitar but an octave lower. It would ideally have 6 strings. A conventional 5-string bass often has the 5th string tuned to B below low E. The analogous Kite bass has a Bb below the low vD. Tuning this way makes a deep-6 or deep-7 tuning.
| range | notes (bass) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| full-6 | vD | ^^F | ^A | C# | F | vA | |||
| (high-5) | ^^F | ^A | C# | F | vA | ||||
| low-5 | vD | ^^F | ^A | C# | F | ||||
| (high-4) | ^A | C# | F | vA | |||||
| mid-4 | ^^F | ^A | C# | F | |||||
| low-4 | vD | ^^F | ^A | C# | |||||
| deep-7 | Bb | vD | ^^F | ^A | C# | F | vA | ||
| deep-6 | Bb | vD | ^^F | ^A | C# | F | |||
| (deep-5) | Bb | vD | ^^F | ^A | C# | ||||
This chart shows all the notes for the full-8 tuning, not just the natural ones. But it's too much work to memorize all this. Just learn where the 7 natural notes are, and learn your intervals. Since the open strings don’t work as well, one tends to think more in terms of intervals than notes anyway.
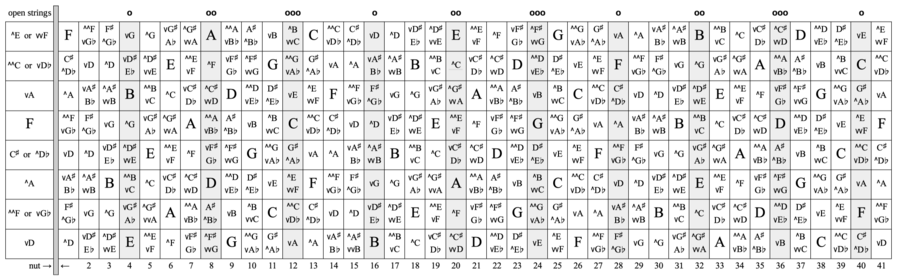
Some keys are somewhat awkward to play in. For example, a vG scale is either too close to the nut to have a plain major 2nd, or else way up at the 16th fret where the fret spacing is a little too cramped to play chords comfortably. There's a "sweet spot" for the tonic on the lowest 3 strings, from about the 4th fret to about the 11th fret. This defines a 3x8 rectangle containing 24 keys, roughly every other one of the 41 possible keys. The lowest string of an 8-string is tuned to vD not D so that the common keys of C, G, D, A and E fall in this sweet spot. D is tuned to A-440 standard pitch, to bring these 5 keys as close to 12-equal as possible. The D note agrees exactly, the A note is 2.5¢ sharp of 12-equal, E is 5¢ sharp, and so forth along the spiral of 5ths.
In 12-equal, all 12 keys are needed so that a vocalist can get within 50¢ of their optimal range. In 41-equal, using only these 24 keys, one can get within 30¢ of the optimal range. 30¢ from optimal is sufficient, 15¢ from optimal is overkill, so the other 17 keys aren't really needed. Unless a song modulates by a single edostep, then one might be forced to play up the neck in an awkward key. Here's all the notes of the mid-6 tuning:
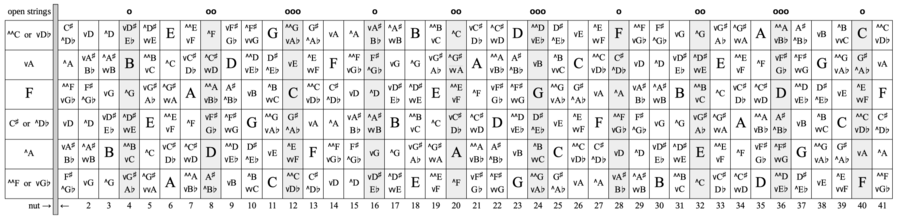
Kite guitars often have an extra fret between the nut and the first fret, called the a-fret, or between the first and second frets, called the b-fret. Capoing at this fret raises the open strings by one edostep, as these charts show. This moves the first rainbow zone closer to the nut, which can solve many arranging problems. Capoing also enables various open tunings such as DADGAD.
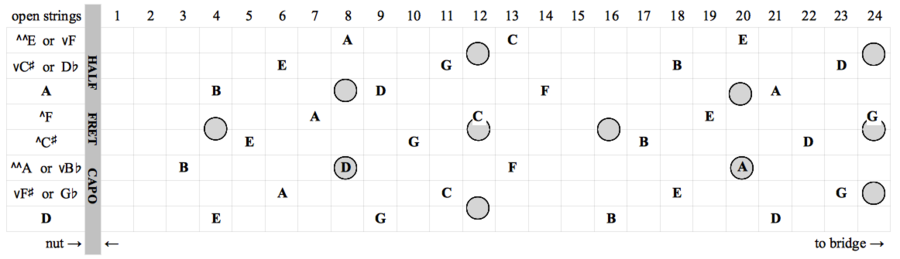

Chord shapes (downmajor tuning)
Main article: Kite Guitar Chord Shapes (downmajor tuning).
Chords are named using ups and down notation, see also the notation guide for edos 5-72. Briefly, an up or down in the chord name immediately after the root affects the 3rd, 6th and/or the 7th, but not the 5th or 9th. Chord progressions are written as Cv7 - vEb^m6 - Fv7 or Iv7 - vbIII^m6 - IVv7.
Here's a printer-friendly chart to get you started, with and without fingerings:
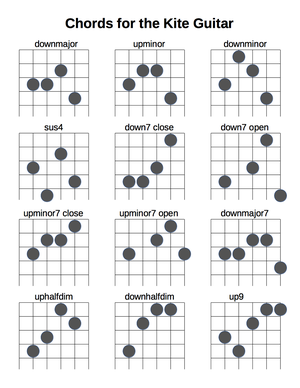

Scale shapes (downmajor tuning)
Main article: Kite Guitar Scales (practical guide)
See also: Categorizations of 41-equal Scales (theoretical background, the 5 categories of scales)
Printable charts, one of scale degrees, the other of the three main heptatonic scales. In the latter, some scale degrees appear more than once. In general, use the one that agrees with the current chord.

Relative and absolute tab
Since the fretboard is isomorphic, any interval can be expressed in relative tab as a vector. This is particularly useful for in-person oral instruction of chord shapes. For example, in the downmajor tuning, going up 2 strings and down 1 fret always takes you up a perfect 5th. In relative tab, that move is spoken as "plus-two, minus-one", and written as (+2,-1). The downmajor 2nd is at "oh, plus-three", (0,+3). The downmajor 3rd is at "plus-one, oh", (+1,0).
Every interval appears in several places on the fretboard. Typically one is within a few frets and another one is many frets away. Mentally grouping four frets together into one dot facilitates large jumps up and down the fretboard. For example, the octave is (+3,+1) and also (+1,+14). A jump of 14 frets is a "3 and 2" jump, meaning 3 dots plus 2 frets. Thus the octave is at "plus-one, plus-three-and-two", or (+1,+3+2). The 5th at (0,+3+0) is spoken as "oh, plus-three-and-none", or alternatively "oh, plus-three-dots". The unison is plus-two minus-three-and-one, (+2,-3-1). An upward jump of 11 frets could be called either plus-two-and-three or plus-three-minus-one. Note that plus-three-oh means up three strings, but plus-three-and-none means up three dots.
Notes can be referred to similarly in absolute tab, which names each string/fret combination, i.e. each location on the fingerboard using KDF fret numbering. For example, a low E on an 8-string is at "eighth single", written (8 ,0), meaning 8th string, low single dot. This is particularly useful when one wants to tell another guitarist what key they are in, without having to use note names. For example, one might be in the key of "sixth double three", (6 ₒₒ3) meaning 6th string, 3 frets above the low double dot. "Sixth and two" (6 2) means 6th string, 2nd fret. "Sixth and oh" (6 0) means the open 6th string.
Unlike relative tab, absolute tab doesn't require isomorphism, and can be applied to any guitar, as long as the dot locations are agreed on. Instead of counting kites, one simply numbers the dots directly, so KDF becomes DF. For 12-equal, dots are at frets 3, 5, 7, 9, 12, etc., thus the 10th fret is fourth-and-one. DF numbering can be applied to a Kite guitar with an odd-frets layout that puts dots on the harmonic series.
Note that in absolute tab, strings are numbered in descending order, but in relative tab, a positive move is an ascending move. Thus moving from the 3rd string to the 1st string is plus-two, not minus-two.
Tuning instructions
The Kite guitar in downmajor tuning can be tuned by ear using the octaves at (+1,+3+2) (see the explanation of relative tab in the previous section). The open 6th string should be an octave bellow the 5th string's 14th fret. This can be written as (6th, 0) = (5th, 3rd & 2). We can double-check the tuning using the unisons at (+2,-3-1). Thus the 6th string at the 13th fret should match the open 4th string, and (6th, 3rd & 1) = (4th, 0). Finally, the 3rd harmonic of the 6th string should match the open 1st string (technically it should be half a cent sharp of it).
These intervals are easily derived from the fact that going up 3 dots on any string equals going up a 5th. Start with any open string except the bottom two, go up a 5th by moving up 3 dots, then go down a 5th the usual way by moving (-2, +1). This is obviously a unison. Start at any open string except the top one, go up 3 dots, then go up a 4th by moving (+1, +2). This is obviously an octave.
Here are the full tuning instructions for a 6-string guitar:
| octaves | unisons |
|---|---|
| (6th, 0) = (5th, 3rd & 2) | (6th, 3rd & 1) = (4th, 0) |
| (5th, 0) = (4th, 3rd & 2) | (5th, 3rd & 1) = (3rd, 0) |
| (4th, 0) = (3rd, 3rd & 2) | (4th, 3rd & 1) = (2nd, 0) |
| (3rd, 0) = (2nd, 3rd & 2) | (3rd, 3rd & 1) = (1st, 0) |
| (2nd, 0) = (1st, 3rd & 2) | (6th, 0) harmonic at 3rd dot = (1st, 0) |
In the upminor tuning, the octave is at (+1,+3+3), and (6th, 0) = (5th, 3rd & 3). The unison is at (+2,-2-3), and (6th, 2nd & 3) = (4th, 0).
In the upmajor tuning, the octave is at (+1,+3+1), and (6th, 0) = (5th, 3rd & 1). The unison is at (+2,-3-3), and (6th, 3rd & 3) = (4th, 0).
Tuning software options
With a traditional 12-equal tuner, one method to get quite close is to fret either A or D on each string and get that in tune. For more precise 41-equal tuning, use a tuner that directly supports 41-equal. The following options are all open source and free of charge:
Microtonal-Tuner by Wilckerson Ganda is a browser-based app that works on Windows, OS X, Linux, Android and iOS. Source code on github.
Tuner (Google Play or Fdroid) by Michael Moessner is for Android only (note that multiple android apps have that name). Source code on github.
EDO tuner by John Watson is for iOS only. Source code on github.
EDO-strobeTuner by Kite Giedraitis functions as a DAW plug-in, and requires Reaper (small-footprint DAW for Windows, OS X or Linux) or ReaJS (Windows-only VST wrapper). Source code is in the text file itself.
LINGOT is a GNU/Linux tuner which supports any tuning system and imports scala files. To set it to 41-equal, download and import this 41-edo.scl file. Then, set the frequency of pitch "1" to D by replacing the "mid-C" text with the frequency number "587.33". Source code at the main link.
Guitarix is a GNU/Linux guitar-effects software which has 41-equal as a built-in tuning option. Source code at the link.
How to read 41-equal scores
Main article: How to read 41-equal scores (a crash course for non-guitarists)
Translating songs to 41-equal
Main article: Kite Guitar translations
Obviously, the Kite Guitar can do much more than simply play conventional music. But a good starting place is to take what you know and find it on the Kite Guitar. Translating 12-equal music is sometimes problematic but never impossible. Generally the translated version is an improvement, because it's so well tuned. There follows some general advice on translating:
A translation can be either extremely faithful (note-for-note), somewhat faithful (chord voicings are changed), or not faithful (reharmonization occurs). In all but the last case, if someone who doesn't know the original were to translate the song back to 12-equal, they should arrive at the original. Back-translation means simply removing all ups and downs. Back-translation requires proper spelling: vDvm must be spelled vD vvF vA not vD ^E vA.
A somewhat faithful translation may have a slight reharmonization. Perhaps adding notes to a chord (e.g. adding 7ths to triads), or omitting notes (e.g. dropping the 3rd or 5th of a 6add9 chord to avoid a wolf interval).
One way to translate a conventional song is to first translate it to 7-limit JI, perhaps visualizing it on a lattice, keeping in mind that 41-equal tempers out the Layo, Ruyoyo, Latrizo and Saruyo minicommas. Then translate the JI to 41-equal. Another way is to use the spiral charts in the "About 41-equal" section.
Often there is only one obvious way to translate a song. I - V - VIm - IV becomes Iv - Vv - vVI^m - IVv. Sometimes there are multiple obvious translations. For example, the first 3 chords of "When I Was Your Man" are II7 - IIm7 - I. That could become vII^7 - vII^m7 - Iv, or it could become ^IIv7 - ^IIvm7 - Iv.
In general, chords shouldn't use offperfect intervals (^4, v4, ^5, v5, ^8, v8, ^12 or v12). However ^11 and v11 are acceptable. Downmajor is preferred over upmajor. Upminor is preferred for most folk, but downminor is preferred for most blues. In general, avoid using plain major and minor 3rds and 6ths in a chord.
12-equal's augmented triads and dim7 tetrads can be translated many ways. Ia can become I^a, Iva, Iv(vv#5) or even I^(^^5). Furthermore the root can be changed, so that Ca becomes ^E^(^^5)/C. Likewise Cd7 can become not only C^d7 or Cvd7, but also ^Avd7/C or vA^d7/C. The latter two are equivalent to C^d6 and Cvd6.
Comma pumps, other than the aforementioned minicommas, cause pitch shifts, or occasionally, a tonic drift. The shift/drift is generally by a half-fret (a single edostep). Shifts of a full fret don't feel like shifts but more like reharmonizing/remelodizing, and full-fret drifts feel more like modulating.
The two most common commas that cause issues are the Gu and Ru commas. The choice of which two chords in the pump contain the pitch shift can be tricky. Generally, root movement by an offperfect interval is avoided. This usually necessitates a root movement by a plain major or plain minor interval.
For example, I - VIm - IIm - V7 - I is a Gu pump. Without the pump, I - VIm would be translated as Iv - vVI^m, to avoid shifts. The roots would move by a vM6. With the pump, this might translate to Iv - VI^m - II^m - Vv7 - Iv. The first root movement is by a M6. The tonic and the major 3rd both shift between the I chord and the VI chord.
Likewise, I7 - IV7 - V7 - I7 is a Ru pump. The usual translation is Iv7 - IVv7 - Vv7 - Iv7, with the scale's 4th shifting between the IV and V chords. Another example is Im7 - bIIIm6 - bVII7 - IV7 - I7. The root movements are m3, P5, P5, P5. Without the pump, the m3 movement would be translated to vm3. With the pump, to avoid an ^5 movement, the translation is Iv7 - bIII^m6 - bVIIv7 - IVv7 - I.
For rapid comma pumps of only two measures, a shift halfway through the pump is often best. See Kite's translation of "I Will".
One way to hide pitch shifts is to voice the two occurrences of the pitch in different octaves. Failing that, at least put them in a middle voice, not the top or bottom voice, so as to be less prominent. Another way is to omit the 5th in one of the chords. Thus in the Gu example, the 2nd chord might be VI^mno5. Another trick is to delay the entrance of the 2nd note a beat or two, or end the 1st note a little early. In a polyphonic context, it helps if the shifting note is in two voices of different timbres. If you're recording, you can pan the 2 close notes to different sides. Remember, the ear wants to hear the two notes as the same, and only needs a little encouragement to do so.
In much music, especially pre-20th-century music, the dissonance of the dom7 chord is what drives the V7 - I cadence and gives the music momentum. But 41-equal's smooth v7 chord is like a guard dog that smiles and wags its tail at strangers instead of barking. It's too relaxed! And the 7-limit intervals can sound out of place in a pre-20th-century context. One might instead use Vv,7 (down add-7, with a plain minor 7th) or Vv^7 (down up-7, with an upminor 7th). For example, Am - G - F - E7 can be translated as A^m - ^Gv - ^Fv - Ev^7. (This also avoids a pitch shift.)
For 20th-century music, a Vv7 chord is often appropriate. But when a stronger cadence to the I chord is desired, a V^7 chord often works better. For example, IIm7 - V7 - IM7 could be translated as either II^m7 - Vv7 - IvM7 or IIvm7 - Vv7 - IvM7. But the v7 chord is actually smoother than the vM7 chord, so both progressions feel unfinished. Often II^m7 - V^7 - IvM7 is better. The II^m7 chord has two notes in common with V^7. It feels somewhat like a V11noRno3 chord. If a 9th is added to the V^7 chord, there are three common notes, and the progression feels even more connected.
In IIm - V7 - I, where the I chord has no 7th, Vv7 works well. The progression can be tuned either II^m7 - Vv7 - Iv or IIvm7 - Vv7 - Iv. The IIvm7 chord is more connected to the V chord than II^m7. The Vv7 chord also works if the I chord has a minor 7th, i.e. Iv7.
These are all just guidelines, not hard and fast rules! There is often more than one good way to translate a song.
Translating microtonal material
Obviously 7-limit JI material translates easily. Material in either 19-equal or 22-equal usually translates fairy easily. 19-equal tempers out 81/80 but inflates 64/63 to a full edostep. Vice versa for 22-equal. (In fact, 41-equal is somewhat like a cross between the two edos. 41-equal's edomapping is the sum of those of 19 and 22 for most primes except 13 and 23.) Just as translating 12-equal or 19-equal material with an 81/80 comma pump requires a half-fret pitch shift, translating 22-equal material with a Triyo aka Porcupine comma pump does too. As does translating 19-equal material with a Zozo comma pump. The same rules apply.
The Bohlen-Pierce 13-EDT scale is a subset of 41-equal, so a direct translation is possible, but usually awkward to play. Another possibility is translating to one of the Octotonic (3L 3m 2s) scales, which have unequal steps, but avoid the 3 wolves of B-P (^5, v8 and M10).
Original compositions
Main article: Kite Guitar originals
Like translations, these are grouped by the creator. If you have originals, please create your own page and link to it!
Further materials
Kite Guitar explanation for non-microtonalists
Ratios and cents, just intonation and EDOs, and the how and why of the Kite Guitar
How to make a Kite Guitar
This page covers all options from simple DIY conversions to custom builds by professional luthiers.
- General design considerations
- Fret placement
- Fret markers
- DIY frets
- String gauges
- Saddle and nut compensation
- String spacing
- Resources (string vendors, saddle vendors, etc.)
- Cents table and frequency table
Extended range guitar
Sources for 7-string and 8-string guitars
Kite Guitar exercises and techniques
Various exercises and techniques by various teachers. The circle of 5ths, half-fret bends, etc.
Mathematical basis for the Kite Guitar
A "Kite-like" guitar can be tuned to edos 19, 22, 41, 60, 63, 85 and 104, as well as rank-2 Laquinyo/Magic.
Scales on the Kite Guitar
A theoretical exploration of 41-equal scales. The 5 categories are pentatonic, diatonic, semitonal, fretwise and microtonal.
Kite's thoughts on 41-equal note names and key signatures
How to name any note in any chord on any root in any key, using ups and downs. Suggested formats for key signatures.
41-equal chord names
How to name various triads and tetrads, even those not easily playable on the Kite guitar such as C~7.
KDF fret numbering
Avoid large numbers and tedious mental calculations by counting kites, dots and frets.
41edo lattices
Explores lattices and commas, aimed at composers.
Tuning a Kite Guitar to 31edo or 62edo
It's possible to tune a Kite guitar to quasi-62edo, with less than 1¢ error over most of the fretboard. Every other fret yields 31edo.
Brief history
The first true Kite guitar was made in April 2019 by Kite Giedraitis by adjusting the frets on his cable-tie guitar. He was directly inspired by Matthew Autry's experiments with skip-frettings. Matthew explored large edos like 72 and 130, but had never explored 41. Kite's May 2019 paper announcing the invention: The Kite Tuning (16 page pdf).
Unbeknownst to Kite, Robin Perry had independently invented the Kite guitar in November 2011. He made a "Kite-like" prototype in 60edo (see Mathematical Basis For The Kite Guitar) with frets at 4\60, 7\60, 10\60, etc. It was a 7-string lute-like instrument tuned in 380¢ 3rds, or sometimes an open tuning. In 2012 he proposed a fretting of every other step of 41edo (3\41, 5\41, 7\41, etc.), and modified his prototype to roughly approximate it by moving the bridge. Thus he was the first to conceive of the Kite guitar, if not build one. He announced his invention on facebook, but didn't pursue the matter, as he was not satisfied with the overall concept (source).
Others had come close to the Kite guitar, but either didn't use 41-edo, or had unequally spaced frets. See Graham Breed's Magic Guitar (2013) and Mason Green's Devadoot guitar (2016).
Other 41-equal instruments
The term "Kite" as in Kite guitar, Kite keyboard, Kite trumpet, etc., refers to skipping every other step of 41-edo, so that adjacent notes are 2\41 apart, and notes 1\41 away are less accessible. Thus Kite guitar is short for Kite-fretted guitar, Kite keyboard is short for Kite-keyed keyboard, etc.
41-edo keyboards
Kite-valved brass instruments
For a list of all xenwiki pages on the Kite Guitar, see Category: Kite Guitar.