Kite Guitar chord shapes (downmajor tuning)
See also: 41edo chord names
Overview
There are many chords on the Kite Guitar to explore, but the obvious place to start is with those of intervallic odd-limit 9 or less. These chords are mostly subsets of the 4:5:6:7:9 pentad or the 9:7:6:5:4 pentad. Thus most of these chords can be classified as either harmonic or subharmonic. Chords such as vM7, ^m7, vm7 and v6 are classified as stacked chords, because they are formed by stacking complimentary 3rds. Many chords fall outside these 3 categories.
Homonyms are to chords what modes are to scales. C6 and Am7 are homonyms (same notes, different root). In theory, every tetrad has 3 other homonyms, but in practice many are too implausible (e.g. Am7 = G6/9sus4no5). Most tetrads and pentads have at least one plausible homonym.
These tables list all chords of odd-limit 9, plus a few with downmajor 7ths that are odd-limit 15. The example chords are arbitrarily rooted on C. The chord shapes are written in tablature, using fret numbers. The root is placed arbitrarily on the 4th fret, even though C is not on the 4th fret. In these tables, the interval between open strings is always a downmajor 3rd. This makes the Kite guitar isomorphic, thus a tab like 4 6 3 5 can start on the 6th, 5th or 4th string, and of course any fret of that string. A skipped string is indicated by a period. Alternate fingerings are possible, especially for 2-finger and 3-finger chords.
Chords are named using ups and down notation, see the notation guide for edos 5-72. Briefly, an up or down in the chord name immediately after the root affects the 3rd, 6th, 7th and/or the 11th, but not the 5th, 9th or 13th. Thus Gv9 is G vB D vF A. Alterations are enclosed in parentheses, as in Cvm7(b5). Additions are set off with a comma (the punctuation mark, not the interval!). In general, the comma is spoken as "add", e.g. Cv,9 = "C down add-9" = C vE G D. Chord progressions are written as Cv7 - vEb^m6 - Fv7 or Iv7 - vbIII^m6 - IVv7.
Chord voicings are named using hi-lo notation, as hi3, lo5, etc.
In general, an odd-limit 15 chord has only one 15-limit interval, and most of the others are much lower odd-limit. For example, the downmajor seven chord has intervals of odd-limit 3, 3, 5, 5, 5 and 15. The many low-limit intervals serve as "glue" to hold together the chord, despite the one 15-limit interval. This is the rationale for focusing on odd-limit 15 chords here and not those of odd-limit 11 or 13, for those chords have multiple intervals of high odd-limit. But see below, at the very end of this section.
These tables are fairly exhaustive. Don't get overwhelmed! The most essential chords are in the first two tables (triads and seventh chords). Here's a printer-friendly chart to get you started, with and without fingerings:
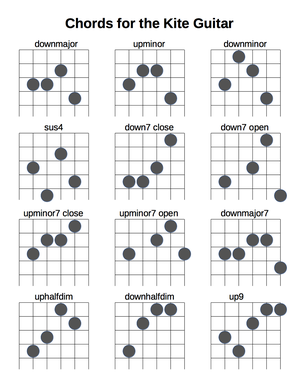

Triads
The names for the voicings are explained in the next section. Other voicings are possible; these are just the most convenient ones. The upmajor chord is a particularly dissonant triad. See "Innate-comma chords" below for augmented triads. Added ninths are shown in parentheses. Adding a major 9th (ratio 9/4, example note D) to the up or down triad increases the intervallic odd-limit only slightly if at all. The up chord is arguably improved by adding a 9th. The two sus chords have another homonym, the dom7sus4 chord, which is discussed below. The cryptic superscripted-circle symbol for diminished can be replaced with the far more intuitive and obvious lower-case d.
| Chord type → | Sus4 | Up or
upmajor (up add 9) |
Down or
downmajor (down add 9) |
Upminor | Downminor | Sus2 | Updim | Downdim |
|---|---|---|---|---|---|---|---|---|
| Example, with homonym | C4 = F2 | C^ (C^,9) | Cv (Cv,9) | C^m | Cvm | C2 = G4 | C^dim or C^d | Cvdim or Cvd |
| Example notes | C F G | C ^E G | C vE G | C ^Eb G | C vEb G | C D G | C ^Eb Gb | C vEb Gb |
| Ratio of the 3rd | P4 = 4/3 | ^M3 = 9/7 | VM3 = 5/4 | ^m3 = 6/5 | Vm3 = 7/6 | M2 = 9/8 | ^m3 = 6/5 | Vm3 = 7/6 |
| Ratio of the 5th | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 | D5 = 7/5 | D5 = 7/5 |
| close voicing R 3 5 8 (9) | ||||||||
| Frets | 4 6 3 5 | 4 5 3 5 (2) | 4 4 3 5 (2) | 4 3 3 5 | 4 2 3 5 | 4 1 3 5 | 4 3 1 5 | 4 2 1 5 |
| Suggested fingerings | 2 4 1 3 | 2 3 1 4 | 2 3 1 4
2 2 1 4 |
2 1 1 3 | 3 1 2 4 | 3 1 2 4 | 3 2 1 4 | 3 2 1 4 |
| open or hi3 voicing R 5 8 3 | ||||||||
| Frets | 4 . 3 5 7 | 4 . 3 5 6 | 4 . 3 5 5 | 4 . 3 5 4 | 4 . 3 5 3 | 4 . 3 5 2 | 4 . 1 5 4 | 4 . 1 5 3 |
| Suggested fingerings | 2 . 1 3 4 | 2 . 1 3 4 | 2 . 1 3 4
2 . 1 4 4 |
2 . 1 4 3 | 3 . 1 4 2 | 3 . 2 4 1 | 2 . 1 4 3 | 3 . 1 4 2 |
| hiR voicing 3 5 8 (9) (1st inversion) | ||||||||
| Frets | 5 2 4 | 4 2 4 (1) | 3 2 4 (1) | 2 2 4 | 1 2 4 | 0 2 4 | 2 0 4 | 1 0 4 |
| Suggested fingerings | 4 1 3 | 2 1 3 | 2 1 3 | 1 1 3 | 1 2 4 | 1 2 4 | 2 1 4 | 2 1 4 |
| addlo5 voicing 5 R 3 5 (2nd inversion) | ||||||||
| Frets | 2 4 6 3 | 2 4 5 3 | 2 4 4 3 | 2 4 3 3 | 2 4 2 3 | 2 4 1 3 | (difficult) | (difficult) |
| Suggested fingerings | 1 3 4 2 | 1 3 4 2 | 1 3 4 2 | 1 4 2 3
1 3 2 2 |
1 3 1 2 | 2 4 1 3 | ||
Seventh chords
It's generally impossible to voice 7th chords in 1st, 2nd or 3rd inversion close voicings, because the 7th usually occurs on the same string as the 8ve. One exception is the dom7sus4 chord. Its 7th shares a string with the 5th, so the 5th is generally omitted.
Since the usual inversions aren't possible in close voicings, the terminology changes. Voicings are named using hi-lo notation as close (root position, R 3 5 7), hi3 (3rd raised an 8ve), lo5 (5th lowered an 8ve), etc. The hi3lo5 voicing (5 R 7 3) and the hi35 voicing (R 7 3 5) both use all 6 strings, thus they are only sometimes possible. A hi37 voicing (R 5 3 7) requires 7 strings.
The upmajor7 chord C^M7 = C ^E G ^B is a possibility, but it's quite dissonant, with ^M7 = 27/14. See "Innate-comma chords" below for dim7 chords and yet more dom7 chords.
9ths are shown in parentheses. Adding a major 9th (ratio 9/4, example note D) to any of the first 4 tetrads increases the intervallic odd-limit only slightly if at all. The up-7 chord is arguably improved by adding a 9th. The no3, no5 and no7 (i.e. add9) versions of the ^9 and v9 chords are all 9-odd-limit chords.
11th chords include vM11 (4 4 3 3 2 0), v11 (4 4 3 1 2 0), and ^m11 (4 3 3 2 2 1). All these chords contain an offperfect 11th. Rather than 8/3, the vM11 and v11 chords have 21/8, and the ^m11 chord has 27/10. The mid-11th, ratio 11/4, is also available. However 4:5:6:7:9:11 is very difficult to play.
The wordy min7b5 and the illogical half-dim can be replaced with dim add7. The cryptic superscripted-circle-with-slash symbol becomes either ^d^7 or vdv7.
| Chord type → | Downmajor7
(downmajor9) |
Up7
(up9) |
Down7
(down9) |
Upminor7
(upminor9) |
Downminor7 | Updim up7 | Downdim
down7 |
Dom7sus4no5 |
|---|---|---|---|---|---|---|---|---|
| Example, with
homonym |
CvM7
(CvM9) |
C^7
(C^9) |
Cv7
(Cv9) |
C^m7 = ^Ebv6
(C^m9) |
Cvm7
= vEb^6 |
C^d^7
= ^Ebvm6 |
Cvdv7
= vEb^m6 |
C7sus4no5
= F4 = Bb2 |
| Example notes | C vE G vB | C ^E G ^Bb | C vE G vBb | C ^Eb G ^Bb | C vEb G vBb | C ^Eb Gb ^Bb | C vEb Gb vBb | C F Bb |
| Ratio of the 3rd | VM3 = 5/4 | ^M3 = 9/7 | VM3 = 5/4 | ^m3 = 6/5 | Vm3 = 7/6 | ^m3 = 6/5 | Vm3 = 7/6 | P4 = 4/3 |
| Ratio of the 5th | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 | D5 = 7/5 | D5 = 7/5 | ------ |
| Ratio of the 7th | VM7 =15/8 | ^m7 = 9/5 | Vm7 = 7/4 | ^m7 = 9/5 | Vm7 = 7/4 | ^m7 = 9/5 | Vm7 = 7/4 | M7 = 16/9 |
| close voicing R 3 5 7 (9) | ||||||||
| Frets | 4 4 3 3 (2) | 4 5 3 2 (2) | 4 4 3 1 (2) | 4 3 3 2 (2) | 4 2 3 1 | 4 3 1 2 | 4 2 1 1 | 4 6 8 |
| Suggested
fingerings |
3 4 2 2 (1)
3 3 2 2 (1) 1 1 1 1 (1) |
3 4 2 1 (1) | 3 4 2 1
4 4 3 1 (2) |
4 2 3 1 (1)
4 3 2 1 (1) 3 2 2 1 (1) |
4 2 3 1 | 4 3 1 2 | 4 2 1 1 | 1 3 4
1 2 4 |
| hi3 voicing R 5 7 3 | ||||||||
| Frets | 4 . 3 3 5 | 4 . 3 2 6 | 4 . 3 1 5 | 4 . 3 2 4 | 4 . 3 1 3 | 4 . 1 2 4 | 4 . 1 1 3 | (difficult) |
| Suggested
fingerings |
2 . 1 1 3 | 3 . 2 1 4 | 3 . 2 1 4 | 3 . 2 1 4
2 . 1 1 4 |
4 . 2 1 3 | 3 . 1 2 4 | 4 . 1 1 3 | |
| lo5 voicing 5 R 3 (5) 7 (9) | ||||||||
| Frets | 2 4 4 (3) 3 (2) | 2 4 5 (3) 2 (2) | 2 4 4 (3) 1 (2) | 2 4 3 (3) 2 (2) | 2 4 2 (3) 1 | (difficult) | (difficult) | (difficult) |
| Suggested
fingerings |
1 3 4 (2) 2 (1) | 1 3 4 (2) 1 (1) | 2 3 4 . 1
1 3 4 (2) 1 1 3 4 . 1 (2) |
1 4 3 . 2 (2)
1 3 2 (2) 1 (1) 1 4 3 (2) 1 (1) 1 4 2 (3) 1 (1) |
2 4 2 (3) 1 | |||
| lo7 voicing 7 R 4 5 | ||||||||
| Frets | (N/A) | (N/A) | (N/A) | (N/A) | (N/A) | (N/A) | (N/A) | 7 4 6 8 |
| Suggested
fingerings |
3 1 2 4 | |||||||
Flat-nine chords are possible. The plain minor 9th is 21/10, which is the sum of 7/5 and 3/2, thus a m9 works with either a perfect or diminished 5th. Examples:
- the upminor-7 flat-9 chord = C^m7b9 = C ^Eb G ^Bb Db = 4 3 3 2 0
- the upminor-7 flat-5 flat-9 chord = C^m7(b5)b9 = C ^Eb Gb ^Bb Db = 4 3 1 2 0
- the downminor-7 flat-9 chord = Cvm7b9 = C vEb G vBb Db = 4 2 3 1 0
- the downminor-7 flat-5 flat-9 chord = Cvm7(b5)b9 = C vEb Gb vBb Db = 4 2 1 1 0
The upminor 9th (15/7) is also possible, but hard to play, Example: the downmajor-7 upflat-9 chord = CvM7^b9 = C vE G vB ^Db. Note that ^Db is enharmonically equivalent to C#, the augmented 8ve. Thus this chord's homonym is vE^m6/C.
Sixth chords
Every 6th chord has a 7th chord homonym, and vice versa. But a 7th chord with some sort of major 7th doesn't "flip" to a 6th chord as easily, because the 6th would be some sort of minor 6th, which is rare.
Sixth chords are hard to voice. A close voicing in root position is generally impossible, because the 6th occurs on the same string as the 5th. One solution is to play a riff that alternates between the 5th and the 6th (3/6 in the tab indicates alternating between the 3rd and 6th fret). Another is to omit the 5th, but then the chord can be mistaken for a triad in 1st inversion. It helps to double the root at the octave, i.e. play R 3 6 8 not R 3 6. Another voicing is the lo6 (6 R 3 5) i.e. the 3rd inversion. But this is the same as the close voicing of its 7th chord homonym, and again the chord can be mistaken. A non-ambiguous voicing is lo5 (5 R 3 6), but it can be a difficult stretch. Also the 9th from the 5th to the 6th is usually not a plain 9th, and can be dissonant. The best voicing is hi35 (R 6 3 5 or R 6 8 3 5), but it spans 6 strings, and isn't possible for all chords unless you have 8 strings. Other possibilities are hi36 (R 5 3 6), hi5 (R 3 6 5 or R 3 6 8 5) and hi6add8 (R 3 5 8 6).
The up-6 chord is particularly dissonant, unless voiced as its homonym, the vm7 chord.
Adding a major 9th (ratio 9/4) to any of these chords will make an offperfect 4th with the 6th. A 9th that is a P4 above the 6th (^M9 or vM9) will clash with the 5th. It can be safely added if the 5th is omitted, but then the chord becomes ambiguous. Cv6v9no5 is the same as vD^9no3 (or vD^m9no3). C^6^9no5 is ^Dv9no3. C^m6^9no5 and Cvm6v9no5 both have an awkward interval from the 3rd up to the 9th: a M7 = 40/21.
Adding an 11th (ratio 8/3) to either the ^m6 or the vm6 chord won't increase the intervallic odd-limit above 9. But a Cvm6,11 chord is the same as an Fv9 chord, and every easy fingering puts the F in the bass, so it's hardly a distinct chord. Adding an 11th to a Cv6 chord makes Cv6,11, which is an FvM9 chord. Again, every easy fingering has F in the bass, and Cv6,11 isn't a distinct chord. The ^m6,11 chord can be voiced hi35lo11, so that the 11th is a 4th. This is equivalent to a lo5 voicing of its homonym the ^9 chord.
| Chord type → | Up6 or
upmajor6 |
Down6 or
downmajor6 |
Upminor6
(upminor6 add11) |
Downminor6 |
|---|---|---|---|---|
| Example, with homonym(s) | C^6 = ^Avm7 | Cv6 = vA^m7 | C^m6 = ^Avdv7
(C^m6,11 = F^9) |
Cvm6 = vA^d^7
= Fv9noR |
| Example notes | C ^E G ^A | C vE G vA | C ^Eb G ^A | C vEb G vA |
| Ratio of the 3rd | ^M3 = 9/7 | VM3 = 5/4 | ^m3 = 6/5 | Vm3 = 7/6 |
| Ratio of the 5th | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 | P5 = 3/2 |
| Ratio of the 6th | ^M6 = 12/7 | VM6 = 5/3 | ^M6 = 12/7 | VM6 = 5/3 |
| close voicing for riffing R 3 5/6 (8) | ||||
| Frets | 4 5 3/7 | 4 4 3/6 | 4 3 3/7 (5) | 4 2 3/6 |
| Suggested fingerings | 2 3 1/4 | 2 3 1/4 | 2 1 1/4 (3) | 3 1 2/4 |
| close no5add8 voicing R 3 6 8 | ||||
| Homonyms | C^6no5 = ^Avm | Cv6no5 = vA^m | C^m6no5 = ^Avd | Cvm6no5 = vA^d |
| Frets | 4 5 7 5 | 4 4 6 5 | 4 3 7 5 | 4 2 6 5 |
| Suggested fingerings | 1 2 4 3 | 1 1 3 2 | 2 1 4 3 | 2 1 4 3 |
| lo6 voicing 6 R 3 5 (11) | ||||
| Frets | 6 4 5 3 | 5 4 4 3 | 6 4 3 3 . (7) | 5 4 2 3 |
| Suggested fingerings | 4 2 3 1 | 4 2 3 1 | 4 2 1 1
3 2 1 1 . (4) |
4 3 1 2 |
| lo5 voicing 5 R 3 6 | ||||
| Frets | 2 4 5 7 | 2 4 4 6 | 2 4 3 7 | 2 4 2 6 |
| Suggested fingerings | 1 2 3 4 | 1 2 3 4 | 1 3 2 4 | 1 3 1 4 |
| hi35 voicing R (4) 6 (8) 3 5 | ||||
| Frets | 4 . 7 . 6 4 | 4 . 6 (5) 5 4 | 4 (6) 7 (5) 4 4 | 4 . 6 (5) 3 4 |
| Suggested fingerings | 1 . 4 . 3 2
1 . 4 . 3 1 |
1 . 4 . 3 2
1 . 4 (2) 3 1 |
1 (3) 4 (2) 1 1 | T . 4 (3) 1 2
(T = thumb) |
If you play a 7th chord in close root position on the upper 4 strings, you can drop the 3rd of the chord down an octave to get a hi35 voicing of the corresponding 6th chord.
- x x A x E ^G ^C (clearly A^m7)
- x x A ^C E ^G x (ambiguous but slightly more A^m7)
- ^C x A x E ^G x (clearly ^C6)
Innate-comma chords
Various innate-Ruyoyo chords
We've covered every chord that maps to a JI chord of intervallic odd-limit 9. However there are many Kite guitar chords that don't, although their individual intervals do. These chords are called innate-comma chords aka essentially tempered chords. Such chords often have a mysterious sound. Almost every easily reachable interval on the fretboard is odd-limit 9. The only exceptions are ~4, ~5, vM7, ^M7, vm9 and ^m9. Thus the majority of random Kite guitar chord shapes are intervallic odd-limit 9.
For example, the downadd7no5 chord has 5/4 and 16/9. The interval from 5/4 up to 16/9 is 64/45. But because 41edo tempers out the Ruyoyo comma of only 8¢, 64/45 is equivalent to 10/7. The hi3 voicing inverts this into an even smoother 7/5. This dom7 chord is often appropriate for translating 12-edo's V7 -- I cadence: relaxed but not too relaxed. Adding the 5th creates a plain minor 3rd interval with the 7th. If the m3 is interpreted as 32/27, this increases the odd limit to 27. But if interpreted as 13/11, the odd limit is only 13.
The sus4downmajor7 chord (odd-limit 15) also has an innate Ruyoyo comma. The chord is quite striking in close voicing. The interval from 4/3 up to 15/8 is 45/32, equivalent to 7/5. The homonym of C4vM7 = C F G vB is the sus2addb5 chord F2b5 = F G Cb C. In 41-edo, Cb is enharmonically equivalent to vB. In chord names, "(b5)" means alter the 5th by flattening it, but "b5" means add a flat 5th alongside the perfect 5th.
The down7flat5 chord (odd-limit 9) is also innate-ruyoyo. The interval from 5/4 up to 7/5 is 28/25, equivalent to 9/8. The homonym of Cv7(b5) is the Gb downadd7upflat5 chord Gbv,7(^b5) = Gb vBb ^Dbb Fb. Enharmonic equivalences: ^Dbb = C, Fb = vE, and upflat 5th = aug 4th = 10/7.
All three of these chords contain the chord shape 4 1 1. This 3-note "nugget" implies the Ruyoyo comma: 9/8 plus 5/4 equals 7/5. By itself, it's the v,7no5 chord in lo7 voicing. The v7(b5) chord in close voicing (4 4 1 1) also contains the octave inverse of this nugget, 4 4 1. By itself, this inverse nugget makes Cv(b5) = C vE Gb (odd-limit 9). Beware, "C-down flat-5" = Cv(b5) sounds much like "C downflat-5" = C(vb5) = C E vGb = C E ^^F = 8:10:11. To avoid ambiguity, one could say "C-downmajor flat-5".
The downaddflat5 chord Cv,b5 (odd-limit 15) has both a perfect and a diminished 5th. This chord is best voiced lo5. In other voicings, the two 5ths are on the same string, and one must play a riff that alternates between the two (indicated as 1/3 in the tab, 1st and 3rd fret).
When the added b5 is voiced an 8ve higher, it becomes a v#11, and suggests the downmajor7downsharp11 and downmajor9downsharp11 chords (both odd-limit 15). No need to omit the 3rd, it makes a pleasant M9 = 9/4 with the 11th.
| Chord type → | Downadd7no5 | Downmaj7sus4 | Downmaj7flat5 | Down7flat5 | Down flat5 | Downaddflat5 | Downmaj9down#11 |
|---|---|---|---|---|---|---|---|
| Example w homonym | Cv,7no5 = Bb2(b5) | C4vM7 = F2b5 | CvM7(b5) = vE2^m6 | Cv7(b5) = Gbv,7(^b5) | Cv(b5) | Cv,b5 | CvM9v#11 |
| Example notes | C vE Bb | C F G vB | C vE Gb vB | C vE Gb vBb | C vE Gb | C vE Gb G | C vE G vB D vF# |
| Ratio of the 3rd | VM3 = 5/4 | P4 = 4/3 | VM3 = 5/4 | VM3 = 5/4 | VM3 = 5/4 | VM3 = 5/4 | VM3 = 5/4 |
| Ratio of the 5th | ------ | P5 = 3/2 | D5 = 7/5 | D5 = 7/5 | D5 = 7/5 | P5 = 3/2 | P5 = 3/2 |
| Ratio of the 7th | M7 = 16/9 | VM7 = 15/8 | VM7 = 15/8 | Vm7 = 7/4 | ------ | ------ | VM7 =15/8 |
| Other | ------ | ------ | ------ | ------ | ------ | D5 = 7/5 | V#11 = b12 = 14/5 |
| close voicing R 3 5 7 (8) | |||||||
| Frets | 4 4 8 (5) (5) (4) | 4 6 3 3 | 4 4 1 3 | 4 4 1 1 | 4 4 1 (5) | 4 4 1/3 | 4 4 3 3 2 2 |
| Suggested fingerings | 1 1 4 (2) (2) (1) | 2 4 1 1 | 3 4 1 2 | 3 4 1 1 | 3 4 1 2 3 1 (4) |
3 4 1/2 | 3 4 2 2 1 1 |
| hi3 voicing R 5 7 (8) 3 | |||||||
| Frets | 4 . 8 (5) 5 | 4 . 3 3 7 | 4 . 1 3 5 | 4 . 1 1 5 | 4 . 1 (5) 5 | 4 . 1/3 (5) 5 | 4 . 3 3 5 2 (no 9th) |
| Suggested fingerings | 1 . 4 . 2 1 . 4 (1) 1 |
2 . 1 1 4 | 3 . 1 2 4 | 3 . 1 1 4 | 2 . 1 (3) 4 | 3 . 1/2 . 4 2 . 1/3 (3) 4 |
2 . 3 3 4 1 |
| lo5 voicing 5 R 3 7 | |||||||
| Frets | (N/A) | (difficult) | 0 4 4 . 3 | 0 4 4 . 1 | (difficult) | 2 4 4 1 | 2 4 4 . 3 2 2 |
| Suggested fingerings | 1 3 4 . 2 | 1 3 4 . 2 | 2 3 4 1 | 1 3 4 . 2 1 1 | |||
| lo7 voicing 7 R 3 (7) | |||||||
| Frets | 7 4 4 (8) | (N/A) | (N/A) | (N/A) | (N/A) | (N/A) | (N/A) |
| Suggested fingerings | 3 1 1 (4) | ||||||
Augmented Chords
The Ruyoyo comma implies an augmented chord because it equates the octave with 5/4 plus 5/4 plus 9/7. In 12-edo, the aug chord is symmetrical, and it is its own homonym. But in 41edo, it's asymmetrical. Its homonyms are also augmented chords, but of a different type. Thus there are three basic augmented chords: upaug, downaug and down-halfaug. In the last chord, the 5th is spelled as vv#5 rather than ^^5 so that the interval from the 3rd to the 5th is spelled as vM3 not ^3m3. An alternative name for down-halfaug is down-dudsharp5 (dud is short for double-down).
There is another trio of aug chords: up-halfaug, upminor-halfaug and up-dupaug, all homonyms. Dup is short for double-up. Their innate comma is the Zozoyo comma, which equates the octave with 9/7 plus 9/7 plus 6/5. Thus one 3rd is quite smaller than the other two. Only the uphalfaug is clearly an augmented chord. Since the 3rd is upped, the chord's 5th is spelled as ^^5 not vv#5. The upminor-halfaug chord's lowest 3rd is this small 3rd, and it really can't be called an augmented chord. The up-dupaug chord has ^^#5, a dupaugmented 5th. This is equivalent to a downmajor 6th, and again, it's debatable if this is really an augmented chord. In close voicing it uses every 3rd note of the Bohlen–Pierce scale.
All six chords are odd-limit 9. Another possible aug chord is odd-limit 11. Unlike the others, it has no innate comma. 7:9:11 = up-downsharp5 = C^(v#5) = C ^E vG#. Unfortunately it's very difficult to finger. Using an open string, it's 5 6 x 0. But see Kite Guitar Exercises and Techniques by Kite Giedraitis#Primes 11 and 13 for an alternative way to play this chord, as well as 8:10:13 = down-upsharp5 = Cv(^#5) = C vE ^G#.
The cryptic plus-sign symbol for augmented can be replaced with the far more intuitive and obvious lower-case a.
| Chord type → | Upaug | Downaug | Downhalfaug | Uphalfaug | Upminor-halfaug | Up-dupaug |
|---|---|---|---|---|---|---|
| Example with homonyms | C^a = ^Ev(vv#5)
= ^Abva |
Cva = vE^a
= ^Abv(vv#5) |
Cv(vv#5) = vEva
= vAb^a |
C^(^^5) = ^E^m(^^5)
= vAb^(^^#5) |
C^m(^^5) = ^Eb^(^^#5)
= vAb^(^^5) |
C^(^^#5) = ^E^(^^5)
= vA^m(^^5) |
| Example notes | C ^E G# | C vE G# | C vE vvG# | C ^E ^^G | C ^Eb ^^G | C ^E ^^G# |
| 3rd | ^M3 = 9/7 | VM3 = 5/4 | VM3 = 5/4 | ^M3 = 9/7 | ^m3 = 6/5 | ^M3 = 9/7 |
| 5th | A5 = ^m6 = 8/5 | A5 = ^m6 = 8/5 | VvA5 = vm6 = 14/9 | ^^5 = vm6 = 14/9 | ^^5 = vm6 = 14/9 | ^^A5 = vM6 = 5/3 |
| close voicing R 3 5 (8) | ||||||
| Frets | 4 5 5 (5) | 4 4 5 (5) | 4 4 4 (5) | 4 5 4 (5) | 4 3 4 (5) | 4 5 6 (5) |
| Fingerings | 1 2 2 (2) | 1 1 2 (2) | 1 1 1 (2) | 1 3 2 (4) | 2 1 3 (4) | 1 2 4 (3) |
| hi3 voicing R 5 (8) 3 | ||||||
| Frets | 4 . 5 (5) 6 | 4 . 5 (5) 5 | 4 . 4 (5) 5 | 4 . 4 (5) 6 | 4 . 4 (5) 4 | 4 . 6 (5) 6 |
| Fingerings | 1 . 2 (2) 3 | 1 . 2 (2) 2 | 1 . 1 (2) 2 | 1 . 1 (2) 3 | 1 . 2 (4) 3 | 1 . 3 (2) 4 |
| hiR voicing 3 5 8 (3) (1st inversion) | ||||||
| See v(vv#5) | See ^a | See va | See ^m(^^5) | See ^(^^#5) | See ^(^^5) | |
| lo5 voicing 5 R 3 (5) (2nd inversion) | ||||||
| See va | See v(vv#5) | See ^a | See ^(^^#5) | See ^(^^5) | See ^m(^^5) | |
Diminished Chords
The updim7 and downdim7 chords are formed from stacked 6/5's and 7/6's, alternating to make 7/5's. The 7ths are rather dissonant. The updim7 chord has an innate Ruyoyo comma which equates its ^d7 = 42/25 to a M6 = 27/16. The downdim7 chord has an innate Thuzozogu comma which equates vd7 = 49/30 with ~6 = 13/8. Thus its odd-limit and prime-limit are both 13.
In 12-edo, the dim7 chord is symmetrical, and is its own homonym. But in 41-edo, it has homonyms. The most plausible one has the 3rd becoming the new root to make a 6th chord. This is a chord with a minor 3rd, a dim 5th and a major 6th. Such a chord in 12edo is identical to a dim7 chord, but in 41edo it isn't. Extrapolating from the terms maj6 and min6 gives us its name, a dim6 chord. To convert an updim7 chord to an updim6 chord (or downdim7 to downdim6), raise the 7th by one edostep. Thus C updim7 is only one edostep away from C updim6, which is equivalent to ^A downdim7 chord. Therefore C updim7 and ^A downdim7 are fuzzy homonyms. As are ^Eb downdim6 and ^A downdim7. Fuzzy homonyms are rare. They only occur when a chord spans 5 or 6 frets, as these do.
To avoid negative fret numbers, the chords in the table start on the 6th fret. As with the triads, the cryptic superscripted-circle symbol for diminished can be replaced with the far more intuitive and obvious lower-case d.
| Chord type → | Updim7 | Downdim6 | Downdim7 | Updim6 |
|---|---|---|---|---|
| Example with homonym | C^d7 = ^Ebvd6 | Cvd6 = vA^d7 | Cvd7 = vEb^d6 | C^d6 = ^Avd7 |
| Example notes | C ^Eb Gb ^Bbb | C vEb Gb vA | C vEb Gb vBbb | C ^Eb Gb ^A |
| 3rd | ^m3 = 6/5 | Vm3 = 7/6 | Vm3 = 7/6 | ^m3 = 6/5 |
| 5th | D5 = 7/5 | D5 = 7/5 | D5 = 7/5 | D5 = 7/5 |
| 6th or 7th | ^d7 = M6 = 27/16 | VM6 = 5/3 | Vd7 = ~6 = 13/8 | ^M6 = 12/7 |
| close voicing R 3 5 7 or R 3 5/6 | ||||
| Frets | 6 5 3 2 | 6 4 3/8 | 6 4 3 1 | 6 5 3/9 |
| Fingerings | 4 3 2 1 | 3 2 1/4 | 4 3 2 1 | 3 2 1/4 |
| hi3 voicing R 5 7 3 | ||||
| Frets | 6 . 3 2 6 | (N/A) | 6 . 3 1 5 | (N/A) |
| Fingerings | 3 . 2 1 4 | 3 . 2 1 4 | ||
| hi35 voicing R 6 (8) 3 5 | ||||
| Frets | (difficult) | 4 . 6 (5) 3 2 | (difficult) | 3 . 6 (4) 3 1 |
| Fingerings | T . 4 (3) 2 1 | T . 4 (3) 2 1 | ||
See also Modulation via Dim7 Chords from "Kite Guitar Exercises and Techniques by Kite Giedraitis".
Mid-5th Chords
At the beginning of this article, chords of prime-limit 11 or 13 were dismissed because "those chords have multiple intervals of high odd-limit." But when innate-comma chords are allowed, this no longer holds true. For example, the mid-5th can be interpreted as either 16/11 or 13/9. Each of the following chords contain this interval, but all the other intervals in the chord are at most odd-limit 5, 7 or 9, depending on the chord. The one exception is the vM7(~5) chord, odd-limit 15.
| Mid-5th chord | Example | Notes | Frets | Homonym |
|---|---|---|---|---|
| Downminor mid-5 | Cvm(~5) | C vEb vvG | 4 2 2 | |
| Downminor-7 mid-5 | Cvm7(~5) | C vEb vvG vBb | 4 2 2 1 or 4 . 2 1 3 | VEbv^6 |
| Down up-6 | Cv^6 | C vE G ^A | 4 . 7 (5) 5 4 | ^Avm7(~5) |
| Upminor mid-5 | C^m(~5) | C ^Eb ^^Gb | 4 3 2 | |
| Upminor-7 mid-5 | C^m7(~5) | C ^Eb ^^Gb ^Bb | 4 3 2 2 or 4 . 2 2 4 | ^Eb^mv6 |
| Upminor down-6 | C^mv6 | C ^Eb G vA | 4 . 6 (5) 4 4 | VA^m7(~5) |
| Downmajor mid-5 | Cv(~5) | C vE vvG | 4 4 2 | |
| Downmajor-7 mid-5 | CvM7(~5) | C vE vvG vB | 4 4 2 3 or 4 . 2 3 5 |
Note that the mid-5th is spelled as a dupdim 5th from the chord root (^^Gb) if the 3rd is upped, but as a dud 5th (vvG) if the 3rd is downed. This avoids the interval from the 3rd to the 5th being spelled with a trup or trud (triple-up or triple-down).
The most important chord with a mid 5th is the downup7 chord. When translating pre-20th-century music to the Kite Guitar, the 7-limit up7 and down7 chords often sound inappropriate. The two best 5-limit translations of the dom7 chord are the downadd7 chord and the downup7 chord. The latter is used in Kite's Greensleeves translation. The mid-5th appears as the interval from the 3rd up to the 7th. In a 5-limit context it is 36/25. It's equated to 16/11 by the Luyoyo comma, and to 13/9 by the Thoyoyo comma.
| Chord type → | Downup7 or down9up7 |
|---|---|
| Example | Cv^7 or Cv9(^7) |
| Example notes | C vE G ^Bb (D) |
| Ratio of the 3rd | VM3 = 5/4 |
| Ratio of the 5th | P5 = 3/2 |
| Ratio of the 7th | ^m7 = 9/5 |
| Ratio of the 9th | (M9 = 9/4) |
| close voicing R 3 5 7 (9) | |
| Frets | 4 4 3 2 (2) |
| Suggested fingerings | 3 4 2 1 (1) |
| hi3 voicing R 5 7 3 | |
| Frets | 4 . 3 2 5 |
| Suggested fingerings | 3 . 2 1 4 |
| addlo5 voicing 5 R 3 5 7 (9) | |
| Frets | 2 4 4 3 2 (2) |
| Suggested fingerings | 1 3 3 2 1 (1) |
| noRaddlo7 voicing 7 3 5 7 | |
| Frets | 1 4 3 2 |
| Suggested fingerings | 1 4 3 2 |
More innate-comma chords
All these chords use commas that are tempered out in 41-edo:
Ruyoyo Marvel chords
Zozoyo Sensamagic chords
Lulu Rastmic chords
Lozoyo Keenanismic chords
Saluzo Pentacircle chords
Luzozogu Werckismic chords
Lururuyo Swetismic chords
Ruyoyo & Lozoyo Undecimal marvel chords
Lulu & Luzozogu Jove chords
Ruyoyo & Luzozogu Prodigy chords
Latrizo & Ruyoyo & Lozoyo Miracle chords
Luyoyo & Lozoyo Magical seventh chord
Parallels with 12-edo Jazz Guitar
Jazz guitarists often play 4 or 5 note chords that are movable, i.e. don't use open strings. A root-6 chord (root on the 6th string) often has a R-5-7-3-x-x or R-5-7-3-5-x voicing. For example, A7 might be voiced 57565x, Am7b5 might be 5655xx, etc. A root-5 chord might be voiced x-R-5-7-3-x.
On a 12edo guitar, a root-5 chord is a different shape than a root-6 chord, whereas on a Kite guitar, the shape is the same. Thus the terms root-5 and root-6 are less useful on the Kite guitar. But a very useful concept when arranging for a 6-string Kite guitar is tonic-4 vs. tonic-5 vs. tonic-6. This indicates which string the tonic appears on. For example, Kite's translation of "I Will Survive" in D is tonic-5, and his translation in ^Bb is tonic-6. On a 6-string, certain bass lines require the tonic to appear on certain strings. In 12-edo, the same concept applies, but tonic-4 is rare.
12-edo major thirds tuning
In the early 1960's, jazz guitarist Ralph Patt adopted an all-major-3rds tuning. He said it "makes the hard things easy and the easy things hard." Because of the reduced range, he used first a 7-string guitar, and later an 8-string guitar. He placed the dots on every other fret.
The chord shapes are very similar to the Kite guitar, see RalphPatt.com/Tune/Chords.html. After learning the Kite guitar, playing a 12-edo guitar tuned in 3rds is a very odd experience! From his website:
"Disadvantage of the major third tuning.
"It's not easy to play simple folk chords. They are quite difficult to play with this tuning. If all you want to do with the guitar is sing folk tunes, don't try this.
"Much of the classical guitar literature becomes difficult or impossible to play because of frequent use of open D and A strings. However, I found Bach and early lute music easier to play with this tuning. Jim DiSerio made my eight string classical guitar with a capo on the low Ab string, bringing it up to an A without affecting the tuning. That solved the problem of the "open" A string."
See also: