Dave Keenan & Douglas Blumeyer's guide to RTT/Tuning fundamentals
This is article 3 of 9 in Dave Keenan & Douglas Blumeyer's guide to RTT, or "D&D's guide" for short. In this article, we'll be explaining fundamental concepts behind the various schemes that have been proposed for tuning temperaments. Our explanations here will not assume much prior mathematical knowledge.
A tuning, in general xenharmonics, is simply a set of pitches for making music. This is similar to a scale, but without necessarily being a melodic sequence; a tuning may contain several scales. In regular temperament theory (RTT), however, tuning has a specialized meaning as the exact number of cents for each generator of a regular temperament, such as the octave and fifth of the typical form of the quarter-comma tuning of meantone temperament (it can also refer to a single such generator, as in "what is the tuning of quarter-comma meantone's fifth?"). This RTT meaning of "tuning" is slightly different from the general xenharmonic meaning of "tuning", because generator sizes alone do not completely specify a pitch set; we still have to decide which pitches to generate with these generators.
If you already know which tuning schemes you prefer and why, our RTT library in Wolfram Language supports computing them (as well as many other tuning schemes whose traits are logical extensions or recombinations of the previously identified schemes' traits), and it can be run for free in your web browser.
Douglas's introduction to regular temperament tuning
If you've been around RTT much, you've probably encountered some of its many named tuning schemes. Perhaps you've read Paul Erlich's seminal paper A Middle Path, which—among other major contributions to the field—introduced an important tuning scheme he called "TOP". Or perhaps you've used Graham Breed's groundbreaking web app [1], which lets one explore the wide world of regular temperaments, providing their "TE" and "POTE" tunings along the way. Or perhaps you've browsed the Xenharmonic wiki, and encountered temperaments whose info boxes include their "CTE" tuning or still others.
When I (Douglas) initially set out to teach myself about RTT tuning, it seemed like the best place to start was to figure out the motivations for these tuning schemes, as well as how to compute them. Dave later told me that I had gone about the whole endeavor backwards. I had jumped into the deep end before learning to swim (in this metaphor, I suppose, Dave would be the lifeguard who saved me from drowning).
At that time, not much had been written about the fundamentals of tuning methodology (at least not much had been written in a centralized place; there's certainly tons of information littered about on the Yahoo! Groups tuning lists and Facebook). In lieu of such materials, what I probably should have done is just sat down with a temperament or three and got my feet wet by trying to tune it myself, discovering the most basic problems of tuning directly, at my own pace and in my own way.
This is what folks like Paul, Graham, and Dave had to do in the earlier days of RTT. No one had been there yet. No papers or wiki pages had already been written about the sorts of advanced solutions as they would eventually come to develop, building up to them gradually, tinkering with tuning ideas over decades. I should have started at the beginning like they did—with the simple and obvious ideas like damage, target-intervals, and optimization—and worked my way up to those intermediate concepts like "TOP and "POTE" tuning schemes. But I didn't. I got distracted by the tricky stuff too early on, and got myself badly lost in the process.
And so Dave and I have written this article to help spare other beginners from a fate similar to the one that befell me. This article is meant to fill that aforementioned void of materials about the fundamentals of tuning, the stuff that was perhaps taken for granted by the RTT tuning pioneers once they'd reached the point of publishing their big theoretical achievements. If you consider yourself more of a practical musician than a theoretical one, these fundamentals are the most important things to learn. Those generalizable tuning schemes that theorists have given names have great value, such as for being relatively easy for computers to calculate, and for consistently and reasonably documenting temperaments' tunings, but they are not necessarily the tunings that you'll actually most want to use in your next piece of music. By the end of this article, you'll know about the different tuning effects you might care about, enough to know what to ask a computer for to get the generator tunings you want.
And if you're anything like I was when I was beginning to learn about regular temperament generators, while you are keen to learn how to find the optimum tunings for generators (such as this article and the rest of the series are primarily concerned with), you may also be keen to learn how to find good choices of which JI interval(s) to think of each generator as representing. In that case, what you are looking for is called a generator detempering, so please check that out. I would also like to impress upon you that generator detemperings are very different from and should not be confused with optimum generator tunings; it took Dave quite some time and effort to disabuse me of this conflation.
Initial definitions
Before digging into anything in detail, let's first define seven core concepts: tuning itself, damage, error, weight, target-intervals, held-intervals, and optimization.
Tuning
A common point of confusion among newcomers to RTT is the difference between tuning and temperament. So, let's clear that distinction up right away.
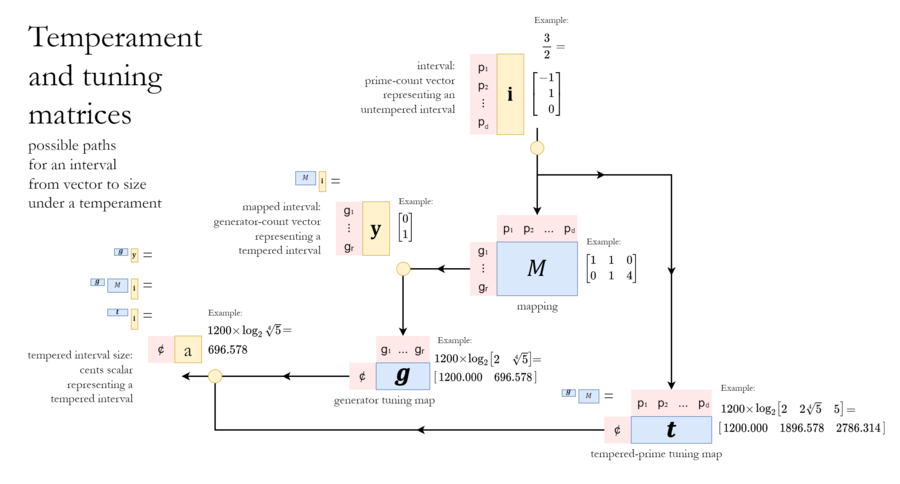
A regular temperament (henceforth simply "temperament") is not a finalized pitch system. It is only an abstract set of rules that a pitch system needs to follow. A temperament merely describes one way to approximate prime harmonics by using a smaller set of generating intervals, and it can be encapsulated in its entirety by a matrix of integers such as the following:
[math]\displaystyle{ \left[ \begin{matrix} 1 & 1 & 0 \\ 0 & 1 & 4 \\ \end{matrix} \right] }[/math]
In this case, the temperament tells us—one column at a time—that we reach prime 2 using 1 of the first generator, prime 3 using 1 each of the two generators, and prime 5 using 4 of the second generator. You may recognize this as the mapping for meantone temperament, which is an important historical temperament.
As we can see from the above example, temperaments do not make any specifications about the sizes of their generators. With a bit of training, one can deduce from the six numbers of this matrix that the first generator should be around an octave in size, and that the second generator should be around a perfect fifth in size—that is, assuming that we want this temperament to closely approximate these three prime harmonics 2, 3, and 5. But the exact sizes of these generators are left as an open question; no cents values are in sight here.
For one classic example of a tuning of meantone, consider quarter-comma tuning. Here, the octave is left pure, and the ~3/2 is set to [math]\displaystyle{ \small{696.578} \, \mathsf{¢} }[/math].[note 1] Another classic example of a meantone tuning would be fifth-comma, where the octave is also left pure, but the ~3/2 is instead set to [math]\displaystyle{ \small{697.654} \, \mathsf{¢} }[/math]. And if you read Paul Erlich's early RTT paper A Middle Path, he'll suggest that you temper your octaves (please!)[note 2] and for meantone, then, to tune your octave to [math]\displaystyle{ \small{1201.699} \, \mathsf{¢} }[/math] and your fifth to [math]\displaystyle{ \small{697.564} \, \mathsf{¢} }[/math]. So any piece of music that wishes to specify both its temperament as well as its tuning could provide the temperament information in the form of a matrix of integers such as featured above (or perhaps the temperament's name, if it is well-known enough), followed by its tuning information in the form of a list of generator tunings (in units of cents per generator) such as those noted here, which we'd call a generator tuning map. Here's how the three tunings we mentioned in this paragraph look set next to the temperament:
[math]\displaystyle{ \begin{array} {c} \text{tuning:} \\ \text{quarter-comma} \\ \left[ \begin{matrix} 1200.000 & 696.578 \end{matrix} \right] \end{array} \begin{array} {c} \text{temperament:} \\ \text{meantone} \\ \left[ \begin{matrix} 1 & 1 & 0 \\ 0 & 1 & 4 \\ \end{matrix} \right] \end{array} }[/math]
[math]\displaystyle{ \begin{array} {c} \text{tuning:} \\ \text{fifth-comma} \\ \left[ \begin{matrix} 1200.000 & 697.654 \end{matrix} \right] \end{array} \begin{array} {c} \text{temperament:} \\ \text{meantone} \\ \left[ \begin{matrix} 1 & 1 & 0 \\ 0 & 1 & 4 \\ \end{matrix} \right] \end{array} }[/math]
[math]\displaystyle{ \begin{array} {c} \text{tuning:} \\ \text{Middle Path} \\ \left[ \begin{matrix} 1201.699 & 697.564 \end{matrix} \right] \end{array} \begin{array} {c} \text{temperament:} \\ \text{meantone} \\ \left[ \begin{matrix} 1 & 1 & 0 \\ 0 & 1 & 4 \\ \end{matrix} \right] \end{array} }[/math]
This open-endedness of tuning is not a bug in the design of temperaments, by the way. It's definitely a feature. Being able to speak about harmonic structure at the level of abstraction that temperaments provide for us is certainly valuable. (And we should note here that even after choosing a temperament's tuning, you're still in the realm of abstraction; you won't have a fully-formed pitch system ready to make music with until you choose how many pitches and which pitches exactly to generate with your generators!)
But why should we care about the tuning of a regular temperament, or—said another way—what makes some generator tunings better than others? The plain answer to this question is: some sound better. And while there may be no universal best tuning for each temperament, we could at least make cases for certain types of music—or specific pieces of music, even—sounding better in one tuning over another.
Now, an answer like that suggests that RTT tuning could be done by ear. Well, it certainly can. And for some people, that might be totally sufficient. But other people will seek a more objective answer to the question of how to tune their temperament. For people of the latter type: we hope you will get a lot out of this article.
And perhaps this goes without saying, but another important reason to develop objective and generalized schemes for tuning temperaments is to be able to empower synths and other microtonal software with intelligent default behavior. Computers aren't so good with the whole tuning-by-ear thing. (Though to help this article age a bit more gracefully, we should say they are getting better at it every day!)
So to tie up this temperament vs. tuning issue[note 3], maybe we could get away with this analogy: if temperament is like a color scheme, then tuning is like the exact hex values of your colors. Or maybe we could think of tuning as the fine tuning of a temperament. Either way, tuning temperaments is a good mix of science and art—like any other component of music—and we hope you'll find it as interesting to tinker with as we have.
Damage, error, and weight
When seeking an objectively good tuning of a chosen temperament, what we can do to begin with is find a way to quantify how good a tuning sounds. But it turns out to be easier to quantify how bad it sounds. We accomplish this using a quantity called damage.
We remind you that the purpose of temperament is to give us the consonances we want, without needing as many pitches as we would need with just intonation, and allowing more modulation due to more regular step sizes than just intonation. The price we pay for this is some audible damage to the quality of the intervals due to their cent errors.
The simplest form of damage is how many cents[note 4] off an interval is from its just or pure tuning; in this case, damage is equivalent to the absolute value of the error, where the error means simply the difference in cents between the interval under this tuning of this temperament and the interval in just intonation.[note 5]
For example, in 12-ET, the approximation of the perfect fifth ~3/2 is 700 ¢, which is tuned narrow compared with the just [math]\displaystyle{ \frac{3}{2} }[/math] interval which is 701.955 ¢, so the error here is −1.955 ¢ (negative), while the damage is 1.955 ¢ (positive, as always).
Theoreticians and practitioners frequently choose to weight these absolute errors, in order to capture how some intervals are more important to tune accurately than others. A variety of damage weight approaches are available.
We'll discuss the basics of damage and weighting in the damage section, but we consider the various types of weighting to be advanced concepts and so do not discuss those here (you can read about them in our dedicated article for them).
Target-intervals
In order to quantify damage, we need to know what we're quantifying damage to. These are a set of intervals of our choosing, whose damage we seek to minimize, and we can call them our target-intervals. Typically these are consonant intervals, and in particular they are the consonances that are most likely to be used in the music which the given temperament is being tuned in order to perform; hence our interest in minimizing the damage to them.
If you don't have a specific set of target-intervals in mind already, this article will give some good recommendations for default interval sets to target. To give you a basic idea of what one might look like, for a 5-limit temperament, you might want to use [math]\displaystyle{ \left\{\frac{2}{1}, \frac{3}{1}, \frac{3}{2}, \frac{4}{3}, \frac{5}{2}, \frac{5}{3}, \frac{5}{4}, \frac{6}{5} \right\} }[/math]. But we'll say more about choosing such sets later, in the target-intervals section.
There are even ways to avoid choosing a target-interval set at all, but those are an intermediate-level concept and we won't be getting to those until toward the end of this article.
Held-intervals
Sometimes targeting an interval to minimize its damage is not enough; we insist that absolutely zero damage be dealt to this interval. Most commonly when people want this, it's for the octave. Because we hold this interval to be unchanged, we call it a held-interval of the tuning. You can think of "held" in this context something like "the octave held true", "we held the octave fixed", or "we held onto the octave."
Optimization
With damage being the quantification of how off each of these target-intervals sounds under a given tuning of a given temperament, then optimization means to find the tuning that causes the least overall damage—for some definition of "least overall". Defining exactly what is meant by "least overall", then, is the first issue we will be tackling in detail in this article, coming up next.
Optimization
Just about any reasonable tuning scheme will optimize generator tunings in order to cause a minimal amount of damage to consonant intervals.[note 6] And we can see that tuning schemes may differ by how damage is weighted (if it is weighted at all), and also that they may differ by which intervals' errors are targeted to minimize damage to. But before we unpack those two types of differences, let's first answer this question: given multiple target-intervals whose damages we are all trying to minimize at the same time, how exactly should we define "least overall" damage?
The problem
"Least overall damage"
Consider the following two tunings of the same temperament, and the damages they deal to the same set of target-intervals [math]\displaystyle{ \textbf{i}_1 }[/math], [math]\displaystyle{ \textbf{i}_2 }[/math], and [math]\displaystyle{ \textbf{i}_3 }[/math]:
| [math]\displaystyle{ \textbf{i}_1 }[/math] | [math]\displaystyle{ \textbf{i}_2 }[/math] | [math]\displaystyle{ \textbf{i}_3 }[/math] | |
|---|---|---|---|
| Tuning A | 0 | 0 | 4 |
| Tuning B | 2 | 2 | 1 |
(In case you're wondering about what units these damage values are in, for simplicity's sake, we could assume these absolute errors are not weighted, and therefore quantified as cents. But the units do not really matter for purposes of this discussion, so we don't need to worry about them.)
Which tuning should we choose—Tuning A, or Tuning B?
- Tuning A does an average of [math]\displaystyle{ \dfrac{0 + 0 + 4}{3} = 1.\overline{3} }[/math] damage, while Tuning B does an average of [math]\displaystyle{ \dfrac{2 + 2 + 1}{3} = 1.\overline{6} }[/math] damage, so by that interpretation, [math]\displaystyle{ 1.\overline{3} \lt 1.\overline{6} }[/math] and Tuning A does the least damage.
- However, Tuning B does no more than [math]\displaystyle{ 2 }[/math] damage to any one interval, while Tuning A does all four damage to a single interval, so by that interpretation [math]\displaystyle{ 4 \gt 2 }[/math] and it's Tuning B which does the least damage.
This very simple example illustrates a core problem of tuning: there is more than one reasonable interpretation of "least overall" across a set of multiple target-intervals' damages.
Common interpretations
The previous section has also demonstrated two of the most common interpretations of "least overall" damage that theoreticians use:
- The first interpretation—the one which averaged the individual target-intervals' damages, then chose the least among them—is known as the "minimized average", or miniaverage of the damages.
- The second interpretation—the one which took the greatest from among the individual damages, then chose the least among them—is known as the "minimized maximum", which we shorten to minimax.
There is also a third interpretation of "least overall" damage which is quite common. Under this interpretation, each damage gets squared before averaging, and then that average has its square root taken. Using the above example, then, Tuning A would cause
[math]\displaystyle{ \sqrt{\strut \dfrac{0^2 + 0^2 + 4^2}{3}}= 2.309 }[/math]
damage, while Tuning B would cause
[math]\displaystyle{ \sqrt{\strut \dfrac{2^2 + 2^2 + 1^2}{3}} = 1.732 }[/math]
damage; so Tuning B would be preferred by this statistic too. This interpretation is called the "minimized root mean square", or miniRMS of the damages.
In general, these three interpretations of "least overall" damage will not lead to the same choice of tuning.
A terminological note before we proceed: the term "miniaverage" is not unheard of, though it is certainly less widespread than "minimax", and while "RMS" is well-established, its minimization is not well-known by "miniRMS" (more commonly you will find it referred to by other names, such as "least squares").[note 7] While we appreciate the pedagogical value of deferring to convention, we also appreciate the pedagogical value of consistency, and in this case we have chosen to prioritize consistency.
Rationales for choosing your interpretation
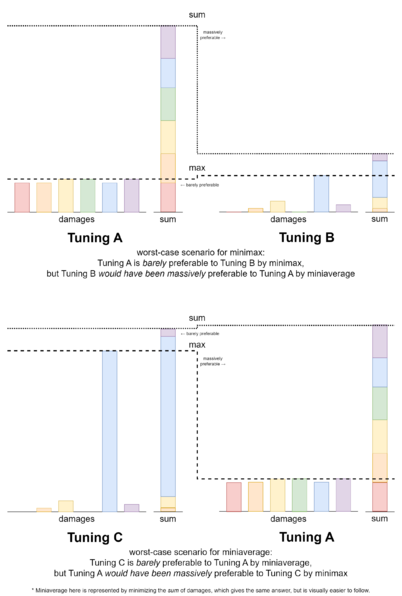
With three different common interpretations of "least overall" damage, you may already be starting to wonder: which interpretation is right for me, from one situation to another, and how would I decide that? To help you answer this for yourself, let's take a moment to talk through how each interpretation influences the end musical results.
We could think of the minimax interpretation as the "weakest link" approach, which is to say that it's based on the thinking that a tuning is only as strong as its weakest interval (the one which has incurred the most damage), so during the optimization procedure we'll be continuously working to improve whichever interval is the weakest at the time. To use another metaphor, we might say that the minimax interpretation is the "one bad apple spoils the bunch" interpretation. As Graham puts it, "A minimax isn't about measuring the total impact, but whether one interval has enough force to break the chord."
In the worst case scenario, a minimax tuning could lead to a relatively large amount of total damage, if it works out to be distributed very evenly across all the target-intervals. Sometimes that's what happens when we focus all of our efforts on minimizing the maximum damage amount.
At the other extreme, the miniaverage is based on the appreciably straightforward thinking that each and every target-interval's damage should be counted. Using this approach, it's sometimes possible to end up with a tuning where many intervals are tuned pure or near pure, while many other intervals are tuned pretty badly, if that's just how the miniaverage calculation works out. So while at a glance this might sound like a sort of communistic tuning where every interval gets its fair share of damage reduction, in fact this is more like a fundamentalist utilitarian society, where resources get distributed however is best for the collective. Finally, miniRMS offers a middle-of-the-road solution, halfway between the effects of minimax and miniaverage. Later on, we'll learn about the mathematical reason why it does this.
If you're unfamiliar with the miniRMS interpretation, it's likely that it seems a bit more arbitrary than the miniaverage and minimax interpretations at first; however, by the end of this article, you will understand that miniRMS actually occupies a special position too. For now, it will suffice to note that miniRMS is related to the formula used for calculating distances in physical space, and so one way to think about it is as a way to compare tunings against each other as if they were points in a multidimensional damage space (where there is one spatial dimension for each target) where "least overall" damage is determined by how close the points are to the origin (the point where no target has any damage, which corresponds to JI).
We note that all but one of the named tuning schemes described on the Xenharmonic wiki is a minimax tuning scheme. But we also think it's important to caution the reader against interpreting this fact as evidence that minimax is clearly the proper interpretation of "least overall" damage. This predominance of named tuning schemes that are minimax tuning schemes may be due to a historical proliferation of named tuning schemes which cleverly get around the need to specify a target-interval set (these were mentioned earlier, and we're still not ready to discuss them in detail), and it turns out that being a minimax tuning scheme is one of the two necessary conditions to achieve that effect. And as alluded to earlier, while these schemes with no specific target have value for consistent, reasonable, and easy-to-compute documentation, they do not necessarily result in the most practical or nicest-sounding tunings that you would want to actually use for your music.
Tuning space
Our introductory example was simple to the point of being artificial. It presented a choice between just two tunings, Tuning A and Tuning B, and this choice was served to us on a silver platter. Once we had decided upon our preferred interpretation of "least overall" damage, the choice of tuning was straightforward: all that remained to do at that point was to compute the damage for both of the tunings, and choose whichever one of the two caused less damage.
In actuality, choosing a tuning is rarely this simple, even after deciding upon the interpretation of "least overall" damage.
Typically, we find ourselves confronting way more than two tunings to choose between. Instead, we face an infinite continuum of possible tunings to check! We can call this range of possibilities our tuning space. If a temperament has one generator, i.e. it is rank-1, then this tuning space is one-dimensional—a line—somewhere along which we'll find the tuning causing the minimum damage, and at this point narrowing down the right place to look isn't too tricky. But if a temperament has two generators, though, the tuning space we need to search is therefore two-dimensional—an entire plane, infinity squared: for each of the infinitude of possibilities for one generator, we find an entire other infinitude of possibilities for the other generator. And for rank-3 temperaments the space becomes 3D—a volume, so now we're working with infinity cubed. And so on. We can see how the challenge could quickly get out of hand, if we didn't have the right tools ready.
Tuning damage space
Each one of these three interpretations of "least overall" damage involves minimizing a different damage statistic.
- The miniaverage interpretation seeks out the minimum value of the average of the damages, within the limitations of the temperament.
- The minimax interpretation seeks out the minimum value of the max of the damages, within the limitations of the temperament.
- The miniRMS interpretation seeks out the minimum value of the RMS of the damages, within the limitations of the temperament.
So, for example, when we seek a miniaverage tuning of a temperament, we essentially visit every point—every tuning—in our tuning space, evaluating the average damage at that point (computing the damage to each of the target-intervals, for that tuning, then computing the average of those damages), and then we choose whichever of those tunings gave the minimum such average. The same idea goes for the minimax with the max damage, and the miniRMS with the RMS damage.
We can imagine taking our tuning space and adding one extra dimension on which to graph the damage each tuning causes, whether that be to each target-interval individually, or a statistic across all target-intervals's damages like their average, max, or RMS, or several of these at once. This type of space we could call "tuning damage space".
So the tuning damage space for a rank-1 temperament is 2D: the generator tunings along the [math]\displaystyle{ x }[/math]-axis, say, and the damage along the [math]\displaystyle{ y }[/math]-axis.
And the tuning damage space for a rank-2 temperament is 3D: the generator tunings along the [math]\displaystyle{ x }[/math]- and [math]\displaystyle{ y }[/math]- axes, and the damage along the [math]\displaystyle{ z }[/math]-axis.
By the way, the damage space we mentioned earlier when explaining the RMS is a different type of space than tuning damage space. For damage space, every dimension is a damage dimension, and no dimensions are tuning dimensions; there, tunings are merely labels on points in space. So tuning damage space is much more closely related to tuning space than it is to damage space, because it's basically tuning space but with one single extra dimension added for the tunings' damages.
2D tuning damage graphs
It is instructive to visualize the relationship between individual target-interval damages and these damage statistics that we're seeking to minimize. (Don't worry about the angle bracket notation we're using for the means here; we'll explain it a little later.)
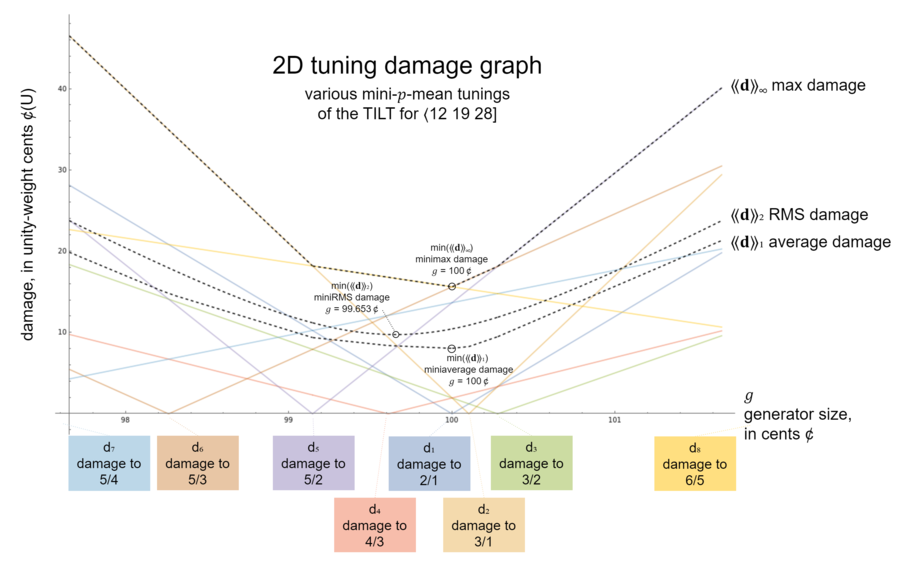
This graph visualizes a simple introductory example of a rank-1 (equal) temperament, that is, a temperament which has only a single generator. So as we discussed previously, because we have only one generator that we need to tune, the entire problem—the tuning damage space—can be visualized on a 2D graph. The horizontal axis of this graph corresponds with a continuum of size for the generator: narrow on the left, wide on the right. The vertical axis of this graph shows how much damage is dealt to each interval given that generator tuning. The overall impression of the graph is that there's a generator tuning somewhere in the middle here which is best, and generator tunings off the left and right edges of the graph are of no interest to us, because the further you go in either direction the more damage gets piled on.
Firstly, note that each target-interval's damage makes a V-shaped graph. If you're previously familiar with the shape of the absolute value graph, this should come as no surprise. For each target-interval, we can find a generator tuning that divides into the target-interval's size exactly, with no remainder, and thus the target-interval is tuned pure there (the error is zero, and therefore it incurs zero damage). This is the tip of the V-shape, where it touches the horizontal axis. To the right of this point, the generator is slightly too wide, and so the interval is tuned wide; the error here is positive and thus it incurs some damage. And to the left of this point, the generator is slightly too narrow, and so the interval is tuned narrow; the error here is negative, and due to damage being the absolute value of the error, the damage is also positive.
For this example we have chosen to target eight intervals' damages to optimize for. These are [math]\displaystyle{ \frac{2}{1} }[/math], [math]\displaystyle{ \frac{3}{1} }[/math], [math]\displaystyle{ \frac{3}{2} }[/math], [math]\displaystyle{ \frac{4}{3} }[/math], [math]\displaystyle{ \frac{5}{2} }[/math], [math]\displaystyle{ \frac{5}{3} }[/math], [math]\displaystyle{ \frac{5}{4} }[/math], and [math]\displaystyle{ \frac{6}{5} }[/math]. (We call this set the "6-TILT" which is short for "truncated 6-integer-limit triangle".[note 8] TILTs, our preferred kind of target-interval set will be explained later.)
So each of these eight intervals makes its own V-shaped graph. The V-shapes do not line up exactly, because the intervals are not all tuned pure at the same generator tuning. So when we put them all together, we get a unique landscape of tuning damage, something like a valley among mountains.
Note that part of what makes this landscape unique is that the steepness differs from one V-shape to the next. This has to do with how many generators it takes to approximate each target-interval. If one target-interval is approximated by 2 steps of the generator and another target-interval is approximated by 6 steps of the generator, then the latter target-interval will be affected by damage to this generator 3 times as much as the former target-interval, and so its damage graph will be 3 times as steep. (If we were using a simplicity- or complexity- weight damage, the complexity of the interval would affect the slope, too.)
Also note that the minimax damage, miniaverage damage, and miniRMS damage are each represented by a single point on this graph, not a line. Each one is situated at the point of the minimum value along the graph of a different damage statistic—the max damage, average damage, and RMS damage, respectively.
We can see that the max damage sits just on top of this landscape, as if it were a layer of snow on the ground. It is a graph consisting of straight line segments and sharp corners, like the underlying V's themselves. The average damage also consists of straight line segments and sharp corners, but travels through the mountains. We may notice that the max damage line has a sharp corner wherever target-interval damage graphs cross up top above all others, while the average damage line has a sharp corner wherever target-interval damage graphs bounce off the bottom.
The RMS damage is special because it consists of a single long smooth curve, with no straight segments or corners to it at all. This should be unsurprising, though, if one is familiar with the hyperbolic shape of the graph [math]\displaystyle{ y = x^2 }[/math], and recognizes RMS as the sum of eight different offset copies of this graph (divided by a constant, and square rooted, but those parts don't matter so much). We also see that the RMS graph is found vertically in between the average and max graphs.
3D tuning damage graphs
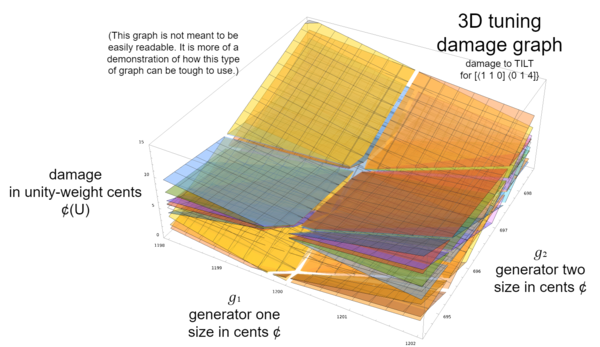
Before we move on, we should also at least glance at what tuning graphs look like for rank-2 temperaments. As we mentioned a bit earlier, when you have one dimension for each of two generators, then you need a third dimension to graph damage into. So a rank-2 temperament's tuning damage graph is 3D. Here's an example:
Even with the relatively small count of eight target-intervals, this graph appears as a tangled mess of bent-up-looking intersecting planes and curves. In order to see better what's going on, let's break it down into all of its individual graphs (and including some key average damage graphs as well):
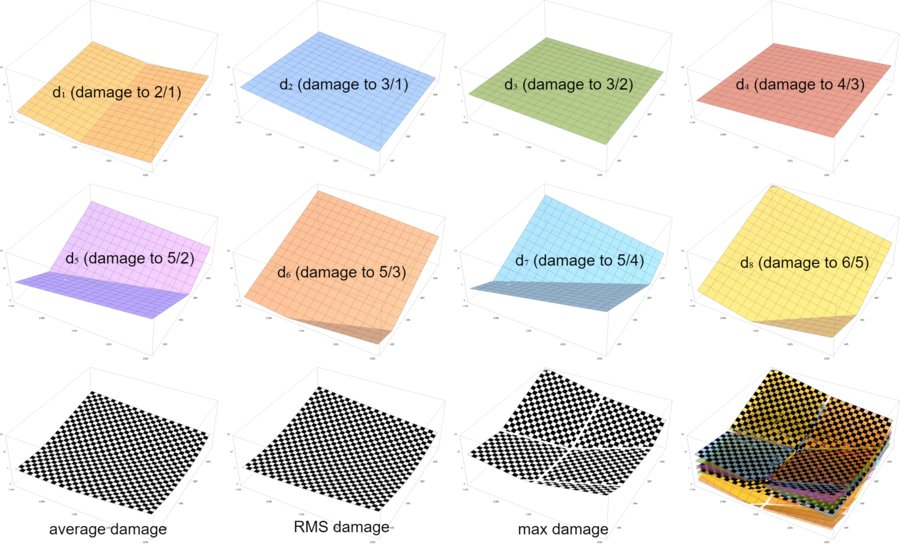
Now we can actually see the shape of each of the target-intervals' graphs. Notice that it's still sort of a V, but a three-dimensional one. In general we could say that the shape of a target-interval's tuning damage graph is a "hyper-V". In 2D tuning damage space, that means just a V-shape, but in 3D tuning damage space like this, they look like V's that have been extruded infinitely in both directions along the axis which you would look at them straight on. In other words, it's just two planes coming down and toward each other to meet at a line angled across the ([math]\displaystyle{ x }[/math], [math]\displaystyle{ y }[/math])-floor (that line being the line along which the proportions of the two generators are constant, and tune the given target-interval purely). You could think of a hyper-V as a hyperplane with a single infinitely long crease in it, wherever it bounces off the pure-tuning floor, due to that taking of the absolute value involved in the damage calculation. In 4D and beyond it's difficult to visualize directly, but you can try to extrapolate this idea.
But what about the max, average, and RMS graphs? In 2D, they looked like V's too, just with rounded-off or crinkled-up tips. Do they look like hyper-V's in 3D too, just with rounded-off or crinkled-up tips? Well, no, actually! They do keep their rounded-off or crinkled-up tip aspect, but when they take to higher dimensions, they do so in the form not of a hyper-V, but in the form of a hyper-cone.
Topographic tuning damage graphs
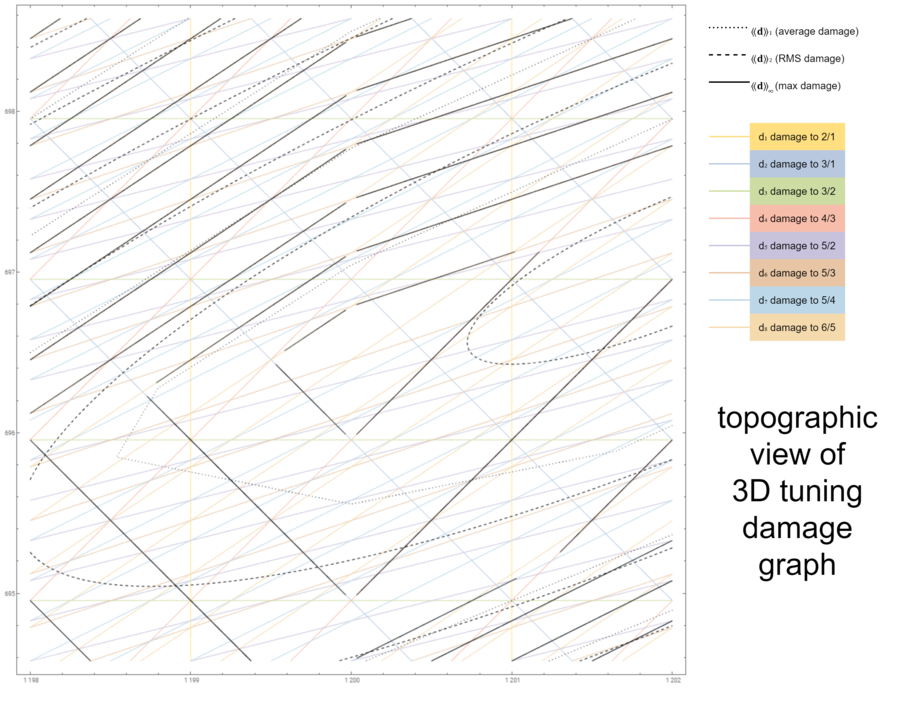
If 3D graphs aren't your thing, there's another helpful way to visualize tuning damage for rank-2 temperaments: with a topographic graph. These are basically top-down views of the same information, with lines tracing along places where the damage is the same. If you've ever looked at a geographic map which showed elevation information with contours, then you'll immediately understand how these graphs work.
Here's an example, showing the same information as the chart in the previous section. Note that with this view, it's easier to see that the minima for the average and RMS damage may not even be in this sector! Whereas we could barely tell that when we were looking at the perspective view; we could only really discern the max damage minimum (the minimax) since it's on top, so much easier to see.
Power means
Each of these damage statistics we've been looking at—the average, the max, and the RMS—can be understood as a power mean, or [math]\displaystyle{ p }[/math]-mean. Let's take a look at these in more detail now.
Steps
All of these power means can be defined with a single unifying formula, which situates them along a continuum of possibilities, according to that power [math]\displaystyle{ p }[/math].
Here are the steps of a [math]\displaystyle{ p }[/math]-mean:
- We begin by raising each item to the [math]\displaystyle{ p }[/math]th power.
- We then sum up the items.
- Next, we divide the sum by [math]\displaystyle{ k }[/math], the count of items.
- We finish up the [math]\displaystyle{ p }[/math]-mean by taking the matching root at the end, that is, the root matching the power that each item was individually raised to in the first step; so that's the [math]\displaystyle{ p }[/math]th root. If, for example, the items were squared at the start—that is, we took their 2nd power—then at the end we take the square root—the 2nd root.
Formula
So here is the overall formula:
[math]\displaystyle{
\llangle\textbf{d}\rrangle_p = \sqrt[p]{\strut \dfrac{\sum\limits_{n=1}^k d_n^p}{k}}
}[/math]
We can expand this out like so:
[math]\displaystyle{
\llangle\textbf{d}\rrangle_p = \sqrt[p]{\strut \dfrac{d_1^p + d_2^p + ... + d_k^p}{k}}
}[/math]
If the formula looks intimidating, the straightforward translation of it is that for some target-interval damage list [math]\displaystyle{ \textbf{d} }[/math], which has a total of [math]\displaystyle{ k }[/math] items (one for each target-interval), raise each item to the [math]\displaystyle{ p }[/math]th power and then sum them up. Then divide by [math]\displaystyle{ k }[/math], and take the [math]\displaystyle{ p }[/math]th root. What we have here is nothing but the mathematical form of the steps given in the previous section.
The double angle bracket notation for the [math]\displaystyle{ p }[/math]-mean shown above, [math]\displaystyle{ \llangle\textbf{d}\rrangle_p }[/math], is not a conventional notation. This is a notation we (Dave and Douglas) came up with, as a variation on the double vertical-bar brackets used to represent the related mathematical operation called the power norm (which you can learn more about in our later article on all-interval tunings), and was inspired by the use of single angle brackets for the average or expected value in physics. You may see the notation [math]\displaystyle{ M_p(\textbf{d}) }[/math] used elsewhere, where the "M" stands for "mean". We do not recommend or use this notation as it looks too much like a mapping matrix [math]\displaystyle{ M }[/math].
So how exactly do the three power means we've looked at so far—average, RMS, and max—fit into this formula? What power makes the formula work for each one of them?
Average
Well, let's look at the average first. You may be previously familiar with the concept of an average from primary education, sometimes also called the "mean" and taught along with the concepts of the median and the mode. The power mean is a generalization of this standard concept of a mean (and for that reason it is also sometimes referred to as the "generalized mean"). It is a generalization in the sense that the standard mean is equivalent to one particular power of [math]\displaystyle{ p }[/math]: 1. The power-of-[math]\displaystyle{ 1 }[/math] and the root-of-[math]\displaystyle{ 1 }[/math] steps have no effect, so really all the [math]\displaystyle{ 1 }[/math]-mean does is sum the items and divide by their count, which is probably exactly how you were taught the standard mean back in school. So the power mean is a powerful (haha) concept that allows us to generalize this idea to other combinations of powers and roots besides boring old [math]\displaystyle{ 1 }[/math].
So to be clear, the power [math]\displaystyle{ p }[/math] for the average is [math]\displaystyle{ 1 }[/math]; the average is AKA the [math]\displaystyle{ 1 }[/math]-mean or "mean" for short (though we avoid referring to it as such in our articles, to avoid confusion with the generalized mean).
RMS
As for the RMS, that's just the [math]\displaystyle{ 2 }[/math]-mean.
Max
But what about the max? Can you guess what value of [math]\displaystyle{ p }[/math], that is, which power would cause a power mean to somehow pluck the maximum value from a list? If you haven't come across this neck of the mathematical woods before, this may come across as a bit of a trick question. That's because the answer is: infinity! The max function is equivalent to the [math]\displaystyle{ ∞ }[/math]-mean: the infinitieth root of the sum of infinitieth powers.
It turns out that when we take the [math]\displaystyle{ ∞ }[/math]th power of each damage, add them up, divide by the count, and then take the [math]\displaystyle{ ∞ }[/math]th root, the mathemagical result is that we get whichever damage had been the maximum. One way to think about this effect is that when all the damages are propelled into infinity, whichever one had been the biggest to begin with dominates all the others, so that when we (divide by the count and then) take the infinitieth root to get back to the size we started with, it's all that remains.[note 9] It's fascinating stuff. So while the average human would probably not naturally think of the problem "find the maximum" in this way, this is apparently just one more mathematically feasible way to think about it. And we'll come to see later—when learning about non-unique tunings—why this interpretation of the max is important to tuning.[note 10]
The average reader[note 11] of this article will probably feel surprised to learn that the max is a type of mean, since typically these statistics are taught as mutually exclusive fundamentals with very different goals. But so it is.
Examples
For examples of mean damages in existing RTT literature, we can point to Paul's "max damage" in his tables in A Middle Path, or Graham's "adjusted error" and "TE error" in his temperament finder's results.
Minimized power means
The category of procedures that return the minimization of a given [math]\displaystyle{ p }[/math]-mean may be called "minimized power means", or "mini-[math]\displaystyle{ p }[/math]-means" for short. The minimax, miniRMS, and miniaverage are all examples of this: the mini-[math]\displaystyle{ 1 }[/math]-mean, mini-[math]\displaystyle{ 2 }[/math]-mean, and mini-[math]\displaystyle{ ∞ }[/math]-mean, respectively.
We can think of the term "minimax" as a cosmetic simplification of "mini-[math]\displaystyle{ ∞ }[/math]-mean", where since "max" is interchangeable with "[math]\displaystyle{ ∞ }[/math]-mean", we can swap "max" in for that, and collapse the remaining hyphen. Similarly, we can swap "RMS" in for "[math]\displaystyle{ 2 }[/math]-mean", and collapse the remaining hyphen, finding "miniRMS", and we can swap "average" in for "[math]\displaystyle{ 1 }[/math]-mean", and collapse the remaining hyphen, finding "miniaverage".
Function vs procedure
A [math]\displaystyle{ p }[/math]-mean and a mini-[math]\displaystyle{ p }[/math]-mean are very different from each other.
- A [math]\displaystyle{ p }[/math]-mean is a simple mathematical function. Its input is a list of damages, and its output is a single mean damage. It can be calculated in a tiny fraction of a second.
- A mini-[math]\displaystyle{ p }[/math]-mean, on the other hand, is a much more complicated kind of thing called an optimization procedure. Configured with the information about the current temperament and tuning scheme, and using various fancy algorithms developed over the centuries by specialized mathematicians, it intelligently tests anywhere from a few candidate tunings to hundreds of thousands of candidate tunings, finding the overall damage for each of them, where “overall” is defined by the given [math]\displaystyle{ p }[/math]-mean, searching for the candidate tuning which does the least overall damage. A mini-[math]\displaystyle{ p }[/math]-mean may take many seconds or sometimes even minutes to compute.
So when we refer to a "mini-[math]\displaystyle{ p }[/math]-mean" on its own, we're referring to this sort of optimization procedure. And when we say the "mini-[math]\displaystyle{ p }[/math]-mean tuning", we're referring to its output—a list of generator tunings in cents per generator (a generator tuning map). Finally, when we say the "mini-[math]\displaystyle{ p }[/math]-mean damage", we're referring to the minimized mean damage found at that optimum tuning.
Optimization power
Because optimum tunings are found as power minima of damage, we can refer to the chosen [math]\displaystyle{ p }[/math] for a tuning scheme as its optimization power. So the optimization power [math]\displaystyle{ p }[/math] of a minimax tuning scheme is [math]\displaystyle{ ∞ }[/math], that of a miniaverage tuning scheme is [math]\displaystyle{ 1 }[/math], and that of a miniRMS tuning scheme is [math]\displaystyle{ 2 }[/math].
Other powers
So far we've only given special attention to powers [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], and [math]\displaystyle{ ∞ }[/math]. Other powers of [math]\displaystyle{ p }[/math]-means are certainly possible, but much less common. Nothing is stopping you from using [math]\displaystyle{ p = 3 }[/math] or [math]\displaystyle{ p = 1.5 }[/math] if you find that one of these powers regularly returns the tuning that is most pleasant to your ears.
Computing tunings by optimization power
The short and practical answer to the question: "How should I compute a particular optimization of damages?" is: "Just give it to a computer." Again, the RTT Library in Wolfram Language is ready to go; its README explains how to request the exact optimization power you want to use (along with your preferred intervals whose damages to target, and how to weight damage if at all, though we haven't discussed these choices in detail yet). Even for a specialized RTT tuning library, the general solution remains essentially to hand a mathematical expression off to Wolfram's specialized mathematical functionality and ask it politely to give you back the values that minimize this expression's value, using whichever algorithms it automatically determines are best to solve that sort of problem (based on the centuries of mathematical innovations that have been baked into this programming language designed specifically for math problems).
That said, there are special computational tricks for the three special optimization powers we've looked at so far—[math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], and [math]\displaystyle{ ∞ }[/math]—and familiarizing yourself with them may deepen your understanding of the results they return. To be clear, powers like [math]\displaystyle{ 1.5 }[/math] and [math]\displaystyle{ 3 }[/math] have no special computation tricks; those you really do just have to hand off to a computer algorithm to figure out for you. The trick for [math]\displaystyle{ p=2 }[/math] will be given some treatment later on in this series, in our article about tuning computation; a deeper dive on tricks for all three powers may be found in the article Generator embedding optimization.
Non-unique tunings
Before concluding the section on optimization powers, we should make sure to warn you about a situation that comes up only with optimization powers [math]\displaystyle{ 1 }[/math] and [math]\displaystyle{ ∞ }[/math]. Mercifully, you don't have to worry about this for any other power [math]\displaystyle{ 1 \lt p \lt ∞ }[/math]. The situation is this: you've asked for a miniaverage ([math]\displaystyle{ p = 1 }[/math]) or minimax ([math]\displaystyle{ p = ∞ }[/math]) tuning, but rather than being taken straight to a single correct answer, you find that there at first glance seems to be more than one correct answer. In other words, more than one tuning can be found that gives the same miniaverageed or minimaxed amount of damage across your target-intervals. In fact, there is an entire continuous range of tunings which satisfy the condition of miniaveraging or minimaxing damage.
Not to worry, though—there is always a good way to define a single tuning from within that range as the true optimum tuning. We shouldn't say that there is more than one minimax tuning or more than one miniaverage tuning in these cases, only that there's nonunique minimax damage or nonunique miniaverage damage. You'll see why soon enough.
Example
For example, suppose we ask for the tuning that gives the miniaverage of damage (without weighting, i.e. absolute value of error) to the truncated integer limit triangle under magic temperament. Tuning our generators to Tuning A, 1200.000 ¢ and 380.391 ¢, would cause an average of 2.961 ¢(U) damage across our eight target-intervals, like this:
[math]\displaystyle{ \begin{array} {lccccccccccccccc} & & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\ \textbf{d}_ᴀ & = & [ & 0.000 & 0.000 & 0.000 & 0.000 & 5.923 & 5.923 & 5.923 & 5.923 & ] \\ \end{array} }[/math]
[math]\displaystyle{ \begin{align} \llangle\textbf{d}_ᴀ\rrangle_1 &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{0.000^1 + 0.000^1 + 0.000^1 + 0.000^1 + 5.923^1 + 5.923^1 + 5.923^1 + 5.923}{8}} \\ &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{0.000 + 0.000 + 0.000 + 0.000 + 5.923 + 5.923 + 5.923 + 5.923^1}{8}} \\ &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{23.692}{8}} \\ &= \sqrt[1]{\strut 2.961} \\ &= 2.961 \\ \end{align} }[/math]
But we have another option that ties this 2.961 ¢(U) value! If we tune our generators to Tuning B, 1202.961 ¢ and 380.391 ¢ (same major third generator, but an impure octave this time), we cause that same total damage amount, just in a completely different way:
[math]\displaystyle{ \begin{array} {lccccccccccccccc} & & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\ \textbf{d}_ʙ & = & [ & 2.961 & 0.000 & 2.961 & 5.923 & 2.961 & 0.000 & 5.923 & 2.961 & ] \\ \end{array} }[/math]
[math]\displaystyle{ \begin{align} \llangle\textbf{d}_ʙ\rrangle_1 &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{2.961^1 + 0.000^1 + 2.961^1 + 5.923^1 + 2.961^1 + 0.000^1 + 5.923^1 + 2.961^1}{8}} \\ &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{2.961 + 0.000 + 2.961 + 5.923 + 2.961 + 0.000 + 5.923 + 2.961}{8}} \\ &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{23.692}{8}} \\ &= \sqrt[1]{\strut 2.961} \\ &= 2.961 \\ \end{align} }[/math]
And just to prove the point about this damage being tied along a range of possibilities, let's take a tuning halfway in between these two, Tuning C, with an octave of 1201.481 ¢:
[math]\displaystyle{ \begin{array} {lccccccccccccccc} & & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\ \textbf{d}_ᴄ & = & [ & 1.481 & 0.000 & 1.481 & 2.961 & 4.442 & 2.961 & 5.923 & 4.442 & ] \\ \end{array} }[/math]
[math]\displaystyle{ \begin{align} \llangle\textbf{d}_ᴄ\rrangle_1 &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{1.481^1 + 0.000^1 + 1.481^1 + 2.961^1 + 4.442^1 + 2.961^1 + 5.923^1 + 4.442^1}{8}} \\ &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{1.481 + 0.000 + 1.481 + 2.961 + 4.442 + 2.961 + 5.923 + 4.442}{8}} \\ &= \sqrt[\Large{1}]{\rule[15pt]{0pt}{0pt} \dfrac{23.692}{8}} \\ &= \sqrt[1]{\strut 2.961} \\ &= 2.961 \\ \end{align} }[/math]
(Don't worry too much about rounding errors throughout these examples.)
We can visualize this range of tied miniaverage damage tunings on a tuning damage graph:
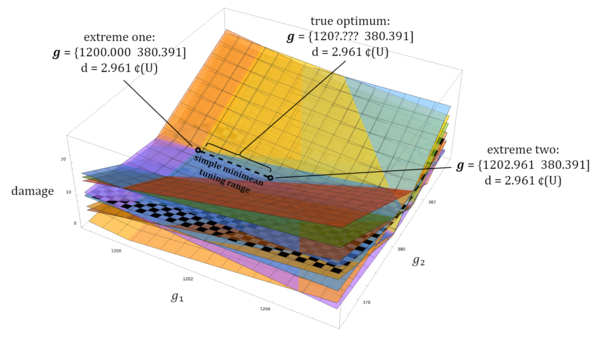
Damages are plotted on the [math]\displaystyle{ z }[/math]-axis, i.e. coming up from the floor, so the range where tunings are tied for the same miniaverage damage is the straight line segment that is exactly parallel with the floor.
True optimum
So... what to do now? How should we decide which tuning from this range to use? Is there a best one, or is there even a reasonable objective answer to that question?
Fortunately, there is a reasonable objective best tuning here, or as we might call it, a true optimum. To understand how to choose it, though, we first need to understand a bit more about why we wind up with ranges of tunings that are all tied for the same damage.
Power continuum
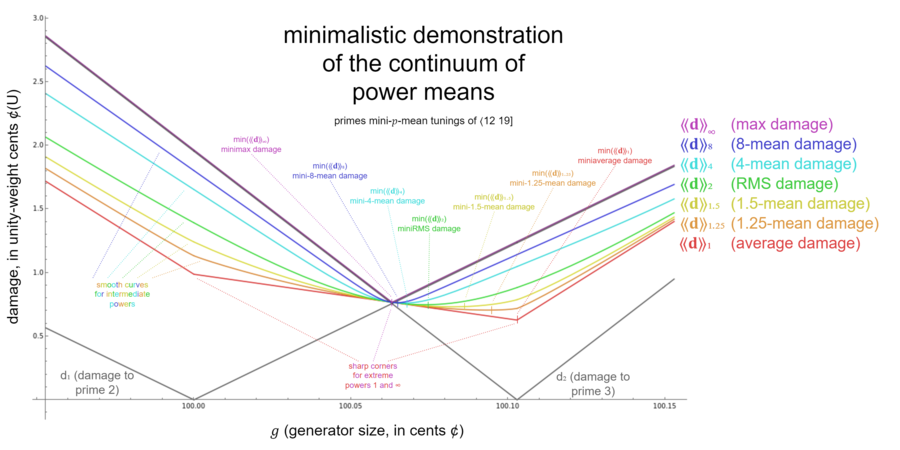
To illustrate the case of the miniaverage, we can use a toy example. Suppose we have the rank-1 temperament in the 3-limit ⟨12 19], our target-intervals are just the two primes [math]\displaystyle{ \frac{2}{1} }[/math] and [math]\displaystyle{ \frac{3}{1} }[/math], and we do not weight absolute error to obtain damage. Our tuning damage graph looks like this:
We have also plotted several power means here: [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 1\frac{1}{4} }[/math], [math]\displaystyle{ 1\frac{1}{2} }[/math], [math]\displaystyle{ 2 }[/math], [math]\displaystyle{ 4 }[/math], [math]\displaystyle{ 8 }[/math], and [math]\displaystyle{ ∞ }[/math]. Here we see for the first time a vivid visualization of what we were referring to earlier when we spoke of a continuum of powers. And we can also see why it was important to understand how the maximum of a list of values can be interpreted as the [math]\displaystyle{ ∞ }[/math]-mean, i.e. the [math]\displaystyle{ ∞ }[/math]th root of summed values raised to the [math]\displaystyle{ ∞ }[/math]th power. We can see that as the power increases from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ 2 }[/math], the blocky shape smooths out into a curve, and then as the power increases from [math]\displaystyle{ 2 }[/math] to [math]\displaystyle{ ∞ }[/math] it begins reverting back from a smooth shape into a blocky shape again, but this time hugged right onto the individual target-intervals' graphs.
The first key thing to notice here is that every mean except the [math]\displaystyle{ 1 }[/math]-mean and [math]\displaystyle{ ∞ }[/math]-mean have a curved graph; it is only these two extremes of [math]\displaystyle{ 1 }[/math] and [math]\displaystyle{ ∞ }[/math] which sharpen up into corners. Previously we had said that the [math]\displaystyle{ 2 }[/math]-mean was the special one for being curved, because at that time we were only considering powers [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], and [math]\displaystyle{ ∞ }[/math]; when all possible powers are considered, though, it is actually [math]\displaystyle{ 1 }[/math] and [math]\displaystyle{ ∞ }[/math] that are the exceptions with respect to this characteristic of means.
The second key thing to notice is that due to the [math]\displaystyle{ 1 }[/math]-mean's straight-lined characteristic, it is capable of achieving the situation where one of its straight line segments is exactly parallel with the bottom of the graph. We can see that all along this segment, the damage to prime 2 is decreasing while the damage to prime 3 is increasing, or vice versa, depending on which way you're going along it; in either case, you end up with a perfect tradeoff so that the total damage remains the same in that sector. This is the bare minimum illustration of a tied miniaverage damage tuning range.
A tied minimax range is demonstrated in the pajara graph below.
How to choose the true optimum
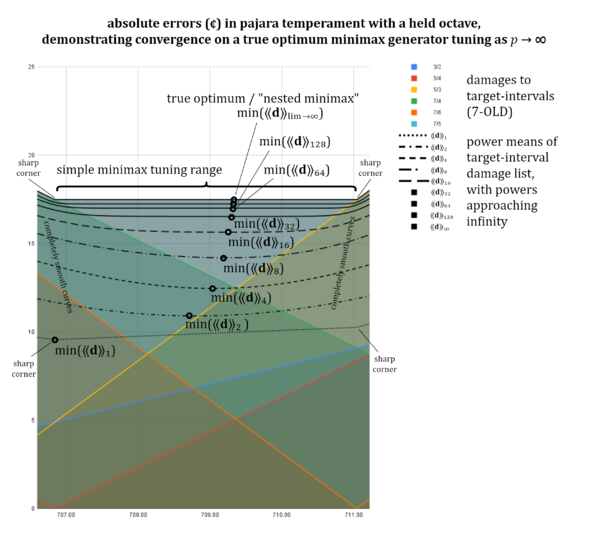
We're now ready to explain how miniaverage and minimax tuning schemes can find a true optimum tuning, even if their miniaverage or minimax result is not unique. The key thing to realize is that any of these mean graphs that make a smooth curve—whether it's the one with power [math]\displaystyle{ 2 }[/math], [math]\displaystyle{ 4 }[/math], [math]\displaystyle{ 8 }[/math], or [math]\displaystyle{ 1\frac{1}{2} }[/math] or [math]\displaystyle{ 1\frac{1}{4} }[/math]—they will have a definite singular minimum wherever the bottom of their curve is. We can choose a smaller and smaller power—[math]\displaystyle{ 1\frac{1}{8} }[/math], [math]\displaystyle{ 1\frac{1}{16} }[/math], [math]\displaystyle{ 1\frac{1}{32} }[/math], [math]\displaystyle{ 1\frac{1}{64} }[/math] on and on—and as long as we don't actually hit [math]\displaystyle{ 1 }[/math], the graph will still have a single minimum. It will get closer and closer to the shape of the 1-mean graph, but if you zoom in very closely, you will find that it still doesn't quite have sharp corners yet, and critically, that it doesn't quite have a flat bottom yet. (The same idea goes for larger and larger powers approaching [math]\displaystyle{ ∞ }[/math], and minimax.)
As the power decreases or increases like this, the value of that single minimum changes. It changes a lot, relatively speaking, in the beginning. That is, the change from [math]\displaystyle{ p=2 }[/math] to [math]\displaystyle{ p=4 }[/math] is significant, but then the change from [math]\displaystyle{ p=4 }[/math] to [math]\displaystyle{ p=8 }[/math] is less so. And the change from [math]\displaystyle{ 8 }[/math] to [math]\displaystyle{ 16 }[/math] is even less so. By the time you're changing from [math]\displaystyle{ 64 }[/math] to [math]\displaystyle{ 128 }[/math], the value is barely changing at all. At a certain point, anyway, the amount of change is beyond musical relevance for any human listener.
Mathematically we describe this situation as a limit, meaning that we have some function whose output value cannot be directly evaluated for some input value, however, we can check the output values as we get closer and closer to the true input value we care about—infinitely/infinitesimally close, in fact—and that will give us a "good enough" type of answer. So in this case, we'd like to know the minimum value of the mean graph when [math]\displaystyle{ p=∞ }[/math], but that's undefined, so instead we check it for something like [math]\displaystyle{ p=128 }[/math], some very large value. What exact value we use will depend on the particulars of the software doing the job, its strengths and limitations. But the general principle is to methodically check closer and closer powers to the limit power, and stop whenever the output value is no longer changing appreciably, or when you run into the limitations of your software's numeric precision.
So we could say that the complete flattening of the miniaverage and minimax graphs is generally beneficial, in that the methods for finding exact solutions for optimum tunings rely on it, but on occasion it does cause the loss of an important bit of information—the true optimum—which can be retrieved by using a power very close to either [math]\displaystyle{ 1 }[/math] or [math]\displaystyle{ ∞ }[/math].
(Note: the example given in the diagram here is a bit silly. The easiest way to break the tie in this case would be to remove the offending target-interval from the set, since with constant damage, it will not aid in preferring one tuning to another. However, more natural examples of tied tunings—that cannot be resolved so easily—require 3D tuning damage space, and we sought to demonstrate the basic principle of true optimum tunings as simply as possible, so we stuck with 2D here.)
A final note on the true optimum tuning for a minimax or miniaverage tuning scheme
The true optimum tuning for a minimax tuning scheme, in addition to thinking of it as the limit of the [math]\displaystyle{ p }[/math]-mean as [math]\displaystyle{ p }[/math] approaches infinity, can also be thought of as the tuning which not only achieves the minimax damage, but furthermore, if the target-intervals tied for being dealt this maximum damage were removed from the equation, the damage to all the remaining intervals would still be minimaxed within this outer minimax. And if a tie were found at this tier as well, the procedure would continue to further nested minimaxes.
More information on this situation can be found where the computation approach is explained for tie-breaking with this type of tuning scheme, here: Generator embedding optimization#Coinciding-damage method.
Damage
In the previous section, we looked at how the choice of optimization power—in other words, how we define the "least overall" part of "least overall damage"—affects tuning. In this section, then, we will look at how the way we define "damage" affects tuning.
Definitions of damage differ by how the absolute error is weighted. As mentioned earlier, the simplest definition of damage does not use weights, in which case it is equivalent to the absolute value of the error.
Complexity
Back in the initial definitions section, we also mentioned how theorists have proposed a wide variety of ways to weight damage, when it is weighted at all. These ways may vary quite a bit between each other, but there is one thing that every damage weight described on the Xenharmonic wiki (thus far) has in common: it is defined in terms of a complexity function.[note 12]
A complexity function, plainly put, is used to objectively rank musical interval ratios according to how complex they are. A larger complexity value means a ratio is more complex. For example, [math]\displaystyle{ \frac{32}{21} }[/math] is clearly a more complex ratio than [math]\displaystyle{ \frac{3}{2} }[/math], so if [math]\displaystyle{ \frac{32}{21} }[/math]'s complexity was 10 then maybe [math]\displaystyle{ \frac{3}{2} }[/math]'s complexity would be something like 5.
For a more interesting example, [math]\displaystyle{ \frac{10}{9} }[/math] may seem like it should be a more complex ratio than [math]\displaystyle{ \frac{9}{8} }[/math], judging by its slightly bigger numbers and higher prime limit. And indeed it is ranked that way by the complexity function that we consider to be a good default, and which we'll be focusing on in this article. But some complexity functions do not agree with this, ranking [math]\displaystyle{ \frac{9}{8} }[/math] as more complex than [math]\displaystyle{ \frac{10}{9} }[/math], and yet theoreticians still commonly use these complexities.[note 13]
Product complexity and log-product complexity
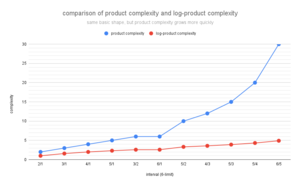
Probably the most obvious complexity function for JI interval ratios is product complexity, which is the product of the numerator and denominator. So [math]\displaystyle{ \frac{3}{2} }[/math]'s product complexity is [math]\displaystyle{ 3 × 2 = 6 }[/math], and [math]\displaystyle{ \frac{32}{21} }[/math]'s product complexity is [math]\displaystyle{ 32 × 21 = 672 }[/math]. For reasons that don't need to be delved into until a later article, we usually take the base 2 logarithm of this value, though, and call it the log-product complexity.
As we saw with power means earlier, taking the logarithm doesn't change how complexities compare relative to each other. If an interval was more complex than another before taking the log, it will still be more complex than it after taking the log. All this taking of the logarithm does is reduce the differences between values as they get larger, causing the larger values to bunch up more closely together.
Let's take a look at how this affects the two product complexity values we've already looked at. So [math]\displaystyle{ \frac{3}{2} }[/math]'s log-product complexity is [math]\displaystyle{ \log_2{6} \approx 2.585 }[/math] and [math]\displaystyle{ \frac{32}{21} }[/math]'s log-product complexity is [math]\displaystyle{ \log_2{672} \approx 9.392 }[/math]. We can see that not only are both the values smaller than they were before, the latter value is much smaller than it used to be.
But enough about logarithms in complexity formulas for now. We'll wait until later to look into other such complexity formulas (in the alternative complexities article).
Weight slope
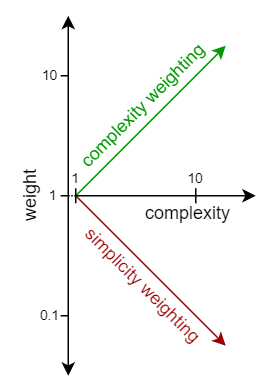
What's more important to cover right away is that—regardless of the actual choice of complexity formula—a major disagreement among tuning theorists is whether, when choosing to weight absolute errors by complexity, to weight them so that more attention is given to the more complex intervals, or so that more attention is given to the less complex intervals.
We call this trait of tuning schemes damage weight slope, because on a graph with interval complexity increasing from left to right along the [math]\displaystyle{ x }[/math]-axis and the weight (importance) of the error in each interval increasing from bottom to top along the [math]\displaystyle{ y }[/math]-axis, this trait determines how the graph slopes, either upwards or downwards as it goes to the right.
When it's the more complex intervals whose errors matter to us more, we can say the tuning scheme uses complexity-weight. When, on the other hand, it's the less complex intervals, or simpler intervals, whose errors matter to us more, we can say that the tuning scheme uses simplicity-weight.[note 14] To “weight” something here means to give it importance, as in "these are weighty matters".[note 15] So a complexity-weight scheme concerns itself more with getting the complex intervals right, while a simplicity-weight scheme concerns itself more with getting the simple intervals right.
And a unity-weight scheme defines damage as absolute error (unity-weighting has no effect; it is the same as not-weighting, so we can refer to its units as "unweighted cents"). This way, it doesn't matter whether an interval is simple or complex; its error counts the same amount regardless of this.
Rationale for choosing your slope
Being diametrically opposed approaches, one might think that one way must be the correct way and the other is incorrect, but it's not actually that cut-and-dried. There are arguments for psychoacoustic plausibility either way, and some defenders of one way may tell you that the other way is straight up wrong. We (Dave and Douglas) are not here to arbitrate this theoretical disagreement; we're only here to demystify the problem and help you get the tools you need to explore it for yourself and make up your own mind.[note 16]
If we were asked which way we prefer, though, we'd suggest letting the two effects cancel each other out, and go with the thing that's easier to compute anyway: unity-weight damage.
That said, all but two of the named tuning schemes on the Xenharmonic wiki at the time of writing use simplicity-weight, and the other two use unity-weight. But just as we saw earlier with the predominance of minimax schemes, this predominance of simplicity-weight schemes is probably mostly due to the historical proliferation of named schemes which cleverly get around the need to specify a target-interval set, because being a simplicity-weight scheme is the other of the two necessary conditions to achieve that effect. And again, while these sorts of schemes have good value for consistent, reasonable, and easy-to-compute documentation of temperaments' tunings, they do not necessarily find the most practical or nicest-sounding tunings that you would want to actually use for your music. So we encourage readers to experiment and keep theorizing.
The rationale for choosing a simplicity-weight tuning scheme is perhaps more straightforward to explain than the rationale for choosing a complexity-weight tuning scheme. The idea here is that simple intervals are more important: they occur more often in music[note 17], and form the foundation of harmony that more complex chords and progressions build upon. They're more sensitive to increase in discordance with retuning. And once an interval is complex enough, it tends to sound like a mistuned version of a nearby simpler ratio, even when perfectly tuned. As Paul writes in Middle Path, "...more complex ratios are essentially insensitive to mistuning (as they are not local minima of discordance in the first place)." So, when some intervals have to be damaged, we set the maths up so that it's less okay to have errors in the simpler intervals than it is to have errors in the more complex ones. Recalling that the target-interval set is typically chosen to be a representative set of consonances (read: simple intervals), you could look at simplicity-weight tuning as a gradation of targeting; that is, you target the absolute simplest intervals like [math]\displaystyle{ \frac{3}{2} }[/math] strongly, then the almost-simplest intervals like [math]\displaystyle{ \frac{8}{5} }[/math] weakly, and past that, you just don't target at all.
The rationale for choosing a complexity-weight tuning scheme shares more in common with simplicity-weighting than you might think. Advocates of complexity-weight do not disagree that simple intervals are the most important and the most common, or that some intervals are so complex that their tuning is almost irrelevant. What is disputed is how to handle this situation. There's another couple of important facts to consider about more complex intervals:
- They are more sensitive to loss of identity by retuning, psychoacoustically—you can tune [math]\displaystyle{ \frac{2}{1} }[/math] off by maybe 20 cents and still recognize it as an octave[note 18], but if you tune [math]\displaystyle{ \frac{11}{8} }[/math] off by 20 cents the JI effect will be severely impacted; it will merely sound like a bad [math]\displaystyle{ \frac{4}{3} }[/math] or [math]\displaystyle{ \frac{7}{5} }[/math]. Complexity-weight advocates may take inspiration from the words of Harry Partch, who wrote in Genesis of a Music: "Since the importance of an identity in tonality decreases as its number increases … 11 is the weakest of the six identities of Monophony; hence the necessity for exact intonation. The bruited argument that the larger the prime number involved in the ratio of an interval the greater our license in playing the interval out of tune can lead only to music-theory idiocy. if it is not the final straw—to break the camel's tympanum—it is at least turning him into an amusiacal ninny."[note 19]
- They are also more sensitive to increase in beat-rate with retuning. For example, for the interval [math]\displaystyle{ \frac{2}{1} }[/math] it is the 2nd harmonic of the low note and the 1st harmonic of the high note that beat against one another. For the interval [math]\displaystyle{ \frac{8}{5} }[/math] it is the 8th harmonic of the low note and the 5th of the high note. Assuming the low note was 100 Hz in both cases, the beating frequencies are around 200 Hz in the first case and 800 Hz in the second case. A 9 ¢ error at 200 Hz is a 1 Hz beat. A 9 ¢ error at 800 Hz is a 4 Hz beat.
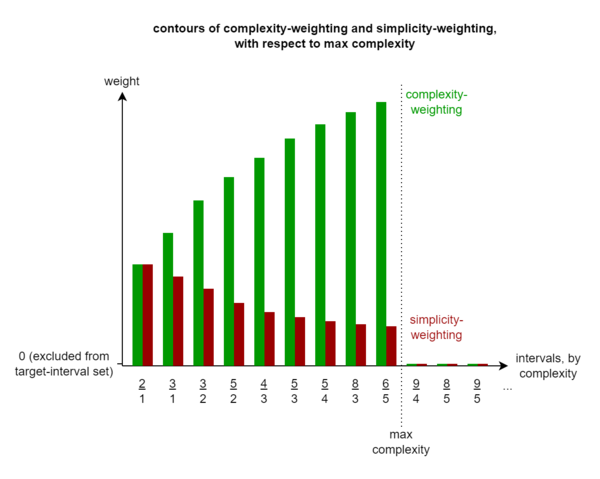
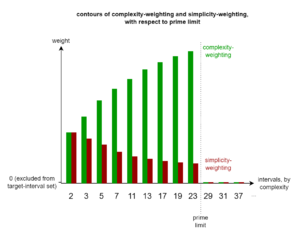
So a complexity-weight advocate will argue that the choice of target-interval set is the means by which one should set the upper bound of complexity one tunes with respect to, but then the weighting leans toward emphasizing the accuracy of anything leading up to that point. But anything past that point is not considered at all.
So to a simplicity-weighting advocate this sudden change in how you care about errors from the maximum complexity interval in your target-interval set and anything beyond may seem unnatural, but to a complexity-weight advocate the other way around might seem like a strange partial convergence in concept where instead one should tackle two important concepts, one with each lever available (lever one: target-interval set membership, and lever two: damage weight).
Terminological notes
While it may be clear from context what one means if one says one weights a target-interval, in general it is better to be clear about the fact that what one really weights is a target-interval's error, not the interval itself. This is especially important when dealing with complexity-weight damage, since the error we care most about is for the least important (weakest) intervals.
Also, note that we do not speak of "complexity-weighted damage", because it is not the damage that gets multiplied by the weight, it is the absolute error. Instead the quantity is called "complexity-weight damage" (no "-ed"), and similarly for "simplicity-weight damage" and "unity-weight damage".
Simplicity
For simplicity's sake (ha ha), we suggest that absolute error weighting should always be thought of as a multiplication, never as a division. Complexity-weighting versus simplicity-weighting is confusing enough without causing some people to second-guess themselves by worrying about whether one should multiply or divide by a quantity. Let's just keep things straightforward and always multiply.
We have found that the least confusing way to conceptualize the difference between complexity-weighting and simplicity-weighting is to always treat weighting as multiplication like this, and then to define simplicity as the reciprocal of complexity. So if [math]\displaystyle{ \frac{3}{2} }[/math]'s log-product complexity is [math]\displaystyle{ 2.585 }[/math], then its log-product simplicity is [math]\displaystyle{ \frac{1}{2.585} \approx 0.387 }[/math]. And if [math]\displaystyle{ \frac{32}{21} }[/math]'s log-product complexity is [math]\displaystyle{ 9.392 }[/math], then its log-product simplicity is [math]\displaystyle{ \frac{1}{9.392} \approx 0.106 }[/math].
So, when complexity-weighting, if [math]\displaystyle{ \frac{3}{2} }[/math] and [math]\displaystyle{ \frac{32}{21} }[/math] are both in your target-interval set, and if at some point in the optimization process they both have an absolute error of 2 ¢, and log-product complexity is your complexity function, then [math]\displaystyle{ \frac{3}{2} }[/math] incurs 2 ¢ × 2.585 (C) = 5.170 ¢(C) of damage, and [math]\displaystyle{ \frac{32}{21} }[/math] incurs 2 ¢ × 9.392 (C) = 18.785 ¢(C) of damage. Note the units of ¢(C), which can be read as "complexity-weighted cents" (we can use this name because log-product complexity is the standard complexity function; otherwise we should qualify it as "[complexity-type]-complexity-weighted cents"). You can see, then, that if we were computing a minimax tuning, that [math]\displaystyle{ \frac{3}{2} }[/math]'s damage of 5.170 ¢(C) wouldn't affect anything, while [math]\displaystyle{ \frac{32}{21} }[/math]'s damage of 18.785 ¢(C) may well make it the target-interval causing the most damage, and so the optimization procedure will seek to reduce it. And if the optimization procedure does reduces the damage to [math]\displaystyle{ \frac{32}{21} }[/math], then it will end up with less error than [math]\displaystyle{ \frac{3}{2} }[/math], since they both started out with 2 ¢ of it.[note 20]
If, on the other hand, we were simplicity-weighting, the damage to [math]\displaystyle{ \frac{3}{2} }[/math] would be 2 ¢ × 0.387 = 0.774 ¢(S) and to [math]\displaystyle{ \frac{32}{21} }[/math] would be 2 ¢ × 0.106 = 0.213 ¢(S). These units of ¢(S) can be read "simplicity-weighted cents" (again, owing to the fact that we used the standard complexity function of log-product complexity, or rather here, its reciprocal, log-product simplicity). So here we have the opposite effect. Clearly the damage to [math]\displaystyle{ \frac{3}{2} }[/math] is more likely to be caught by a optimization procedure and sought to be minimized, while the [math]\displaystyle{ \frac{32}{21} }[/math] interval's damage is not going to affect the choice of tuning nearly as much, if at all.
Weights are always non-negative.[note 21] If damage is always non-negative, and damage is possibly-weighted absolute error, and absolute error by definition is non-negative, then weight too must be non-negative.
Here's a summary table of the relationship between damage, error, weight, complexity, and simplicity:
| Value | Variable | Possible equivalences |
|---|---|---|
| Damage | [math]\displaystyle{ \mathrm{d} }[/math][note 22] | [math]\displaystyle{ |\mathrm{e}| }[/math] [math]\displaystyle{ |\mathrm{e}| × w }[/math] |
| Error | [math]\displaystyle{ \mathrm{e} }[/math] | |
| Weight | [math]\displaystyle{ w }[/math] | [math]\displaystyle{ c }[/math] [math]\displaystyle{ s }[/math] |
| Complexity | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ \frac{1}{s} }[/math] |
| Simplicity | [math]\displaystyle{ s }[/math] | [math]\displaystyle{ \frac{1}{c} }[/math] |
Example
In this section, we will introduce several new vocabulary terms and notations by way of an example. Our goal here is to find the average, RMS, and max damage of one arbitrarily chosen tuning of meantone temperament, given a particular target-interval set. Note that we're not finding the miniaverage, miniRMS, or minimax given other traits of some tuning scheme; to find any of those, we'd essentially need to repeat the following example on every possible tuning until we found the one with the smallest result for each minimization. (For detailed instructions on how to do that, see our tuning computation.)
This is akin to drawing a vertical line through tuning damage space, and finding the value of each graph—each target-interval damage graph, and each damage statistic graph (average, RMS, and max)—at the point it intersects that line.
Target-intervals
Suppose our target-interval set is the 6-TILT: [math]\displaystyle{ \left\{ \frac{2}{1}, \frac{3}{1}, \frac{3}{2}, \frac{4}{3}, \frac{5}{2}, \frac{5}{3}, \frac{5}{4}, \frac{6}{5} \right\} }[/math].
We can then set our target-interval list to be [math]\displaystyle{ \left[\frac{2}{1}, \frac{3}{1}, \frac{3}{2}, \frac{4}{3}, \frac{5}{2}, \frac{5}{3}, \frac{5}{4}, \frac{6}{5}\right] }[/math]. We use the word "list" here—as opposed to "set"—in order to suggest that the elements now have an order, because it will be important to preserve this order moving forward, so that values match up properly when we zip them up together. That's why we've used square brackets [·] to denote it rather than curly brackets {·}, since the former are conventionally used for ordered lists, while the latter are conventionally used for unordered sets.
Our target-interval list, notated as [math]\displaystyle{ \mathrm{T} }[/math], may be seen as a matrix, like so:
[math]\displaystyle{
\mathrm{T} =
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
}[/math]
This is a [math]\displaystyle{ (d, k) }[/math]-shaped matrix, which is to say:
- There are [math]\displaystyle{ d }[/math] rows where [math]\displaystyle{ d }[/math] is the dimensionality of the temperament, or in other words, the count of primes, or more generally, the count of basis elements. In this case [math]\displaystyle{ d=3 }[/math] because we're in a standard basis of a prime limit, specifically the 5-limit, where each next basis element is the next prime, and 5 is the 3rd prime.
- There are [math]\displaystyle{ k }[/math] columns where [math]\displaystyle{ k }[/math] is the target-interval count. You can think of [math]\displaystyle{ k }[/math] as standing for "kardinality" or "kount" of the target-interval list, if that helps.
We read this matrix column by column, from left to right; each column is a (prime-count) vector for the next target-interval in our list, and each of these vectors has one entry for each prime. The first column [-1 1 0⟩ is the vector for [math]\displaystyle{ \frac{3}{2} }[/math], the second column [2 -1 0⟩ is the vector for [math]\displaystyle{ \frac{4}{3} }[/math], and so on (if you skipped the previous article in this series and are wondering about the [...⟩ notation, that's Extended bra-ket notation).
(For purposes of tuning, there is no difference between the superunison and subunison versions of an interval, e.g. [math]\displaystyle{ \frac{3}{2} }[/math] and [math]\displaystyle{ \frac{2}{3} }[/math], respectively. So we'll be using superunisons throughout this series. Technically we could use undirected ratios, written with a colon, like 2:3; however, for practical purposes—in order to put interval vectors into our matrices and such—we need to just pick one direction or the other.)
Generators
In order to know what errors we're working with, we first need to state that arbitrary tuning we said we were going to be working with. We also said we were going to work with meantone temperament here. Meantone is a rank-2 temperament, and so we need to tune two generators.
Let's see how things look when we set the first generator (the period) to 1202 cents and the other generator to 698 cents. We can represent our generator tunings together in one convenient object called the generator tuning map, notated as [math]\displaystyle{ 𝒈 }[/math], and that looks like:
[math]\displaystyle{
𝒈 =
\left[ \begin{matrix}
1202 & 698 \\
\end{matrix} \right]
}[/math]
To be clear, this tuning has no special musical importance. We're not even tuning these within tenths of cents so it's certainly not intended to be an optimum tuning of any sort. It's a good enough tuning that the values we look at here won't be distractingly weird, but otherwise it's intended only as an example tuning to demonstrate these ideas with, and nothing more.
As we know, the error of an interval is the difference between its tempered size and its just size. So to find the errors of a bunch of intervals at once, we could set up a list of their tempered sizes, a corresponding list of their just sizes, and then just line up those two lists and subtract them. The result will be a list of each interval's error.
Primes
The just size list is easy, so let's get that one out of the way first. We find the just size of an interval by multiplying its vector by the just-prime tuning map or just tuning map for short, notated as [math]\displaystyle{ 𝒋 }[/math] (elsewhere you may see this called the "JIP", for "just intonation point"). For example, [math]\displaystyle{ \frac{16}{15} }[/math]'s just size is [math]\displaystyle{ \vmp{1200.000 & 1901.955 & 2786.314}{4 & -1 & -1} = 111.731 ¢ }[/math]. We can notate this as [math]\displaystyle{ 𝒋\textbf{i} = 111.731 }[/math].
[math]\displaystyle{
\begin{align}
𝒋\textbf{i}
&=
\left[ \begin{array} {ccc}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right] \left[ \begin{array} {r|r|r|r|r|r|r|r}
4 \\
{-1} \\
{-1} \\
\end{array} \right] \\[12pt]
&=
\left[ \begin{array} {rrr}
111.731 \\
\end{array} \right]
\end{align}
}[/math]
We can do the same thing with [math]\displaystyle{ 𝒋 }[/math] and [math]\displaystyle{ \mathrm{T} }[/math]. The rules of matrix multiplication allow us to do this. Because [math]\displaystyle{ 𝒋 }[/math] is a matrix with shape [math]\displaystyle{ (1, d) }[/math], we can left-multiply any matrix with [math]\displaystyle{ d }[/math] rows by it, whether that's a single interval vector like [math]\displaystyle{ \frac{16}{15} }[/math]'s [4 -1 -1⟩ with shape [math]\displaystyle{ (d, 1) }[/math], or an entire list of many target-interval vectors—such as our truncated integer limit triangle—with shape [math]\displaystyle{ (d, k) }[/math].
So let's do just that:
[math]\displaystyle{
\begin{align}
𝒋\mathrm{T}
&=
\left[ \begin{array} {ccc}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right] \left[ \begin{array} {r|r|r|r|r|r|r|r}
1 & 0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right] \\[12pt]
&=
\left[ \begin{matrix}
1200.000 & 1901.955 & 701.955 & 498.045 & 1586.310 & 884.359 & 386.314 & 315.641 \\
\end{matrix} \right]
\end{align}
}[/math]
This we could say is our target-interval (just) size list. You will probably recognize some of those familiar cents values in the end result.
Temperament
Now let's find the matching list of tempered tunings of these intervals. We've already chosen our [math]\displaystyle{ g = \monzo{1202 & 698} }[/math]. But there's no immediate way to combine this [math]\displaystyle{ (1, r) }[/math]-shaped map (where [math]\displaystyle{ r }[/math] is the rank, or count of generators) and our [math]\displaystyle{ (d, k) }[/math]-shaped target-interval list. We're missing something in between [math]\displaystyle{ r }[/math] and [math]\displaystyle{ d }[/math] to get these matrices to hook up with each other. No big deal, though; it's just our temperament's mapping, notated [math]\displaystyle{ M }[/math], which is a [math]\displaystyle{ (r, d) }[/math]-shaped matrix—after all, it is designed to gear us down from [math]\displaystyle{ d }[/math]-dimensional JI to some lower [math]\displaystyle{ r }[/math]-dimensional temperament ([math]\displaystyle{ r \leq d }[/math]). Here's the form of meantone's mapping where the first generator is an approximate octave and the second generator is an approximate fifth, which is the proper form to use given our choices of generator tunings:
[math]\displaystyle{
M =
\left[ \begin{matrix}
1 & 1 & 0 \\
0 & 1 & 4 \\
\end{matrix} \right]
}[/math]
So, combining that [math]\displaystyle{ g }[/math] with this [math]\displaystyle{ M }[/math], we get [math]\displaystyle{ 𝒈M }[/math], which is a [math]\displaystyle{ (1, \cancel{r})(\cancel{r}, d) = (1, d) }[/math]-shaped matrix, otherwise known as [math]\displaystyle{ 𝒕 }[/math], our tempered-prime tuning map or simply our "tuning map" when it's clear from the context:
[math]\displaystyle{
\begin{align}
𝒕
&=
𝒈M
\\[12pt]
&=
\left[ \begin{matrix}
1202 & 698 \\
\end{matrix} \right]
\left[ \begin{matrix}
1 & 1 & 0 \\
0 & 1 & 4 \\
\end{matrix} \right]
\\[12pt]
&=
\left[ \begin{matrix}
1202 & 1900 & 2792 \\
\end{matrix} \right]
\end{align}
}[/math]
This tells us how to tune our prime harmonics. So [math]\displaystyle{ \frac{2}{1} }[/math] is 1202 ¢, [math]\displaystyle{ \frac{3}{1} }[/math] is 1900 ¢, and [math]\displaystyle{ \frac{5}{1} }[/math] is 2792 ¢. We can find other intervals as sums and differences of these cent values. [math]\displaystyle{ \frac{5}{4} }[/math] would be [math]\displaystyle{ 2792 - (2 × 1202) = 388 }[/math] cents. In other words, it works exactly like the just-prime tuning map [math]\displaystyle{ 𝒋 }[/math], where we can multiply a vector [math]\displaystyle{ \textbf{i} }[/math] by it to get its cents value.
That means we do just like what we did with [math]\displaystyle{ 𝒋\mathrm{T} }[/math], but now using [math]\displaystyle{ 𝒕 }[/math] instead of [math]\displaystyle{ 𝒋 }[/math], so we get [math]\displaystyle{ 𝒕\mathrm{T} }[/math], which we could call our tempered target-interval size list:
[math]\displaystyle{
\begin{align}
𝒕\mathrm{T}
&=
\left[ \begin{array} {ccc}
1202 & 1900 & 2792 \\
\end{array} \right]
\left[ \begin{array} {r|r|r|r|r|r|r|r}
1 & 0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
\\[12pt]
&=
\left[ \begin{array} {rrr}
1202 & 1900 & 698 & 504 & 1590 & 892 & 388 & 310 \\
\end{array} \right]
\end{align}
}[/math]
Errors
Finally, we can find our target-interval error list, notated as [math]\displaystyle{ \textbf{e} }[/math], as the difference between these two lists:
[math]\displaystyle{
\begin{align}
\textbf{e} &= 𝒕\mathrm{T} - 𝒋\mathrm{T}
\\[12pt]
&=
\left[ \begin{array} {rrr}
1202 & 1900 & 698 & 504 & 1590 & 892 & 388 & 310 \\
\end{array} \right]
-
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 701.955 & 498.045 & 1586.310 & 884.359 & 386.314 & 315.641 \\
\end{array} \right]
\\[12pt]
&=
\left[ \begin{array} {rrr}
2.000 & {-1.955} & {-3.955} & 5.955 & 3.686 & 7.641 & 1.686 & {-5.641} \\
\end{array} \right]
\end{align}
}[/math]
Retuning map
Note that we actually have another helpful way to slice and dice this relationship. We can factor out the [math]\displaystyle{ \mathrm{T} }[/math] from [math]\displaystyle{ 𝒕\mathrm{T} - 𝒋\mathrm{T} }[/math] to express it as [math]\displaystyle{ (𝒕 - 𝒋)\mathrm{T} }[/math]. So what's special about the value in the parentheses now? Well, if [math]\displaystyle{ 𝒋 }[/math] gives the just tuning of each prime factor, and [math]\displaystyle{ 𝒕 }[/math] gives their tempered tunings, then [math]\displaystyle{ 𝒕 - 𝒋 }[/math] is the mistuning of each prime factor. But we prefer to call it the retuning map, notated as [math]\displaystyle{ 𝒓 }[/math], for two reasons:
- "Mistuning" sounds like a bad thing while this "retuning" is in the service of a greater good, and
- We want to reserve the variable name [math]\displaystyle{ 𝒎 }[/math] for the kind of map that gives us the generator counts that approximate each prime factor—a row from a mapping matrix.
But feel free to call [math]\displaystyle{ 𝒓 = 𝒕 - 𝒋 }[/math] the "mistuning map" if you prefer. [note 23]
[math]\displaystyle{
\begin{align}
𝒓 &= 𝒕 - 𝒋
\\[12pt]
&=
\left[ \begin{array} {rrr}
1202 & 1900 & 2792 \\
\end{array} \right] -
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\\[12pt]
&=
\left[ \begin{array} {rrr}
2.000 & {-1.955} & 5.686 \\
\end{array} \right]
\end{align}
}[/math]
So we've seen in the previous subsection that we can find the target-interval error list as the difference between the two lists [math]\displaystyle{ 𝒕\mathrm{T} }[/math] and [math]\displaystyle{ 𝒋\mathrm{T} }[/math], but if this way of thinking clicks better for you, know that you can alternatively find the target-interval error list [math]\displaystyle{ \textbf{e} }[/math] as the product of [math]\displaystyle{ 𝒓 }[/math] and [math]\displaystyle{ \mathrm{T} }[/math]:
[math]\displaystyle{
\begin{align}
\textbf{e} &= 𝒓\mathrm{T}
\\[12pt]
&=
\left[ \begin{array} {rrr}
2.000 & {-1.955} & 5.686 \\
\end{array} \right]
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
\\[12pt]
&=
\left[ \begin{array} {rrr}
2.000 & {-1.955} & {-3.955} & 5.955 & 3.686 & 7.641 & 1.686 & {-5.641} \\
\end{array} \right]
\end{align}
}[/math]
In general, you can find the error of any interval with [math]\displaystyle{ 𝒓\textbf{i} }[/math]. In other words, tuning maps give interval size ([math]\displaystyle{ 𝒕\textbf{i} }[/math] or [math]\displaystyle{ 𝒋\textbf{i} }[/math]), but the retuning map gives interval error; either way the interval has units of p, the maps have units of ¢/p, and the result has units of ¢.
Absolute errors
Either way we approach our target-interval error list—as [math]\displaystyle{ 𝒕\mathrm{T} - 𝒋\mathrm{T} }[/math], or as [math]\displaystyle{ 𝒓\mathrm{T} }[/math]—we find the same result. And so the absolute valued version of that, called our target-interval absolute error list and notated as [math]\displaystyle{ |\textbf{e}| }[/math], would look like this:
[math]\displaystyle{
|\textbf{e}| =
\left[ \begin{array} {rrr}
2.000 & 1.955 & 3.955 & 5.955 & 3.686 & 7.641 & 1.686 & 5.641 \\
\end{array} \right]
}[/math]
That is, we've just removed any negative signs. That's all. And if we were using unity-weight damage, then our target-interval damage list, notated as [math]\displaystyle{ \textbf{d} }[/math], would be equivalent to that, that is [math]\displaystyle{ \textbf{d} = |\textbf{e}| }[/math].
A comment on notation: Placing single vertical bars around a scalar is universally recognised as taking its absolute value, so we think the obvious meaning of single vertical bars around a vector is its entry-wise absolute value, that is, taking the absolute value of each entry. That's what we're doing here. But you may find other authors using [math]\displaystyle{ |\textbf{v}| }[/math] to take the "magnitude" or 2-norm of a vector. We think this is an abuse of notation, since we have the double-bar notation [math]\displaystyle{ ‖\textbf{v}‖ }[/math] or [math]\displaystyle{ ‖\textbf{v}‖_2 }[/math] for the 2-norm.
Weight matrix
But suppose we are using a complexity-weight tuning scheme. In that case, the relationship between [math]\displaystyle{ \textbf{d} }[/math] and [math]\displaystyle{ \textbf{e} }[/math] is slightly more complicated. We would say [math]\displaystyle{ \textbf{d} = |\textbf{e}|W }[/math], where [math]\displaystyle{ W }[/math] is our target-interval weight matrix. Here's what that might look like:
[math]\displaystyle{
W =
\left[ \begin{matrix}
1.000 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1.585 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 2.585 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 3.585 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 3.322 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 3.907 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 4.322 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 4.907 \\
\end{matrix} \right]
}[/math]
This now is a [math]\displaystyle{ (k, k) }[/math]-shaped matrix, with one row and one column for each target-interval. You'll also notice that it's a diagonal matrix, where every entry is zero except the entries along the main diagonal. You may wonder, then, why this information is not simply represented in a list. The reason has to do with the mechanics of linear algebra, in particular, again, how matrix multiplication works. When two lists of numbers are multiplied as matrices, one is oriented as a row and the other as a column, and the result is a single value, or scalar; this is because a [math]\displaystyle{ (1, n) }[/math]-shaped matrix times an [math]\displaystyle{ (n, 1) }[/math]-shaped matrix is a [math]\displaystyle{ (1, \cancel{n})(\cancel{n}, 1) = (1, 1) }[/math]-shaped matrix, which is essentially a scalar. So while when we have two vectors [math]\displaystyle{ \textbf{v}_1 }[/math] and [math]\displaystyle{ \textbf{v}_2 }[/math] and our goal is the vector where each entry is the difference of the matching entries of the two vectors, it is as simple as [math]\displaystyle{ \textbf{v}_1 - \textbf{v}_2 }[/math] (as we saw with [math]\displaystyle{ \textbf{e} = 𝒕\mathrm{T} - 𝒋\mathrm{T} }[/math]), but it's not that simple with multiplication.[note 24] If the goal is to find the vector where each item of [math]\displaystyle{ \textbf{v}_1 }[/math] is multiplied by the corresponding item of [math]\displaystyle{ \textbf{v}_2 }[/math]—and we could call this the entry-wise product—the simplest way is to diagonalize one list. If you think about it in terms of matrix shape, you can see that if you want a [math]\displaystyle{ (1, n) }[/math] vector to stay a [math]\displaystyle{ (1, n) }[/math] vector, then you'll need to multiply it not by another [math]\displaystyle{ (n, 1) }[/math] vector, but by a square [math]\displaystyle{ (n, n) }[/math] matrix.
So what we do in RTT is take a target-interval weight list, notated as [math]\displaystyle{ 𝒘 }[/math], and turn it into a diagonal matrix, [math]\displaystyle{ W }[/math]:
[math]\displaystyle{
\begin{align}
W &= \text{diag}(𝒘)
\\[12pt]
&=
\text{diag}\left(
\left[ \begin{matrix}
1.000 & 1.585 & 2.585 & 3.585 & 3.322 & 3.907 & 4.322 & 4.907 \\
\end{matrix} \right]
\right)
\\[12pt]
&=
\left[ \begin{matrix}
1.000 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1.585 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 2.585 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 3.585 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 3.322 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 3.907 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 4.322 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 4.907 \\
\end{matrix} \right]
\end{align}
}[/math]
As for the actual entries here, these are just the log-product complexities of the target-intervals. You'll recognize 2.585 as the log-product complexity of [math]\displaystyle{ \frac{3}{2} }[/math], and the log-product complexity of [math]\displaystyle{ \frac{4}{3} }[/math] can be seen to be exactly 1 more than that; this is explained because it has the same prime factors as [math]\displaystyle{ \frac{3}{2} }[/math] with the addition of another prime 2, which adds 1 to the complexity because [math]\displaystyle{ \log_2{2} = 1 }[/math]. So 4.322 is the complexity of [math]\displaystyle{ \frac{5}{4} }[/math], 3.322 is the complexity of [math]\displaystyle{ \frac{5}{2} }[/math], and so on.
Complexity-weight damage
The values in our weight matrix [math]\displaystyle{ W }[/math] are complexities. In other words, we are using a complexity-weight damage. It may be preferable for us to refer to our weight matrix as [math]\displaystyle{ C }[/math] now, rather than the generic [math]\displaystyle{ W }[/math], in order to remind us that we are complexity-weighting our error (and of course, had we simplicity-weighted it instead, we could use [math]\displaystyle{ S }[/math] in place of [math]\displaystyle{ W }[/math]).
And so now we can find our target-interval damage list [math]\displaystyle{ \textbf{d} }[/math] as [math]\displaystyle{ |\textbf{e}|C }[/math]:
[math]\displaystyle{
\begin{align}
\textbf{d} &= |\textbf{e}|C
\\[12pt]
&=
\left[ \begin{array} {rrr}
2.000 & 1.955 & 3.955 & 5.955 & 3.686 & 7.641 & 1.686 & 5.641 \\
\end{array} \right]
\left[ \begin{array} {rrr}
1.000 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1.585 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 2.585 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 3.585 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 3.322 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 3.907 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 4.322 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 4.907 \\
\end{array} \right]
\\[12pt]
&=
\left[ \begin{array} {rrr}
2.000 & 3.099 & 10.224 & 21.349 & 12.245 & 29.853 & 7.287 & 27.680 \\
\end{array} \right]
\end{align}
}[/math]
Power means
So now finally let's evaluate some power means for this tuning. In particular, let's check the three optimization powers we've found to be most noteworthy: [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], and [math]\displaystyle{ ∞ }[/math].
If we were to evaluate the [math]\displaystyle{ 1 }[/math]-mean here we'd get:
[math]\displaystyle{
\begin{align}
\llangle\textbf{d}\rrangle_1
&=
\sqrt[1]{\strut \dfrac{\sum\limits_{n=1}^k d_n^1}{k}}
\\
&=
\sqrt[1]{\rule[15pt]{0pt}{0pt} \dfrac{2.000^1 + 3.099^1 + 10.224^1 + 21.349^1 + 12.245^1 + 29.853^1 + 7.287^1 + 27.680^1}{8}}
\\
&=
14.217
\end{align}
}[/math]
The [math]\displaystyle{ 2 }[/math]-mean:
[math]\displaystyle{
\begin{align}
\llangle\textbf{d}\rrangle_2
&=
\sqrt[2]{\strut \dfrac{\sum\limits_{n=1}^k d_n^2}{k}}
\\
&=
\sqrt[2]{\rule[15pt]{0pt}{0pt} \dfrac{2.000^2 + 3.099^2 + 10.224^2 + 21.349^2 + 12.245^2 + 29.853^2 + 7.287^2 + 27.680^2}{8}}
\\
&=
6.167
\end{align}
}[/math]
and the [math]\displaystyle{ ∞ }[/math]-mean:
[math]\displaystyle{
\begin{align}
\llangle\textbf{d}\rrangle_∞
&=
\sqrt[∞]{\strut \dfrac{\sum\limits_{n=1}^k d_n^∞}{k}}
\\
&=
\sqrt[∞]{\rule[15pt]{0pt}{0pt} \dfrac{2.000^∞ + 3.099^∞ + 10.224^∞ + 21.349^∞ + 12.245^∞ + 29.853^∞ + 7.287^∞ + 27.680^∞}{8}}
\\
&=
\max(2.000, 3.099, 10.224, 21.349, 12.245, 29.853, 7.287, 27.680)
\\
&=
29.853
\end{align}
}[/math]
Thus concludes our example, showing how we might find the value of each damage statistic graph along a vertical line through tuning damage space, i.e. the line corresponding to a single arbitrary tuning in that space.
Target-intervals
Up to this point, we've only looked at a single target-interval set: the truncated 6-integer-limit triangle[note 25] (that's the "6-TILT" for short). But this is not the only viable choice. So let's unpack this trait of tuning schemes in more detail now.
Target-interval set schemes
Unlike optimization power and damage weight slope, the possibilities for your target-interval set are significantly more open-ended. We have just three optimization powers (technically a continuum, but few people use the powers between [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], and [math]\displaystyle{ ∞ }[/math]), and just three weight slopes, but a large number of possible combinations of target-intervals.
Also, it's unlikely that a person will switch optimization power and weight slope from one temperament to the next, or from one song to the next. More likely, they will make up their mind about a certain combination of optimization power and weight slope—the one that makes musical and/or philosophical sense to them—and just use it for everything. This is not so for target-intervals, however. These, like temperaments, depend very much on the particularities of the music, or instrument, being tuned for.
We've mentioned that some tuning schemes allow you to get around the need to specify your target-interval set. This is one extreme—caring very little about which intervals are considered most carefully by the tuning process. At the other extreme, a person might hand-pick their target-interval set for each temperament, or each individual song they write. That's caring as much as possible about which intervals are tuned for. In the middle ground we have things called target-interval set schemes. If a "tuning scheme" is a set of rules to follow to find a tuning for a given temperament, then a "target-interval set scheme" is a set of rules to follow to find a target-interval set for a temperament (which would then be used as part of a tuning scheme to find a tuning for that temperament). So if you do care about which intervals should be tuned for, but not in any particular way beyond trusting what experts think they should be for a given temperament (prime limit, really), then a set scheme is what you want to use.
In this section, we won't be attempting to exhaust all possibilities of reasonable target-interval set schemes. Instead, we're just going to cover a couple of the most common historical ones, as well as talk through our rationale for the set scheme we developed in response to them (and recommend over them). If you have doubts about our suggestions, please explore on your own and figure out what set scheme best suits your music. You might even find that set schemes aren't for you and you'd rather hand-pick per piece.
The importance of exclusivity
But before we get into specific examples of target-interval set schemes, let's take a moment to touch upon a concept of fundamental importance when it comes to such sets: it's important to think of them as somewhat exclusive. This is because each new interval you permit into your set reduces the chances for reducing the damage to every other interval that was already in the set, and can only risk increasing the overall damage to the set per the chosen power minimum. We could make an analogy where damage reduction is like a funding pool; we don't have infinite money to distribute grants to all the deserving artists, so we must ensure that the few who receive the money need and/or deserve it the most. In practical terms, what this means is that the selection of a target-interval set is not as simple as remembering every interval you care about; it's more of a delicate balancing act of choosing the most important intervals—nothing more, and nothing less.
Let's look at an example where adding a new interval to the target-interval set dramatically impacts the amount of damage to existing members. Suppose we're tuning magic temperament, and we choose that 6-TILT as our target-interval set, and let's say we're going with a unity-weight minimax scheme. That'll lead to the tuning ⟨1204.936 381.378], with the following damage list:
[math]\displaystyle{
\begin{array} {lcccccccccccccccccc}
& & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\
\textbf{d} & = & \left[\right. & 4.936 & 4.936 & 0.000 & 4.936 & 0.000 & 0.000 & 4.936 & 4.936 & \left.\right] \\
\end{array}
}[/math]
Here we can see we've made the error to primes 2, 3 and 5 equal, so we end up with them canceling out to a pure [math]\displaystyle{ \frac{3}{2} }[/math], [math]\displaystyle{ \frac{5}{2} }[/math], and [math]\displaystyle{ \frac{5}{3} }[/math], without doing any more than that amount of damage to any other interval in our set.
But what happens if we add [math]\displaystyle{ \frac{8}{5} }[/math] to our target-interval set, though—our first interval with more than two prime factors on one side of the fraction bar? Well, all else the same, we instead find a tuning ⟨1200.000 380.391], with damage list:
[math]\displaystyle{
\begin{array} {lccccccccccccccc}
& & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} & \frac{8}{5} \\
\textbf{d} & = & \left[\right. & 0.000 & 0.000 & 0.000 & 0.000 & 5.923 & 5.923 & 5.923 & 5.923 & 5.923 & \left.\right] \\
\end{array}
}[/math]
Having all of those factors of 2 in one place (the numerator of [math]\displaystyle{ \frac{8}{5} }[/math]) has led to this tuning zeroing out the damage to prime 2, and from there it settled on zero damage to prime 3 as well; while this has resulted in zero damage to any intervals with no factors of 5, remember that this is a minimax tuning, following the logic that a tuning is only as good as its weakest link(s), and notice that for all of our intervals with factors of 5, the damage to them has gone up to a new higher maximum of 5.923. So unless we know that the interval [math]\displaystyle{ \frac{8}{5} }[/math] is of major importance in the music to be performed, we may not want to include it in our target-interval set.
And we can also witness an important thing about target-intervals in this example: we target their damages for minimization, meaning we aim for zero, but we can’t always hit it.
The importance of representing every prime
Whatever target-interval set one picks, it's important for each prime within the prime-limit to be included as a prime factor in at least one target-interval. This means, for example, that it would be improper to tune a 5-limit temperament with a target-interval set which only included [math]\displaystyle{ \left\{\frac{2}{1}, \frac{3}{1}, \frac{3}{2}, \frac{4}{3}, \frac{8}{3}, \frac{9}{4}\right\} }[/math], because nowhere in any of those target-intervals do we find any factors of 5. This leaves us with insufficient information to properly optimize the tuning, in particular how to tune the tempered version of prime 5.
As a human asked to perform such an optimization, we might feel safe to fill in this blank with the obvious assumption that the tuning of prime 5 should be left alone, that is, that we should keep prime 5 tuned justly. On the other hand, if we asked a computer to perform such an optimization, depending on how "dumb" the algorithms it uses are, it might just crash trying to figure out what to do with prime 5.
There's no particular reason anyone would want to completely leave a prime out of their target-interval set. We mention here only as something to watch out for.
Only the primes
One of the most common mistakes people—especially beginners—make when choosing a target-interval set is to choose the primes being tempered, and nothing else. This might seem at first like a logical choice, but it overlooks much of the typical musical reality:
- It's naïve, taking no account of whether the prime errors (yes, their errors, not their damage; that is, the amounts before taking their absolute value) tend to cancel each other out or to reinforce each other when these primes are found combined together in the simple ratios that most likely constitute the actual harmonic material of the music.
- It makes no account of the fact that in consonant ratios we tend to find higher powers of prime 2's than other primes.
- Already upon reaching the third prime, prime 5, the intervals ([math]\displaystyle{ \frac{5}{1} }[/math], [math]\displaystyle{ \frac{7}{1} }[/math], ...) have gotten so wide that with typical timbres they are not dissonant no matter how inaccurately they are tuned.
So unless the musical piece we're going to perform is nothing but runs up and down a tempered version of the harmonic series, tuning only to the primes probably isn't going to be our ideal tuning. Targeting only the primes is certainly good for some theoretical and documentation purposes (more on this at the end of this section), but it has no relevance for human psychoacoustics, and therefore low validity for use in music itself.
For an illustrative example, we'll look at the ⟨17 27 40] map for 17-ET. We'll consider the damages to intervals in a set that has been designed to represent musical reality well. Such a set includes [math]\displaystyle{ \frac{2}{1} }[/math] and [math]\displaystyle{ \frac{3}{1} }[/math], of course, but it includes many other intervals too. And notably it does not include [math]\displaystyle{ \frac{5}{1} }[/math], which is too large; instead it includes its close cousins like [math]\displaystyle{ \frac{5}{2} }[/math] and [math]\displaystyle{ \frac{5}{4} }[/math]. In particular we'll be using the 6-TILT, the target-interval set that we've been referencing on occasion throughout this article. Also, we'll use a minimax tuning with unity-weight damage, though those choices are not central to the point this example is making.
So first, here is our damage list when we tune with respect to it:
[math]\displaystyle{
\begin{array} {lccccccccccccccccccccccccccc}
& & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\
\textbf{d} & = & [ & 6.668 & 6.663 & 0.005 & 6.673 & 28.194 & 28.189 & 34.862 & 34.862 & ] \\[12pt]
\llangle\textbf{d}\rrangle_∞ & = & & 34.862 \\
\end{array}
}[/math]
And for comparison, here is the list of damages to the same intervals, but when they've been tuned using a target-interval set that includes only the primes, which we'll distinguish with a subscript 'p' for "primes-only", as [math]\displaystyle{ \textbf{d}_{\text{p}} }[/math]:
[math]\displaystyle{
\begin{array} {lccccccccccccccccccccccccccc}
& & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\
\textbf{d}_{\text{p}} & = & [ & 10.442 & 12.657 & 2.215 & 8.227 & 23.088 & 25.303 & 33.530 & 35.745 & ] \\[12pt]
\llangle\textbf{d}_{\text{p}}\rrangle_∞ & = & & 35.745 \\
\end{array}
}[/math]
Notice first that according to our chosen optimization power of [math]\displaystyle{ ∞ }[/math], the tuning that targets the 6-TILT is preferred, because it has the lower maximum damage to any one interval: 34.862 versus the primes-only tuning's 35.745.[note 26] Next notice that for both of these tunings, the interval dealt the maximum damage is the last one, [math]\displaystyle{ \frac{6}{5} }[/math]. This makes sense because—in either one of these tunings—both prime 2 and prime 3 are tuned narrow, so when they are on opposite sides of the fraction bar, their errors cancel out (as they do in [math]\displaystyle{ \frac{3}{2} }[/math], resulting in an almost pure tuning because the errors also happen to be almost exactly the same amount), while when they are on the same side of the fraction bar as they are in [math]\displaystyle{ \frac{6}{5} }[/math], they reinforce each other, so the total error increases. Furthermore, with prime 5 tuned wide in either tuning, and it being on the opposite side of the fraction bar from primes 2 and 3 in [math]\displaystyle{ \frac{6}{5} }[/math], the error compounds even more. In order to minimize this maximum damage, then, what the 6-TILT tuning did to optimize itself was deal more damage to prime 5 itself, because it found that by doing so, it could actually reduce the damage where it most mattered, on interval [math]\displaystyle{ \frac{6}{5} }[/math]. Tuning only to the primes would never compromise on prime 5 like that, even though the interval [math]\displaystyle{ \frac{5}{1} }[/math] is less sensitive to mistuning.
We should say before moving on that despite the limitations of targeting only the primes' damages for minimization, all but two of the tuning schemes named on the Xenharmonic wiki at the time of writing seemingly do just that. But as we saw earlier with the predominance of minimax and simplicity-weight schemes, this predominance of seemingly prime-targeting schemes is probably mostly due to the historical proliferation of named schemes which cleverly get around the need to specify a target-interval set. But wait, you may ask: how could a scheme have no target-interval set at all, and yet (seemingly) target only the primes? Well, in order to understand that, we'll have to go into detail about what exactly we mean by these schemes "seemingly" targeting the primes (not really targeting them), and that sort of explanation is beyond the scope of this article. For now we can at least say that these schemes target all intervals, but indirectly, by targeting the primes (and as stated previously, this requires two conditions: that it be a minimax tuning scheme, and that it uses simplicity-weight damage). You can look forward to a full explanation of this idea later, in the all-interval tuning schemes article. For now, let's just state again that while these sorts of all-interval tuning schemes have good value for consistent, reasonable, and easy-to-compute documentation of temperaments' tunings, they do not necessarily produce the most practical or nicest-sounding tunings that you would want to actually use for your music, in particular noting how they may not do the best job at minimizing damage to the actual consonances used in music.[note 27]
Odd limit diamond (OLD)
The first useful target-interval set scheme we'll be looking at is the "'odd limit diamond'" or tonality diamond, as used for the historical tunings described on the Target tunings page. The initials for that name are OLD, and so we can maybe see why the authors of that article didn't opt for initializing it themselves. On the other hand, since we believe this set scheme has been outmoded by our own development—the truncated integer limit triangle—we're cheekily okay with that initialism.
The odd limit diamond was popularized in the writings of Harry Partch. Partch used it as a set of pitch classes and as an instrument layout (a kind of keyboard layout), but here we’re concerned with its use as a set of target-intervals. We'll begin by deriving Partch's keyboard layout of pitches, which may be familiar to many readers, and from there we'll derive the target-interval set.
Derivation of the keyboard layout
To review, an odd limit diamond lays out all the odd numbers up to some odd limit along a horizontal axis, and the same list of odd numbers along a vertical axis, then fills in this grid using the horizontal axis as numerators and the vertical axis as denominators. As we go, let's work through a 9-odd-limit example:
1 3 5 7 9 1 1/1 3/1 5/1 7/1 9/1 3 1/3 3/3 5/3 7/3 9/3 5 1/5 3/5 5/5 7/5 9/5 7 1/7 3/7 5/7 7/7 9/7 9 1/9 3/9 5/9 7/9 9/9
All ratios are then put into lowest terms, which results in things like [math]\displaystyle{ \frac{9}{3} }[/math] reducing to [math]\displaystyle{ \frac{3}{1} }[/math], and notably the entire main diagonal reduces to a string of [math]\displaystyle{ \frac{1}{1} }[/math] unisons.
1 3 5 7 9 1 1/1 3/1 5/1 7/1 9/1 3 1/3 1/1 5/3 7/3 3/1 5 1/5 3/5 1/1 7/5 9/5 7 1/7 3/7 5/7 1/1 9/7 9 1/9 1/3 5/9 7/9 1/1
The whole thing then gets tilted so that this main diagonal becomes a vertical line, and the original square becomes a diamond—hence the name. We can drop the axis labels too, at this point.
1/1
1/3 3/1
1/5 1/1 5/1
1/7 3/5 5/3 7/1
1/9 3/7 1/1 7/3 9/1
1/3 5/7 7/5 3/1
5/9 1/1 9/5
7/9 9/7
1/1
Next, all intervals are octave reduced (factors of 2 are added to the numerator or denominator until the ratio is between 1 inclusive and 2 exclusive); this decreases the size of most intervals on the right half, and increases the size of most intervals on the left half.
1/1
4/3 3/2
8/5 1/1 5/4
8/7 6/5 5/3 7/4
16/9 12/7 1/1 7/6 9/8
4/3 10/7 7/5 3/2
10/9 1/1 9/5
14/9 9/7
1/1
This is what an odd limit diamond or tonality diamond, specifically the 9-odd limit diamond, looks like when used as a kind of keyboard layout.[note 28] But we're really after an understanding of an odd limit diamond when used as a target-interval set.
Derivation of target-interval set
The next thing we do is replace the unisons with octaves. For the keyboard layout, the unisons are all quite useful. Those unisons are strategically located so that all transpositions of any given chord can be played anywhere within the bounds of the diamond without changing the shape formed by the keys required to produce it. But when using these ratios as a target-interval set, there's no sense including unisons; if our [math]\displaystyle{ \frac{1}{1} }[/math] is not tuned pure, then we may need to rethink our music on a deeper philosophical level than this article on RTT tuning is prepared to contend with! The tuning of [math]\displaystyle{ \frac{2}{1} }[/math], on the other hand, tends to be of utmost importance.
The two tunings described on the Target tunings page of the wiki happen to both enforce pure octaves. To avoid getting into the weeds about the way the algorithms are described there, we can say here that they essentially put [math]\displaystyle{ \frac{2}{1} }[/math] into their held-interval basis instead of their target-interval set. If we were to use the odd limit diamond as our target-interval set for a tempered-octave tuning scheme, however, we'd want to make sure the octave at least ended up in our target-interval set; that is, we may not need the octave's damage to go all the way to zero, but surely we at least care about it staying small. And since including the octave in the target-interval set in the case of a pure-octave tuning scheme makes no difference, we believe the most generally practical suggestion here, to cover both cases, is to think of the odd limit diamond as including [math]\displaystyle{ \frac{2}{1} }[/math] when used as a target-interval set. There's even a logical way to think about this [math]\displaystyle{ \frac{2}{1} }[/math] as the way to octave reduce [math]\displaystyle{ \frac{1}{1} }[/math] in the domain of intervals, as we use for tuning, i.e. that the range pitches are octave-reduced to is [math]\displaystyle{ \frac{1}{1} \leq \frac{n}{d} \lt \frac{2}{1} }[/math] while the range intervals are octave-reduced to is [math]\displaystyle{ \frac{1}{1} \lt \frac{n}{d} \leq \frac{2}{1} }[/math] (note how the [math]\displaystyle{ \lt }[/math] and [math]\displaystyle{ \leq }[/math] are in different positions in the two inequalities).
This all said, we still think that our truncated integer limit triangle is a superior choice of a target-interval set scheme, particularly for tempered-octave tuning schemes, but also for pure-octave schemes. But we'll hold off on getting into detail about why that is until later, at the end of the section on our own scheme.
So back to the odd limit diamond, then, here's what our diamond looks like with the unisons octave-reduced to [math]\displaystyle{ \frac{2}{1} }[/math]:
2/1
4/3 3/2
8/5 2/1 5/4
8/7 6/5 5/3 7/4
16/9 12/7 2/1 7/6 9/8
4/3 10/7 7/5 3/2
10/9 2/1 9/5
14/9 9/7
2/1
Next up, the second key difference between the keyboard layout and the target-interval set is that the former includes duplicate ratios, whereas the latter does not. This makes it a "set" in the mathematical sense, rather than a "multiset" like the keyboard layout.[note 29] For the 9-odd limit diamond, this de-duping only results in the combinations of 3 and 9 getting eliminated (i.e. we eliminate the extra [math]\displaystyle{ \frac{3}{2} }[/math] and [math]\displaystyle{ \frac{4}{3} }[/math] that resulted from [math]\displaystyle{ \frac{9}{3} }[/math] reducing to [math]\displaystyle{ \frac{3}{1} }[/math] and [math]\displaystyle{ \frac{3}{9} }[/math] reducing to [math]\displaystyle{ \frac{1}{3} }[/math], respectively), and of course all but the first of that vertical line of [math]\displaystyle{ \frac{2}{1} }[/math]'s getting eliminated:
2/1
4/3 3/2
8/5 5/4
8/7 6/5 5/3 7/4
16/9 12/7 7/6 9/8
10/7 7/5
10/9 9/5
14/9 9/7
And that's all there is to finding an odd limit diamond target-interval set.
So the 9-odd limit diamond is: [math]\displaystyle{ \left\{ \frac{2}{1}, \frac{3}{2}, \frac{4}{3}, \frac{5}{4}, \frac{8}{5}, \frac{5}{3}, \frac{6}{5}, \frac{7}{4}, \frac{8}{7}, \frac{7}{6}, \frac{12}{7}, \frac{7}{5}, \frac{10}{7}, \frac{9}{8}, \frac{16}{9}, \frac{9}{5}, \frac{10}{9}, \frac{9}{7}, \frac{14}{9} \right\} }[/math]. That's a total of 19 target-intervals.
Pitches vs. intervals
We again note that using the ratios of an odd limit diamond as pitches (or pitch classes), is very different from using them as intervals. For example, a Partchian performer with a physical diamond in front of them can bang the [math]\displaystyle{ \frac{3}{2} }[/math] key and the [math]\displaystyle{ \frac{5}{3} }[/math] key at once, producing a [math]\displaystyle{ \frac{10}{9} }[/math] interval between them. But the presence of [math]\displaystyle{ \frac{3}{2} }[/math] and [math]\displaystyle{ \frac{5}{3} }[/math] in a target-interval set does not imply that [math]\displaystyle{ \frac{10}{9} }[/math] is also a member.
Choosing the odd limit (its default value given a temperament)
But more does remain to be answered. First: how might we choose the odd limit programmatically for a given temperament?
The typical choice of odd limit is the largest one possible within the prime limit of your temperament. In other words, find your prime limit, then find the next prime after that prime, and subtract 2 from that, and that should be your odd limit. This gives you the longest sequence of odd numbers with no gaps to be found at the given prime limit. In other words, it gives you the largest odd limit at the given prime limit. Why settle for less?
In the case of a 5(-prime)-limit temperament, this works out so that the odd limit of the diamond is the same as the prime limit of the temperament; this is because the next odd number above prime 5 is also a prime: it is prime 7. But in the case of a 7-limit temperament, the odd limit of its typical diamond is not also equal to 7, because the next odd after 7 is 9. The next prime limit doesn't begin until 11, so the typical odd limit diamond chosen for 7-limit temperaments is the 9-odd limit diamond. That said, it's not ridiculous in the 7-prime-limit case to wish to exclude intervals with 9's in them by tuning to the 7-odd limit diamond instead; but if you want that, it's probably best to specify it.
Truncated integer limit triangle (TILT)
As we developed this tuning article series, we found the existing theory around target-interval sets somewhat lacking, and ended up conducting some original research ourselves. Enter the truncated integer limit triangle, or TILT for short. It took us months to come up with a target-interval set scheme that we were both satisfied with. Perhaps the old OLDs are so entrenched that we're tilting at windmills with our TILTs, but we hope you will find our result appealing. In any case, you are very free to steal any or all of our ideas, and adapt them to whatever scheme you'd prefer.
First of all, our triangle gives no special treatment to prime 2, so it includes even numbers as well as odd, or in other words, integers, and accordingly is specified by an integer limit rather than an odd limit (as per the name). Also, we truncate our integer limit triangle, by which we mean that we eliminate intervals that are too large, too small, or too complex to worry about tuning; so it is truncated both in the geometric sense as it appears on the triangle as well as in the sense of interval size.
We predict that the integer limit part of our scheme will strike most readers as a perfectly logical solution to a cut-and-dried problem. On the other hand, truncation is a messier problem, so readers should be more likely to not exactly agree with our final choices there, which were size between [math]\displaystyle{ \frac{15}{13} }[/math] and [math]\displaystyle{ \frac{13}{4} }[/math] (inclusive on both sides), and product complexity less than or equal to 13 times the integer limit. So to be clear, we recognize that these are somewhat arbitrary rules, and won't spend too much time justifying these; again, please define your own exact bounds if you find ours don't fit your needs. In any case, we'll look at all of our choices in more detail below.
Integer limit
Suppose we're using a 7-(prime-)limit temperament. The next prime after 7 is 11. With the odd limit diamond our default programmatic choice of odd limit was the odd just before the next prime, which in this case would be 9. But for the truncated integer limit triangle, our programmatic choice should be the integer just before this next prime, which in this case would be 10.[note 30] In other words, we're looking for the largest integer limit within the given prime limit, so for prime limit 7, that's integer limit 10.
The formula for this integer limit, then, would be:
[math]\displaystyle{
\text{default_integer_limit} = \text{p}(\pi(p)+1)-1
}[/math]
where [math]\displaystyle{ p }[/math] is the prime limit, [math]\displaystyle{ \pi(p) }[/math] is the index of prime [math]\displaystyle{ p }[/math], and [math]\displaystyle{ \text{p}(i) }[/math] is the [math]\displaystyle{ i }[/math]th prime.
Here's an integer triangle for integer limit 10, and we've seen no particular need to rotate the thing 45° as is done with traditional tonality diamonds. Also, we haven't even bothered to fill in anything besides ratios for superunison intervals; this is what makes it a triangle rather than a diamond:
1 2 3 4 5 6 7 8 9 10 1 2/1 3/1 4/1 5/1 6/1 7/1 8/1 9/1 10/1 2 3/2 4/2 5/2 6/2 7/2 8/2 9/2 10/2 3 4/3 5/3 6/3 7/3 8/3 9/3 10/3 4 5/4 6/4 7/4 8/4 9/4 10/4 5 6/5 7/5 8/5 9/5 10/5 6 7/6 8/6 9/6 10/6 7 8/7 9/7 10/7 8 9/8 10/8 9 10/9 10
Min size truncation
The first part of our truncation process we'll apply is the minimum size truncation.
When constructing a truncated integer limit triangle, we only include superunison intervals, but not the smallest ones. Specifically, we exclude all intervals that are smaller than [math]\displaystyle{ \frac{15}{13} }[/math], which is approximately 247.741 ¢.[note 31] This cutoff is designed to fall at right about the boundary between two conventional diatonic general interval size categories: seconds and thirds. The effect is that thirds are allowed into the target-interval set, while seconds are excluded.
Regarding the choice of excluding seconds and smaller:
- While seconds are very important in melody, they are not as important in harmony, meaning that they don't often appear in chords; a glance at Wikipedia's "list of chords" support this.
- And you have to ask, when they do appear, are they functioning as consonances, i.e. approximations of simple ratios, or as dissonances that need to be resolved? Typically it is the latter.
- Furthermore, a melodic JND is far larger than a harmonic JND; A melodic JND is about 10 ¢, while a harmonic JND is only about 3 ¢. Of course these numbers depend on context and who you ask, but most will agree melody is far more tolerant of errors.[note 32]
- And even when people have strong feelings about the ideal tuning of melodic intervals, it tends to have little to do with ratios, simple or otherwise.
We can also point to some psychoacoustic theory on why (simultaneous) seconds are relatively dissonant no matter how you tune them. The magic words are "critical band" roughness. Put very crudely: Our ears have a series of overlapping "frequency buckets" and if two tones fall in the same frequency bucket they are dissonant (because we can't quite distinguish them), unless they are so close together in frequency that they are perceived as a single tone varying periodically in loudness. If they fall in different buckets they are not dissonant, except they are partially dissonant when some of their harmonics fall in the same bucket, unless those harmonics are so close together in frequency that they are perceived as a single harmonic varying periodically in loudness. Of course there are not really such sharp cutoffs. It's all very fuzzy.
The approximate spacing of the buckets in Hz, in the vicinity of a frequency [math]\displaystyle{ f }[/math] (in Hz) is given by
[math]\displaystyle{ \text{ERB}(f) = 24.7 × \left(\frac{4.37f}{1000} + 1\right) }[/math]
where ERB stands for Equivalent Rectangular Bandwidth.
If we put in 262 Hz (middle C) for [math]\displaystyle{ f }[/math], we get 53 Hz as the width of the bucket centered on middle C. So the upper edge of that bucket is at 262 + 53/2 = 288.5 Hz and the lower edge is at 262 − 53/2 = 235.5 Hz. If we look at the ratio between those, we get 288.5/235.5 = 1.225. That's a 351 ¢ neutral third. If we do the same an octave above middle-C we get 269 ¢. At two octaves up we get 228 ¢. These are fuzzy cutoffs, but it's nice that the numbers agree so well with common practice and experience.
And now, regarding the exact choice of [math]\displaystyle{ \frac{15}{13} }[/math] as the cutoff interval:
If we have a 4:13:15 chord rooted on middle-C. the 13:15 will be centered around 14/4 × 262 Hz = 917 Hz. If we plug that in to the ERB formula and convert the ratio of the bucket edges to cents we get 234 ¢. And 15/13 is about 248 ¢, so that lets us have the chord rooted potentially even a bit lower than middle-C and still not be too dissonant.
If we make a 4:15:17 chord, however, the 15:17 will be centered around 16/4 × 262 Hz. We've already noted that this gives a bucket edge ratio equivalent to 228 ¢. And 17/15 is 217 ¢. So there's not much point worrying about getting their 17th and 15th harmonics coinciding, when their fundamentals are already creating dissonance.
So here, then is what our integer triangle looks like, now with the min size truncation applied (and the axes hidden moving forward):
2/1 3/1 4/1 5/1 6/1 7/1 8/1 9/1 10/1
3/2 4/2 5/2 6/2 7/2 8/2 9/2 10/2
4/3 5/3 6/3 7/3 8/3 9/3 10/3
5/4 6/4 7/4 8/4 9/4 10/4
6/5 7/5 8/5 9/5 10/5
7/6 8/6 9/6 10/6
9/7 10/7
10/8
If we had a much larger truncated integer limit triangle example, we could observe that the min size truncation's boundary line cuts across the diagram as a perfectly straight diagonal out from the origin at the top left.
So now we've lost [math]\displaystyle{ \frac{8}{7} }[/math], [math]\displaystyle{ \frac{9}{8} }[/math], and [math]\displaystyle{ \frac{10}{9} }[/math], all three of which are smaller than [math]\displaystyle{ \frac{15}{13} }[/math].
Max size truncation
In the absence of octave reduction, the intervals in our target-interval set can get quite large. Just take a gander across our top row, where everything is "over 1"; at the rightmost extreme we have 10/1, which is over three octaves above the root. Wide intervals tend to be less sensitive to mistuning, because the relative amplitudes of the coinciding partials tend to be very different, and therefore do not noticeably reinforce or cancel. And so their tuning is taken care of automatically by the tuning of smaller intervals that can be stacked to make them. For example: Provided that [math]\displaystyle{ \frac{5}{4} }[/math] and [math]\displaystyle{ \frac{2}{1} }[/math] are in the target-interval set, we don't need to worry about the tuning of [math]\displaystyle{ \frac{5}{1} }[/math] or [math]\displaystyle{ \frac{10}{1} }[/math]. If we were to include[math]\displaystyle{ \frac{5}{1} }[/math] and [math]\displaystyle{ \frac{10}{1} }[/math] in the target-interval set, they might well take accuracy away from intervals that need it more, like [math]\displaystyle{ \frac{5}{4} }[/math] and [math]\displaystyle{ \frac{2}{1} }[/math].[note 33] The odd limit diamond had solved this problem with octave-reduction. But the truncated integer limit triangle gives no special treatment to the octave in this way, so we need to take special care to eliminate intervals from our integer triangle which are too large to have enough sensitivity to mistuning to be worth inclusion, using up our precious limited damage-reduction resources as discussed in the earlier "importance of exclusivity" section.
In setting a maximum interval size, we are essentially answering the question, "How large does an interval have to get before it is sufficiently insensitive to mistuning?" Any sharp cutoff for this is going to be somewhat arbitrary, but we went with [math]\displaystyle{ \frac{13}{4} }[/math] as the widest interval to include in our default target-interval sets. This is in part from a consideration that 13's presence in both the min and max size bounds, [math]\displaystyle{ \frac{15}{13} }[/math] and [math]\displaystyle{ \frac{13}{4} }[/math], helpfully reduces the memory load, and in part because, according to Wikipedia's list of chords page (linked earlier), the widest commonly named chords are thirteenth chords. In this case, "thirteenth" is referring to a diatonic general interval size category, but it happens to be the case that the harmonic series representative for this size category is the 13th harmonic.[note 34]
So here, then is what our integer triangle looks like, now with both min and max size truncation applied:
2/1 3/1
3/2 4/2 5/2 6/2
4/3 5/3 6/3 7/3 8/3 9/3
5/4 6/4 7/4 8/4 9/4 10/4
6/5 7/5 8/5 9/5 10/5
7/6 8/6 9/6 10/6
9/7 10/7
10/8
Again, if we had a much larger truncated integer limit triangle example, we could observe that the max size truncation's boundary line cuts across the diagram as a perfectly straight diagonal out from the origin at the top left, just the same as the min size truncation's boundary line. It's just that here, while the min's line cuts across the bottom, the max's line cuts across the top.
We've now dropped every "over one" interval past [math]\displaystyle{ \frac{3}{1} }[/math], every "over two" interval past [math]\displaystyle{ \frac{6}{2} }[/math], and every "over three" interval past [math]\displaystyle{ \frac{9}{3} }[/math]; these are all greater than [math]\displaystyle{ \frac{13}{4} }[/math].
Max complexity truncation
The final piece of our truncation process to address is the max complexity truncation. Again, to reduce the cognitive load, we feature the number 13 in this step: simply take the product complexity (that's the numerator times the denominator, e.g. complexity([math]\displaystyle{ \frac{5}{4} }[/math]) = 20), and if that's greater than 13 times the integer limit[note 35], then exclude the interval.
Note that we use plain old product complexity, not the log-product complexity that we use by default for damage weight. There's no reason to complicate complexity with a logarithm here (we are still deferring the reason for doing so to damage weight until a later article), and so this leaves us with the convenience of computing these complexities with mental math, if need be.
For our 10-TILT example, where 10 is the integer limit, that's a max (product) complexity of 130. The interval remaining in our set with the largest product complexity, however, is [math]\displaystyle{ \frac{10}{7} }[/math], which has a complexity of 70, only about halfway to our limit. So in this case, the max complexity truncation has no effect.
Eliminate redundancies
For convenience, let's reproduce the current state of our truncated integer triangle:
2/1 3/1
3/2 4/2 5/2 6/2
4/3 5/3 6/3 7/3 8/3 9/3
5/4 6/4 7/4 8/4 9/4 10/4
6/5 7/5 8/5 9/5 10/5
7/6 8/6 9/6 10/6
9/7 10/7
10/8
Our last step is to reduce intervals to lowest terms and de-dupe.
2/1 3/1
3/2 5/2
4/3 5/3 7/3 8/3
5/4 7/4 9/4
6/5 7/5 8/5 9/5
7/6
9/7 10/7
So this is our final 10-TILT: [math]\displaystyle{ \left\{ \frac{2}{1}, \frac{3}{1}, \frac{3}{2}, \frac{4}{3}, \frac{5}{2}, \frac{5}{3}, \frac{5}{4}, \frac{6}{5}, \frac{7}{3}, \frac{7}{4}, \frac{7}{5}, \frac{7}{6}, \frac{8}{3}, \frac{8}{5}, \frac{9}{4}, \frac{9}{5}, \frac{9}{7}, \frac{10}{7} \right\} }[/math]. That's a total of 18 target-intervals. So we've gone back up to almost the same count of intervals as we had with our odd limit diamond scheme (as it would be used with a 7-(prime-)limit temperament, i.e. we're comparing a 9-OLD to a 10-TILT), but this truncated integer limit triangle scheme is designed to cover a much wider range of tunings so it can be understood to have compacted more power into the same count of intervals.[note 36]
When choosing our max complexity, we used the inclusion of [math]\displaystyle{ \frac{6}{5} }[/math] at the 5-limit a reality check. Nor did we think our scheme should exclude [math]\displaystyle{ \frac{9}{7} }[/math] from the 7-prime-limit or [math]\displaystyle{ \frac{15}{13} }[/math] from the 13-limit, although that one was borderline. New kinds of consonant thirds (and sometimes fourths) are what most musicians are looking for when they go to higher prime limits, because the most consonant chords are made from stacks of thirds (and sometimes fourths). It's debatable whether [math]\displaystyle{ \frac{15}{13} }[/math] counts as a consonant third, because of both its small size and its complexity, but given the right timbre and the right other notes in the chord, it may be relatively consonant, and therefore its precise tuning may matter. We think that George Secor cared about the error in [math]\displaystyle{ \frac{15}{13} }[/math] in designing his 29-HTT, but not anything more complex than that. So that is why this interval serves as both our minimum interval size as well as a final guidepost for the definition of our max complexity.[note 37]
Our scheme's max complexity truncation actually has no effect, then, until past the 13-prime-limit, at the 17-TILT, which is the first max integer which permits an interval above the minimum interval size whose denominator is greater than 13, while the numerator is at the integer limit, thus allowing an interval whose complexity is greater than the integer limit times 13, namely, [math]\displaystyle{ \frac{17}{14} }[/math].
If we had used a much larger truncated integer limit triangle where the max complexity truncation had an effect, we would find that the shape its boundary makes is not a straight line like the integer limit's boundary or the size truncation's boundaries, but actually a smooth curve—specifically a hyperbola—that comes from the extreme top right of the diagram, shooting for the origin but instead of going straight into it, curving away from it and instead shooting toward the bottom left.
Eventually we hit a point, which is the 42-TILT—the default TILT for the 41-prime limit—beyond which the complexity limit of [math]\displaystyle{ 13n }[/math] (in combination with the size limits) overpowers the integer limit [math]\displaystyle{ n }[/math], in the sense that we don't get any ratio of [math]\displaystyle{ 43 }[/math] in the 46-TILT (the default for the 43-prime-limit). We have to go to the 47-TILT before we get [math]\displaystyle{ \frac{43}{14} }[/math]. And the only ratio of [math]\displaystyle{ 41 }[/math] we get in the 42-TILT is [math]\displaystyle{ \frac{41}{13} }[/math]. We don’t think this is unreasonable. George Secor agreed with Erv Wilson that the 41-prime-limit adds nothing new, because ratios of 41 sound too much like ratios of 5. This can be explained by the existence of the 41-limit schismina, [math]\displaystyle{ \frac{6561}{6560} }[/math], 0.26 ¢, [-5 8 -1 0 0 0 0 0 0 0 0 0 -1⟩. In Sagittal notation's systematic comma naming scheme, its name would be the "5.41-schismina"). But these are only our default target-interval sets. You are free to specify a larger-numbered TILT or design your own set.
This all said, between the max and min size truncations and the max complexity truncation, the size truncations are much more important. The complexity truncation plays a role much more similar to the integer limit. When you have max and min size truncations, you might only need either an integer limit or a max product complexity; you might not need both. Because in combination with a min size truncation, an integer limit implies a max product complexity. And in combination with a max size truncation, a max product complexity implies an integer limit. Even when the min size is zero cents, an integer limit implies a max product complexity; no interval more complex than [math]\displaystyle{ \frac{n}{n-1} }[/math] is permitted. So you may well decide you prefer a target-interval set scheme which only uses one or the other of a max complexity or an integer limit.
Comparing the odd limit diamond and truncated integer limit triangle
We began our investigations which led to the development of the truncated integer limit triangle upon noticing shortcomings in the way the odd limit diamond represented harmonic reality.
These shortcomings weren't apparent to us at first, because they only began to affect tuning when we attempted to use the odd limit diamond outside of the context that the Target tunings page of the wiki presents it in. To be specific, on that page, the odd limit diamond is only used with pure-octave tunings that do not weight damage. This pure-octave, unity-weight context renders any factors of 2 in the target-interval set irrelevant to damage:
- With pure octaves, none of these factors of 2 contribute any error.
- Without any damage weight, the difference these factors of 2 would make in complexity functions is also moot.
So what is the consequence? Well, for example, this means that by including [math]\displaystyle{ \frac{3}{2} }[/math] in our target-interval set, we are also in a sense targeting the damage to all other members of the same octave-equivalent interval class, which includes [math]\displaystyle{ \frac{3}{1} }[/math], [math]\displaystyle{ \frac{4}{3} }[/math], [math]\displaystyle{ \frac{8}{3} }[/math], etc.
So we can see, for starters, that in this pure-octave, unity-weight case, it is redundant for the odd limit diamond to include both [math]\displaystyle{ \frac{3}{2} }[/math] and [math]\displaystyle{ \frac{4}{3} }[/math]. But this isn't actually that big of a deal. It's not the real problem we're concerned about. In fact, the truncated integer limit triangle also has this (relatively trivial) problem.[note 38]
The real problem here arises when the odd limit diamond is used outside of its original pure-octave, unity-weight context. To be clear, whenever either of these tuning traits are not true, the factors of 2 in target-intervals affect their damage values; it is only when both of these traits are true that factors of 2 become irrelevant. And so outside that context—whether it's by complexity- or simplicity- weighting our damage, or by tempering our octave—minimizing damage to [math]\displaystyle{ \frac{3}{2} }[/math] and minimizing the damage to [math]\displaystyle{ \frac{4}{3} }[/math] diverge into separate issues (though still interconnected issues, to be sure).
So now it's actually a good thing—outside the pure-octave unity-weight damage context, that is—that the odd limit diamond already at least contains two key intervals from this octave-reduced interval class (as it does for every such interval class that it had representation for).[note 39] But what about the interval [math]\displaystyle{ \frac{3}{1} }[/math]? This interval is not included in the odd limit diamond, but it will have different damage yet from either of those two, and it's also a reasonably-sized and low-complexity interval that we should care about damage to, since it is likely to come up in our music. And by similar logic we may also want to target [math]\displaystyle{ \frac{8}{3} }[/math], and that interval will have different damage still from the other three intervals. And so on. Our definition of damage is capturing how the differing counts of 2's in these intervals are meaningful to us.
The point here is that the odd limit diamond seems to have been designed less as a target-interval set scheme so much as a target octave-reduced interval class set scheme. But this is no good in general, because the fundamental mechanics of tuning optimization—as we've been learning them here—can not understand interval classes; they treat the members of target-interval sets as just that: intervals. And so as soon as we depart from the context of pure octaves and unity-weight damage, conflating these two data types (as the odd limit diamond does) starts to be harmful. A target-interval set scheme which accurately represents harmonic reality in general—i.e. including tempered-octave tunings and/or weighted-damage tunings—should ensure that it directly includes any and all of the intervals that are most likely to occur in the harmonies of the music being tuned for, and whose damage we are likely to care about. We designed our truncated integer limit triangle to fulfill this need.
As a particularly illuminating example, consider how the 9-odd limit diamond includes [math]\displaystyle{ \frac{9}{8} }[/math] and [math]\displaystyle{ \frac{16}{9} }[/math], while the 10-truncated integer limit triangle includes neither of these, instead including [math]\displaystyle{ \frac{9}{4} }[/math]. When octaves are tempered, or we're using complexity functions to help us determine how best to fairly distribute our limited optimization resources among our target-intervals, it's wiser to care about [math]\displaystyle{ \frac{9}{4} }[/math], which is more likely to come up in consonant chords than either [math]\displaystyle{ \frac{9}{8} }[/math] or [math]\displaystyle{ \frac{16}{9} }[/math]; the former is too small of an interval (the truncated integer limit triangle excludes any interval smaller than diatonic thirds), and the latter is too complex. So while the intervals [math]\displaystyle{ \frac{9}{8} }[/math] or [math]\displaystyle{ \frac{16}{9} }[/math] may both be results of octave-reduction, but it's good to remember that many important intervals are larger than an octave. The odd limit diamond fails to realize this, as well as that many intervals smaller than an octave are not as important to tune; its octave-reduction approach is good at finding reasonably-sized intervals given how simple it is, but the truncated integer limit triangle's more direct approach does it better.
Concluding notes
Again, our truncated integer triangle is not a thing we will advocate for communal consistency over. Our main motivation was to find a reasonable target-interval set scheme to implement in our RTT library in Wolfram Language. If we learned anything while settling on it, it's that there are many more questions remaining to be answered about this topic, and many more concerns we can imagine people having that we don't satisfy. So have fun exploring if you like, or just go with our recommendation.
Otonal chord
Another reasonable technique to choose a consonance set would be to choose the largest chord of stacked harmonics you're likely to use in the music, then tune for every interval that comes together to make that chord.
For example, in the 7-limit, you might be likely to use a 4:5:6:7:9 chord. Or maybe you want to focus on the 4:5:6:7 chord. You can just specify a set or range of harmonics, and then just take every interval in that chord. So for the 4:5:6:7 case, we'd have [math]\displaystyle{ \left\{ \frac{5}{4}, \frac{6}{4}, \frac{7}{4}, \frac{6}{5}, \frac{7}{5}, \frac{7}{6} \right\} }[/math] (that [math]\displaystyle{ \frac{6}{4} }[/math] would be reduced to [math]\displaystyle{ \frac{3}{2} }[/math]).
Held-intervals
As you may remember from the initial definitions section of this article, our target intervals are those whose damages we wish to minimize, while our held intervals are those whose damages we hold at zero no matter what. So we have two different sets of intervals here. We care about the tunings of the intervals in both sets, but between the two sets, we care about the held ones even more than the target ones.
The most common choice of interval that people hold unchanged is the octave, [math]\displaystyle{ \frac{2}{1} }[/math], owing to it being the typical interval of equivalence, or equave. For many people, a pitch system with an impure octave is inconceivable to work with.
Set vs. basis
Another important difference between target-intervals and held-intervals is that the target-intervals of a tuning scheme are fully and directly given in the form of a set, while the full set of held-intervals is only represented indirectly in the form of a basis. We call this our held-interval basis, and notate it as [math]\displaystyle{ \mathrm{H} }[/math].
The held-interval set (whenever it exists and is non-empty) always has an infinite count of members. So the held-interval set is not the practical object with which to specify tuning scheme. Instead, we want a finite basis for this infinite-sized set, or in other words, we want a finite representation of the infinite set of intervals, in the form of a finite set of intervals that any member of the infinite set could be built out of.
But why would anyone request an infinite number of intervals to be held unchanged? Well, that's not really how most people would think of it. Most people would explicitly ask only for one interval, such as a held-octave, or for a couple intervals, such as a held-octave plus a held-{5/4} perhaps. So what happens is this: that infinite number of held-intervals arises automatically from the one or few explicitly asked for.
For example, if we hold octaves [math]\displaystyle{ \frac{2}{1} }[/math] unchanged, then certainly double-octaves [math]\displaystyle{ \frac{4}{1} }[/math] will also be unchanged, and triple-octaves and so on. And if we request a held-interval basis of [math]\displaystyle{ \left[\frac{2}{1}, \frac{5}{4}\right] }[/math], then we can see that any combination of any (multiple) of these intervals will also be held unchanged, such as [math]\displaystyle{ \frac{8}{5} }[/math], [math]\displaystyle{ \frac{25}{16} }[/math], etc. etc.
On the other hand, just because we have [math]\displaystyle{ \frac{2}{1} }[/math] and [math]\displaystyle{ \frac{5}{4} }[/math] in our target-interval set, that does not mean that we should consider [math]\displaystyle{ \frac{4}{1} }[/math], [math]\displaystyle{ \frac{8}{5} }[/math], or [math]\displaystyle{ \frac{25}{16} }[/math] also to be in our target-interval set. We may not want to expend the temperament's limited resources on such wide or complex intervals.
So the target-interval set [math]\displaystyle{ \mathrm{T} }[/math] is simple. If an interval is in the set, you see it directly itself in the list; if not, it's out. But we should remember that whenever we request a held-interval in [math]\displaystyle{ \mathrm{H} }[/math], we get infinity more held-intervals for free.
Don't worry if the idea of a basis is not crystal clear yet; we'll look into it in more detail in the next article, in the context of a temperament's set of vanishing commas, which is also represented as a basis (the discussion is here, if you want to skip ahead: Duality, nullspace, commas, bases, canonicalization).
Sizes of target-interval sets and held-interval bases
Typically, people choose a target-interval set which has more intervals than the temperament has generators. Doing so isn't difficult, considering the vast majority of temperaments people use are rank-1 or rank-2, i.e. with only one or two generators. Mathematically we can express this tendency as [math]\displaystyle{ k \gt r }[/math], where [math]\displaystyle{ k }[/math] is the count of target-intervals and [math]\displaystyle{ r }[/math] is the rank of the temperament (which is the same thing as the count of generators). Every target-interval set scheme we've looked at thus far will satisfy this condition; even the smaller only primes set scheme generates target-interval sets where [math]\displaystyle{ k = d }[/math], where [math]\displaystyle{ d }[/math] is the dimensionality of the temperament, satisfies this, because for any non-JI temperament, [math]\displaystyle{ d \gt r }[/math].
When [math]\displaystyle{ k }[/math] is bigger than [math]\displaystyle{ r }[/math] as is typical, there is no way to tune each of the target-intervals purely. This is the essence of tempering.
If for some weird reason we ever tried choosing fewer target-intervals than we had generators—that is, [math]\displaystyle{ k \lt r }[/math]—then we wouldn't even have enough information to finalize our tuning of the temperament. For example, suppose for meantone temperament we chose our target-interval set to be simply [math]\displaystyle{ \left\{ \frac{2}{1} \right\} }[/math]. Okay, well, great. So we set the first generator to exactly [math]\displaystyle{ \frac{2}{1} }[/math], but then what do you want us to do with the other generator? It could be anything. (This situation should basically never come up; we're just including it here for completeness.)
If we choose exactly the same number of target-intervals as we have generators, though, then we find ourselves with the opportunity to tune all of our target-intervals purely. Basically, this is because each of our generators can be assigned the exclusive job of approximating a different one of our target-intervals, whether it does so directly by being that target-interval, or it does so by exactly evenly dividing into it. However, this is still a degenerate target-interval set, but for a different reason. It's because with [math]\displaystyle{ k = r }[/math] like this, it would be better to describe the situation another way: our target-interval set is empty, and instead these intervals are our held intervals. They're a different set of intervals.
We should say that a target-interval set of this small size is not really the best way to tune a temperament for actual musical performance. Typically we see these sorts of tuning schemes used not directly, but only as ways to identify the extreme edge cases of good tuning ranges, such as in the diamond tradeoff tuning range.
So there must be at least as many target-intervals as there are generators, or else we have insufficient instruction to tune our temperament. But when combining target-intervals and held-intervals, this requirement shifts slightly. Now, it is the case that the total count of held-intervals [math]\displaystyle{ h }[/math] and target-intervals [math]\displaystyle{ k }[/math] must be at least the count of generators [math]\displaystyle{ r }[/math]. Mathematically speaking, we say [math]\displaystyle{ h + k \geq r }[/math].
In the absence of target-intervals ([math]\displaystyle{ k=0 }[/math]), we find that the held-interval count [math]\displaystyle{ h }[/math] must be exactly the count of generators, that is, [math]\displaystyle{ h = r }[/math]. And when we have both target-intervals and held-intervals, the more general statement is simply [math]\displaystyle{ h \leq r }[/math]. Again, this is because each held interval requires its own dedicated generator, so you can have up to as many held-intervals as you have generators to allocate to each, but no more.[note 40]
Note that when we speak of the held-interval count, we are speaking of the cardinality of the held-interval basis; as discussed in the previous section, the total count of held-intervals is always [math]\displaystyle{ ∞ }[/math] (whenever it is not 0, anyway). All we're really interested in is the minimum count of held-intervals required to describe the full infinite set of them.
The importance of exclusivity
We've already covered the importance of exclusivity when it comes to the members of our target-interval set. Now we'll take a look at the importance of exclusivity for our held-interval basis.
Each held-interval we request of our tuning scheme further constrains its possibilities for optimization. In the extreme, when we've gotten so picky—hand-picking so many held-intervals that each of our generators is strapped down to nailing a different one of them—then there is no room left for optimization, and the tuning is completely determined by our choice of held-intervals. We get exactly what we've asked for: no more, no less. And so it's only when we've chosen held-intervals that are in the ballpark of an optimized tuning that we'll get a good tuning.
This is all to say that when we seek a tuning for musical performance purposes, one that is optimized to a temperament overall, it's better to entrust things to our preferred optimization procedure; the fewer held-intervals we choose, the less we'll interfere with it.
Unchanged-intervals
The intervals we hold unchanged will always end up in our tuning's unchanged-interval basis. However, they may not always be the only intervals left unchanged under a given tuning of a temperament. For example, we might ask an optimizer for a held-octave tuning of meantone, and get back quarter-comma meantone, which has not only an unchanged [math]\displaystyle{ \frac{2}{1} }[/math], but also an unchanged [math]\displaystyle{ \frac{5}{4} }[/math].
Examples
Let's compare a few example tunings of magic temperament:
- One with only target-intervals,
- One with only held-intervals,
- And one with both.
We'll compare the tunings by damage lists, specifically the damages to the truncated integer limit triangle, which also happens to be the set we'll use for the two tunings here which call for target-intervals (note that while typically we reserve our variable [math]\displaystyle{ \textbf{d} }[/math] for the list of damages to the target-interval list, we're slightly abusing it here, to demonstrate this idea). To isolate the effects of the target and held-intervals, we've gone with the same optimization power—minimax—and damage weight slope—unity-weight—for all three of these tunings, though the actual choice of unity-weight minimax is arbitrary here (as was the choice of magic temperament).
Only target-intervals
So first, we have our tuning with only a target-interval set, the truncated integer limit triangle:
[math]\displaystyle{ 𝒕_ᴛ = \val{1204.936 & 1906.891 & 2791.249} }[/math]
[math]\displaystyle{
\begin{array} {lccccccccccccccc}
& & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\
\textbf{d}_ᴛ & = & [ & 4.936 & 4.936 & 0.000 & 4.936 & 0.000 & 0.000 & 4.936 & 4.936 & ] \\
\end{array}
}[/math]
This happens to lead us to a tuning where all three primes 2, 3, and 5 are tuned wide by the same amount. This way, the errors cancel out when the primes are set on opposite sides of the fraction bar in [math]\displaystyle{ \frac{3}{2} }[/math], [math]\displaystyle{ \frac{5}{2} }[/math], and [math]\displaystyle{ \frac{5}{3} }[/math], causing their damages to all stay zero. Meanwhile, the target-intervals with three total primes—[math]\displaystyle{ \frac{4}{3} }[/math], [math]\displaystyle{ \frac{5}{4} }[/math], and [math]\displaystyle{ \frac{6}{5} }[/math]—end up tying with the damage to the primes.
Only held-intervals
Next, we have our tuning with only an held-interval basis, which we've chosen to be [math]\displaystyle{ \left\{ \frac{2}{1}, \frac{5}{4} \right\} }[/math]. Conveniently both of these intervals are in the truncated integer limit triangle, so we can see both of their zero damage values in the following damage list:
[math]\displaystyle{ 𝒕_ʜ = \val{1200.000 & 1931.569 & 2786.314} }[/math]
[math]\displaystyle{
\begin{array} {lccccccccccccccc}
& & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\
\textbf{d}_ʜ & = & [ & 0.000 & 29.614 & 29.614 & 29.614 & 0.000 & 29.614 & 0.000 & 29.614 & ] \\
\end{array}
}[/math]
We'll also notice that we got zero damage to [math]\displaystyle{ \frac{5}{2} }[/math] as a result. But otherwise, this may not be the best match of temperament and held-interval basis! That's a lot of damage.
Both target-intervals and held-intervals
Finally, we have our tuning using a target-interval set and a held-interval basis. We've chosen our held-interval to be the octave, and the truncated integer limit triangle as our target-interval set.
[math]\displaystyle{ 𝒕_{ᴛʜ} = \val{1200.000 & 1901.955 & 2780.391} }[/math]
[math]\displaystyle{
\begin{array} {lccccccccccccccc}
& & & \frac{2}{1} & \frac{3}{1} & \frac{3}{2} & \frac{4}{3} & \frac{5}{2} & \frac{5}{3} & \frac{5}{4} & \frac{6}{5} \\
\textbf{d}_{ᴛʜ} & = & [ & 0.000 & 0.000 & 0.000 & 0.000 & 5.923 & 5.923 & 5.923 & 5.923 & ] \\
\end{array}
}[/math]
So we can see here how minimizing the damage to the truncated integer limit triangle while requiring the octave stay pure has led to a third completely different tuning. Here, it's best to tune prime 3 also pure, which leads to zero damage to combinations of 2 and 3 such as [math]\displaystyle{ \frac{3}{2} }[/math] and [math]\displaystyle{ \frac{4}{3} }[/math], while all the target-intervals with a single factor of 5 end up with the same damage, apparently whatever damage was dealt to prime 5.
Destretching vs. holding
We can achieve an unchanged-interval one of two ways.
- Destretching: optimize the tuning with respect to the target-interval set, damage, and optimization power as normal, then simply destretch the result until the tempered size of the interval which is desired to be unchanged is the same as its just size.
- Holding: incorporate the fact that certain intervals are to be held unchanged into the optimization procedure. This is also sometimes called constraining.
Holding is hard, but destretching is easy. Let's see how easy destretching is. Suppose the optimization procedure gives you back the tuning map {1201.70 504.13], but you want an unchanged octave. So multiply this map by the ratio between the octave you got and the octave you want, [math]\displaystyle{ \frac{1200}{1201.70} }[/math]. Then you will get:
[math]\displaystyle{
\begin{array} {c}
[ & 1201.70 & × & (\frac{1200}{1201.70}) & & & & & 504.13 & × & (\frac{1200}{1201.70}) & ] & = \\
[ & \cancel{1201.70} & × & (\frac{1200}{\cancel{1201.70}}) & & & & & 504.13 & × & (0.998585) & ] & = \\
[ & & 1200 & & & & & & & 503.42 & & ]
\end{array}
}[/math]
So the pure-octave destretched version of that optimization result is {1200.00 503.42].
So if destretching is so easy, why did we even bring up the holding approach? Well, destretching may be easy, but it's also dumb and limiting. So let's look at the problems of the destretching approach:
- It only works for a single interval (unless another interval we want to be unchanged would also have been unchanged already given the first one being unchanged). As soon as you destretch to accommodate one interval, you mess it up for any others. This is because you're uniformly destretching the entire map. Like we said: it's dumb. So destretching can't even fully address the concept of held-intervals as they've been presented in this article.
- If you only need to destretch your result a tiny bit, no big deal. But the more you need to destretch the result, the less meaningful any of your damage minimization effects will be. So why do all this fancy math to optimize things with respect to all these tuning traits if you're just going to throw all your hard work out the window? It just doesn't make sense.[note 41]
Doing it the held-interval way, you can have as many held-intervals as you like (well, up to the number of generators of your temperament, anyway, as we know by now). The only problem with the held-interval way is that it's harder to figure out how to make it work. Fortunately, explanations are all ready to go in our article on tuning computations.
Note that the destretched-interval and the held-intervals approaches cannot be combined, even if you wanted to; that's because destretching after optimization would compromise the unchangedness of any interval that had been held unchanged during the optimization.
Tuning
Logarithms
Somehow, in this article series about the fundamentals of RTT tuning, we've gotten by without talking about logarithms much (aside from some discussion in the previous article here). And if you're like me, Douglas (at least me a couple years ago before I forced myself to attain a lot of experience with them) you're relieved about that; logarithms are one of those heady mathematical concepts that can be a real pain in the neck for some people, mathematicians or otherwise. So far we've managed only to mention logarithms in the context of complexity functions. We managed to use prime tuning maps and generator tuning maps back in the Damage - example section without bringing them up. Well, they were there the whole time—built into those tuning maps—we just avoided surfacing them at that time.
So now let's take a little time to investigate how RTT uses logarithms. We hope you'll find this explanation of how they work and why we use them accessible, even if logarithms do make your neck hurt.
The cents size formula
If you are familiar with the use of logarithms in xenharmonics at all, it's probably been in the formula for the size of a musical interval in cents, such as:
[math]\displaystyle{
\text{size-in-cents}\left(\frac{3}{2}\right) = 1200×\log_2\left(\frac{3}{2}\right) = 701.955
}[/math]
In other words, to find the cents for an interval, we take its base-2 logarithm, then multiply by 1200. In still other words:
- We find the exponent to which we'd need to raise 2 in order to get our interval, which tells us how many octaves our interval is, because an octave is the interval [math]\displaystyle{ \frac{2}{1} }[/math].
- In this case, the [math]\displaystyle{ \log_2\left(\frac{3}{2}\right) }[/math] is equal to [math]\displaystyle{ 0.585 }[/math], and if you calculate [math]\displaystyle{ 2^{0.585} }[/math], you get [math]\displaystyle{ 1.5 }[/math], which is the same thing as [math]\displaystyle{ \frac{3}{2} }[/math].
- Then we use the [math]\displaystyle{ 1200 }[/math] to convert from octaves to cents, since there are 1200 cents per octave.
The RTT version
In RTT, we do a similar thing, but in a slightly different way. RTT is largely an application of a field of mathematics called linear algebra to xenharmonics. We mentioned linear algebra (LA for short) briefly earlier when explaining the diagonalization of the weight matrix. And if you've gone through our article on mappings, you'll be familiar how we use LA to map prime-count vectors to generator-count vectors. Basically, we take a mapping and an interval, and through the mathemagic of matrix multiplication, get a mapped interval:
[math]\displaystyle{
\begin{align}
\left[ \begin{array} {rrr}
1 & 2 & 3 \\
0 & {-3} & {-5} \\
\end{array} \right]
\left[ \begin{array} {r}
{-1} \\
1 \\
0 \\
\end{array} \right]
&=
\left[ \begin{matrix}
(1×{-1}) + (2×1) + (3×0) \\
(0×{-1}) + ({-3}×1) + ({-5}×0) \\
\end{matrix} \right]
\\[12pt]
&=
\left[ \begin{matrix}
{-1} + 2 + 0 \\
0 + {-3} + 0 \\
\end{matrix} \right]
\\[12pt]
&=
\left[ \begin{array} {r}
1 \\
{-3} \\
\end{array} \right]
\end{align}
}[/math]
So when RTT does this cents calculation, it does it the LA way too: using vectors and matrices:
[math]\displaystyle{
\begin{align}
\text{size-in-cents}\left(\left[ \begin{array} {r} {-1} \\ 1 \\ \end{array} \right]\right)
&=
1200 × \left[ \begin{matrix} \log_2{2} & \log_2{3} \end{matrix} \right] \left[ \begin{array} {r} {-1} \\ 1 \\ \end{array} \right]
\\[12pt]
&=
1200 × (({-1} × \log_2{2}) + (1 × \log_2{3}) )
\\[12pt]
&=
701.955
\end{align}
}[/math]
Something you may notice soon is that we've now represented our interval [math]\displaystyle{ \frac{3}{2} }[/math] not in quotient form anymore, but in vector form, specifically a prime-count vector, in this case [-1 1⟩, meaning it has one prime 2 in its denominator (negative sign) and one prime 3 in its numerator. In other words, we've broken it down and are expressing it in terms of its prime factorization.
Gearing down in complexity
But probably the most critical result to observe here is that we get the same answer doing the calculation this way. We can explain this using a logarithmic identity:
[math]\displaystyle{
\log\left(\frac{n}{d}\right) = \log{n} - \log{d}
}[/math]
Which in this case crops up as:
[math]\displaystyle{
\begin{align}
\log_2\left(\frac{3}{2}\right)
&=
0.585
\\
\log_2{3} - \log_2{2}
&=
1.585 - 1.000 \\
&=
0.585
\end{align}
}[/math]
What this is revealing is how logarithms help us gear down one order of operational complexity, i.e. from multiplication to addition (or in this case specifically, from division to subtraction, though these are essentially the same as multiplication and addition, respectively). As long as we choose a base—in this case we've chosen 2, which is a very reasonable choice in a musical situation, where the interval [math]\displaystyle{ \frac{2}{1} }[/math] is of special psychoacoustic importance as an equave—then anything we might otherwise multiply we can instead express in the form of an exponent of this shared base, and instead add them.
Making linear algebra (LA) work for RTT
"But"—you might protest—"I agree that addition is simpler than multiplication, but surely you can't be serious that it's worth the overhead of this converting into exponents of a shared base shenanigans!"
"I am serious," I would reply. "And don't call me Shirley."
The reason this overhead is worth it is because it's what allows us to make LA work for RTT tuning. Without it, we simply couldn't use LA for this part of our application.
Think about it this way. LA is just a general mathematical tool. It has no idea that it's being used for RTT, and wasn't designed specifically for RTT. The vectors and matrices we use are completely unaware of the fact that the numbers we regular temperament theoreticians put into them represent exponents of prime numbers. Prime factorization has nothing in particular to do with LA.
When we want to take such prime-count vectors and compute their cents value, or get them back into their quotient forms, etc. what we need to do is raise each of our primes to the exponent this vector pairs it with, and then find the product of all of these powers. And unfortunately LA can't help us with that, at least not directly.
LA does handle something very similar to that sort of thing, though, and does it very well. LA has a natural way to multiply (i.e. instead of exponentiate) up two lists of matched-up things, and then find their sum (i.e. instead of product).
Is this ringing any bells? Being unable to find a product—but being able to find a sum!—sounds like a perfect application for a logarithm, something that is designed to help us gear down in operational complexity one step, from multiplication to addition, or in other words from products to sums.
We also note that the relationship between exponentiation and multiplication is the same as that between multiplication and addition, i.e. multiplication is one order of operational complexity lower than exponentiation, and so again logarithms are right tool for the job of gearing down from exponentiation to multiplication.
The dot product
So what is this wonderful feature of LA, you ask? Well, it is known as the dot product.
If you've gotten this far, you probably already know the dot product, even if you don't know it by name. Basically, matrix multiplication is nothing more than a series of dot products—every possible dot product, in fact—between two matrices, and then the arrangement of the results of those dot products into a new matrix. An individual dot product is, as you might expect given how we just pitched it above, a matching up of entries of two vectors with equal counts of entries, then taking each of those matched entries' products, and summing them up.
Let's demonstrate by example how we use logarithms to make LA's dot product work for RTT. Well, first, by counterexample. So suppose we've got this vector:
[math]\displaystyle{
\left[ \begin{array} {r}
{-3} \\
{-1} \\
2 \\
\end{array} \right]
}[/math]
And we know that unless otherwise specified, this vector gives the counts of primes, specifically, the primes, in order, starting from the first prime. So we could represent those as a vector, too:
[math]\displaystyle{
\left[ \begin{matrix}
2 & 3 & 5 \\
\end{matrix} \right]
}[/math]
(This one's written as a row, but that's not particularly important right now.) And by "count" we mean "exponent", so when we zip up these two lists together, we want to get something like this:
[math]\displaystyle{
(2^{-3}) × (3^{-1}) × (5^2)
}[/math]
Which equals [math]\displaystyle{ \frac{5×5}{2×2×2×3} = \frac{25}{24} = 1.041\overline{6} }[/math], the interval that [-3 -1 2⟩ is intended to represent. Good! Except for one problem: we're still doing exponentiation and taking the product, and that's not how the dot product works. If we were to actually put those two vectors together in LA, we wouldn't find the right answer. Instead we'd find:
[math]\displaystyle{
\begin{align}
\left[ \begin{matrix}
2 & 3 & 5 \\
\end{matrix} \right]
\left[ \begin{array} {r}
{-3} \\
{-1} \\
2 \\
\end{array} \right]
&= \\[10pt]
(2×{-3}) + (3×{-1}) + (5×2)
&= \\[10pt]
{-6} + {-3} + 10
&= \\[10pt]
1
\end{align}
}[/math]
So that's not what we want! To make LA work for us, we need to gear down, and we can accomplish that by taking the logarithm of our primes:
[math]\displaystyle{
\log_2{
\left[ \begin{matrix}
2 & 3 & 5 \\
\end{matrix} \right]
}
=
\left[ \begin{matrix}
\log_2{2} & \log_2{3} & \log_2{5} \\
\end{matrix} \right]
}[/math]
Now when we perform the dot product:
[math]\displaystyle{
\begin{align}
\left[ \begin{matrix}
\log_2{2} & \log_2{3} & \log_2{5} \\
\end{matrix} \right]
\left[ \begin{array} {r}
{-3} \\
{-1} \\
2 \\
\end{array} \right]
&= \\[10pt]
(\log_2{2}×{-3}) + (\log_2{3}×{-1}) + (\log_2{5}×2)
&= \\[10pt]
(1×{-3}) + (1.584963×{-1}) + (2.321928×2)
&= \\[10pt]
{-3} + {-1.584963} + 4.643856
&= \\[10pt]
0.058894
\end{align}
}[/math]
and so if we just take that value and reunite it with its base, 2, then we find [math]\displaystyle{ 2^{0.058894} = 1.041\overline{6} = \frac{25}{24} }[/math]. We've done it.
Back to tuning maps
So let's tie this back to the just-prime tuning maps we saw earlier. They are closely related to these log-prime maps. In fact, the only real difference is that they're multiplied by 1200. Check out what happens when we do this:
[math]\displaystyle{
\begin{align}
1200 \left[ \begin{matrix}
\log_2{2} & \log_2{3} & \log_2{5} \\
\end{matrix} \right]
&= \\[10pt]
\left[ \begin{matrix}
1200×1 & 1200×1.585 & 1200×2.322 \\
\end{matrix} \right]
&= \\[10pt]
\left[ \begin{matrix}
1200.000 & 1901.955 & 2786.314 \\
\end{matrix} \right]
\end{align}
}[/math]
That's all there is to it!
Info flow
In the initial definitions section, we briefly discussed the difference between temperament and tuning. In this section we will look at this distinction in more detail, and in particular the relationships between structures that carry temperament and tuning information.
We can begin with a look at a basic problem in RTT: "what is the size in cents of the approximation of a justly intoned musical interval in a given tuning of a given temperament?"
The simplest way
To find this answer, perhaps the most straightforward method is to take the vector representation of the JI interval, [math]\displaystyle{ \textbf{i} }[/math], which is more specifically a prime-count vector, and map it using the tempered-prime tuning map, or "tuning map" for short[note 42], which is notated [math]\displaystyle{ 𝒕 }[/math]. So, our answer is [math]\displaystyle{ 𝒕·\textbf{i} }[/math], which we can also write without the dot product explicitly notated, as [math]\displaystyle{ 𝒕\textbf{i} }[/math].
For example, in quarter-comma meantone, we can find the size of our ~[math]\displaystyle{ \frac{6}{5} }[/math] by mapping [1 1 -1⟩ against the tuning map ⟨1200 1896.578 2786.312], to get [math]\displaystyle{ (1200×1) + (1896.578×1) + (2786.312×{-1}) = 310.266 }[/math].
But there are other ways of processing this situation. Some ways are more convenient than others, depending on your goals.
The other simplest way
Another way to look at this problem which certainly rivals if not exceeds the [math]\displaystyle{ 𝒕\textbf{i} }[/math] way in popularity is to use a generator tuning map instead, notated [math]\displaystyle{ 𝒈 }[/math]. Using this way, the entries of the tuning map represent the tunings of the temperament's generators, rather than the approximations of the prime harmonic basis as we see in the prime tuning map. But that means that our interval vector's entries must also be in terms of the temperament's generators, again, not in terms of the prime harmonics; this mapped interval would be notated [math]\displaystyle{ M\textbf{i} }[/math].
This way is nice because there are fewer generators than there are prime harmonics, so it requires fewer total numbers. Repeating the same example, ~[math]\displaystyle{ \frac{6}{5} }[/math] is represented by the generator-count vector [2 -3} in meantone, and the quarter-comma meantone generator tuning map is {1200 696.578], so we get [math]\displaystyle{ (1200 × 2) + (696.578 × {-3}) = 310.266 }[/math], the same answer as before.
The essential difference with this way is that the temperament information has been transferred from the tuning map into the interval. This is easy to see when we recognize that the tuning map [math]\displaystyle{ 𝒕 }[/math] is equivalent to the generator tuning map [math]\displaystyle{ 𝒈 }[/math] combined with the temperament mapping matrix [math]\displaystyle{ M }[/math]. Then we can see that our first method was really:
[math]\displaystyle{
(𝒈M)\textbf{i}
}[/math]
And our second method was really:
[math]\displaystyle{
𝒈(M\textbf{i})
}[/math]
Either way, we wind up with [math]\displaystyle{ 𝒈M\textbf{i} }[/math] in the end.
Info kinds
So let's reflect on the kind of information each of these structures carries. The simplest way to put it may be:
- The temperament mapping matrix [math]\displaystyle{ M }[/math] carries the temperament information.
- The generator tuning map [math]\displaystyle{ 𝒈 }[/math] carries the tuning information.
- The tempered-prime tuning map [math]\displaystyle{ 𝒕 }[/math], being the combination of [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ M }[/math], carries both.
Tuning ranges
Sometimes what we're looking for is not a single optimum tuning, but rather a range of good tuning possibilities. For this, we refer you to the article Tuning ranges of regular temperaments.
Systematic tuning scheme names
Moving forward in this article series, in order to expedite and clarify our explanations, we'd like to get you on board with our systematic way of naming tuning schemes.
Optimization
Here's the basic setup:
| Damage weight | Optimization power | Systematic name |
|---|---|---|
| <none> | ∞ | minimax-U |
| complexity | minimax-C | |
| 1/complexity | minimax-S | |
| 1 | 2 | miniRMS-U |
| complexity | miniRMS-C | |
| 1/complexity | miniRMS-S | |
| <none> | 1 | miniaverage-U |
| complexity | miniaverage-C | |
| 1/complexity | miniaverage-S |
We hope that this table appears somewhat self-explanatory, but we will give a brief explanation nonetheless. The core of each name comes from the optimization power:
- When [math]\displaystyle{ ∞ }[/math], the tuning scheme is named "minimax".
- When [math]\displaystyle{ 2 }[/math], it is named "miniRMS".
- When [math]\displaystyle{ 1 }[/math], it is named "miniaverage".
Damage
The part of the name after the hyphen describes what sort of damage is minimized according to that optimization power. Damage weight slope can be indicated by a single letter. When the tuning scheme uses:
- Unity-weight damage, put a U.
- Complexity-weight damage, put a C.
- Simplicity-weight damage, put an S.
So based on the fundamentals we've covered so far, there are only nine basic types of tuning scheme.
We've stated above that we consider log-product complexity to be a good default complexity function in the application of RTT tuning. If for some reason you wish to use a different complexity function, however, such as [math]\displaystyle{ \text{sopfr} }[/math] (sum of prime factors with repetition), the place to fit that in our naming scheme is between the optimization and the damage weight slope, like this: "minimax-sopfr-C".
Target-intervals
Each of these nine basic types of tuning scheme can be used with any target-interval set. That's why we didn't include them in the table above, but it's important to specify them, too.
To specify a target-interval set, simply prefix the tuning scheme with it. For example, "TILT minimax-U" would specify the default truncated integer limit triangle per your temperament's prime limit as the target-interval set.
If your target-interval set is not defined by a commonly used set of rules (a target-interval set scheme), but is just a set of your favorite intervals, you could name it e.g. "{3/2, 5/3, 7/4} miniaverage-S".
A tuning scheme must have a target-interval set. If no target-interval set is specified, though, then the assumption must be that all intervals are target-intervals. This is how we name all-interval tuning schemes. So "minimax-S" is the tuning which minimizes simplicity-weight damage to all intervals.
Held-intervals
To specify a held-interval basis, put it up front, prefixed by "held-", as in "held-octave TILT miniRMS-C" or "held-{2/1, 5/4} minimax-U", etc.
Unlike the target-interval set, a held-interval basis is not required. So if no held-intervals are specified, our naming system assumes there is none.
We note that the historical tuning scheme named with the single word "minimax"—while it does use unity-weight damage—is not exactly the same as the tuning named "minimax-U" by our system. This is because it makes two assumptions: one about its target-interval set, and one about its held-interval basis (whereas our naming scheme accounts for a wide variety of minimax tuning schemes). The odd limit diamond (OLD) is its target-interval set, and the octave is its single held-interval. So in our naming system, this scheme should be called "held-octave OLD minimax-U".
(Similarly, "destretched-octave" etc. may be used, if you're into that sort of thing.)
How to read
It may help to think of reading "5-OLD minimax-U" as "the tuning causing to members of the 5-odd-limit diamond the minimized maximum unweighted damage."
Defaults
Note that, so far, the only defaults we have in our system are the assumption of "all-intervals" (the universal set) when no target-interval set is given, and no held-intervals (the empty set) when no held-interval basis is given. But we do not have a default optimization power or damage weight slope. We think it is best to include these pieces of information in any tuning scheme's name.
See also
Thank you so much for making it with us this far. If you're interested in continuing your journey along the Dave Keenan & Douglas Blumeyer's guide to RTT tuning series:
- 4. Exploring temperaments to understand how different temperaments intersect with each other
- 5. Units analysis: to look at temperament and tuning in a new way, think about the units of the values in frequently used matrices
- 6. Tuning computation: for methods and derivations; learn how to compute tunings, and why the methods work
- 7. All-interval tuning schemes: the variety of tuning scheme that is most commonly named and written about on the Xenharmonic wiki
- 8. Alternative complexities: for tuning optimizations with error weighted by something other than log-product complexity
- 9. Tuning in nonstandard domains: for temperaments of domains other than prime limits, and in particular nonprime domains
Footnotes and references
- ↑ Throughout this article, we'll be using three decimal places of precision for tuning cents. We note that as long as you don't stack more than 20 generators, a [math]\displaystyle{ \small{0.005} \, \mathsf{¢} }[/math] error in the generator will never cause a beat cycle time of less than 4 seconds between 4 kHz harmonics. And so for all but the most complex temperaments, 2 decimal places of precision should be sufficient. And this was the level of accuracy used in Paul Erlich's paper A Middle Path. But we've gone with 3 decimal places to be safe.
- ↑ he calls this the "TOP" tuning scheme, standing for "Tempered Octaves Please", as well as for "Tenney OPtimal". More on this scheme another time, though.
- ↑ To untie it a bit instead, we could mention that some people think of rank-1 temperaments (equal temperaments), or rather EDOs (equal divisions of the octave) as tunings of higher-rank temperaments. This is an informal way of thinking about things. By this, these people simply mean that all generator sizes of the higher rank temperament are chosen to be multiples of a single generator size, which equally divides an octave (which may or may not be one of the generators). This typically assumes pure octaves because otherwise it wouldn't specify the exact size of the generators. For many, the convenience of working with an EDO is not worth sacrificing, and so choosing a tuning becomes a problem of choosing the ET that causes the least damage, rather than using the general methods we discuss in this article series.
- ↑ Cents are the most commonly used logarithmic pitch unit, though octaves are also popular, and any logarithmic pitch unit can be used to quantify damage if one really wants to.
- ↑ We recognize that the term "damage" was popularized by Paul Erlich in his Middle Path paper, where it has a more specific meaning, namely, log-product-simplicity-weighted absolute error. However, since then, the term has come to be used more generally, with the expectation that a tuning scheme or complexity- or simplicity-weighting is prefixed to specify it. So, in accord with this community trend, we are using "damage" in a generalized way here, to refer to any quantity whose purpose is to model the reduction in some kind of valued audible quality of an otherwise just (pure) target-interval, due to retuning it. It's hard to think of a better term for a reduction in a valued quality than "damage".
- ↑ For a rare example of a sort of tuning scheme designed otherwise, see proportional beats tuning schemes, as discussed here: linear chord. However proportional beating schemes can be seen as minimizing (down to zero) an unusual kind of damage, and as having an unusual kind of target that is not an interval. The damage is computed as a meta-error, and the target is a meta-ratio, a ratio between the frequency deltas of two interval ratios. When the meta-ratio is 1:1, the damage is the difference between the absolute errors in two intervals when those errors have units of Hz, not cents. This is generalized in the obvious way to meta-ratio other than 1:1. But meta-ratios with integers greater than 3 are too complex to be audible. This can also be generalized to extended meta-ratios with more than 2 components, but the rank of the temperament must be greater than or equal to the number of components in the meta-ratio or it won't be able to zero the damage (i.e. equalize (or proportionalize) the beats).
- ↑ The "miniaverage" statistic is more often referred to as "least absolute values" or "least absolutes"; reflected in that name is the fact that the taking of the absolute values is treated as part of computing that statistic. And this is often an assumed step in the minimax statistic as well. Or the inputs are expected to be non-negative (see https://mathworld.wolfram.com/PowerMean.html). In the case of least squares, this issue is moot because squaring values automatically makes them positive, and that is true of any even power. In our regular temperament tuning context, the absolute values have already been taken in computing the damages, and power means alone do not include the taking of absolute values, so we have chosen in this text to define these statistics as not including the taking of absolute values.
- ↑ We move the "T" for "truncated" after the 6 to obtain a pronounceable acronym.
- ↑ We're glossing over some details about limits here. This will be explained further in the "non-unique tunings" section.
- ↑ We came across a fascinating result while researching this part of this article. Apparently, there is a relationship between the [math]\displaystyle{ ∞ }[/math]th root and the natural logarithm function [math]\displaystyle{ \ln }[/math], and an analogous relationship between the [math]\displaystyle{ ∞ }[/math]th power and the natural exponential function [math]\displaystyle{ \exp }[/math]. If we take the formula
[math]\displaystyle{ \log_e{x} = \lim_{m \to 0} \frac{x^m - 1}{m} }[/math]
and we substitute [math]\displaystyle{ \frac{1}{p} }[/math] for [math]\displaystyle{ m }[/math], we get
[math]\displaystyle{ \log_e{x} = \lim_{p \to ∞} (\sqrt[p]{x} - 1) × p }[/math]
and the inverse of that is
[math]\displaystyle{ e^x = \lim_{p \to ∞} (\frac{x}{p} + 1)^p }[/math]
So [math]\displaystyle{ \ln{x} }[/math] could be described as "the infinite root of x, minus one, times infinity", and [math]\displaystyle{ \exp{x} }[/math] could be described as "x over infinity, plus 1, to the infinite power". In a way, it's the limit of the relationship between multiplication and exponentiation. Cool! - ↑ Or should we say the "[math]\displaystyle{ 1 }[/math]-mean reader"?
- ↑ Many of the most popular complexity functions used for this purpose are frequently referred to (e.g. on the wiki) as "heights". We find this terminology confusing and in conflict with the existing meaning of "pitch height", and have thus avoided it entirely (see Height#History for details). Even the Wikipedia article for this mathematical notion of height says that it "quantifies complexity"
- ↑ We are referring specifically to the complexity function used by the tuning scheme that has historically been called "TE"; as Graham Breed (the creator of this scheme) says, "...10:9 being simpler than 9:8 means TE complexity of a ratio doesn't quite work either. When scoring tunings, you average (implicitly) over a lot of different ratios so this comes out in the wash" (see: https://www.facebook.com/groups/xenharmonicmath/posts/2161713553968855/?comment_id=2161715193968691&reply_comment_id=2166167390190138), though we admit that we're not quite certain what Graham means here by "comes out in the wash".
- ↑ We also entertained referring to these as "progressive' and "regressive" weighting, with "unity-weight" being "flat" (yes, so it was a reference to taxation schemes), until we realized that "flat" already has a musical meaning and that this could be confusing. Also, due to the presence of "Euclidean" in names for types of tuning schemes we haven't mentioned in this series yet, and "flat" being a synonym for "Euclidean" in some physics contexts, that was problematic too.
- ↑ We also briefly entertained pursuing a "weighting" vs. "buoyancy" dichotomy, inspired by the use in Graham Breed's writings, but we ultimately found that attempting to leverage this pun was more confusing than helpful. Dave had a serious attempt at finding a word for the reciprocal of a weight that did not make the pun that buoyancy makes, considering things like triviality, negligibility, denigration, derogation, deprecation, depreciation, and alleviation. He decided that they all have the problem that a <whatever> of 1/2 doesn't sound like a weight of 2; it just sounds like a weight of 1/2. So we decided to avoid any such term, just relying on the unambiguous noun phrase "reciprocal of the weight" when necessary. Dave consulted with a statistics guru friend on this, and he concurred with the decision, confirming that there is no standard term for this.
- ↑ In that spirit, we noticed a way to generalize damage weight slope as a power which could be placed on a continuum too, like the optimization power is: damage_weight = complexity ^ damage_weight_slope, where the slope as we've discussed it thus far is an exponent equal to −1 (S), 0 (U), or +1 (C). Do enjoy yourself if you want to explore that realm of possibilities, but we do not feel the need to explore it here.
- ↑ So there is a theoretical alternative justification for simplicity-weighting, independent of individually directly audible properties: that it is an attempt to reflect the actual relative occurrence counts of these intervals in musical performance. If this is the thinking, then it may be worth investigating simplicity functions specifically designed to capture this information. For example, Dave has found that the percentage of prime factors [math]\displaystyle{ p }[/math] in the first [math]\displaystyle{ n }[/math] integers can be approximated by: [math]\displaystyle{ \frac{n-1}{\left(p-1\right)n\left(\ln\left(\ln\left(n\right)\right) + 1.0345061758\right)} }[/math]
- ↑ https://publish.uwo.ca/~emacphe3/pipes/acoustics/chanterdata.html shows that the high A on a bagpipe chanter is usually tuned 10 to 30 cents lower than a pure octave above the low A, despite them both playing against a drone that is an octave below the low A. This is thought to be to reduce the size of the melodic step from the high G ([math]\displaystyle{ \frac{7}{4} }[/math]) to the high A.
- ↑ Page 126. And later on page 185 Partch writes: "It is only necessary to remember the decreasing power and increasing subtlety of resolutions to the less familiar identities—7, 9, and 11—if there is any intention of preserving their quality as identities. It is frequently stated that the higher the numbers of a ratio the less obligatory is it that the ratio be given correctly, the more susceptible is the ratio to temperament, and the more willing the ear to compensate for the inaccuracy, and this is of course the justification for the egregious corruption of 5/4 and 6/4 and their complements in Equal Temperament. This is a half-truth, one that is incapable of any verbal characterization that does not employ the word negative or the conception of negativism; it illustrates a type of thinking that is perhaps the most basic of all our intonational limitations. The higher the numbers of a ratio the more subtle its effect, and the more scrupulously should we try to forestall its dissipation in the stronger ratios surrounding it."
- ↑ The use of uppercase letters for these weighted-unit annotations was inspired in part by the annotations used for weighted decibels. Unweighted decibels are written "dB". Decibels with various weightings are written "dB(A)", "dB(C)", "dB(Z)". See https://www.engineeringtoolbox.com/decibel-d_59.html or https://en.wikipedia.org/wiki/A-weighting for more information.
- ↑ They could in theory be zero, but usually any interval whose weight is zero would not appear in a target-interval list to have its damage minimized.
- ↑ The letter 'd' is also used for temperament dimensionality. But in context usually any damage value will be part of a list, in which case the subscript will set it apart. Also it will be upright, whereas dimensionality is italic. So we have [math]\displaystyle{ \mathrm{d}_k }[/math] versus [math]\displaystyle{ d }[/math].
- ↑ Historically "mistuning" has been used as a synonym for the more commonly-used term "error", e.g. in the work of Paul Erlich and Graham Breed. But we need a term for the change in tuning that belongs to the temperament as a whole, which has units of cents per count of each prime, as distinct from the error in specific target-intervals which simply has units of cents. We could have chosen to specialize the term "mistuning" for this purpose, but we prefer to use "retuning" instead.
The origin of this preference was when Bill Wesley critiqued the use of "mistuning" in an early version of our article series, because it imbued the act of tempering with negative connotations. Indeed, the meaning of the prefix "mis-" in the term "mistuning" suggests that the just tuning is correct and the tempered tuning we change it to is somehow wrong. Of course, in RTT we recognize that the tempered tuning is not wrong, rather, it is a different sort of correct; we don't strictly sacrifice quality by changing the tuning of the primes, but also achieve new types of harmonic effects that we couldn't in JI (essentially tempered chords, etc.). Even the other alternative "detuning" has a prefix "de-" which suggests we've undone some tuning— that the just tuning is in tune, and the tempered tuning is out of tune. So, we feel that "retuning" best captures our intentionality with respect to that.
While we must admit that "retuning" contains the meaning of "was in tune, drifted out of tune, and now we're retuning it back to its in-tune state", which is a meaning we don't desire, and a meaning which neither "mistune" nor "detune" are clouded with, it otherwise can just as well mean the thing that we do need to mean, i.e. to go from one tuning to another, or said another way, to represent a delta between tunings.
One might protest, though: why worry about extricating value-judgment from the verb "mistune" when the noun "error" is strongly value-judgmental? It doesn't get much more negative than "error". Well, this difference helps reinforce the concept that retuning is an action done to the temperament as a whole, while error is specific to the target-intervals. When we look at the intentionality of the action—changing the tunings of the primes (or more generally, the basis elements)—this involves a mix of quality sacrifice and of goal achievement, so it's not fair to give the name either an only-positive or only-negative connotation. But when we focus only on considering the effect on the target-intervals, then it's certainly fair to say that things worked out strictly badly for them, at least considered individually out of any harmonic context. So that's error. - ↑ Actually there is a symbol that lets you do that sort of multiplication, and it’s ⨀, but we ultimately decided (it was a tough call though) that it was overall better to stick with matrix multiplication when possible.
- ↑ The "6-truncated integer limit triangle" also works.
- ↑ One might object that since the 6-TILT was tuned to itself here, no other tuning—with respect to only the primes, or otherwise—could have beaten it at its own game, and that in order for us to thoroughly prove that the 6-TILT tuning is generally preferable to the primes-only tuning for typical musical purposes, we should compare their performances across a wider selection of similar such targeted interval sets. That may be so, if the principle this example nonetheless demonstrates is unconvincing to you, and you therefore seek exhaustive empirical evidence instead. We don't personally feel compelled to go to such tedious lengths here, though we'd be happy for interested readers with sufficient time on hand to look into that. For purposes of this article here, we're satisfied enough to have leveraged this single comparison between a primes-only target-interval set tuning and a carefully-chosen target-interval set tuning in order to illustrate the first one of the three shortcomings of primes-only tunings that we listed at the beginning of this section, namely, the one about the naïvety of the primes-only tuning with respect to errors canceling or compounding across the fraction bar.
- ↑ Some of these all-interval schemes which "seemingly" target only the primes are, in fact, equivalent to schemes which target only the primes. But these actual-only-prime-targeting schemes are of no interest in their own right.
- ↑ These sets were also described by Erv Wilson, who called them "reciprocal cross-sets". They could also be thought of as the Cartesian product of a set of odd numbers with a set of those odds' reciprocals, where the resulting ordered pairs are multiplied together.
- ↑ There is an argument that including duplicates of certain ratios in the target list would be a way to place additional emphasis on them. This only makes sense when the optimization power is less than [math]\displaystyle{ ∞ }[/math], though, because a minimax tuning where only the maximum damage matters can't be affected by duplicate target-intervals. This may especially make sense when using a complexity-weight damage, because in such a case you are using the damage weight to express how much precision matters for each interval, and its inclusion count in the target-interval set is how you express how much you care about the given interval. One way to determine which intervals to duplicate would be to simply not eliminate duplicates from the diamond after reducing intervals, as this seems to give a somewhat natural degree of duplication of these intervals, such as you might expect to find in the music itself. We've decided not to complicate matters in the main body of the text with this consideration, but it's just another of the endless examples of ways one might come up with to complicate the process of tuning and procrastinate on actually making some regularly tempered music!
- ↑ It may be worth noting that while the default odd limit diamond for the 5-limit, the 5-OLD, includes the interval [math]\displaystyle{ \frac{8}{5} }[/math], the default truncated integer limit triangle for the 5-limit does not, because this is the 6-TILT which excludes ratios with integers greater than 6, so the 8 in [math]\displaystyle{ \frac{8}{5} }[/math] rules it out. At first we thought this might be a bad thing. But several sources we found cast doubt on whether the minor sixth is a diatonic consonance. And we wonder if we and possibly others may only be used to getting [math]\displaystyle{ \frac{8}{5} }[/math] for free along with [math]\displaystyle{ \frac{5}{4} }[/math] when we assume pure octave tuning.
- ↑ Remember: these cutoffs apply to untempered intervals. It is irrelevant whether an interval, once tempered, might fall within or without this range.
- ↑ https://en.wikipedia.org/wiki/Just-noticeable_difference#Music_production_applications
- ↑ We thank Paul Erlich and Flora Canou for prompting us to rewrite this paragraph, by correcting our earlier erroneous claim that such wide intervals were of little harmonic importance and not commonly used.
- ↑ It's a fascinating quirk that from "seventh" to "fourteenth", the corresponding harmonic falls into the diatonic size category (assuming the 4th harmonic is the root), with the 7th harmonic being 969 ¢, on the smaller side of a diatonic seventh, the 8th harmonic being 1200 ¢, of course a diatonic eighth (compound unison), the 9th harmonic being 1404 ¢ which is a diatonic ninth (compound second), etc. all the way up to the 14th harmonic being 2169 ¢, on the smaller side of a diatonic fourteenth (compound seventh). So this is all the compound diatonic steps, plus the seventh just before them.
- ↑ Our maximum complexity is a function of the integer limit, not the prime limit. This is because prime limit is an implementation detail of RTT—in particular how it manifests the fundamental theorem of arithmetic through linear algebra, expressing prime factorizations as vectors. Whether harmonic complexity increases even more with the addition of a prime than it increases with the addition of a composite odd or even integer is not important in this context; all that is important is that harmonic complexity increases at all with the addition of each higher integer, and so this is why we base our max complexity on the integer limit. We note, however, that the max complexity will be indirectly a function of the prime limit via the integer limit in the case that one relies upon the default integer limit for their truncated integer limit triangle, which as discussed earlier, is a function of the temperament's prime limit.
- ↑ The intersection with the temperament's interval subspace (usually a prime limit) must also be taken, which should almost go without saying, since any other intervals are outside the temperament. This should be true of any interval set scheme—TILT, OLD, or otherwise.
This issue will never matter if the default max integer is chosen, i.e. the integer one less than the next prime limit, which prevents any integers with primes beyond the temperament's prime limit appearing in the target-interval set. However, it is not unreasonable at the 5-prime-limit to wish to tune with respect to intervals with, say, 9's in them, or perhaps even 15's. So some people may like to use a 10-, 12-, or 16- TILT to tune a 5-limit temperament with, and in this case, they will need to cut out intervals with 7's, 11's, or 13's in their factorizations. This is done simply by enforcing the prime limit of the temperament as part of the target-interval set scheme.
Unlike the other limits we've looked at—integer, size, and complexity—the prime limit does not make a neat line through the array of ratios—straight, curved, or otherwise. Instead, it chaotically slices rows and columns out of the results. Were we to use our 10-TILT at the 5-limit, we'd end up with:2/1 3/1 3/2 5/2 4/3 5/3 8/3 5/4 9/4 6/5 8/5 9/5
The entire row for 7 and column for 7 have been deleted.
- ↑ Dave did have a moment of doubt about the factor of 13 in our max complexity, because some people consider the true just minor triad to be 16:19:24 rather than the inverse of the major triad 4:5:6, or in other words 1/(4:5:6) = 10:12:15. The 16:19:24 chord is very close to the minor triad of 12-EDO. To include this chord within our maximum complexity would require increasing the factor of 13 to a 14, which would result in a maximum complexity of 22×14=308 at the 19-prime-limit of that chord, thereby allowing the 19/16 interval from that chord (complexity 304), though not the 24/19 interval from that chord (complexity 456), though that's above 22-integer-limit, so no matter. We decided that the memorability of all the 13's in our various bounds was worth preserving, though, and wondered whether the one time Dave thought he heard specialness in 16:19:24 while using a sawtooth wave timbre may only have been the result of a combination-tone effect, or, if it was actually coinciding harmonics, what timbre other than an artificial one like a sawtooth would have sufficient 19th harmonic to make it audible.
- ↑ Including both of these members of the same octave-reduced interval class—[math]\displaystyle{ \frac{3}{2} }[/math] and [math]\displaystyle{ \frac{4}{3} }[/math]—in the same target-interval set for a pure-octave, unity-weight damage tuning scheme means that it will take us longer to do the calculations for that set, but these calculations will ultimately lead to the same tunings.
For small interval sets, though—like we have at the 5-prime-limit—this isn't a big deal to a computer doing the job; the difference between three target-intervals and six is a matter of milliseconds worth of compute time.
So rather than bother complicating the situation by describing a different target-interval set scheme for the special case of pure-octave + unity-weight damage tuning schemes, we suggest that we all just eat the (very low) costs of these extra calculations. - ↑ This may not always be a good thing, though. Consider the case of [math]\displaystyle{ \frac{5}{4} }[/math] and [math]\displaystyle{ \frac{8}{5} }[/math]. The default truncated integer limit triangle for the 5-prime-limit actually excludes [math]\displaystyle{ \frac{8}{5} }[/math] per its integer limit of 6, which is its way of deeming that interval insufficiently worthy of targeting; better, that is, to allocate precious resources to optimizing the tuning of other intervals with lower integers.
- ↑ You may be wondering what happens if an interval that is in the held-interval basis [math]\displaystyle{ \mathrm{H} }[/math] is also in the target-interval set [math]\displaystyle{ \mathrm{T} }[/math], or if any held-interval for that matter—i.e. any interval that is a linear combination of those in the held-interval basis—is in the target-interval set. The answer is: it doesn't really matter. You will find the same exact tuning. So, for example, you can use an off-the-shelf target-interval set such as a TILT, along with a held-octave, without having to worry about the fact that [math]\displaystyle{ \frac{2}{1} }[/math] is also in the target-interval set.
- ↑ Re: the relative value of destretching and holding. We grabbed a set of eleven reasonably prominent 5-limit temperaments: meantone, blackwood, dicot, augmented, mavila, porcupine, srutal, hanson, magic, negri, and tetracot, finding a total of 1743.235 ¢(U|C|S) damage for the destretched-octave tunings and 1712.369 ¢(U|C|S) damage for the destretched-octave tunings. That's only a 30.866 total weighted cents worth of damage difference. But then you'd want to divide that by the count of target-intervals (6 in the 5-odd-limit diamond, appropriate since these are all pure-octave tunings), the count of tunings (9, being the 3×3 matrix of standard optimization powers and damage weight slopes), and the count of temperaments (11), so that's actually only an average of 30.866 ¢(U, C, S) / (6 × 9 × 11 = 594) = 0.052 ¢(U, C, S) damage spared to each target by choosing a held-interval tuning rather than a destretched-interval tuning. So in the aggregate it doesn't matter.
But we did find specific examples where held-interval tunings significantly outperform destretched-interval tunings. We checked to see if for any of those temperament tunings there was a difference of greater than 5 ¢(?) between the two tunings. For only 2 of the 9 × 11 = 99 temperament tunings checked, there was. In both cases, the better tuning was the held-interval one.
The first noteworthy example were the pair of odd-diamond minimax-C tunings of dicot, [⟨1 1 2] ⟨0 2 1]⟩. The (tempered-octave) odd-diamond minimax-C tuning is ⟨1192.342 1889.818 2733.422], so the destretched-octave version is 1200/1192.342 times that, which is ⟨1200.000 1901.955 2750.978], so we also get an unchanged prime 3 but a prime 5 which is narrow by 35.336 ¢, and in a complexity-weight tuning, that means that the most complex interval in the set, 8/5, with a complexity of log₂(8 × 5) = 5.322, and which also happens to isolate that 5, not canceling out any of its error (well, nor is it contributing any extra error on the other side of the fraction bar), is going to amplify that damage tremendously, so we have 35.336 ¢ × 5.322 (C) = 188.054 ¢(C) as our max damaged target. And the held-octave tuning fares a bit better, managing to find ⟨1200.000 1904.823 2752.411], which only does 180.428 ¢(C) damage to 8/5, and in this case, it ties that damage with 6/5, by putting a little of it onto prime 3.
The second noteworthy example were the pair of odd-diamond miniaverage-C tunings of mavila, [⟨1 0 7] ⟨0 1 -3]⟩. The (tempered-octave) odd-diamond minimax-C tuning is ⟨1191.543 1863.178 2751.264], so the held-octave version is 1200/1191.543 times that, which is ⟨1200.000 1875.461 2773.618]. In the tempered-octave tuning, the damage to 5/3 is basically zero, because both prime 3 and prime 5 are tuned quite narrow, but proportionally so. And the held-octave tuning shares this feature, so the damage to 5/3 is also basically zero. The difference between these two tunings is which other target's error gets sent to zero; for the tempered-octave tuning, it's 8/5, since it has control over prime 2's, while for the held-octave tuning it's 6/5. What's weird about the destretched tuning is that even though the proportion between prime 3 and prime 5 is the same in cents, of course, it is different in terms of how much they contribute to complexity. It missed the memo that it was important to preserve that relationship. So we end up with the destretched tuning doing 50 to 100 ¢(C) damage to each interval, and thereby causing over 7 extra weighted cents worth of damage across the board. - ↑ Both "tempered" as opposed to "just" and "primes" as opposed to "generators" may be assumed if not specified otherwise.