Generator embedding optimization
When optimizing tunings of regular temperaments, it is fairly quick and easy to find approximate solutions, using (for example) the general method which is discussed in D&D's guide to RTT and available in D&D's RTT library in Wolfram Language. This RTT library also includes four other methods which quickly and easily find exact solutions. These four methods are further different from the general method insofar as they are not general; each one works only for certain optimization problems. It is these four specialized exact-solution methods which are the subject of this article.
Two of these four specialized methods were briefly discussed in D&D's guide, along with the general method, because these specialized methods are actually even quicker and easier than the general method. These two are the only held-intervals method, and the pseudoinverse method. But there's still plenty more insight to be had into how and why exactly these methods work, in particular for the pseudoinverse method, so we'll be doing a much deeper dive into it in this article here than was done in D&D's guide.
The other two of these four specialized methods—the zero-damage method, and the coinciding-damage method—are significantly more challenging to understand than the general method. Most students of RTT would not gain enough musical insight by familiarizing themselves with them to have justified the investment. This is why these two methods were not discussed in D&D's guide. However, if you feel compelled to understand the nuts and bolts of these methods anyway, then those sections of the article may well appeal to you.
This article is titled "Generator embedding optimization" because of a key feature these four specialized methods share: they can all give their solutions as generator embeddings, i.e. lists of prime-count vectors, one for each generator, where typically these prime-count vectors have non-integer entries (and are thus not JI). This is different from the general method, which can only give generator tuning maps, i.e. sizes in cents for each generator. As we'll see, a tuning optimization method's ability to give solutions as generator embeddings is equivalent to its ability to give solutions that are exact.
Intro
A summary of the methods
The three biggest sections of this article are dedicated to three specialized tuning methods, one for each of the three special optimization powers: the pseudoinverse method is used for [math]\displaystyle{ p = 2 }[/math] (miniRMS tuning schemes), the zero-damage method is used for [math]\displaystyle{ p = 1 }[/math] (miniaverage tuning schemes), and the coinciding-damage method is used for [math]\displaystyle{ p = ∞ }[/math] (minimax tuning schemes).
These three methods also work for all-interval tuning schemes, which by definition are all minimax tuning schemes (optimization power [math]\displaystyle{ ∞ }[/math]), differing instead by the power of the power norm used for the interval complexity by which they simplicity-weight damage. But it's not the interval complexity norm power [math]\displaystyle{ q }[/math] which directly determines the method used, but rather its dual power, [math]\displaystyle{ \text{dual}(q) }[/math]: the power of the dual norm minimized on the retuning magnitude. So the pseudoinverse method is used for [math]\displaystyle{ \text{dual}(q) = 2 }[/math], the zero-damage method is used for [math]\displaystyle{ \text{dual}(q) = 1 }[/math], and the coinciding-damage method is used for [math]\displaystyle{ \text{dual}(q) = ∞ }[/math].
If for some reason you've decided that you want to use a different optimization power than those three, then no exact solution in the form of a generator embedding is available, and you'll need to fall back to the general tuning computation method, linked above.
The general method also works for those special powers [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], and [math]\displaystyle{ ∞ }[/math], however, so if you're in a hurry, you should skip this article and lean on that method instead (though you should be aware that the general method offers less insight about each of those tuning schemes than their specialized methods do).
Exact vs. approximate solutions
Tuning computation methods can be classified by whether they give an approximate or exact solution.
The general method is an approximate type; it finds the generator tuning map [math]\displaystyle{ 𝒈 }[/math] directly, using trial-and-error methods such as gradient descent or differential evolution whose details we won't go into. The accuracy of approximate types depends on how long you are willing to wait.
In contrast, the exact type work by solving for a matrix [math]\displaystyle{ G }[/math], the generator embedding.
We can calculate [math]\displaystyle{ 𝒈 }[/math] from this [math]\displaystyle{ G }[/math] via [math]\displaystyle{ 𝒋G }[/math], that is, the generator tuning map is obtained as the product of the just tuning map and the generator embedding.
Because [math]\displaystyle{ 𝒈 = 𝒋G }[/math], if [math]\displaystyle{ 𝒈 }[/math] is the primary target, not [math]\displaystyle{ G }[/math], and a formula for [math]\displaystyle{ G }[/math] is known, then it is possible to substitute that into [math]\displaystyle{ 𝒈 = 𝒋G }[/math] and thereby bypass explicitly solving for [math]\displaystyle{ G }[/math]. For example, this was essentially what was done in the Only-held intervals method and Pseudoinverse method sections of D&D's guide: Tuning computation).
Note that with any exact type that solves for [math]\displaystyle{ G }[/math], since it is possible to have an exact [math]\displaystyle{ 𝒋 }[/math], it is also possible to find an exact [math]\displaystyle{ 𝒈 }[/math]. For example, the approximate value of the 5-limit [math]\displaystyle{ 𝒋 }[/math] we're quite familiar with is ⟨1200.000 1901.955 2786.314], but its exact value is ⟨[math]\displaystyle{ 1200×\log_2(2) }[/math] [math]\displaystyle{ 1200×\log_2(3) }[/math] [math]\displaystyle{ 1200×\log_2(5) }[/math]], so if the exact tuning of quarter-comma meantone is [math]\displaystyle{ G }[/math] = {[1 0 0⟩ [0 0 ¼⟩], then this can be expressed as an exact generator tuning map [math]\displaystyle{ 𝒈 }[/math] = {[math]\displaystyle{ (1200×\log_2(2))(1) + (1200×\log_2(3))(0) + (1200×\log_2(5))(0) }[/math] [math]\displaystyle{ (1200×\log_2(2))(0) + (1200×\log_2(3))(0) + (1200×\log_2(5))(\frac14) }[/math]] = {[math]\displaystyle{ 1200 }[/math] [math]\displaystyle{ \dfrac{1200×\log_2(5)}{4} }[/math]].
Also note that any method which solves for [math]\displaystyle{ G }[/math] can also produce [math]\displaystyle{ 𝒈 }[/math] via this [math]\displaystyle{ 𝒋G }[/math] formula. But methods which solve directly for [math]\displaystyle{ 𝒈 }[/math] cannot provide a [math]\displaystyle{ G }[/math], even if a [math]\displaystyle{ G }[/math] could have been computed for the given type of optimization problem (such as a minimax type, which notably is the majority of tuning optimizations used on the wiki). In a way, tuning maps are like a lossily compressed form of information from embeddings.
Here's a breakdown of which computation methods solve directly for [math]\displaystyle{ 𝒈 }[/math], and which can solve for [math]\displaystyle{ G }[/math] instead:
| Optimization power | Method | Solution type | Solves for |
|---|---|---|---|
| [math]\displaystyle{ 2 }[/math] | Pseudoinverse | Exact | [math]\displaystyle{ G }[/math] |
| [math]\displaystyle{ 1 }[/math] | Zero-damage | Exact | [math]\displaystyle{ G }[/math] |
| [math]\displaystyle{ ∞ }[/math] | Coinciding-damage | Exact | [math]\displaystyle{ G }[/math] |
| General | Power | Approximate | [math]\displaystyle{ 𝒈 }[/math] |
| power limit | |||
| N/A | Only held-intervals | Exact | [math]\displaystyle{ G }[/math] |
The generator embedding
Roughly speaking, if [math]\displaystyle{ M }[/math] is the matrix which isolates the temperament information, and [math]\displaystyle{ 𝒋 }[/math] is the matrix which isolates the sizing information, then [math]\displaystyle{ G }[/math] is the matrix that isolates the tuning information. This is a matrix whose columns are prime-count vectors representing the generators of the temperament. For example, a Pythagorean tuning of meantone temperament would look like this:
[math]\displaystyle{
G =
\left[ \begin{array} {rrr}
1 & {-1} \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
}[/math]
The first column is the vector [1 0 0⟩ representing [math]\displaystyle{ \frac21 }[/math], and the second column is the vector [-1 1 0⟩ representing [math]\displaystyle{ \frac32 }[/math]. So generator embeddings will always have the shape [math]\displaystyle{ (d, r) }[/math]: one row for each prime harmonic in the domain basis (the dimensionality), one column for each generator (the rank).
Pythagorean tuning is not a common tuning of meantone, however, and is an extreme enough tuning of that temperament that it should be considered unreasonable. We gave it as our first example anyway, though, in order to more gently introduce the concept of generator embeddings, because its prime-count vector columns are simple and familiar, while in reality, most generator embeddings consist of prime-count vectors which do not have integer entries. Therefore, these prime-count vectors do not represent JI intervals, and are unlike any prime-count vectors we've worked with so far. For another example of a meantone tuning, then, one which is more common and reasonable, let's consider the quarter-comma tuning of meantone. Its generator embedding looks like this:
[math]\displaystyle{
G =
\left[ \begin{array} {rrr}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
}[/math]
Algebraic setup
The basic algebraic setup of tuning optimization looks like this:
[math]\displaystyle{
\textbf{d} = |\,𝒈M\mathrm{T}W - 𝒋\mathrm{T}W\,|
}[/math]
When we break [math]\displaystyle{ 𝒈 }[/math] down into [math]\displaystyle{ 𝒋 }[/math] and a [math]\displaystyle{ G }[/math] we're solving for, the algebraic setup of tuning optimization comes out like this:
[math]\displaystyle{
\textbf{d} = |\,𝒋GM\mathrm{T}W - 𝒋G_{\text{j}}M_{\text{j}}\mathrm{T}W\,|
}[/math]
We can factor things in both directions this time (and we'll take [math]\displaystyle{ 𝒋 }[/math] outside the absolute value bars since it's guaranteed to have no negative entries):
[math]\displaystyle{
\textbf{d} = 𝒋\,|\,(GM - G_{\text{j}}M_{\text{j}})\mathrm{T}W\,|
}[/math]
But wait—there are actually two more matrices we haven't recognized yet, on the just side of things. These are [math]\displaystyle{ G_{\text{j}} }[/math] and [math]\displaystyle{ M_{\text{j}} }[/math]. Unsurprisingly, these two are closely related to [math]\displaystyle{ G }[/math] and [math]\displaystyle{ M }[/math], respectively. The subscript [math]\displaystyle{ \text{j} }[/math] stands for "just intonation", so this is intended to indicate that these are the generators and mapping for JI.
We could replace either or both of these matrices with [math]\displaystyle{ I }[/math], an identity matrix. On account of both [math]\displaystyle{ G_{\text{j}} }[/math] and [math]\displaystyle{ M_{\text{j}} }[/math] being identity matrices, we can eliminate them from our expression
[math]\displaystyle{
\textbf{d} = 𝒋\,|\,(GM - II)\mathrm{T}W\,|
}[/math]
Which reduces to:
[math]\displaystyle{
\textbf{d} = 𝒋\,|\,(P - I)\mathrm{T}W\,|
}[/math]
Where [math]\displaystyle{ P }[/math] is the projection matrix found as [math]\displaystyle{ P = GM }[/math].
So why do we have [math]\displaystyle{ G_{\text{j}} }[/math] and [math]\displaystyle{ M_{\text{j}} }[/math] there at all? For maximal parallelism between the tempered side and the just side. In part this is a pragmatic decision, because as we work with these sorts of expressions moving forward, we'll prefer something rather than nothing in this position anyway. But there's also a pedagogical goal here, which is to convey how in JI, the mapping matrix and the generator embedding really are identity matrices, and it can be helpful to stay mindful of it.
You can imagine reading a [math]\displaystyle{ (3, 3) }[/math]-shaped identity matrix like a mapping matrix: how many generators does it take to approximate prime 2? One of the first generator, and nothing else. How many to approximate prime 3? One of the second generator, and nothing else. How many to approximate prime 5? One of the third generator, and nothing else. So this mapping is not much of a mapping at all. It shows us only that in this temperament, the first generator may as well be a perfect approximation of prime 2, the second generator may as well be a perfect approximation of prime 3, and the third generator may as well be a perfect approximation of prime 5. Any temperament which has as many generators as it has primes may as well be JI like this.
And then the fact that the generator embedding on the just side is also an identity matrix finishes the point. The vector for the first generator is [1 0 0⟩, a representation of the interval [math]\displaystyle{ \frac21 }[/math]; the vector for the second generator is [0 1 0⟩, a representation of the interval [math]\displaystyle{ \frac31 }[/math]; and the vector for the third generator is [0 0 1⟩, a representation of the interval [math]\displaystyle{ \frac51 }[/math].
We can even understand this in terms of a units analysis, where if [math]\displaystyle{ M_{\text{j}} }[/math] is taken to have units of g/p, and [math]\displaystyle{ G_{\text{j}} }[/math] is taken to have units of p/g, then together we find their units to be ... nothing. And an identity matrix that isn't even understood to have units is definitely useless and to be eliminated. Though it's actually not as simple as the [math]\displaystyle{ \small \sf p }[/math]'s and [math]\displaystyle{ \small \sf g }[/math]'s canceling out; for more details, see here.
So when the interval vectors constituting the target-interval list [math]\displaystyle{ \mathrm{T} }[/math] are multiplied by [math]\displaystyle{ G_{\text{j}}M_{\text{j}} }[/math] they are unchanged, which means that multiplying the result by [math]\displaystyle{ 𝒋 }[/math] simply computes their just sizes.
Deduplication
Between target-interval set and held-interval basis
Generally speaking, held-intervals should be removed if they also appear in the target-interval set. If these intervals are not removed, the correct tuning can still be computed; however, during optimization, effort will have been wasted on minimizing damage to these intervals, because their damage would have been held to 0 by other means anyway.
Of course, there is some cost to the deduplication itself, but In general, it should be more computationally efficient to remove these intervals from the target-interval set in advance, rather than submit them to the optimization procedures as-is.
Duplication of intervals between these two sets will most likely occur when using a target-interval set scheme (such as a TILT or OLD) that automatically chooses the target-interval set.
Constant damage target-intervals
There is also a possibility, when holding intervals, that some target-intervals' damages will be constant everywhere within the tuning damage space to be searched, and thus these target-intervals will have no effect on the tuning. Their preservation in the target-interval set will only serve to slow down computation.
For example, in pajara temperament, with mapping [⟨2 3 5 6] ⟨0 1 -2 -2]}, if the octave is held unchanged, then there is no sense keeping [math]\displaystyle{ \frac75 }[/math] in the target-interval set. The octave [1 0 0 0⟩ maps to [2 0} in this temperament, and [math]\displaystyle{ \frac75 }[/math] [0 0 -1 1⟩ maps to [1 0}. So if the first generator is fixed in order to hold the octave unchanged, then ~[math]\displaystyle{ \frac75 }[/math]'s tuning will also be fixed.
Within target-interval set
We also note a potential for duplication within the target-interval set, irrespective of held-intervals: depending on the temperament, some target-intervals may map to the same tempered interval. For another pajara example, using the TILT as a target-interval set scheme, the target-interval set will contain [math]\displaystyle{ \frac{10}{7} }[/math] and [math]\displaystyle{ \frac75 }[/math], but pajara maps both of those intervals to [1 0}, and thus the damage to these two intervals will always be the same.
However, critically, this is only truly redundant information in the case of a minimax tuning scheme, where the optimization power [math]\displaystyle{ p = ∞ }[/math]. In this case, if the damage to [math]\displaystyle{ \frac75 }[/math] is the max, then it's irrelevant whether the damage to [math]\displaystyle{ \frac{10}{7} }[/math] is also the max. But in the case of any other optimization power, both the presence of [math]\displaystyle{ \frac75 }[/math] and of [math]\displaystyle{ \frac{10}{7} }[/math] in the target-interval set will have some effect; for example, with [math]\displaystyle{ p = 1 }[/math], miniaverage tuning schemes, this means that whatever the identical damage to this one mapped target-interval [1 0} may be, since two different of our target-intervals map to it, we care about its damage twice as much, and thus it essentially gets counted twice in our average damage computation.
Should redundant mapped target-intervals be removed when computing minimax tuning schemes? It's a reasonable consideration. The RTT Library in Wolfram Language does not do this. In general, this may add more complexity to the code than the benefit is worth; it requieres minding the difference between the requested target-interval set count [math]\displaystyle{ k }[/math] and the count of deduped mapped target-intervals, which would require a new variable.
Only held-intervals method
The only held-intervals method was mostly covered here: Dave Keenan & Douglas Blumeyer's guide to RTT/Tuning computation#Only held-intervals method. But there are a couple adjustments we'll make to how we talk about it here.
Unchanged-interval basis
In the D&D's guide article, this method was discussed in terms of held-intervals, which are a trait of a tuning scheme, or in other words, a request that a person makes of a tuning optimization procedure which that procedure will then satisfy. But there's something interesting that happens once we request enough many intervals to be held unchanged—that is, when our held-interval count [math]\displaystyle{ h }[/math] reaches the size of our generator count, also known as rank [math]\displaystyle{ r }[/math]—then we have no room left for optimization. At this point, the tuning is entirely determined by the held-intervals. And thus we get another, perhaps better, way to look at the interval basis: no longer in terms of a request on a tuning scheme, but as a characteristic of a specific tuning itself. Under this conceptualization, what we have is not a helf-interval basis [math]\displaystyle{ \mathrm{H} }[/math], but an unchanged-interval basis [math]\displaystyle{ \mathrm{U} }[/math].
Because in the majority of cases within this article it will be more appropriate to conceive of this basis as a characteristic of a fully-determined tuning, as opposed to a request of tuning scheme, we will be henceforth be dealing with this method in terms of [math]\displaystyle{ \mathrm{U} }[/math], not [math]\displaystyle{ \mathrm{H} }[/math]
Generator embedding
So, substituting [math]\displaystyle{ \mathrm{U} }[/math] in for [math]\displaystyle{ \mathrm{H} }[/math] in the formula we learned from the D&D's guide article:
[math]\displaystyle{
𝒈 = 𝒋\mathrm{U}(M\mathrm{U})^{-1}
}[/math]
This tells us that if we know the unchanged-interval basis for a tuning, i.e. every unchanged-interval in the form of a prime-count vector, then we can get our generators. But the next difference we want to look at here is this: the formula has bypassed the computation of [math]\displaystyle{ G }[/math]! We can expand [math]\displaystyle{ 𝒈 }[/math] to [math]\displaystyle{ 𝒋G }[/math]:
[math]\displaystyle{
𝒋G = 𝒋\mathrm{U}(M\mathrm{U})^{-1}
}[/math]
And cancel out:
[math]\displaystyle{
\cancel{𝒋}G = \cancel{𝒋}\mathrm{U}(M\mathrm{U})^{-1}
}[/math]
To find:
[math]\displaystyle{
G = \mathrm{U}(M\mathrm{U})^{-1}
}[/math]
Pseudoinverse method
Similarly, we can take the pseudoinverse formula as presented in Dave Keenan & Douglas Blumeyer's guide to RTT/Tuning computation#Pseudoinverse method, substitute [math]\displaystyle{ 𝒋G }[/math] for [math]\displaystyle{ 𝒈 }[/math], and cancel out:
[math]\displaystyle{
\begin{align}
𝒈 &= 𝒋\mathrm{T}W(M\mathrm{T}W)^{+} \\
𝒋G &= 𝒋\mathrm{T}W(M\mathrm{T}W)^{+} \\
\cancel{𝒋}G &= \cancel{𝒋}\mathrm{T}W(M\mathrm{T}W)^{+} \\
G &= \mathrm{T}W(M\mathrm{T}W)^{+} \\
\end{align}
}[/math]
Connection with the only held-intervals method
Note the similarity between the pseudoinverse formula [math]\displaystyle{ A^{+} = A^\mathsf{T}(AA^\mathsf{T})^{-1} }[/math] and the only held-interval interval [math]\displaystyle{ G = 𝒋\mathrm{U}(M\mathrm{U})^{-1} }[/math]; in fact, it's the same formula, if we simply substitute in [math]\displaystyle{ M^\mathsf{T} }[/math] for [math]\displaystyle{ \mathrm{U} }[/math].
What this tells us is that for any tuning of a temperament where [math]\displaystyle{ G = M^{+} }[/math], the held-intervals are given by the transpose of the mapping, [math]\displaystyle{ M^\mathsf{T} }[/math]. (Historically this tuning scheme has been called "Frobenius", but we would call it "minimax-E-copfr-S".)
For example, in the [math]\displaystyle{ G = M^{+} }[/math] tuning of meantone temperament ⟨1202.607 696.741], with mapping [math]\displaystyle{ M }[/math] equal to:
[math]\displaystyle{
\left[ \begin{array} {r}
1 & 1 & 0 \\
0 & 1 & 4 \\
\end{array} \right]
}[/math]
The held-intervals are [math]\displaystyle{ M^\mathsf{T} }[/math]:
[math]\displaystyle{
\left[ \begin{array} {r}
1 & 0 \\
1 & 1 \\
0 & 4 \\
\end{array} \right]
}[/math]
or in other words, the two held-intervals are [1 1 0⟩ and [0 1 4⟩, which as ratios are [math]\displaystyle{ \frac61 }[/math] and [math]\displaystyle{ \frac{1875}{1} }[/math], respectively. Those may seem like some pretty strange intervals to be unchanged, for sure, but there is a way to think about it that makes it seem less strange. This tells us that whatever the error is on [math]\displaystyle{ \frac21 }[/math], it is the negation of the error on [math]\displaystyle{ \frac31 }[/math], because when those intervals are combined, we get a pure [math]\displaystyle{ \frac61 }[/math]. This also tells us that whatever the error is on [math]\displaystyle{ \frac31 }[/math], that it in turn is the negation of the error on [math]\displaystyle{ \frac{625}{1} = \frac{5^4}{1} }[/math].[note 1] Also, remember that these intervals form a basis for the held-intervals; any interval that is a linear combination of them is also unchanged.
As another example, the unchanged-interval of the primes miniRMS-U tuning of 12-ET would be [12 19 28⟩. Don't mistake that for the 12-ET map ⟨12 19 28]; that's the prime-count vector you get from transposing it! That interval, while rational and thus theoretically JI, could not be heard directly by humans, considering that [math]\displaystyle{ 2^{12}3^{19}5^{28} }[/math] is over 107 octaves above unison and would typically call for scientific notation to express; it's 128553.929 ¢, which is exactly 1289 ([math]\displaystyle{ = 12^2+19^2+28^2 }[/math]) iterations of the 99.732 ¢ generator for this tuning.
Example
Let's refer back to the example given in Dave Keenan & Douglas Blumeyer's guide to RTT/Tuning computation#Plugging back in, picking up from this point:
[math]\displaystyle{
\scriptsize
𝒈 =
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
\mathrm{T}C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1.000 & \;\;\;0.000 & {-2.585} & 7.170 & {-3.322} & 0.000 & {-8.644} & 4.907 \\
0.000 & 1.585 & 2.585 & {-3.585} & 0.000 & {-3.907} & 0.000 & 4.907 \\
0.000 & 0.000 & 0.000 & 0.000 & 3.322 & 3.907 & 4.322 & {-4.907} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
(M\mathrm{T}C)^\mathsf{T} \\
\left[ \begin{array} {rrr}
1.000 & 0.000 \\ \hline
3.170 & {-4.755} \\ \hline
2.585 & {-7.755} \\ \hline
0.000 & 10.755 \\ \hline
6.644 & {-16.610} \\ \hline
3.907 & {-7.814} \\ \hline
4.322 & {-21.610} \\ \hline
0.000 & 9.814 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
(M\mathrm{T}C(M\mathrm{T}C)^\mathsf{T})^{-1} \\
\left[ \begin{array} {rrr}
0.0336 & 0.00824 \\
0.00824 & 0.00293 \\
\end{array} \right]
\end{array}
}[/math]
In the original article, we simply multiplied through the entire right half of this expression. But what if we stopped before multiplying in the [math]\displaystyle{ 𝒋 }[/math] part, instead?
[math]\displaystyle{
𝒈 =
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
\mathrm{T}C(M\mathrm{T}C)^\mathsf{T}(M\mathrm{T}C(M\mathrm{T}C)^\mathsf{T})^{-1} \\
\left[ \begin{array} {rrr}
1.003 & 0.599 \\
{-0.016} & 0.007 \\
0.010 & {-0.204} \\
\end{array} \right]
\end{array}
}[/math]
The matrices with shapes [math]\displaystyle{ (3, 8)(8, 2)(2, 2) }[/math] led us to a [math]\displaystyle{ (3, \cancel{8})(\cancel{8}, \cancel{2})(\cancel{2}, 2) = (3, 2) }[/math]-shaped matrix, and that's just what we want in a [math]\displaystyle{ G }[/math] here. Specifically, we want a [math]\displaystyle{ (d, r) }[/math]-shaped matrix, one that will convert [math]\displaystyle{ (r, 1) }[/math]-shaped generator-count vectors—those that are results of mapping [math]\displaystyle{ (d, 1) }[/math]-shaped prime-count vectors by the temperament mapping matrix—back into [math]\displaystyle{ (d, 1) }[/math]-shaped prime-count vectors, but now representing the intervals as they sound under this tuning of this temperament.
And so we've found what we were looking for, [math]\displaystyle{ G = \mathrm{T}C(M\mathrm{T}C)^\mathsf{T}(M\mathrm{T}C(M\mathrm{T}C)^\mathsf{T})^{-1} }[/math].
At first glance, this might seem surprising or crazy, that we find ourselves looking at musical intervals described by raising prime harmonics to powers that are precise fractions. But they do, in fact, work out to reasonable interval sizes. Let's check by actually working these generators out through their decimal powers.
This generator embedding [math]\displaystyle{ G }[/math] is telling us that the tuning of our first generator may be represented by the prime-count vector [1.003 -0.016 0.010⟩, or in other words, it's the interval [math]\displaystyle{ 2^{1.003}3^{-0.016}5^{0.010} }[/math], which is equal to [math]\displaystyle{ 2.00018 }[/math], or 1200.159 ¢. As for the second generator, then, we find that [math]\displaystyle{ 2^{0.599}3^{0.007}5^{-0.205} = 1.0985 }[/math], or 162.664 ¢. By checking the porcupine article we can see that these are both reasonable generator sizes.
What we've just worked out with this sanity check is our generator tuning map, [math]\displaystyle{ 𝒈 }[/math]. In general we can find these by left-multiplying the generators [math]\displaystyle{ G }[/math] by [math]\displaystyle{ 𝒋 }[/math]:
[math]\displaystyle{
\begin{array} {ccc}
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
G \\
\left[ \begin{array} {rrr}
1.003 & 0.599 \\
{-0.016} & 0.007 \\
0.010 & {-0.204} \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
\mathbf{g} \\
\left[ \begin{array} {rrr}
1200.159 & 162.664 \\
\end{array} \right]
\end{array}
\end{array}
}[/math]
Pseudoinverse: The "how"
Here we will investigate how, mechanically speaking, the pseudoinverse almost magically takes us straight to that answer we want.
Like an inverse
As you might suppose—given a name like pseudoinverse—this thing is like a normal matrix inverse, but not exactly. True inverses are only defined for square matrices, so the pseudoinverse is essentially a way to make something similar available for non-square i.e. rectangular matrices. This is useful for RTT because the [math]\displaystyle{ M\mathrm{T}W }[/math] matrices we use it on are usually rectangular; they are always [math]\displaystyle{ (r, k) }[/math]-shaped matrices.
But why would we want to take the inverse of [math]\displaystyle{ M\mathrm{T}W }[/math] in the first place, though? To understand this, it will help to first simplify the problem.
- Our first simplification will be to use unity-weight damage, meaning that the weight on each of the target-intervals is the same, and may as well be 1. This makes our weight matrix [math]\displaystyle{ W }[/math] a matrix of all zeros with 1's running down the main diagonal, or in other words, it makes [math]\displaystyle{ W = I }[/math]. So we can eliminate it.
- Our second simplification is to consider the case where the target-interval set [math]\displaystyle{ \mathrm{T} }[/math] is the primes. This makes [math]\displaystyle{ \mathrm{T} }[/math] also equal to [math]\displaystyle{ I }[/math], so we can eliminate it as well.
At this point we're left with simply [math]\displaystyle{ M }[/math]. And this is still a rectangular matrix; it's [math]\displaystyle{ (r, d) }[/math]-shaped. So if we want to invert it, we'll only be able to pseudoinvert it. But we're still in the dark about why we would ever want to invert it.
To finally get to understanding why, let's look to an expression discussed here: Basic algebraic setup:
[math]\displaystyle{
GM \approx G_{\text{j}}M_{\text{j}}
}[/math]
This expression captures the idea that a tuning based on [math]\displaystyle{ G }[/math] of a temperament [math]\displaystyle{ M }[/math] (the left side of this) is intended to approximate just intonation, where both [math]\displaystyle{ G_{\text{j}} = I }[/math] and [math]\displaystyle{ M_{\text{j}} = I }[/math] (the right side of this).
So given some mapping [math]\displaystyle{ M }[/math], which [math]\displaystyle{ G }[/math] makes that happen? Well, based on the above, it should be the inverse of [math]\displaystyle{ M }[/math]! That's because anything times its own inverse equals an identity, i.e. [math]\displaystyle{ M^{-1}M = I }[/math].
Definition of inverse
Multiplying by something to give an identity is, in fact, the very definition of "inverse". To illustrate, here's an example of a true inverse, in the case of [math]\displaystyle{ (2, 2) }[/math]-shaped matrices:
[math]\displaystyle{
\begin{array} {c}
A^{-1} \\
\left[ \begin{array} {rrr}
1 & \frac23 \\
0 & {-\frac13} \\
\end{array} \right]
\end{array}
\begin{array} {c}
A \\
\left[ \begin{array} {rrr}
1 & 2 \\
0 & {-3} \\
\end{array} \right]
\end{array}
\begin{array} {c} \\ = \end{array}
\begin{array} {c}
I \\
\left[ \begin{array} {rrr}
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
}[/math]
So the point is, if we could plug [math]\displaystyle{ M^{-1} }[/math] in for [math]\displaystyle{ G }[/math] here, we'd get a reasonable approximation of just intonation, i.e. an identity matrix [math]\displaystyle{ I }[/math].
But the problem is, as we know already, that [math]\displaystyle{ M^{-1} }[/math] doesn't exist, because [math]\displaystyle{ M }[/math] is a rectangular matrix. That's why we use its pseudoinverse [math]\displaystyle{ M^{+} }[/math] instead. Or to be absolutely clear, we choose our generator embedding [math]\displaystyle{ G }[/math] to be [math]\displaystyle{ M^{+} }[/math].
Sometimes an inverse
Now to be completely accurate, when we multiply a rectangular matrix by its pseudoinverse, we can also get an identity matrix, but only if we do it a certain way. (And this fact that we can get an identity matrix at all is a critical example of the way how the pseudoinverse provides inverse-like powers for rectangular matrices.) But there are still a few key differences between this situation and the situation of a square matrix and its true inverse:
- The first big difference is that in the case of square matrices, as we saw a moment ago, all the matrices have the same shape. However, for a non-square (rectangular) matrix with shape [math]\displaystyle{ (m, n) }[/math], it will have a pseudoinverse with shape [math]\displaystyle{ (n, m) }[/math]. This difference perhaps could have gone without saying.
- The second big difference is that in the case of square matrices, the multiplication order is irrelevant: you can either left-multiply the original matrix by its inverse or right-multiply it, and either way, you'll get the same identity matrix. But there's no way you could get the same identity matrix in the case of a rectangular matrix and its pseudoinverse; an [math]\displaystyle{ (m, n) }[/math]-shaped matrix times an [math]\displaystyle{ (n, m) }[/math]-shaped matrix gives an [math]\displaystyle{ (m, m) }[/math]-shaped matrix, while an [math]\displaystyle{ (n, m) }[/math]-shaped matrix times an [math]\displaystyle{ (m, n) }[/math]-shaped matrix gives an [math]\displaystyle{ (n, n) }[/math]-shaped matrix (the inner height and width always have to match, and the resulting matrix always has shape matching the outer width and height). So: either way we will get a square matrix, but one way we get an [math]\displaystyle{ (m, m) }[/math] shape, and the other way we get an [math]\displaystyle{ (n, n) }[/math] shape.
- The third big difference—and this is probably the most important one, but we had to build up to it by looking at the other two big differences first—is that only one of those two possible results of multiplying a rectangular matrix by its pseudoinverse will actually even give an identity matrix! It will be the one of the two that gives the smaller square matrix.
Example of when the pseudoinverse behaves like a true inverse
Here's an example with meantone temperament as [math]\displaystyle{ M }[/math]. Its pseudoinverse [math]\displaystyle{ M^{+} = M^\mathsf{T}(MM^\mathsf{T})^{-1} }[/math] is {[17 16 -4⟩ [16 17 4⟩]/33. First, we'll look at the multiplication order that gives an identity matrix, when the [math]\displaystyle{ (2, 3) }[/math]-shaped rectangular matrix right-multiplied by its [math]\displaystyle{ (3, 2) }[/math]-shaped rectangular pseudoinverse gives a [math]\displaystyle{ (2, 2) }[/math]-shaped square identity matrix:
[math]\displaystyle{
\begin{array} {c}
M \\
\left[ \begin{array} {r}
1 & 0 & {-4} \\
0 & 1 & 4 \\
\end{array} \right]
\end{array}
\begin{array} {c}
M^{+} \\
\left[ \begin{array} {c}
\frac{17}{33} & \frac{16}{33} \\
\frac{16}{33} & \frac{17}{33} \\
{-\frac{4}{33}} & \frac{4}{33} \\
\end{array} \right]
\end{array}
\begin{array} {c} \\ = \end{array}
\begin{array} {c}
I \\
\left[ \begin{array} {rrr}
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
}[/math]
Let's give an RTT way to interpret this first result. Basically it tells us that [math]\displaystyle{ M^{+} }[/math] might be a reasonable generator embedding [math]\displaystyle{ G }[/math] for this temperament. First of all, let's note that [math]\displaystyle{ M }[/math] was not specifically designed to handle non-JI intervals like those represented by the prime-count vector columns of [math]\displaystyle{ M^{+} }[/math], like we are making it do here. But we can get away with it anyway. And in this case, [math]\displaystyle{ M }[/math] maps the first column of [math]\displaystyle{ M^{+} }[/math] to the generator-count vector [1 0}, and its second column to the generator-count vector [0 1}; we can find these two vectors as the columns of the identity matrix [math]\displaystyle{ I }[/math].
Now, one fact we can take from this is that the first column of [math]\displaystyle{ M^{+} }[/math]—the non-JI vector [[math]\displaystyle{ \frac{17}{33} }[/math] [math]\displaystyle{ \frac{16}{33} }[/math] [math]\displaystyle{ \frac{-4}{33} }[/math]⟩—shares at least one thing in common with other JI intervals such as [math]\displaystyle{ \frac21 }[/math] [1 0 0⟩, [math]\displaystyle{ \frac{81}{40} }[/math] [-3 4 -1⟩, and [math]\displaystyle{ \frac{160}{81} }[/math] [5 -4 1⟩: they all get mapped to [1 0} by this meantone mapping matrix [math]\displaystyle{ M }[/math]. Note that this is no guarantee that [[math]\displaystyle{ \frac{17}{33} }[/math] [math]\displaystyle{ \frac{16}{33} }[/math] [math]\displaystyle{ \frac{-4}{33} }[/math]⟩ is close to these intervals (in theory, we can add or subtract an indefinite number of temperament commas from an interval without altering what it maps to!), but it at least suggests that it's reasonably close to them, i.e. that it's about an octave in size.
And a similar statement can be made about the second column vector of [math]\displaystyle{ M^{+} }[/math], [[math]\displaystyle{ \frac{16}{33} }[/math] [math]\displaystyle{ \frac{17}{33} }[/math] [math]\displaystyle{ \frac{4}{33} }[/math]⟩, with respect to [math]\displaystyle{ \frac31 }[/math] [0 1 0⟩ and [math]\displaystyle{ \frac{80}{27} }[/math] [4 -3 1⟩, etc.: they all map to [0 1}, and so [[math]\displaystyle{ \frac{16}{33} }[/math] [math]\displaystyle{ \frac{17}{33} }[/math] [math]\displaystyle{ \frac{4}{33} }[/math]⟩ is probably about a perfect twelfth in size like the rest of them.
(In this case, both likelihoods are indeed true: our two tuned generators are 1202.607 ¢ and 696.741 ¢ in size.)
Example of when the pseudoinverse does not behave like a true inverse
Before we get to that, we should finish what we've got going here, and show for contrast what happens when we flip-flop [math]\displaystyle{ M }[/math] and [math]\displaystyle{ M^{+} }[/math], so that the [math]\displaystyle{ (3, 2) }[/math]-shaped rectangular pseudoinverse times the original [math]\displaystyle{ (2, 3) }[/math]-shaped rectangular matrix leads to a [math]\displaystyle{ (3, 3) }[/math]-shaped matrix which is not an identity matrix:
[math]\displaystyle{
\begin{array} {c}
M^{+} \\
\left[ \begin{array} {c}
\frac{17}{33} & \frac{16}{33} \\
\frac{16}{33} & \frac{17}{33} \\
-{\frac{4}{33}} & \frac{4}{33} \\
\end{array} \right]
\end{array}
\begin{array} {c}
M \\
\left[ \begin{array} {r}
1 & 0 & {-4} \\
0 & 1 & 4 \\
\end{array} \right]
\end{array}
\begin{array} {c} \\ = \end{array}
\begin{array} {c}
M^{+}M \\
\left[ \begin{array} {c}
\frac{17}{33} & \frac{16}{33} & {-\frac{4}{33}} \\
\frac{16}{33} & \frac{17}{33} & \frac{4}{33} \\
{-\frac{4}{33}} & \frac{4}{33} & \frac{32}{33} \\
\end{array} \right]
\end{array}
}[/math]
While this matrix [math]\displaystyle{ M^{+}M }[/math] clearly isn't an identity matrix, since it's not all zeros except for ones running along its main diagonal, and it doesn't really look anything like an identity matrix from a superficial perspective—just judging by the numbers we can read off its entries—it turns out that behavior-wise this matrix does actually work out to be as "close" to an identity matrix as we can get, at least in a certain sense. And since our goal with tuning this temperament was to approximate JI as closely as possible, from this certain mathematical perspective, this is the matrix that accomplishes that. But again, we'll get to why exactly this matrix is the one that accomplishes that in a little bit.
Un-simplifying
First, to show how we can un-simplify things. The insight leading to this choice of [math]\displaystyle{ G = M^{+} }[/math] was made under the simplifying circumstances of [math]\displaystyle{ W = I }[/math] (unity-weight damage) and [math]\displaystyle{ \mathrm{T} = \mathrm{T}_{\text{p}} = I }[/math] (primes as target-intervals). But nothing about those choices of [math]\displaystyle{ W }[/math] or [math]\displaystyle{ \mathrm{T} }[/math] affect how this method works; setting them to [math]\displaystyle{ I }[/math] was only to help us humans see the way forward. There's nothing stopping us now from using any other weights and target-intervals for [math]\displaystyle{ W }[/math] and [math]\displaystyle{ \mathrm{T} }[/math]; the concept behind this method holds. Choosing [math]\displaystyle{ G = \mathrm{T}W(M\mathrm{T}W)^{+} }[/math], that is, still finds for us the [math]\displaystyle{ p = 2 }[/math] optimization for the problem.
Demystifying the formula
One way to think about what's happening in the formula of the pseudoinverse uses a technique we might call the "transform-act-antitransform technique": we want to take some action, but we can't do it in the current state, so we transform into a state where we can, then we take the action, and we finish off by performing the opposite of the initial transformation so that we get back to more of a similar state to the one we began with, yet having accomplished the action we intended.
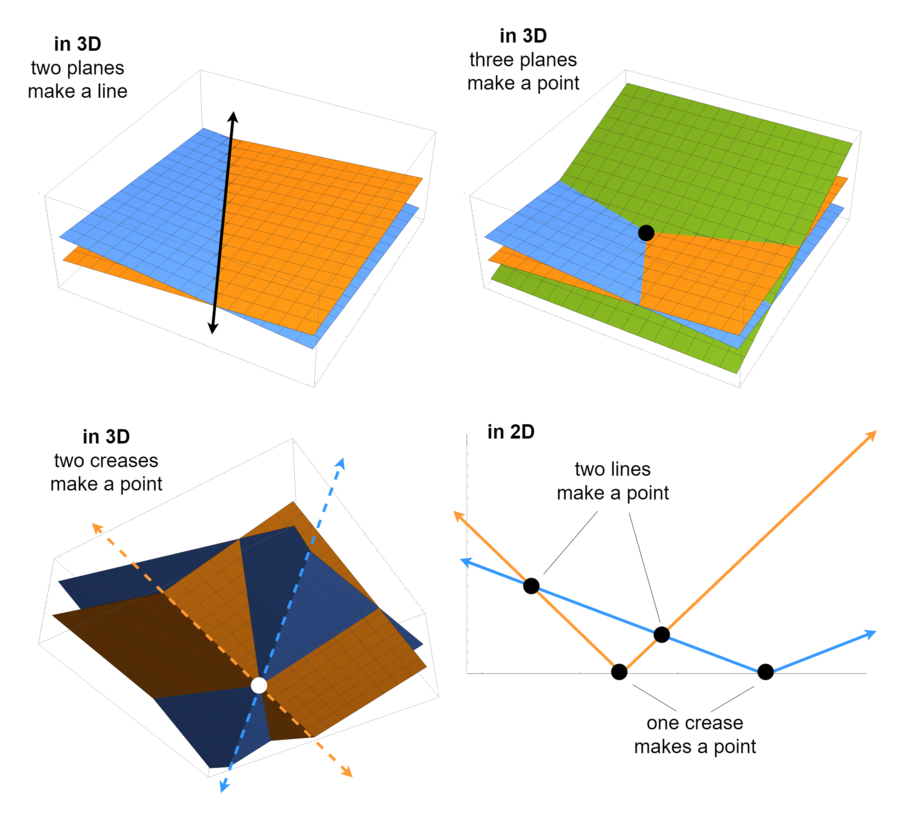
In the case of the pseudoinverse, the action we want to take is inverting a matrix. But we can't exactly invert it, because [math]\displaystyle{ A }[/math] is rectangular (to understand why, you can review the inversion process here: matrix inversion by hand). We happen to know that a matrix times its transpose is invertible, though (more on that in a moment), so:
- Multiplying by the matrix's transpose, finding [math]\displaystyle{ AA^\mathsf{T} }[/math], becomes our "transform" step.
- Then we invert like we wanted to do originally, so that's the "act" step: [math]\displaystyle{ (AA^\mathsf{T})^{-1} }[/math].
- Finally, we might think that we should multiply by the inverse of the matrix's transpose in order to undo our initial transformation step; however, we actually simply repeat the same thing, that is, we multiply by the transpose again! This is because we've put the matrix into an inverted state, so actually multiplying by the original's transpose here is essentially the opposite transformation. So that's the whole formula, then: [math]\displaystyle{ A^\mathsf{T}(AA^\mathsf{T})^{-1} }[/math].
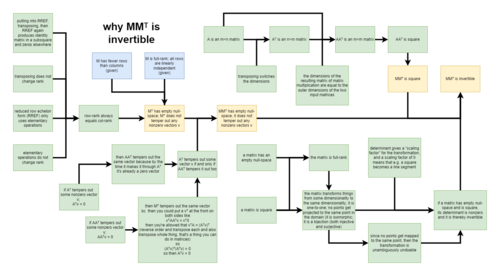
Now, as for why we know a matrix times its own transpose is invertible: there's a ton of little linear algebra facts that all converge to guarantee that this is so. Please consider the following diagram which lays all these facts all out at once.
Pseudoinverse: The "why"
In the previous section we took a look at how, mechanically, the pseudoinverse gives the solution for optimization power [math]\displaystyle{ p = 2 }[/math]. As for why, conceptually speaking, the pseudoinverse gives us the minimum point for the RMS graph in tuning damage space, it's sort of just one of those seemingly miraculously useful mathematical results. But we can try to give a basic explanation here.
Derivative, for slope
First, let's briefly go over some math facts. For some readers, these will be review:
- The slope of a graph means its rate of change. When slope is positive, the graph is going up, and when negative, it's going down.
- Wherever a graph has a local minimum or maximum, the slope is 0. That's because that's the point where it changes direction, between going up or down.
- We can find the slope at every point of a graph by taking its derivative.
So, considering that we want to find the minimum of a graph, one approach should be to find the derivative of this graph, then find the point(s) where its value is 0, which is where the slope is 0. This means those are the possible points where we have a local minimum, which means therefore that those are the points where we maybe have a global minimum, which is what we're after.
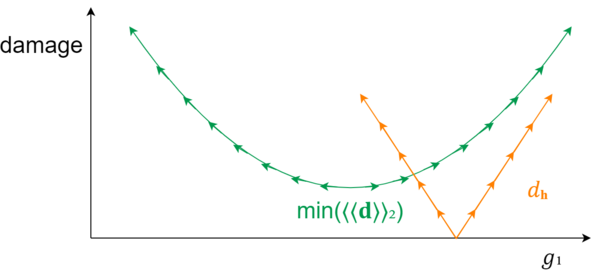
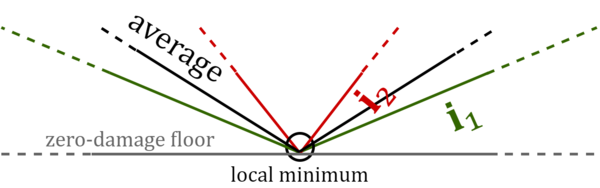
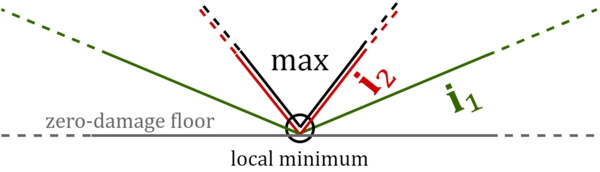
A unique minimum
As discussed in the tuning fundamentals article (in the section Non-unique tunings – power continuum), the graphs of mean damage and max damage—which are equivalent to the power means with powers [math]\displaystyle{ p = 1 }[/math] and [math]\displaystyle{ p = ∞ }[/math], respectively—consist of straight line segments connected by sharp corners, while all other optimization powers between [math]\displaystyle{ 1 }[/math] and [math]\displaystyle{ ∞ }[/math] form smooth curves. This is important because it is only for graphs with smooth curves that we can use its derivative to find the minimum point; the sharp corners of the other type of graph create discontinuities at those points, which in this context means points which have no definitive slope. The simple mathematical methods we use to find slope for smooth graphs get all confused and crash or give wrong results if we try to use them on these types of graphs.
So we can use the derivative slope technique for other powers [math]\displaystyle{ 1 \lt p \lt ∞ }[/math], but the pseudoinverse will only match the solution when [math]\displaystyle{ p = 2 }[/math].
And, spoiler alert: another key thing that's true about the [math]\displaystyle{ 2 }[/math]-mean graph whose minimum point we seek: it has only one point where the slope is equal 0, and it's our global minimum. Again, this is true of any of our curved [math]\displaystyle{ p }[/math]-mean graphs, but we only really care about it in the case of [math]\displaystyle{ p = 2 }[/math].
A toy example using the derivative
To get our feet on solid ground, let's just work through the math for an equal temperament example, i.e. one with only a single generator.
Kicking off with the setup discussed here, we have:
[math]\displaystyle{
\textbf{d} = 𝒋\,|\,(GM - G_{\text{j}}M_{\text{j}})\mathrm{T}W\,|
}[/math]
Let's rewrite this a tad, using the fact that [math]\displaystyle{ 𝒋G }[/math] is our generator tuning map [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ 𝒋G_{\text{j}}M_{\text{j}} }[/math] is equivalent to simply [math]\displaystyle{ 𝒋 }[/math]:
[math]\displaystyle{
\textbf{d} = |\,(𝒈M - 𝒋)\mathrm{T}W\,|
}[/math]
Let's say our rank-1 temperament is 12-ET, so our mapping [math]\displaystyle{ M }[/math] is ⟨12 19 28]. And our target-interval set is the otonal triad, so [math]\displaystyle{ \{ \frac54, \frac65, \frac32 \} }[/math]. And let's say we're complexity weighting, so [math]\displaystyle{ 𝒘 = \left[ \begin{array}{rrr} 4.322 & 4.907 & 2.585 \end{array} \right] }[/math], and [math]\displaystyle{ W }[/math] therefore is the diagonalized version of that (or [math]\displaystyle{ C }[/math] is the diagonlized version of [math]\displaystyle{ 𝒄 }[/math]). As for [math]\displaystyle{ 𝒈 }[/math], since this is a rank-1 temperament, being a [math]\displaystyle{ (1, r) }[/math]-shaped matrix, it's actually a [math]\displaystyle{ (1, 1) }[/math]-shaped matrix, and since we don't know what it is yet, it's single entry is the variable [math]\displaystyle{ g_1 }[/math]. This can be understood to represent the size of our ET generator in cents.
[math]\displaystyle{
\textbf{d} =
\Huge |
\normalsize
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
g_1 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
12 & 19 & 28 \\
\end{array} \right]
\end{array}
-
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r}
{-2} & 1 & {-1} \\
0 & 1 & 1 \\
1 & {-1} & 0 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
C \\
\left[ \begin{array} {rrr}
4.322 & 0 & 0 \\
0 & 4.907 & 0 \\
0 & 0 & 2.585 \\
\end{array} \right]
\end{array}
\Huge |
\normalsize
}[/math]
Here's what that looks like graphed:
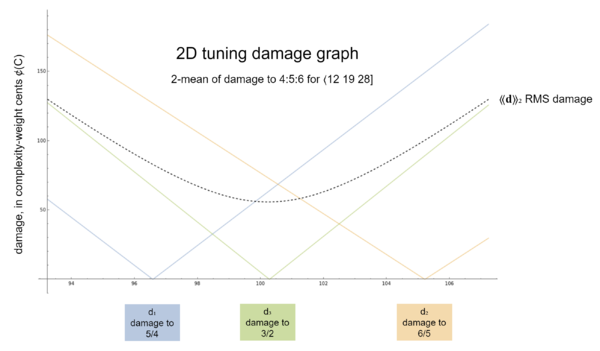
As alluded to earlier, for rank-1 cases, it's pretty easy to read the value straight off the chart. Clearly we're expecting a generator size that's just a smidge bigger than 100 ¢. The point is here to understand the computation process.
So, let's simplify:
[math]\displaystyle{
\textbf{d} =
\Huge |
\normalsize
\begin{array} {ccc}
𝒈M = 𝒕 \\
\left[ \begin{array} {rrr}
12g_1 & 19g_1 & 28g_1 \\
\end{array} \right]
\end{array}
-
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
\mathrm{T}C \\
\left[ \begin{array} {r|r|r}
{-8.644} & 4.907 & {-2.585} \\
0 & 4.907 & 2.585 \\
4.322 & {-4.907} & 0 \\
\end{array} \right]
\end{array}
\Huge |
\normalsize
}[/math]
Another pass:
[math]\displaystyle{ \textbf{d} = \Huge | \normalsize \begin{array} {ccc} 𝒕 - 𝒋 \\ \left[ \begin{array} {rrr} 12g_1 - 1200 & 19g_1 - 1901.955 & 28g_1 - 2786.31 \\ \end{array} \right] \end{array} \begin{array} {ccc} \mathrm{T}C \\ \left[ \begin{array} {r|r|r} {-8.644} & 4.907 & {-2.585} \\ 0 & 4.907 & 2.585 \\ 4.322 & {-4.907} & 0 \\ \end{array} \right] \end{array} \Huge | \normalsize }[/math]
And once more:
[math]\displaystyle{
\textbf{d} =
\Huge |
\normalsize
\begin{array} {ccc}
(𝒕 - 𝒋)\mathrm{T}C = 𝒓\mathrm{T}C = \textbf{e}C \\
\left[ \begin{array} {rrr}
17.288g_1 - 1669.605 &
14.721g_1 - 1548.835 &
18.095g_1 - 1814.526 \\
\end{array} \right]
\end{array}
\Huge |
\normalsize
}[/math]
And remember these bars are actually entry-wise absolute values, so we can put those on each entry. Though it actually won't matter much in a minute, since squaring things automatically causes positive values.
[math]\displaystyle{
\textbf{d} =
\begin{array} {ccc}
|\textbf{e}|C \\
\left[ \begin{array} {rrr}
|17.288g_1 - 1669.605| &
|14.721g_1 - 1548.835| &
|18.095g_1 - 1814.526| \\
\end{array} \right]
\end{array}
}[/math]
[math]\displaystyle{
% \slant{} command approximates italics to allow slanted bold characters, including digits, in MathJax.
\def\slant#1{\style{display:inline-block;margin:-.05em;transform:skew(-14deg)translateX(.03em)}{#1}}
% Latex equivalents of the wiki templates llzigzag and rrzigzag for double zigzag brackets.
\def\llzigzag{\hspace{-1.6mu}\style{display:inline-block;transform:scale(.62,1.24)translateY(.07em);font-family:sans-serif}{ꗨ\hspace{-3mu}ꗨ}\hspace{-1.6mu}}
\def\rrzigzag{\hspace{-1.6mu}\style{display:inline-block;transform:scale(-.62,1.24)translateY(.07em);font-family:sans-serif}{ꗨ\hspace{-3mu}ꗨ}\hspace{-1.6mu}}
}[/math]
Because what we're going to do now is change this to the formula for the SOS of damage, that is, [math]\displaystyle{ \llzigzag \textbf{d} \rrzigzag _2 }[/math]:
[math]\displaystyle{
\llzigzag \textbf{d} \rrzigzag _2 =
|17.288g_1 - 1669.605|^2 +
|14.721g_1 - 1548.835|^2 +
|18.095g_1 - 1814.526|^2
}[/math]
So we can get rid of those absolute value signs:
[math]\displaystyle{
\llzigzag \textbf{d} \rrzigzag _2 =
(17.288g_1 - 1669.605)^2 +
(14.721g_1 - 1548.835)^2 +
(18.095g_1 - 1814.526)^2
}[/math]
Then we're just going to work these out:
[math]\displaystyle{
\llzigzag \textbf{d} \rrzigzag _2 =
\small
(17.288g_1 - 1669.605)(17.288g_1 - 1669.605) +
(14.721g_1 - 1548.835)(14.721g_1 - 1548.835) +
(18.095g_1 - 1814.526)(18.095g_1 - 1814.526)
}[/math]
Distribute:
[math]\displaystyle{
\llzigzag \textbf{d} \rrzigzag _2 =
\small
(298.875g_1^2 - 57728.262g_1 - 2787580.856) +
(216.708g_1^2 - 45600.800g_1 - 2398889.857) +
(327.429g_1^2 - 65667.696g_1 - 3292504.605)
}[/math]
Combine like terms:
[math]\displaystyle{
\llzigzag \textbf{d} \rrzigzag _2 =
843.012g_1^2 - 168996.758g_1 - 8478975.318
}[/math]
At this point, we take the derivative. Basically, exponents decrease by 1 and what they were before turn into coefficients; we won't be doing a full review of this here, but good tutorials on that should be easy to find online.
[math]\displaystyle{
\dfrac{\partial}{\partial{g_1}}
\llzigzag \textbf{d} \rrzigzag _2 =
2×843.012g_1 - 168996.758
}[/math]
This is the formula for the slope of the graph, and we want to know where it's equal to zero.
[math]\displaystyle{
0 = 2×843.012g_1 - 168996.758
}[/math]
So we can now solve for [math]\displaystyle{ g_1 }[/math]:
[math]\displaystyle{
\begin {align}
0 &= 1686.024g_1 - 168996.758 \\[4pt]
168996.758 &= 1686.024g_1 \\[6pt]
\dfrac{168996.758}{1686.024} &= g_1 \\[6pt]
100.234 &= g_1 \\
\end {align}
}[/math]
Ta-da! There's our generator size: 100.234 ¢.[note 2]
Verifying the toy example with the pseudoinverse
Okay... but what the heck does this have to do with a pseudoinverse? Well, for a sanity check, let's double-check against our pseudoinverse method.
[math]\displaystyle{
G = \mathrm{T}W(M\mathrm{T}C)^{+} = \mathrm{T}C(M\mathrm{T}C)^\mathsf{T}(M\mathrm{T}C(M\mathrm{T}C)^\mathsf{T})^{-1}
}[/math]
We already know [math]\displaystyle{ \mathrm{T}C }[/math] from an earlier step above. And so [math]\displaystyle{ M\mathrm{T}C }[/math] is:
[math]\displaystyle{ \begin{array} {ccc} M \\ \left[ \begin{array} {rrr} 12 & 19 & 28 \\ \end{array} \right] \end{array} \begin{array} {ccc} \mathrm{T}C \\ \left[ \begin{array} {r|r|r} {-8.644} & 4.907 & {-2.585} \\ 0 & 4.907 & 2.585 \\ 4.322 & {-4.907} & 0 \\ \end{array} \right] \end{array} = \begin{array} {ccc} M\mathrm{T}C \\ \left[ \begin{array} {r|r|r} 17.288 & 14.721 & 18.095 \\ \end{array} \right] \end{array} }[/math]
So plugging these in we get:
[math]\displaystyle{
G =
\begin{array} {ccc}
\mathrm{T}C \\
\left[ \begin{array} {r|r|r}
{-8.644} & 4.907 & {-2.585} \\
0 & 4.907 & 2.585 \\
4.322 & {-4.907} & 0 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
(M\mathrm{T}C)^\mathsf{T} \\
\left[ \begin{array} {rrr}
17.288 \\ \hline
14.721 \\ \hline
18.095 \\
\end{array} \right]
\end{array}
(
\begin{array} {ccc}
M\mathrm{T}C \\
\left[ \begin{array} {r|r|r}
17.288 & 14.721 & 18.095 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
(M\mathrm{T}C)^\mathsf{T} \\
\left[ \begin{array} {rrr}
17.288 \\ \hline
14.721 \\ \hline
18.095 \\
\end{array} \right]
\end{array}
)^{-1}
}[/math]
Which works out to:
[math]\displaystyle{
G =
\begin{array} {ccc}
\mathrm{T}C(M\mathrm{T}C)^\mathsf{T} \\
\left[ \begin{array} {rrr}
527.565 \\
608.962 \\
642.322 \\
\end{array} \right]
\end{array}
(
\begin{array} {ccc}
M\mathrm{T}C(M\mathrm{T}C)^\mathsf{T} \\
\left[ \begin{array} {rrr}
842.983
\end{array} \right]
\end{array}
)^{-1}
}[/math]
Then take the inverse (interestingly, since this is a [math]\displaystyle{ (1, 1) }[/math]-shaped matrix, this is equivalent to the reciprocal, that is, we're just finding [math]\displaystyle{ \frac{1}{842.983} = 0.00119 }[/math]:
[math]\displaystyle{
G =
\begin{array} {ccc}
\mathrm{T}C(M\mathrm{T}C)^\mathsf{T} \\
\left[ \begin{array} {rrr}
{-123.974} \\
119.007 \\
2.484 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
(M\mathrm{T}C(M\mathrm{T}C)^\mathsf{T})^{-1} \\
\left[ \begin{array} {rrr}
0.00119
\end{array} \right]
\end{array}
}[/math]
And finally multiply:
[math]\displaystyle{
G =
\begin{array} {ccc}
\mathrm{T}C(M\mathrm{T}C)^\mathsf{T}(M\mathrm{T}C(M\mathrm{T}C)^\mathsf{T})^{-1} \\
\left[ \begin{array} {rrr}
{-0.147066} \\
0.141174 \\
0.002946 \\
\end{array} \right]
\end{array}
}[/math]
To compare with our 100.234 ¢ value, we'll have to convert this [math]\displaystyle{ G }[/math] to a [math]\displaystyle{ 𝒈 }[/math], but that's easy enough. As we demonstrated earlier, simply multiply by [math]\displaystyle{ 𝒋 }[/math]:
[math]\displaystyle{
𝒈 =
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
G \\
\left[ \begin{array} {rrr}
{-0.147066} \\
0.141174 \\
0.002946 \\
\end{array} \right]
\end{array}
}[/math]
When we work through that, we get 100.236 ¢. Close enough (shrugging off rounding errors). So we've sanity-checked at least.
But if we really want to see the connection between the pseudoinverse and the finding the zero of the derivative—how they both find the point where the slope of the RMS graph is zero and therefore it is at its minimum—we're going to have to upgrade from an equal temperament (rank-1 temperament) to a rank-2 temperament. In other words, we need to address tunings with more than one generator, ones can't be represented by a simple scalar anymore, but instead need to be represented with a vector.
A demonstration using matrix calculus
Technically speaking, even with two generators, meaning two variables, we could take the derivative with respect to one, and then take the derivative with respect to the other. And with three generators we could take three derivatives. But this gets out of hand. And there's a cleverer way we can think about the problem, which involves treating the vector containing all the generators as a single variable. We can do that! But it involves matrix calculus. And in this section we'll work through how.
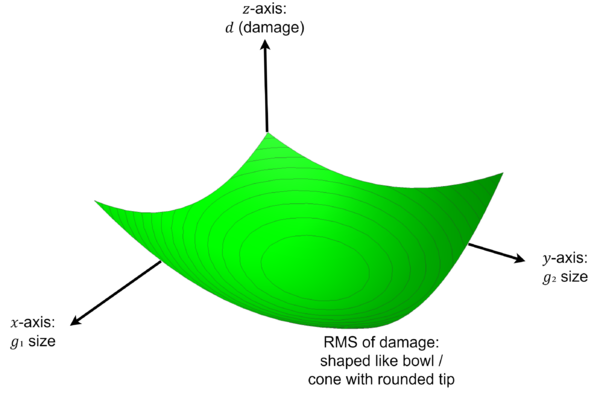
Graphing damage for a rank-2 temperament, as we've seen previously, means we'll be looking at 3D tuning damage space, with the [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] axes in perpendicular directions across the floor, and the [math]\displaystyle{ z }[/math]-axis coming up out of the floor, where the [math]\displaystyle{ x }[/math]-axis gives the tuning of one generator, the [math]\displaystyle{ y }[/math]-axis gives the tuning of the other generator, and the [math]\displaystyle{ z }[/math]-axis gives the temperament's damage as a function of those two generator tunings.
And while in 2D tuning damage space the RMS graph made something like a V-shape but with the tip rounded off, here it makes a cone, again with its tip rounded off.
Remember that although we like to think of it, and visualize it as minimizing the [math]\displaystyle{ 2 }[/math]-mean of damage, it's equivalent, and simpler computationally, to minimize the [math]\displaystyle{ 2 }[/math]-sum. So here's our function:
[math]\displaystyle{ f(x, y) = \llzigzag \textbf{d} \rrzigzag _2 }[/math]
Which is the same as:
[math]\displaystyle{ f(x, y) = \textbf{d}\textbf{d}^\mathsf{T} }[/math]
Because:
[math]\displaystyle{
\textbf{d}\textbf{d}^\mathsf{T} = \\
\textbf{d}·\textbf{d} = \\
\mathrm{d}_1·\mathrm{d}_1 + \mathrm{d}_2·\mathrm{d}_2 + \mathrm{d}_3·\mathrm{d}_3 = \\
\mathrm{d}_1^2 + \mathrm{d}_2^2 + \mathrm{d}_3^2
}[/math]
Which is the same thing as the [math]\displaystyle{ 2 }[/math]-sum: it's the sum of entries to the 2nd power.
Alright, but I can expect you may be concerned: [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] do not even appear in the body of the formula! Well, we can fix that.
As a first step toward resolving this problem, let's choose some better variable names. We had only chosen [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] because those are the most generic variable names available. They're very typically used when graphing things in Euclidean space like this. But we can definitely do better than those names, if we bring in some information more specific to our problem.
One thing we know is that these [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] variables are supposed to represent the tunings of our two generators. So let's call them [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math] instead:
[math]\displaystyle{ f(g_1, g_2) = \textbf{d}\textbf{d}^\mathsf{T} }[/math]
But we can do even better than this. We're in a world of vectors, so why not express [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math] together as a vector, [math]\displaystyle{ 𝒈 }[/math]. In other words, they're just a generator tuning map.
[math]\displaystyle{ f(𝒈) = \textbf{d}\textbf{d}^\mathsf{T} }[/math]
You may not be comfortable with the idea of a function of a vector (Douglas: I certainly wasn't when I first saw this!) but after working through this example and meditating on it for a while, you may be surprised to find it ceasing to seem so weird after all.
So we're still trying to connect the left and right sides of this equation by showing explicitly how this is a function of [math]\displaystyle{ 𝒈 }[/math], i.e. how [math]\displaystyle{ \textbf{d} }[/math] can be expressed in terms of [math]\displaystyle{ 𝒈 }[/math]. And we promise, we will get there soon enough.
Next, let's substitute in [math]\displaystyle{ (𝒕 - 𝒋)\mathrm{T}W }[/math] for [math]\displaystyle{ \textbf{d} }[/math]. In other words, the target-interval damage list is the difference between how the tempered-prime tuning map and the just-prime tuning map tune our target-intervals, absolute valued, and weighted by each interval's weight. But the amount of symbols necessary to represent this equation is going to get out of hand if we do exactly like this, so we're actually going to distribute first, finding [math]\displaystyle{ 𝒕\mathrm{T}W - 𝒋\mathrm{T}W }[/math], and then we're going to start following a pattern here of using Fraktur-style letters to represent matrices that are multiplied by [math]\displaystyle{ \mathrm{T}W }[/math], so that in our case [math]\displaystyle{ 𝖙 = 𝒕\mathrm{T}W }[/math] and [math]\displaystyle{ 𝖏 = 𝒋\mathrm{T}W }[/math]:
[math]\displaystyle{ f(𝒈) = (𝖙 - 𝖏)(𝖙^\mathsf{T} - 𝖏^\mathsf{T}) }[/math]
Now let's distribute these two binomials (you know, the old [math]\displaystyle{ (a + b)(c + d) = ac + ad + bc + bd }[/math] trick, AKA "FOIL" = first, outer, inner, last).
[math]\displaystyle{ f(𝒈) = 𝖙𝖙^\mathsf{T} - 𝖙𝖏^\mathsf{T} - 𝖏𝖙^\mathsf{T} + 𝖏𝖏^\mathsf{T} }[/math]
Because both [math]\displaystyle{ 𝖙𝖏^\mathsf{T} }[/math] and [math]\displaystyle{ 𝖏𝖙^\mathsf{T} }[/math] correspond to the dot product of [math]\displaystyle{ 𝖙 }[/math] and [math]\displaystyle{ 𝖏 }[/math], we can consolidate the two inner terms. Let's change [math]\displaystyle{ 𝖙𝖏^\mathsf{T} }[/math] into [math]\displaystyle{ 𝖏𝖙^\mathsf{T} }[/math], so that we will end up with [math]\displaystyle{ 2𝖏𝖙^\mathsf{T} }[/math] in the middle:
[math]\displaystyle{ f(𝒈) = 𝖙𝖙^\mathsf{T} - 2𝖏𝖙^\mathsf{T} + 𝖏𝖏^\mathsf{T} }[/math]
Alright! We're finally ready to surface [math]\displaystyle{ 𝒈 }[/math]. It's been hiding in [math]\displaystyle{ 𝒕 }[/math] all along; the tuning map is equal to the generator tuning map times the mapping, i.e. [math]\displaystyle{ 𝒕 = 𝒈M }[/math]. So we can just substitute that in everywhere. Exactly what we'll do is [math]\displaystyle{ 𝖙 = 𝒕\mathrm{T}W = (𝒈M)\mathrm{T}W = 𝒈(M\mathrm{T}W) = 𝒈𝔐 }[/math], that last step introducing a new Fraktur-style symbol.[note 3]
[math]\displaystyle{ f(𝒈) = (𝒈𝔐)(𝒈𝔐)^\mathsf{T} - 2𝖏(𝒈𝔐)^\mathsf{T} + 𝖏𝖏^\mathsf{T} }[/math]
And that gets sort of clunky, so let's execute some of those transposes. Note that when we transpose, the order of things reverses, so [math]\displaystyle{ (𝒈𝔐)^\mathsf{T} = 𝔐^\mathsf{T}𝒈^\mathsf{T} }[/math]:
[math]\displaystyle{ f(𝒈) = 𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 2𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + 𝖏𝖏^\mathsf{T} }[/math]
And now, we're finally ready to take the derivative!
[math]\displaystyle{ \dfrac{\partial}{\partial𝒈}f(𝒈) = \dfrac{\partial}{\partial𝒈}(𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 2𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + 𝖏𝖏^\mathsf{T}) }[/math]
And remember, we want to find the place where this function is equal to zero. So let's drop the [math]\displaystyle{ \dfrac{\partial}{\partial𝒈}f(𝒈) }[/math] part on the left, and show the [math]\displaystyle{ = \textbf{0} }[/math] part on the right instead (note the boldness of the [math]\displaystyle{ \textbf{0} }[/math]; this indicates that this is not simply a single zero, but a vector of all zeros, one for each generator).
[math]\displaystyle{ \dfrac{\partial}{\partial𝒈}(𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 2𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + 𝖏𝖏^\mathsf{T}) = \textbf{0} }[/math]
Well, now we've come to it. We've run out of things we can do without confronting the question: how in the world do we take derivatives of matrices? This next part is going to require some of that matrix calculus we warned about. Fortunately, if one is previously familiar with normal algebraic differentiation rules, these will not seem too wild:
- The last term, [math]\displaystyle{ 𝖏𝖏^\mathsf{T} }[/math], is going to vanish, because with respect to [math]\displaystyle{ 𝒈 }[/math], it's a constant; there's no factor of [math]\displaystyle{ 𝒈 }[/math] in it.
- The middle term, [math]\displaystyle{ -2𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} }[/math], has a single factor of [math]\displaystyle{ 𝒈 }[/math], so it will remain but with that factor gone. (Technically it's a factor of [math]\displaystyle{ 𝒈^\mathsf{T} }[/math], but for reasons that would probably require a deeper understanding of the subtleties of matrix calculus than the present author commands, it works out this way anyway. Perhaps we should have differentiated instead with respect to [math]\displaystyle{ 𝒈^\mathsf{T} }[/math], rather than [math]\displaystyle{ 𝒈 }[/math]?)[note 4]
- The first term, [math]\displaystyle{ 𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} }[/math], can in a way be seen to have a [math]\displaystyle{ 𝒈^2 }[/math], because it contains both a [math]\displaystyle{ 𝒈 }[/math] as well as a [math]\displaystyle{ 𝒈^\mathsf{T} }[/math] (and we demonstrated earlier how for a vector [math]\displaystyle{ \textbf{v} }[/math], there is a relationship between itself squared and it times its transpose); so, just as an [math]\displaystyle{ x^2 }[/math] differentiates to a [math]\displaystyle{ 2x }[/math], that is, the power is reduced by 1 and multiplies into any existing coefficient, this term becomes [math]\displaystyle{ 2𝒈𝔐𝔐^\mathsf{T} }[/math].
And so we find:
[math]\displaystyle{ 2𝒈𝔐𝔐^\mathsf{T} - 2𝖏𝔐^\mathsf{T} = \textbf{0} }[/math]
That's much nicer to look at, huh. Well, what next? Our goal is to solve for [math]\displaystyle{ 𝒈 }[/math], right? Then let's isolate the solitary remaining term with [math]\displaystyle{ 𝒈 }[/math] as a factor on one side of the equation:
[math]\displaystyle{ 2𝒈𝔐𝔐^\mathsf{T} = 2𝖏𝔐^\mathsf{T} }[/math]
Certainly we can cancel out the 2's on both sides; that's easy:
[math]\displaystyle{ 𝒈𝔐𝔐^\mathsf{T} = 𝖏𝔐^\mathsf{T} }[/math]
And, as we proved in the earlier section "Demystifying the formula", [math]\displaystyle{ AA^\mathsf{T} }[/math] is invertible, so we cancel that out on the left by multiplying both sides of the equation by [math]\displaystyle{ (𝔐𝔐^\mathsf{T})^{-1} }[/math]:
[math]\displaystyle{
𝒈𝔐𝔐^\mathsf{T}(𝔐𝔐^\mathsf{T})^{-1} = 𝖏𝔐^\mathsf{T}(𝔐𝔐^\mathsf{T})^{-1} \\
𝒈\cancel{𝔐𝔐^\mathsf{T}}\cancel{(𝔐𝔐^\mathsf{T})^{-1}} = 𝖏𝔐^\mathsf{T}(𝔐𝔐^\mathsf{T})^{-1} \\
𝒈 = 𝖏𝔐^\mathsf{T}(𝔐𝔐^\mathsf{T})^{-1}
}[/math]
Finally, remember that [math]\displaystyle{ 𝒈 = 𝒋G }[/math] and [math]\displaystyle{ 𝒋 = 𝒋G_{\text{j}}M_{\text{j}} }[/math], so we can replace those and cancel out some more stuff (also remember that [math]\displaystyle{ 𝖏 = 𝒋\mathrm{T}W }[/math]):
[math]\displaystyle{
(𝒋G) = (𝒋G_{\text{j}}M_{\text{j}})\mathrm{T}W𝔐^\mathsf{T}(𝔐𝔐^\mathsf{T})^{-1} \\
\cancel{𝒋}G = \cancel{𝒋}\cancel{I}\cancel{I}\mathrm{T}W𝔐^\mathsf{T}(𝔐𝔐^\mathsf{T})^{-1}
}[/math]
And that part on the right looks pretty familiar...
[math]\displaystyle{
G = \mathrm{T}W𝔐^\mathsf{T}(𝔐𝔐^\mathsf{T})^{-1} \\
G = \mathrm{T}W𝔐^{+} \\
G = \mathrm{T}W(M\mathrm{T}W)^{+}
}[/math]
Voilà! We've found our pseudoinverse-based [math]\displaystyle{ G }[/math] formula, finding it to be the [math]\displaystyle{ G }[/math] that gives the point of zero slope, i.e. the minimum point of the RMS damage graph.
If you're hungry for more information on these concepts, or even just another take on it, please see User:Sintel/Generator optimization#Least squares method.
With held-intervals
The pseudoinverse method can be adapted to handle tuning schemes which have held-intervals. The basic idea here is that we can no longer simply grab the tuning found as the point at the bottom of the tuning damage graph bowl hovering above the floor, because that tuning probably doesn't also happen to be one that leaves the requested interval unchanged. We can imagine an additional feature in our tuning damage space: the line across this bowl which connects every point where the generator tunings work out such that our interval is indeed unchanged. Again, this line probably doesn't straight through the bottommost point of our RMS-damage graph. But that's okay. That just means we could still decrease the overall damage further if we didn't hold the interval unchanged. But assuming we're serious about holding this interval unchanged, we've simply modified the problem a bit. Now we're looking for the point along this new held-interval line which is closest to the floor. Simple enough to understand, in concept! The rest of this section is dedicated to explaining how, mathematically speaking, we're able to identify that point. It still involves matrix calculus—derivatives of vectors, and such—but now we also pull in some additional ideas. We hope you dig it.[note 5]
We'll be talking through this problem assuming a three-dimensional tuning damage graph, which is to say, we're dealing with a rank-2 temperament (the two generator dimensions across the floor, and the damage dimension up from the floor). If we asked for more than one interval to be held unchanged, then we'd flip over to the "only held-intervals" method discussed later, because at that point there's only a single possible tuning. And if we asked for less than one interval to be held unchanged, then we'd be back to the ordinary pseudoinverse method which you've already learned. So for this extended example we'll be assuming one held-interval. But the principles discussed here generalize to higher dimensions of temperaments and more held-intervals, if the dimensionality supports them. These higher dimensional examples are more difficult to visualize, though, of course, and so we've chosen the simplest possibility that sufficiently demonstrates the ideas we need to learn.
Topographic view
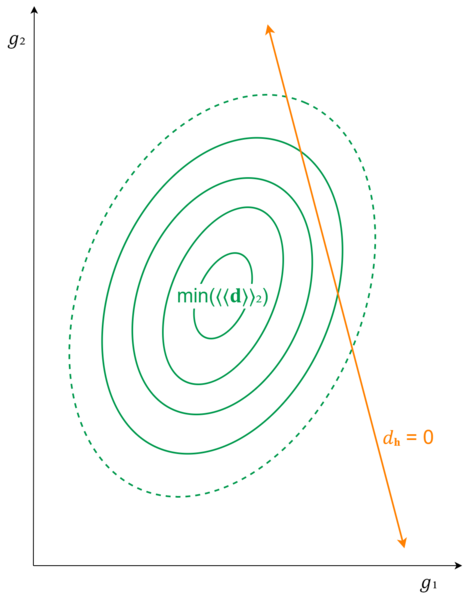
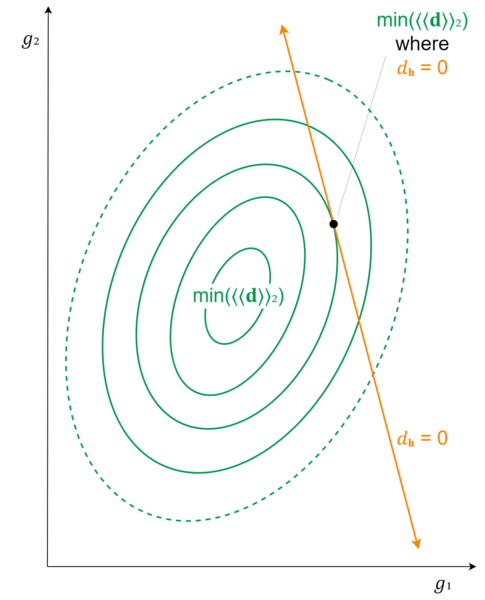
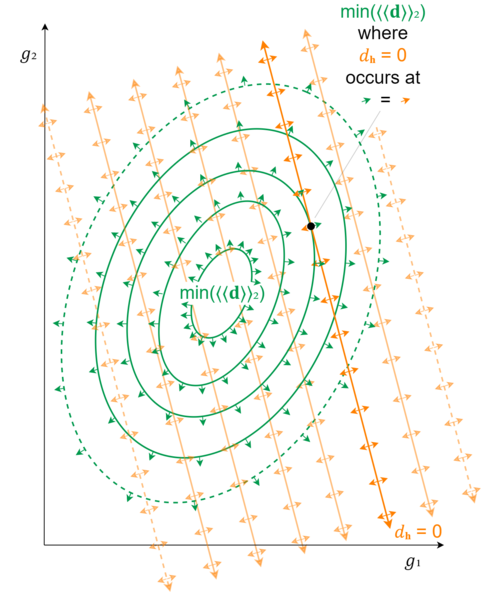
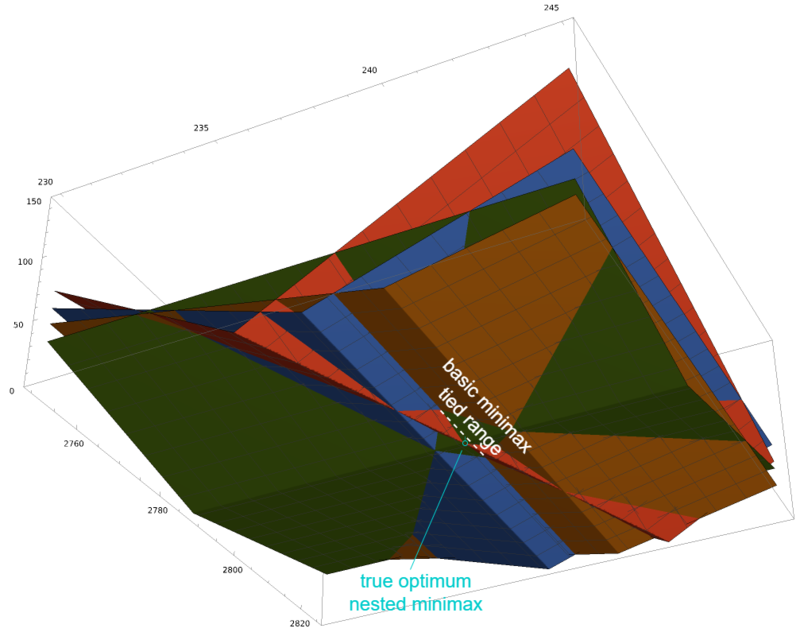
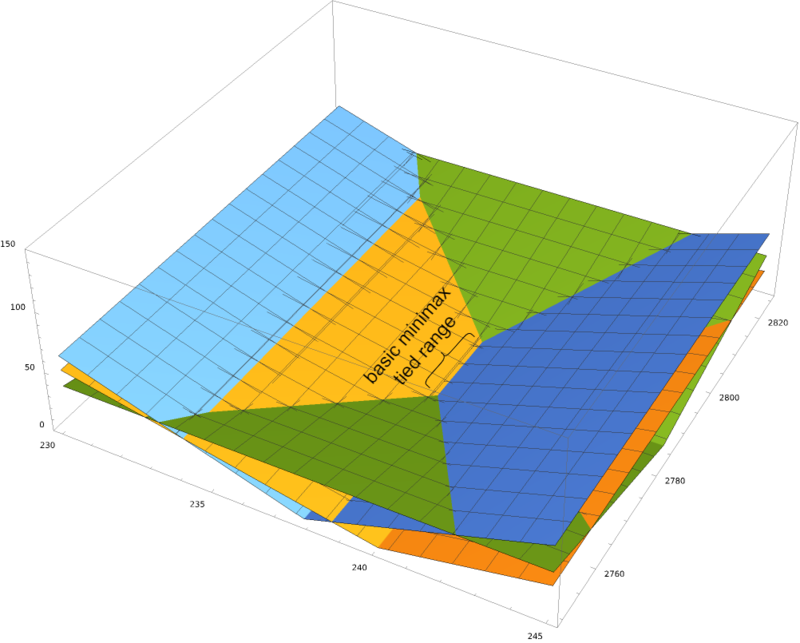
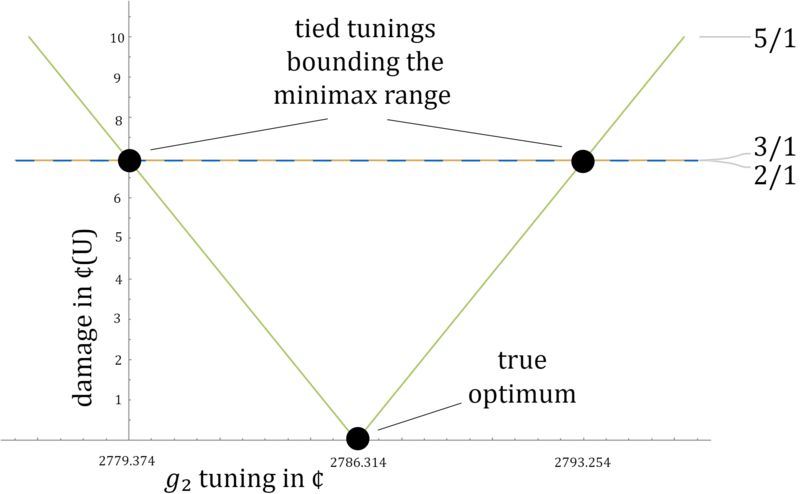
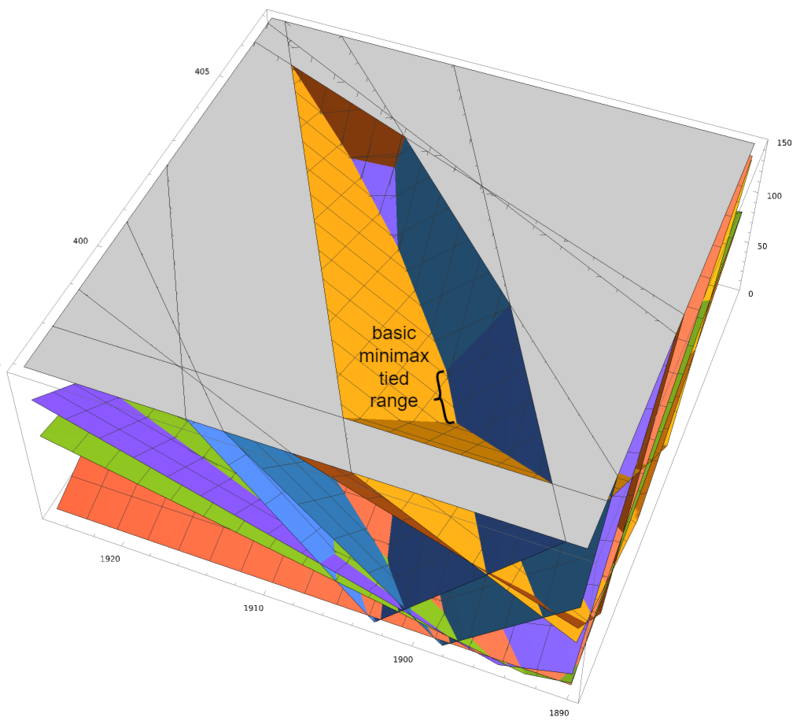
[math]\displaystyle{ % Latex equivalents of the wiki templates llzigzag and rrzigzag for double zigzag brackets. % Annoyingly, we need slightly different Latex versions for the different Latex sizes. \def\smallLLzigzag{\hspace{-1.4mu}\style{display:inline-block;transform:scale(.62,1.24)translateY(.05em);font-family:sans-serif}{ꗨ\hspace{-2.6mu}ꗨ}\hspace{-1.4mu}} \def\smallRRzigzag{\hspace{-1.4mu}\style{display:inline-block;transform:scale(-.62,1.24)translateY(.05em);font-family:sans-serif}{ꗨ\hspace{-2.6mu}ꗨ}\hspace{-1.4mu}} \def\llzigzag{\hspace{-1.6mu}\style{display:inline-block;transform:scale(.62,1.24)translateY(.07em);font-family:sans-serif}{ꗨ\hspace{-3mu}ꗨ}\hspace{-1.6mu}} \def\rrzigzag{\hspace{-1.6mu}\style{display:inline-block;transform:scale(-.62,1.24)translateY(.07em);font-family:sans-serif}{ꗨ\hspace{-3mu}ꗨ}\hspace{-1.6mu}} \def\largeLLzigzag{\hspace{-1.8mu}\style{display:inline-block;transform:scale(.62,1.24)translateY(.09em);font-family:sans-serif}{ꗨ\hspace{-3.5mu}ꗨ}\hspace{-1.8mu}} \def\largeRRzigzag{\hspace{-1.8mu}\style{display:inline-block;transform:scale(-.62,1.24)translateY(.09em);font-family:sans-serif}{ꗨ\hspace{-3.5mu}ꗨ}\hspace{-1.8mu}} \def\LargeLLzigzag{\hspace{-2.5mu}\style{display:inline-block;transform:scale(.62,1.24)translateY(.1em);font-family:sans-serif}{ꗨ\hspace{-4.5mu}ꗨ}\hspace{-2.5mu}} \def\LargeRRzigzag{\hspace{-2.5mu}\style{display:inline-block;transform:scale(-.62,1.24)translateY(.1em);font-family:sans-serif}{ꗨ\hspace{-4.5mu}ꗨ}\hspace{-2.5mu}} }[/math] Back in the fundamentals article, we briefly demonstrated a special way to visualize a 3-dimensional tuning damage 2-dimensionally: in a topographic view, where the [math]\displaystyle{ z }[/math]-axis is pointing straight out of the page, and represented by contour lines tracing out the shapes of points which share the same [math]\displaystyle{ z }[/math]-value. In the case of a tuning damage graph, then, this will show concentric rings (not necessarily circles) around the lowest point of our damage bowl, representing how damage increases smoothly in any direction you take away from that minimum point. So far we haven't made much use of this visualization approach, but for tuning schemes with [math]\displaystyle{ p=2 }[/math] and at least one held-interval, it's the perfect tool for the job.
So now we draw our held-interval line across this topographic view.
Our first guess at the lowest point on this line might be the point closest to the actual minimum damage. Good guess, but not necessarily true. It would be true if the rings were exactly circles. But they're not necessarily; they might be oblong, and the skew may not be in an obvious angle with respect to the held-interval line. So for a generalized means of finding the lowest point on the held-interval line, we need to think a bit deeper about the problem.
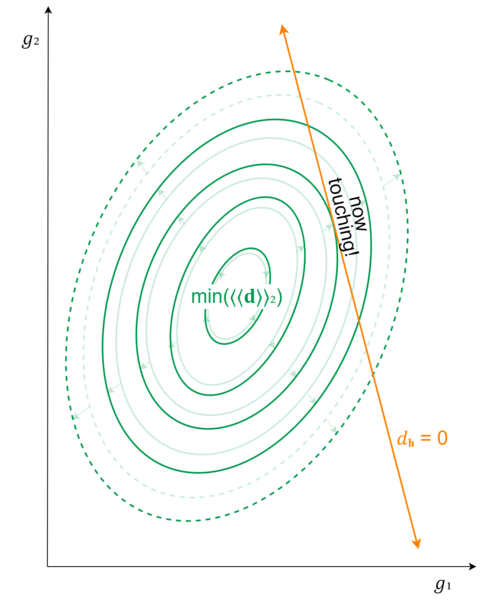
The first step to understanding better is to adjust our contour lines. The obvious place to start was at increments of 1 damage. But we're going to want to rescale so that one of our contour lines exactly touches the held-interval line. To be clear, we're not changing the damage graph at all; we're simply changing how we visualize it on this topographic view.
The point where this contour line touches the held-interval line, then, is the lowest point on the held-interval line, that is, the point among all those where the held-interval is indeed unchanged where the overall damage to the target-intervals is the least. This should be easy enough to see, because if you step just an infinitesimally small amount in either direction along the held-interval line, you will no longer be touching the contour line, but rather you will be just outside of it, which means you have slightly higher damage than whatever constant damage amount that contour traces.
Next, we need to figure out how to identify this point. It may seem frustrating, because we're looking right at it! But we don't already have formulas for these contour lines.
Matching slopes
In order to identify this point, it's going to be more helpful to look at the entire graph of our held-interval's error. That is, rather than only drawing the line where it's zero:
[math]\displaystyle{
𝒕\mathrm{H} - 𝒋\mathrm{H} = 0
}[/math]
We'll draw the whole thing:
[math]\displaystyle{
𝒕\mathrm{H} - 𝒋\mathrm{H}
}[/math]
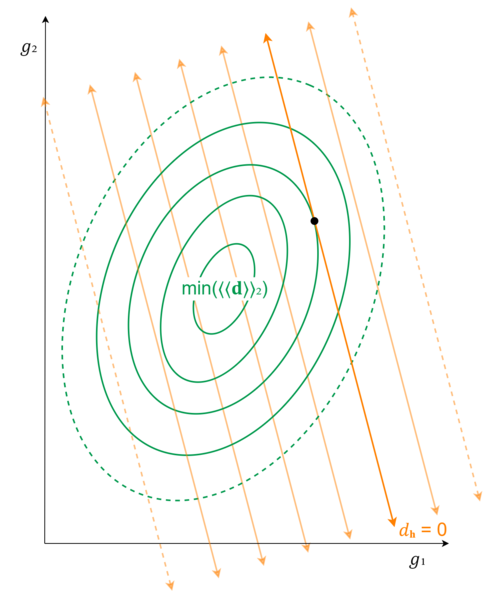
If the original graph was like a line drawn diagonally across the floor, the full graph looks like this but with a plane running through it, tilted, on one side ascending up and out from the floor, on the other side descending down and into the floor. In the topographic view, then, this graph will appear as equally-spaced parallel lines to the original line, emanating outwards in both directions from it.
The next thing we want to see are some little arrows along all of these contour lines, both for the damage graph and for the held-interval graph, which point perpendicularly to them.
What these little arrows represent are the derivatives of these graphs at those points, or in other words, the slope. If this isn't clear, it might help to step back for a moment to 2D, and draw little arrows in a similar fashion:
In higher dimensions, the generalized way to think about slope is that it's the vector pointing in the direction of steepest slope upwards from the given point.
Now, we're not attempting to distinguish the sizes of these slopes here. We could do that, perhaps by changing the relative scale of the arrows. But that's particularly important for our purposes. We only need to notice the different directions these slopes point.
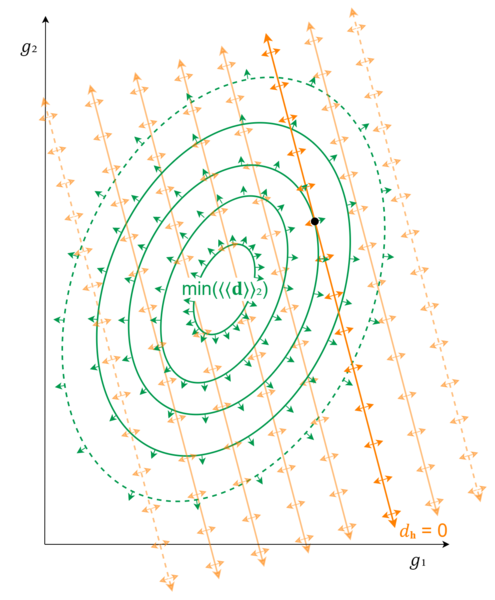
You may recall that in the simpler case—with no held-intervals—we identified the point at the bottom of the bowl using derivatives; this point is where the derivative (slope) is equal to zero. Well, what can we notice about the point we're seeking to identify? It's where the slopes of the RMS damage graph for the target-intervals and the error of the held-interval match!
So, our first draft of our goal might look something like this:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈}}( \llzigzag \textbf{d} \rrzigzag _2) = \dfrac{\partial}{\partial{𝒈}}(𝒓\mathrm{H})
}[/math]
But that's not quite specific enough. To ensure we grab grab a point satisfying that condition, but also ensure that it's on our held-interval line, we could simply add another equation:
[math]\displaystyle{
\begin{align}
\dfrac{\partial}{\partial{𝒈}}( \llzigzag \textbf{d} \rrzigzag _2) &= \dfrac{\partial}{\partial{𝒈}}(𝒓\mathrm{H}) \\[12pt]
𝒓\mathrm{H} &= 0
\end{align}
}[/math]
But there's another special way of asking for the same thing, that isn't as obvious-looking, but consolidates it all down to a single equation, which—due to some mathemagic—eventually works out to give us a really nice solution. Here's what that looks like:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, λ}}( \llzigzag \textbf{d} \rrzigzag _2) = \dfrac{\partial}{\partial{𝒈, λ}}(λ𝒓\mathrm{H})
}[/math]
What we've done here is added a new variable [math]\displaystyle{ λ }[/math][note 6], a multiplier which scales the error in the interval we want to be unchanged. We can visualize its effect as saying: we don't care about the relative lengths of these two vectors; we only care about wherever they point in exactly the same direction. This trick works as long as we take the derivative with respect to [math]\displaystyle{ λ }[/math] as well, which you'll note we're doing now too.[note 7] We don't expect this to be clear straight away; the reason this works will probably only become clear in later steps of working through the problem.
Let's rework our equation a bit to make things nicer. One thing we can do is put both terms on one side of the equation, equalling zero (rather, the zero vector, with a bolded zero):
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, λ}}( \llzigzag \textbf{d} \rrzigzag _2) - \dfrac{\partial}{\partial{𝒈, λ}}(λ𝒓\mathrm{H}) = \textbf{0}
}[/math]
And now we can consolidate the derivatives:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, λ}}( \llzigzag \textbf{d} \rrzigzag _2 - λ𝒓\mathrm{H}) = \textbf{0}
}[/math]
We're going to switch from subtraction to addition here. How can we get away with that? Well, it just changes what [math]\displaystyle{ λ }[/math] comes out to; it'll just flip the sign on it. But we'll get the same answer either way. And we won't actually need to do anything with the value of [math]\displaystyle{ λ }[/math] in the end; we only need to know the answers to the generator sizes in [math]\displaystyle{ 𝒈 }[/math].
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, λ}}( \llzigzag \textbf{d} \rrzigzag _2 + λ𝒓\mathrm{H}) = \textbf{0}
}[/math]
Similarly, we can do this without changing the result:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, λ}}(\frac12 \llzigzag \textbf{d} \rrzigzag _2 + λ𝒓\mathrm{H}) = \textbf{0}
}[/math]
That'll make the maths work out nicer, and just means [math]\displaystyle{ λ }[/math] will be half the size as it would have been otherwise.
So: we're looking for the value of [math]\displaystyle{ 𝒈 }[/math]. But [math]\displaystyle{ 𝒈 }[/math] doesn't appear in the equation yet. That's because it's hiding inside [math]\displaystyle{ \textbf{d} }[/math] and [math]\displaystyle{ 𝒓 }[/math]. We won't bother repeating all the steps from the simpler case; we'll just replace [math]\displaystyle{ \llzigzag \textbf{d} \rrzigzag _2 }[/math] with [math]\displaystyle{ 𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 2𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + 𝖏𝖏^\mathsf{T} }[/math]. And as for [math]\displaystyle{ 𝒓 }[/math], that's just [math]\displaystyle{ 𝒕 - 𝒋 }[/math], or [math]\displaystyle{ 𝒈M - 𝒋 }[/math]. So we have:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, λ}}(\frac12(𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 2𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + 𝖏𝖏^\mathsf{T}) + λ(𝒈M - 𝒋)\mathrm{H}) = \textbf{0}
}[/math]
And let's just distribute stuff so we have a simple summation:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, λ}}(\frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + \frac12𝖏𝖏^\mathsf{T} + λ𝒈M\mathrm{H} - λ𝒋\mathrm{H}) = \textbf{0}
}[/math]
Everything in that expression other than [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ λ }[/math] are known values; only [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ λ }[/math] are variables.
As a final change, we're going to recognize the fact that for higher-dimensional temperaments, we might sometimes have multiple held-intervals. Which is to say that our new variable might actually itself be a vector! So we'll use a bold [math]\displaystyle{ \textbf{λ} }[/math] here to capture that idea.[note 8] (The example we will demonstrate with periodically will still only have one held-interval, though, but that's fine if this is a one-entry vector, whose only entry is [math]\displaystyle{ λ_1 }[/math].) Note that we need to locate [math]\displaystyle{ \textbf{λ} }[/math] on the right side of each term now, so that its [math]\displaystyle{ h }[/math] height matches up with the [math]\displaystyle{ h }[/math] width of [math]\displaystyle{ \mathrm{H} }[/math].
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, \textbf{λ}}}(\frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + \frac12𝖏𝖏^\mathsf{T} + 𝒈M\mathrm{H}\textbf{λ} - 𝒋\mathrm{H}\textbf{λ}) = \textbf{0}
}[/math]
Now in the simpler case, when we took the derivative simply with respect to [math]\displaystyle{ 𝒈 }[/math], we could almost treat the vectors and matrices like normal variables when taking derivatives: exponents came down as coefficients, and exponents decremented by 1. But now that we're taking the derivative with respect to both [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ \textbf{λ} }[/math], the clearest way forward is to understand this in terms of a system of equations, rather than a single equation of matrices and vectors.
Multiple derivatives
One way of thinking about what we're asking for with [math]\displaystyle{ \dfrac{\partial}{\partial{𝒈, \textbf{λ}}} }[/math] is that we want the vector whose entries are partial derivatives with respect to each scalar entry of [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ \textbf{λ} }[/math]. We hinted at this earlier when we introduced the bold-zero vector [math]\displaystyle{ \textbf{0} }[/math], which represented a zero for each generator. So if:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈}} \llzigzag \textbf{d} \rrzigzag _2 = \\
\dfrac{\partial}{\partial{𝒈}} ( 𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 2𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + 𝖏𝖏^\mathsf{T}) = \\
\dfrac{\partial}{\partial{𝒈}} f(𝒈) \\
}[/math]
Then if we find a miniRMS damage where [math]\displaystyle{ 𝒈 }[/math] = {1198.857 162.966], that tells us that:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈}} f(\left[ \begin{array} {c} 1198.857 & 162.966 \\ \end{array} \right]) = \textbf{0} = \left[ \begin{array} {c} 0 & 0 \\ \end{array} \right]
}[/math]
Or in other words:
[math]\displaystyle{
\dfrac{\partial}{\partial{g_1}} f(\left[ \begin{array} {c} 1198.857 & 162.966 \\ \end{array} \right]) = 0 \\
\dfrac{\partial}{\partial{g_2}} f(\left[ \begin{array} {c} 1198.857 & 162.966 \\ \end{array} \right]) = 0
}[/math]
And so if we plug in some other [math]\displaystyle{ 𝒈 }[/math] to [math]\displaystyle{ f() }[/math], what we get out is some vector [math]\displaystyle{ \textbf{v} }[/math] telling us the slope of the damage graph at the tuning represented by that generator tuning map:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈}} f(\left[ \begin{array} {c} 1200.000 & 163.316 \\ \end{array} \right]) = \textbf{v}
}[/math]
Or in other words:
[math]\displaystyle{
\dfrac{\partial}{\partial{g_1}} f(\left[ \begin{array} {c} 1200.000 & 163.316 \\ \end{array} \right]) = v_1 \\
\dfrac{\partial}{\partial{g_1}} f(\left[ \begin{array} {c} 1200.000 & 163.316 \\ \end{array} \right]) = v_2 \\
}[/math]
So when we ask for:
[math]\displaystyle{
\dfrac{\partial}{\partial{𝒈, \textbf{λ}}}(\frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + \frac12𝖏𝖏^\mathsf{T} + 𝒈M\mathrm{H}\textbf{λ} - 𝒋\mathrm{H}\textbf{λ}) = \textbf{0} = \left[ \begin{array} {c} 0 & 0 & 0 \\ \end{array} \right]
}[/math]
What we really want under the hood is the derivative with respect to [math]\displaystyle{ g_1 }[/math] to be 0, the derivative with respect to [math]\displaystyle{ g_2 }[/math] to be 0, and also the derivative with respect to [math]\displaystyle{ λ_1 }[/math] to be 0:
[math]\displaystyle{
\dfrac{\partial}{\partial{g_1}}(\frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + \frac12𝖏𝖏^\mathsf{T} + 𝒈M\mathrm{H}\textbf{λ} - 𝒋\mathrm{H}\textbf{λ}) = 0 \\
\dfrac{\partial}{\partial{g_2}}(\frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + \frac12𝖏𝖏^\mathsf{T} + 𝒈M\mathrm{H}\textbf{λ} - 𝒋\mathrm{H}\textbf{λ}) = 0 \\
\dfrac{\partial}{\partial{λ_1}}(\frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + \frac12𝖏𝖏^\mathsf{T} + 𝒈M\mathrm{H}\textbf{λ} - 𝒋\mathrm{H}\textbf{λ}) = 0 \\
}[/math]
So, this essentially gives us a vector whose entries are derivatives, and which can be thought of as an arrow in space pointing in the multidimensional direction of the slope of the graph at a point. Sometimes these vector derivatives are called "gradients" and notated with an upside-down triangle, but we're just going to stick with the more familiar algebraic terminology here for our purposes.
To give a quick and dirty answer to the question posed earlier regarding why introducing [math]\displaystyle{ \textbf{λ} }[/math] is a replacement of any sort for the obvious equation [math]\displaystyle{ 𝒓\mathrm{H} = 0 }[/math], notice what the derivative of the third equation will be. We'll work it out in rigorous detail soon, but for now, let's just observe how [math]\displaystyle{ \dfrac{\partial}{\partial{λ_1}}(\frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} - 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} + \frac12𝖏𝖏^\mathsf{T} + 𝒈M\mathrm{H}\textbf{λ} - 𝒋\mathrm{H}\textbf{λ}) = 𝒈M\mathrm{H} - 𝒋\mathrm{H} }[/math]. So if that's equal to 0, and [math]\displaystyle{ 𝒓 }[/math] can be rewritten as [math]\displaystyle{ 𝒕 - 𝒋 }[/math] and further as [math]\displaystyle{ 𝒈𝑀 - 𝒋 }[/math], then we can see how this has covered our bases re: [math]\displaystyle{ 𝒓\mathrm{H} = 0 }[/math], while also providing the connective tissue to the other equations re: using [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ \textbf{λ} }[/math] to minimize damage to our target-intervals; because [math]\displaystyle{ \textbf{λ} }[/math] figures in terms in the first two equations which also have a [math]\displaystyle{ 𝒈 }[/math] in them, so whatever it comes out to will affect those; this is how we achieve the offsetting from the actual bottom of the damage bowl.
Break down matrices
In order to work this out, though, we'll need to break our occurrences of [math]\displaystyle{ 𝒈 }[/math] down into [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math] (and [math]\displaystyle{ \textbf{λ} }[/math] down into [math]\displaystyle{ λ_1 }[/math]).
So let's take this daunting task on, one term at a time. Term one of five:
[math]\displaystyle{ \frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} }[/math]
Remember, [math]\displaystyle{ 𝔐 = M\mathrm{T}W }[/math]. We haven't specified our target-interval count [math]\displaystyle{ k }[/math]. Whatever it is, though, if we were to drill all the way down to the [math]\displaystyle{ m_{ij} }[/math], [math]\displaystyle{ t_{ij} }[/math], and [math]\displaystyle{ w_{ij} }[/math] level here as we are doing with [math]\displaystyle{ 𝒈 }[/math], then the entries of [math]\displaystyle{ 𝔐 }[/math] would be so complicated that they'd be hard to fit on the page, with dozens of summed up terms. And the entries of [math]\displaystyle{ 𝔐𝔐^\mathsf{T} }[/math] would be even crazier! So let's not.
Besides, we don't need to drill down into [math]\displaystyle{ M }[/math], [math]\displaystyle{ \mathrm{T} }[/math], or [math]\displaystyle{ W }[/math] in the same way we need to drill down into [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ \mathbf{λ} }[/math], because they're not variables we need to differentiate by; they're all just known constants, information about the temperament we're tuning and the tuning scheme according to which we're tuning it. So why would we drill down into those? Well, we won't.
Instead, let's take an approach where in each term, we'll multiply together every matrix other than [math]\displaystyle{ 𝒈 }[/math] and [math]\displaystyle{ \mathbf{λ} }[/math], then use letters [math]\displaystyle{ \mathrm{A} }[/math], [math]\displaystyle{ \mathrm{B} }[/math], [math]\displaystyle{ \mathrm{C} }[/math], [math]\displaystyle{ \mathrm{D} }[/math], and [math]\displaystyle{ \mathrm{E} }[/math] to identify results as matrices of constants, one different letter of the alphabet for each term. And while may not need to have drilled down to the matrix entry level in [math]\displaystyle{ M }[/math], [math]\displaystyle{ \mathrm{T} }[/math], or [math]\displaystyle{ W }[/math], we do at least need to drill down to the entry level of these constant matrices.
So, in the case of our first term, we'll be replacing [math]\displaystyle{ 𝔐𝔐^\mathsf{T} }[/math] with [math]\displaystyle{ \mathrm{A} }[/math]. And if we've set [math]\displaystyle{ r=2 }[/math], then this is a matrix with shape [math]\displaystyle{ (2,2) }[/math], so it'll have entries [math]\displaystyle{ \mathrm{a}_{11} }[/math], [math]\displaystyle{ \mathrm{a}_{12} }[/math], [math]\displaystyle{ \mathrm{a}_{21} }[/math], and [math]\displaystyle{ \mathrm{a}_{22} }[/math]. We've indicated shapes below each matrix in the following:
[math]\displaystyle{
\begin{align}
\frac12
\begin{array} {c}
𝒈 \\
\left[ \begin{array} {r}
g_1 & g_2 \\
\end{array} \right] \\
\small (1,2)
\end{array}
\begin{array} {c}
\mathrm{A} \\
\left[ \begin{array} {r}
\mathrm{a}_{11} & \mathrm{a}_{12} \\
\mathrm{a}_{21} & \mathrm{a}_{22} \\
\end{array} \right] \\
\small (2,2)
\end{array}
\begin{array} {c}
𝒈^\mathsf{T} \\
\left[ \begin{array} {r}
g_1 \\
g_2 \\
\end{array} \right] \\
\small (2,1)
\end{array}
&= \\[12pt]
\frac12
\begin{array} {c}
𝒈 \\
\left[ \begin{array} {r}
g_1 & g_2 \\
\end{array} \right] \\
\small (1,2)
\end{array}
\begin{array} {c}
\mathrm{A}𝒈^\mathsf{T} \\
\left[ \begin{array} {r}
\mathrm{a}_{11}g_1 + \mathrm{a}_{12}g_2 \\
\mathrm{a}_{21}g_1 + \mathrm{a}_{22}g_2 \\
\end{array} \right] \\
\small (2,1)
\end{array}
&= \\[12pt]
\frac12
\begin{array} {c}
𝒈\mathrm{A}𝒈^\mathsf{T} \\
\left[ \begin{array} {r}
(\mathrm{a}_{11}g_1 + \mathrm{a}_{12}g_2)g_1 + (\mathrm{a}_{21}g_1 + \mathrm{a}_{22}g_2)g_2
\end{array} \right] \\
\small (1,1)
\end{array}
&= \\[12pt]
\frac12\mathrm{a}_{11}g_1^2 + \frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_1g_2 + \frac12\mathrm{a}_{22}g_2^2
\end{align}
}[/math]
Yes, there's a reason we haven't pulled the [math]\displaystyle{ \frac12 }[/math] into the constant matrix, despite it clearly being a constant. It's the same reason we deliberately introduced it to our equation out of nowhere earlier. We'll see soon enough.
Now let's work out the second term, [math]\displaystyle{ 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} }[/math]. Again, we should do as little as possible other than breaking down [math]\displaystyle{ 𝒈 }[/math]. So with [math]\displaystyle{ 𝖏 }[/math] a [math]\displaystyle{ (1, k) }[/math]-shaped matrix and [math]\displaystyle{ 𝔐^\mathsf{T} }[/math] a [math]\displaystyle{ (k, r) }[/math]-shaped matrix, those two together are a [math]\displaystyle{ (1, r) }[/math]-shaped matrix, and [math]\displaystyle{ r=2 }[/math] in our example. And that's our [math]\displaystyle{ \mathrm{B} }[/math]. So:
[math]\displaystyle{
\begin{align}
\begin{array} {c}
\mathrm{B} \\
\left[ \begin{array} {r}
\mathrm{b}_{11} & \mathrm{b}_{12} \\
\end{array} \right] \\
\small (1,2)
\end{array}
\begin{array} {c}
𝒈^\mathsf{T} \\
\left[ \begin{array} {r}
g_1 \\
g_2 \\
\end{array} \right] \\
\small (2,1)
\end{array}
&= \\[12pt]
\begin{array} {c}
\mathrm{B}𝒈^\mathsf{T} \\
\left[ \begin{array} {r}
\mathrm{b}_{11}g_1 + \mathrm{b}_{12}g_2 \\
\end{array} \right] \\
\small (1,1)
\end{array}
&= \\[12pt]
\mathrm{b}_{11}g_1 + \mathrm{b}_{12}g_2
\end{align}
}[/math]
Third term to break down: [math]\displaystyle{ \frac12𝖏𝖏^\mathsf{T} }[/math]. This one has neither a [math]\displaystyle{ 𝒈 }[/math] nor a [math]\displaystyle{ \textbf{λ} }[/math] in it, and is a [math]\displaystyle{ (1, 1) }[/math]-shaped matrix, so all we have to do is get it into our constant form: [math]\displaystyle{ \frac12\mathrm{c}_{11} }[/math] (for consistency, leaving the [math]\displaystyle{ \frac12 }[/math] alone, though this one matters less).
Fourth term to break down: [math]\displaystyle{ 𝒈M\mathrm{H}\textbf{λ} }[/math]. Well, [math]\displaystyle{ M\mathrm{H} }[/math] is a [math]\displaystyle{ (r, d)(d, h) = (r, h) }[/math]-shaped matrix, and we know [math]\displaystyle{ r=2 }[/math] and [math]\displaystyle{ h=1 }[/math], so our constant matrix [math]\displaystyle{ \mathrm{D} }[/math] is a [math]\displaystyle{ (2, 1) }[/math]-shaped matrix.
[math]\displaystyle{
\begin{align}
\begin{array} {c}
𝒈 \\
\left[ \begin{array} {r}
g_1 & g_2 \\
\end{array} \right] \\
\small (1, 2)
\end{array}
\begin{array} {c}
\mathrm{D} \\
\left[ \begin{array} {r}
\mathrm{d}_{11} \\
\mathrm{d}_{12} \\
\end{array} \right] \\
\small (2, 1)
\end{array}
\begin{array} {c}
\textbf{λ} \\
\left[ \begin{array} {r}
λ_1 \\
\end{array} \right] \\
\small (1, 1)
\end{array}
&= \\[12pt]
\begin{array} {c}
𝒈\mathrm{D} \\
\left[ \begin{array} {r}
\mathrm{d}_{11}g_1 + \mathrm{d}_{12}g_2
\end{array} \right] \\
\small (1,1)
\end{array}
\begin{array} {c}
\textbf{λ} \\
\left[ \begin{array} {r}
λ_1 \\
\end{array} \right] \\
\small (1, 1)
\end{array}
&= \\[12pt]
\begin{array} {c}
𝒈\mathrm{D}\textbf{λ} \\
\left[ \begin{array} {r}
(\mathrm{d}_{11}g_1 + \mathrm{d}_{12}g_2)λ_1
\end{array} \right] \\
\small (1,1)
\end{array}
&= \\[12pt]
\mathrm{d}_{11}g_1λ_1 + \mathrm{d}_{12}g_2λ_1
\end{align}
}[/math]
Okay, the fifth and final term to break down: [math]\displaystyle{ 𝒋\mathrm{H}\textbf{λ} }[/math]. This one's on the quicker side: we can just rewrite it as [math]\displaystyle{ \mathrm{e}_{11}λ_1 }[/math].
Now we just have to put all five of those rewritten terms back together!
[math]\displaystyle{
\begin{array}
\frac12𝒈𝔐𝔐^\mathsf{T}𝒈^\mathsf{T} & - & 𝖏𝔐^\mathsf{T}𝒈^\mathsf{T} & + & \frac12𝖏𝖏^\mathsf{T} & + & 𝒈M\mathrm{H}\textbf{λ} & - & 𝒋\mathrm{H}\textbf{λ} & = \\
\frac12𝒈\mathrm{A}𝒈^\mathsf{T} & - & \mathrm{B}𝒈^\mathsf{T} & + & \frac12\mathrm{C} & + & 𝒈\mathrm{D}\textbf{λ} & - & \mathrm{E}\textbf{λ} & = \\
\frac12\mathrm{a}_{11}g_1^2 + \frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_1g_2 + \frac12\mathrm{a}_{22}g_2^2 & - & \mathrm{b}_{11}g_1 - \mathrm{b}_{12}g_2 & + & \frac12\mathrm{c}_{11} & + & \mathrm{d}_{11}g_1λ_1 + \mathrm{d}_{12}g_2λ_1 & - & \mathrm{e}_{11}λ_1 &
\end{array}
}[/math]
Now that we've gotten our expression in terms of [math]\displaystyle{ g_1 }[/math], [math]\displaystyle{ g_2 }[/math], and [math]\displaystyle{ λ_1 }[/math], we are ready to take our three different derivatives of this, once with respect to each of those three scalar variables (and finally we can see why we introduced the factor of [math]\displaystyle{ \frac12 }[/math]: so that when the exponents of 2 come down as coefficients, they cancel out; well, that's only a partial answer, we suppose, but suffice it to say that if we hadn't done this, later steps wouldn't match up quite right).
[math]\displaystyle{
\small
\begin{array} {c}
f(𝒈, \textbf{λ}) & = & \frac12\mathrm{a}_{11}g_1^2 & + & \frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_1g_2 & + & \frac12\mathrm{a}_{22}g_2^2 & - & \mathrm{b}_{11}g_1 & - & \mathrm{b}_{12}g_2 & + & \frac12\mathrm{c}_{11} & + & \mathrm{d}_{11}g_1λ_1 & + & \mathrm{d}_{12}g_2λ_1 & - & \mathrm{e}_{11}λ_1 & \\
\dfrac{\partial}{\partial{g_1}}f(𝒈, \textbf{λ}) & = & \mathrm{a}_{11}g_1 & + & \frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_2 & + & 0 & - & \mathrm{b}_{11} & - & 0 & + & 0 & + & \mathrm{d}_{11}λ_1 & + & 0 & - & 0 \\
\dfrac{\partial}{\partial{g_2}}f(𝒈, \textbf{λ}) & = & 0 & + & \frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_1 & + & \mathrm{a}_{22}g_2 & - & 0 & - & \mathrm{b}_{12} & + & 0 & + & 0 & + & \mathrm{d}_{12}λ_1 & - & 0 \\
\dfrac{\partial}{\partial{λ_1}}f(𝒈, \textbf{λ}) & = & 0 & + & 0 & + & 0 & - & 0 & - & 0 & + & 0 & + & \mathrm{d}_{11}g_1 & + & \mathrm{d}_{12}g_2 & - & \mathrm{e}_{11} \\
\end{array}
}[/math]
And so, replacing the derivatives in our system, we find:
[math]\displaystyle{
\begin{align}
\mathrm{a}_{11}g_1 + \frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_2 - \mathrm{b}_{11} + \mathrm{d}_{11}λ_1 &= 0 \\
\frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_1 + \mathrm{a}_{22}g_2 - \mathrm{b}_{12} + \mathrm{d}_{12}λ_1 &= 0 \\
\mathrm{d}_{11}g_1 + \mathrm{d}_{12}g_2 - \mathrm{e}_{11} &= 0 \\
\end{align}
}[/math]
Build matrices back up
In this section we'd like to work our way back from this rather clunky and tedious system of equations situation back to matrices. As our first step, let's space our derivative equations' terms out nicely so we can understand better the relationships between them:
[math]\displaystyle{
\begin{array} {c}
\mathrm{a}_{11}g_1 & + & \frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_2 & + & \mathrm{d}_{11}λ_1 & - & \mathrm{b}_{11} & = & 0 \\
\frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_1 & + & \mathrm{a}_{22}g_2 & + & \mathrm{d}_{12}λ_1 & - & \mathrm{b}_{12} & = & 0\\
\mathrm{d}_{11}g_1 & + & \mathrm{d}_{12}g_2 & & & - & \mathrm{e}_{11} & = & 0\\
\end{array}
}[/math]
Next, notice that all of the terms that contain none of our variables are negative. Let's get all of them to the other side of their respective equations:
[math]\displaystyle{
\begin{array} {c}
\mathrm{a}_{11}g_1 & + & \frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_2 & + & \mathrm{d}_{11}λ_1 & = & \mathrm{b}_{11} \\
\frac12(\mathrm{a}_{12} + \mathrm{a}_{21})g_1 & + & \mathrm{a}_{22}g_2 & + & \mathrm{d}_{12}λ_1 & = & \mathrm{b}_{12} \\
\mathrm{d}_{11}g_1 & + & \mathrm{d}_{12}g_2 & & & = & \mathrm{e}_{11} \\
\end{array}
}[/math]
Notice also that none of our terms contain more than one of our variables anymore. Let's reorganize these terms in a table according to which variable they contain:
| equation | [math]\displaystyle{ g_1 }[/math] | [math]\displaystyle{ g_2 }[/math] | [math]\displaystyle{ λ_1 }[/math] | (no variable, i.e. constants only) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ \mathrm{a}_{11} }[/math] | [math]\displaystyle{ \frac12(\mathrm{a}_{12} + \mathrm{a}_{21}) }[/math] | [math]\displaystyle{ \mathrm{d}_{11} }[/math] | [math]\displaystyle{ \mathrm{b}_{11} }[/math] |
| 2 | [math]\displaystyle{ \frac12(\mathrm{a}_{12} + \mathrm{a}_{21}) }[/math] | [math]\displaystyle{ \mathrm{a}_{22} }[/math] | [math]\displaystyle{ \mathrm{d}_{12} }[/math] | [math]\displaystyle{ \mathrm{b}_{12} }[/math] |
| 3 | [math]\displaystyle{ \mathrm{d}_{11} }[/math] | [math]\displaystyle{ \mathrm{d}_{12} }[/math] | - | [math]\displaystyle{ \mathrm{e}_{11} }[/math] |
This reorganization is the first step to seeing how we can pull ourselves back into matrix form. Notice some patterns here. The constants are all grouped together by which term they came from. This means we can go back to thinking of this system of equations as a single equation of matrices, replacing these chunks with the original constant matrices:
| equation | [math]\displaystyle{ g_1 }[/math] | [math]\displaystyle{ g_2 }[/math] | [math]\displaystyle{ λ_1 }[/math] | (no variable, i.e. constants only) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ \mathrm{A} }[/math] | [math]\displaystyle{ \mathrm{D} }[/math] | [math]\displaystyle{ \mathrm{B}^\mathsf{T} }[/math] | |
| 2 | ||||
| 3 | [math]\displaystyle{ \mathrm{D}^\mathsf{T} }[/math] | - | [math]\displaystyle{ \mathrm{E}^\mathsf{T} }[/math] | |
The replacements for [math]\displaystyle{ \mathrm{B} }[/math] and [math]\displaystyle{ \mathrm{D} }[/math] may seem obvious enough, but you may initially balk at the replacement of [math]\displaystyle{ \mathrm{A} }[/math] here, but there's a reason that works. It's due to the fact that the thing [math]\displaystyle{ \mathrm{A} }[/math] represents is the product of a thing and its own transpose, which means entries mirrored across the main diagonal are equal to each other. So if [math]\displaystyle{ \mathrm{a}_{12} = \mathrm{a}_{21} }[/math], then [math]\displaystyle{ \frac12(\mathrm{a}_{12} + \mathrm{a}_{21}) = \mathrm{a}_{12} = \mathrm{a}_{21} }[/math]. Feel free to check this yourself, or compare with our work-through in the footnote here.[note 9]
Also note that we made [math]\displaystyle{ \mathrm{E} }[/math] transposed; it's hard to tell because it's a [math]\displaystyle{ (1, 1) }[/math]-shaped matrix, but if we did have more than one held-interval, this'd be more apparent.
And so now we can go back to our original variables.
| equation | [math]\displaystyle{ g_1 }[/math] | [math]\displaystyle{ g_2 }[/math] | [math]\displaystyle{ λ_1 }[/math] | (no variable, i.e. constants only) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 𝔐𝔐^\mathsf{T} }[/math] | [math]\displaystyle{ M\mathrm{H} }[/math] | [math]\displaystyle{ (𝖏𝔐^\mathsf{T})^\mathsf{T} }[/math] | |
| 2 | ||||
| 3 | [math]\displaystyle{ (M\mathrm{H})^\mathsf{T} }[/math] | - | [math]\displaystyle{ (𝒋\mathrm{H})^\mathsf{T} }[/math] | |
And if we think about how matrix multiplication works, we can realize that the headings are just a vector containing our variables. And so the rest is just a couple of augmented matrices. We can fill the matrix with zeros where we don't have any constants. And remember, the data entries in the last column of this table are actually on the right side of the equals signs:
[math]\displaystyle{
\left[ \begin{array} {c|c}
\\
\quad 𝔐𝔐^\mathsf{T} \quad & M\mathrm{H} \\
\hline
\quad (M\mathrm{H})^\mathsf{T} \quad & 0 \\
\end{array} \right]
\left[ \begin{array} {c}
g_1 \\
g_2 \\
\hline
λ_1 \\
\end{array} \right]
=
\left[ \begin{array} {c}
\\
(𝖏𝔐^\mathsf{T})^\mathsf{T} \\
\hline
(𝒋\mathrm{H})^\mathsf{T} \\
\end{array} \right]
}[/math]
But we prefer to think of our generators in a row vector, or map. And everything on the right half is transposed. So we can address both of those issues by transposing everything. Remember, when we transpose, we also reverse the order. Conveniently, because the augmented matrix on the left side of the equation is symmetric across its main diagonal, transposing it does not change its value:
[math]\displaystyle{
\left[ \begin{array} {cc|c}
g_1 & g_2 & λ_1 \\
\end{array} \right]
\left[ \begin{array} {c|c}
\\
\quad 𝔐𝔐^\mathsf{T} \quad & M\mathrm{H} \\
\hline
\quad (M\mathrm{H})^\mathsf{T} \quad & 0 \\
\end{array} \right]
=
\left[ \begin{array} {c|c}
\quad 𝖏𝔐^\mathsf{T} \quad & 𝒋\mathrm{H} \\
\end{array} \right]
}[/math]
The big matrix is invertible, so we can multiply both sides by its inverse to move it to the other side, to help us solve for [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math]:
[math]\displaystyle{
\left[ \begin{array} {cc|c}
g_1 & g_2 & λ_1 \\
\end{array} \right]
=
\left[ \begin{array} {c|c}
\quad 𝖏𝔐^\mathsf{T} \quad & 𝒋\mathrm{H} \\
\end{array} \right]
\left[ \begin{array} {c|c}
\\
\quad 𝔐𝔐^\mathsf{T} \quad & M\mathrm{H} \\
\hline
\quad (M\mathrm{H})^\mathsf{T} \quad & 0 \\
\end{array} \right]^{\large -1}
}[/math]
And let's go back from [math]\displaystyle{ 𝖏 }[/math] to [math]\displaystyle{ 𝒋\mathrm{T}W }[/math] and [math]\displaystyle{ 𝔐 }[/math] to [math]\displaystyle{ M\mathrm{T}W }[/math]:
[math]\displaystyle{
\left[ \begin{array} {cc|c}
g_1 & g_2 & λ_1 \\
\end{array} \right]
=
\left[ \begin{array} {c|c}
𝒋\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} & 𝒋\mathrm{H} \\
\end{array} \right]
\left[ \begin{array} {c|c}
\\
M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} & M\mathrm{H} \\
\hline
\quad (M\mathrm{H})^\mathsf{T} \quad & 0 \\
\end{array} \right]^{\large -1}
}[/math]
And extract the [math]\displaystyle{ 𝒋 }[/math] from the right:
[math]\displaystyle{
\left[ \begin{array} {cc|c}
g_1 & g_2 & λ_1 \\
\end{array} \right]
=
𝒋
\left[ \begin{array} {c|c}
\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} & \mathrm{H} \\
\end{array} \right]
\left[ \begin{array} {c|c}
\\
M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} & M\mathrm{H} \\
\hline
\quad (M\mathrm{H})^\mathsf{T} \quad & 0 \\
\end{array} \right]^{\large -1}
}[/math]
At this point you may begin to notice the similarity between this and the pseudoinverse method. We looked at the pseudoinverse as [math]\displaystyle{ G = \mathrm{T}W(M\mathrm{T}W)^{+} = \mathrm{T}W(M\mathrm{T}W)^\mathsf{T}(M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T})^{-1} }[/math], but all we need to do is multiply both sides by [math]\displaystyle{ 𝒋 }[/math] and you get [math]\displaystyle{ 𝒈 = 𝒋\mathrm{T}W(M\mathrm{T}W)^\mathsf{T}(M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T})^{-1} }[/math], which looks almost the same as the above, only without any of the augmentations that are there to account for the held-intervals:
[math]\displaystyle{
\left[ \begin{array} {cc}
g_1 & g_2 \\
\end{array} \right]
=
𝒋
\left[ \begin{array} {c}
\quad \mathrm{T}W(M\mathrm{T}W)^\mathsf{T} \quad \\
\end{array} \right]
\left[ \begin{array} {c}
\quad M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} \quad \\
\end{array} \right]^{-1}
}[/math]
And so, without held-intervals, the generators can be found as the pseudoinverse of [math]\displaystyle{ M\mathrm{T}W }[/math] (left-multiplied by [math]\displaystyle{ \mathrm{T}W }[/math]), with generators, they can be found as almost the same thing, just with some augmentations to the matrices. This augmentation results in an extra value at the end, [math]\displaystyle{ λ_1 }[/math], but we don't need it and can just discard it. Ta da!
Hardcoded example
At this point everything on the right side of this equation is known. Let's actually plug in some numbers to convince ourselves this makes sense. Suppose we go with an unchanged octave, porcupine temperament, the 6-TILT, and unity-weight damage (and of course, optimization power [math]\displaystyle{ 2 }[/math]). Then we have:
[math]\displaystyle{ \small \begin{array} {c} 𝒋 \\ \left[ \begin{array} {c} 1200.000 & 1901.955 & 2786.314 \\ \end{array} \right] \end{array} , \begin{array} {c} \mathrm{H} \\ \left[ \begin{array} {c} 1 \\ 0 \\ 0 \\ \end{array} \right] \end{array} , \begin{array} {c} M \\ \left[ \begin{array} {c} 1 & 2 & 3 \\ 0 & {-3} & {-5} \\ \end{array} \right] \end{array} , \begin{array} {ccc} \mathrm{T} \\ \left[ \begin{array} {r|r|r|r|r|r|r|r} \;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\ 0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\ \end{array} \right] \end{array} , \begin{array} {ccc} W \\ \left[ \begin{array} {c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]
Before we can plug into our formula, we need to compute a few things. Let's start with [math]\displaystyle{ M\mathrm{H} }[/math]:
[math]\displaystyle{
\begin{array} {c}
M \\
\left[ \begin{array} {c}
1 & 2 & 3 \\
0 & {-3} & {-5} \\
\end{array} \right]
\end{array}
\begin{array} {c}
\mathrm{H} \\
\left[ \begin{array} {c}
1 \\
0 \\
0 \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
M\mathrm{H} \\
\left[ \begin{array} {c}
1 \\
0 \\
\end{array} \right]
\end{array}
}[/math]
As for [math]\displaystyle{ \mathrm{T}W }[/math], that's easy, because [math]\displaystyle{ W }[/math]—being a unity-weight matrix—is an identity matrix, so it's equal simply to [math]\displaystyle{ \mathrm{T} }[/math]. But regarding [math]\displaystyle{ M\mathrm{T}W = M\mathrm{T} }[/math], that would be helpful to compute in advance:
[math]\displaystyle{
\begin{array} {c}
M \\
\left[ \begin{array} {c}
1 & 2 & 3 \\
0 & {-3} & {-5} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
M\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & 2 & {1} & \;\;\;0 & 2 & 1 & 1 & \;\;0 \\
0 & {-3} & {-3} & 3 & {-5} & {-2} & {-5} & 2 \\
\end{array} \right]
\end{array}
}[/math]
And so [math]\displaystyle{ M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} }[/math] would be:
[math]\displaystyle{
\begin{array} {ccc}
M\mathrm{T}W \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & 2 & {1} & \;\;\;0 & 2 & 1 & 1 & \;\;0 \\
0 & {-3} & {-3} & 3 & {-5} & {-2} & {-5} & 2 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
(M\mathrm{T}W)^\mathsf{T} \\
\left[ \begin{array} {c}
1 & 0 \\ \hline
2 & {-3} \\ \hline
{1} & {-3} \\ \hline
0 & 3 \\ \hline
2 & {-5} \\ \hline
1 & {-2} \\ \hline
1 & {-5} \\ \hline
0 & 2 \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} \\
\left[ \begin{array} {c}
12 & {-26} \\
{-26} & 85 \\
\end{array} \right]
\end{array}
}[/math]
And finally, [math]\displaystyle{ \mathrm{T}W(M\mathrm{T}W)^\mathsf{T} }[/math]:
[math]\displaystyle{
\begin{array} {ccc}
\mathrm{T}W \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
(M\mathrm{T}W)^\mathsf{T} \\
\left[ \begin{array} {c}
1 & 0 \\ \hline
2 & {-3} \\ \hline
{1} & {-3} \\ \hline
0 & 3 \\ \hline
2 & {-5} \\ \hline
1 & {-2} \\ \hline
1 & {-5} \\ \hline
0 & 2 \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} \\
\left[ \begin{array} {c}
{-4} & 26 \\
2 & {-5} \\
4 & {-14} \\
\end{array} \right]
\end{array}
}[/math]
Now we just have to plug all that into our formula for [math]\displaystyle{ 𝒈 }[/math] (and [math]\displaystyle{ \textbf{λ} }[/math], though again, we don't really care what it comes out to):
[math]\displaystyle{
\left[ \begin{array} {cc|c}
g_1 & g_2 & λ_1 \\
\end{array} \right]
=
𝒋
\left[ \begin{array} {c|c}
\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} & \mathrm{H} \\
\end{array} \right]
\left[ \begin{array} {c|c}
\\
M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} & M\mathrm{H} \\
\hline
\quad (M\mathrm{H})^\mathsf{T} \quad & 0 \\
\end{array} \right]^{\large -1}
}[/math]
So that's:
[math]\displaystyle{
\begin{align}
\left[ \begin{array} {cc|c}
g_1 & g_2 & λ_1 \\
\end{array} \right]
&=
\begin{array} {c}
𝒋 \\
\left[ \begin{array} {c}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {c}
\begin{array} {c|c}
\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} & \mathrm{H} \\
\end{array} \\
\left[ \begin{array} {cc|c}
{-4} & 26 & 1 \\
2 & {-5} & 0 \\
4 & {-14} & 0 \\
\end{array} \right]
\end{array}
\begin{array} {c}
\begin{array} {c|c}
M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} & M\mathrm{H} \\
\hline
\quad (M\mathrm{H})^\mathsf{T} \quad & 0 \\
\end{array} \\
\left[ \begin{array} {cc|c}
12 & {-26} & 1 \\
{-26} & 85 & 0 \\
\hline
1 & 0 & 0 \\
\end{array} \right]^{\large -1}
\end{array}
\\ &=
\left[ \begin{array} {cc|c}
1200.000 & 163.316 & {-4.627} \\
\end{array} \right]
\end{align}
}[/math]
So as expected, our [math]\displaystyle{ λ_1 }[/math] value came out negative, because of our sign-switching earlier. But what we're really interested in are the first two entries of that map, which are [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math]. Our desired [math]\displaystyle{ 𝒈 }[/math] is {1200.000 163.316]. Huzzah!
For comparison's sake, we can repeat this, but without the unchanged octave:
[math]\displaystyle{
\begin{align}
\left[ \begin{array} {c}
g_1 & g_2 \\
\end{array} \right]
&=
\begin{array} {c}
𝒋 \\
\left[ \begin{array} {c}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {c}
\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} \\
\left[ \begin{array} {c}
{-4} & 26 \\
2 & {-5} \\
4 & {-14} \\
\end{array} \right]
\end{array}
\begin{array} {c}
M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T} \\
\left[ \begin{array} {cc|c}
12 & {-26} \\
{-26} & 85 \\
\end{array} \right]^{\large -1}
\end{array}
\\ &=
\left[ \begin{array} {cc|c}
1198.857 & 162.966 \\
\end{array} \right]
\end{align}
}[/math]
And that's all there is to it.[note 10]
For all-interval tuning schemes
So far we've looked at how to use the linear algebra operation called the pseudoinverse to compute miniRMS tunings. We can use a variation of that approach to solve Euclideanized all-interval tuning schemes. So where miniRMS tuning schemes are those with the optimization power [math]\displaystyle{ p }[/math] is equal to [math]\displaystyle{ 2 }[/math], all-interval minimax-ES tuning schemes are those with the dual norm power [math]\displaystyle{ \text{dual}(q) }[/math] equal to [math]\displaystyle{ 2 }[/math].
Setup
The pseudoinverse of a matrix [math]\displaystyle{ A }[/math] is notated as [math]\displaystyle{ A^{+} }[/math], and for convenience, here's its equation again:
[math]\displaystyle{
A^{+} = A^\mathsf{T}(AA^\mathsf{T})^{-1}
}[/math]
For ordinary tunings, we find [math]\displaystyle{ G }[/math] to be:
[math]\displaystyle{
G = \mathrm{T}W(M\mathrm{T}W)^{+} = \mathrm{T}W(M\mathrm{T}W)^\mathsf{T}(M\mathrm{T}W(M\mathrm{T}W)^\mathsf{T})^{-1}
}[/math]
So for all-interval tunings, we simply substitute in our all-interval analogous objects, and find it to be:
[math]\displaystyle{
G = \mathrm{T}_{\text{p}}S_{\text{p}}(M\mathrm{T}_{\text{p}}S_{\text{p}})^{+} = \mathrm{T}_{\text{p}}S_{\text{p}}(M\mathrm{T}_{\text{p}}S_{\text{p}})^\mathsf{T}(M\mathrm{T}_{\text{p}}S_{\text{p}}(M\mathrm{T}_{\text{p}}S_{\text{p}})^\mathsf{T})^{-1}
}[/math]
That's a lot of [math]\displaystyle{ \mathrm{T}_{\text{p}} }[/math], though, and we know those are equal to [math]\displaystyle{ I }[/math], so let's eliminate them:
[math]\displaystyle{
G = S_{\text{p}}(MS_{\text{p}})^{+} = S_{\text{p}}(MS_{\text{p}})^\mathsf{T}(MS_{\text{p}}(MS_{\text{p}})^\mathsf{T})^{-1}
}[/math]
Example
So suppose we want the minimax-ES tuning of meantone temperament, where [math]\displaystyle{ M }[/math] = [⟨1 1 0] ⟨0 1 4]} and [math]\displaystyle{ C_{\text{p}} = L }[/math]. Basically we just need to compute [math]\displaystyle{ MS_{\text{p}} }[/math]:
[math]\displaystyle{
\begin{array}{c}
M \\
\left[ \begin{array} {r}
1 & 1 & 0 \\
0 & 1 & 4 \\
\end{array} \right]
\end{array}
\begin{array}{c}
S_{\text{p}} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 \\
0 & 0 & \frac{1}{\log_2(5)} \\
\end{array} \right]
\end{array}
=
\begin{array}{c}
MS_{\text{p}} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & \frac{1}{\log2{3}} & 0 \\
0 & \frac{1}{\log2{3}} & \frac{4}{\log2{5}} \\
\end{array} \right]
\end{array}
}[/math]
And plug that in a few times, two of them transposed:
[math]\displaystyle{
G =
\begin{array}{c}
S_{\text{p}} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 \\
0 & 0 & \frac{1}{\log_2(5)} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(MS_{\text{p}})^\mathsf{T} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & 0 \\
\frac{1}{\log2{3}} & \frac{1}{\log2{3}} \\
0 & \frac{4}{\log2{5}} \\
\end{array} \right]
\end{array}
\Huge ( \normalsize
\begin{array}{c}
MS_{\text{p}} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & \frac{1}{\log2{3}} & 0 \\
0 & \frac{1}{\log2{3}} & \frac{4}{\log2{5}} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(MS_{\text{p}})^\mathsf{T} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & 0 \\
\frac{1}{\log2{3}} & \frac{1}{\log2{3}} \\
0 & \frac{4}{\log2{5}} \\
\end{array} \right]
\end{array}
\Huge )^{\Large -1} \normalsize
}[/math]
Work that out and you get (at this point we'll convert to decimal form):
[math]\displaystyle{
G =
\left[ \begin{array} {r}
0.740 & {-0.088} \\
0.260 & 0.088\\
{-0.065} & 0.228\\
\end{array} \right]
}[/math]
And when you multiply that by [math]\displaystyle{ 𝒋 }[/math], we get the generator tuning map [math]\displaystyle{ 𝒈 }[/math] for the minimax-ES tuning of meantone, ⟨1201.397 697.049].
With alternative complexities
The following examples all pick up from a shared setup here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Computing all-interval tuning schemes with alternative complexities.
For all complexities used here (well again at least the first several more basic ones), our formula will be:
[math]\displaystyle{
G = S_{\text{p}}(MS_{\text{p}})^{+} = S_{\text{p}}(MS_{\text{p}})^\mathsf{T}(MS_{\text{p}}(MS_{\text{p}})^\mathsf{T})^{-1}
}[/math]
Minimax-E-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Log-product2. Plugging [math]\displaystyle{ L^{-1} }[/math] into our pseudoinverse method for [math]\displaystyle{ S_{\text{p}} }[/math] we find:
[math]\displaystyle{
G = L^{-1}(ML^{-1})^\mathsf{T}(ML^{-1}(ML^{-1})^\mathsf{T})^{-1}
}[/math]
We already have computed [math]\displaystyle{ ML^{-1} }[/math], so plug that in a few times, two of them transposed:
[math]\displaystyle{
G =
\begin{array}{c}
L^{-1} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 \\
0 & 0 & \frac{1}{\log_2(5)} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(ML^{-1})^\mathsf{T} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & 0 \\
\frac{2}{\log_2(3)} & \frac{-3}{\log_2(3)} \\
\frac{3}{\log_2(5)} & \frac{-5}{\log_2(5)} \\
\end{array} \right]
\end{array}
\Huge ( \normalsize
\begin{array}{c}
ML^{-1} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} \\
0 & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(ML^{-1})^\mathsf{T} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & 0 \\
\frac{2}{\log_2(3)} & \frac{-3}{\log_2(3)} \\
\frac{3}{\log_2(5)} & \frac{-5}{\log_2(5)} \\
\end{array} \right]
\end{array}
\Huge )^{\Large -1} \normalsize
}[/math]
Work that out and you get (at this point we'll convert to decimal form):
[math]\displaystyle{
G =
\left[ \begin{array} {r}
0.991 & 0.623 \\
0.044 & {-0.117} \\
{-0.027} & {-0.129}\\
\end{array} \right]
}[/math]
And when you multiply that by [math]\displaystyle{ 𝒋 }[/math], we get the generator tuning map [math]\displaystyle{ 𝒈 }[/math] for the minimax-ES tuning of porcupine, ⟨1199.562 163.891].
This too can be computed easily with the Wolfram Library:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "minimax-ES"]
Out: {1199.562 163.891]
Minimax-E-sofpr-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Sum-of-prime-factors-with-repetition2. Plugging [math]\displaystyle{ \text{diag}(𝒑)^{-1} }[/math] into our pseudoinverse method for [math]\displaystyle{ S_{\text{p}} }[/math] we find:
[math]\displaystyle{
G = \text{diag}(𝒑)^{-1}(M\text{diag}(𝒑)^{-1})^\mathsf{T}(M\text{diag}(𝒑)^{-1}(M\text{diag}(𝒑)^{-1})^\mathsf{T})^{-1}
}[/math]
We already have [math]\displaystyle{ M\text{diag}(𝒑)^{-1} }[/math] computed, so we plug that in a few times, two of them transposed:
[math]\displaystyle{
G =
\begin{array}{c}
\text{diag}(𝒑)^{-1} \\
\left[ \begin{array} {r}
\frac{1}{2} & 0 & 0 \\
0 & \frac{1}{3} & 0 \\
0 & 0 & \frac{1}{5} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(M\text{diag}(𝒑)^{-1})^\mathsf{T} \\
\left[ \begin{array} {r}
\frac{1}{2} & 0 \\
\frac{2}{3} & \frac{-3}{3} \\
\frac{3}{5} & \frac{-5}{5} \\
\end{array} \right]
\end{array}
\Huge ( \normalsize
\begin{array}{c}
M\text{diag}(𝒑)^{-1} \\
\left[ \begin{array} {r}
\frac{1}{2} & \frac{2}{3} & \frac{3}{5} \\
0 & \frac{-3}{3} & \frac{-5}{5} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(M\text{diag}(𝒑)^{-1})^\mathsf{T} \\
\left[ \begin{array} {r}
\frac{1}{2} & 0 \\
\frac{2}{3} & \frac{-3}{3} \\
\frac{3}{5} & \frac{-5}{5} \\
\end{array} \right]
\end{array}
\Huge )^{\Large -1} \normalsize
}[/math]
Work that out and you get :
[math]\displaystyle{
G =
\left[ \begin{array} {r}
\frac{225}{227} & \frac{285}{454} \\
\frac{10}{227} & \frac{-63}{454} \\
\frac{-6}{227} & \frac{-53}{454} \\
\end{array} \right]
}[/math]
And when you multiply that by [math]\displaystyle{ 𝒋 }[/math], we get the generator tuning map [math]\displaystyle{ 𝒈 }[/math] for the minimax-E-sofpr-S tuning of porcupine, ⟨1199.567 164.102].
This too can be computed easily with the Wolfram Library:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "minimax-E-sopfr-S"]
Out: {1199.567 164.102]
Minimax-E-copfr-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Count-of-prime-factors-with-repetition2. Plugging [math]\displaystyle{ I }[/math] into our pseudoinverse method for [math]\displaystyle{ S_{\text{p}} }[/math] we find:
[math]\displaystyle{
G = I(MI)^\mathsf{T}(MI(MI)^\mathsf{T})^{-1} = M^\mathsf{T}(MM^\mathsf{T})^{-1} = M^{+}
}[/math]
That's right: our answer is simply the pseudoinverse of the mapping.
[math]\displaystyle{
G =
\begin{array}{c}
M^\mathsf{T} \\
\left[ \begin{array} {r}
1 & 0 \\
2 & {-3} \\
3 & {-5} \\
\end{array} \right]
\end{array}
\Huge ( \normalsize
\begin{array}{c}
M \\
\left[ \begin{array} {r}
1 & 2 & 3 \\
0 & {-3} & {-5} \\
\end{array} \right]
\end{array}
\begin{array}{c}
M^\mathsf{T} \\
\left[ \begin{array} {r}
1 & 0 \\
2 & {-3} \\
3 & {-5} \\
\end{array} \right]
\end{array}
\Huge )^{\Large -1} \normalsize
}[/math]
Work that out and you get:
[math]\displaystyle{
G =
\left[ \begin{array} {r}
\frac{34}{35} & \frac{3}{5} \\
\frac{1}{7} & 0 \\
\frac{-3}{35} & \frac{-1}{5} \\
\end{array} \right]
}[/math]
And when you multiply that by [math]\displaystyle{ 𝒋 }[/math], we get the generator tuning map [math]\displaystyle{ 𝒈 }[/math] for the minimax-ES tuning of porcupine, ⟨1198.595 162.737].
This too can be computed easily with the Wolfram Library:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "minimax-E-copfr-S"]
Out: {1198.595 162.737]
Minimax-E-lils-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Log-integer-limit-squared2.
As for the minimax-E-lils-S tuning, we use the pseudoinverse method, but with the same augmented matrices as discussed for the minimax-lils-S tuning discussed later in this article. Well, we've established our [math]\displaystyle{ MS_{\text{p}} }[/math] equivalent, but we still need an equivalent for [math]\displaystyle{ S_{\text{p}} }[/math] alone. This is [math]\displaystyle{ L^{-1} }[/math], but with an extra 1 before the logs of primes are diagonalized:
[math]\displaystyle{
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}} \\
\left[ \begin{array} {ccc|c}
\frac{1}{\log_2(2)} & 0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
}[/math]
So plugging in to
[math]\displaystyle{
G = S_{\text{p}}(MS_{\text{p}})^\mathsf{T}(MS_{\text{p}}(MS_{\text{p}})^\mathsf{T})^{-1}
}[/math]
We get:
[math]\displaystyle{
G =
\begin{array}{c}
S_{\text{p}} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & 0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(MS_{\text{p}})^\mathsf{T} \\
\left[ \begin{array} {rr|r}
\frac{1}{\log_2(2)} & 0 & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{2}{\log_2(3)} & \frac{-3}{\log_2(3)} & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{3}{\log_2(5)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{1} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
\end{array}
\Huge ( \normalsize
\begin{array}{c}
MS_{\text{p}} \\
\left[ \begin{array} {r}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(MS_{\text{p}})^\mathsf{T} \\
\left[ \begin{array} {rr|r}
\frac{1}{\log_2(2)} & 0 & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{2}{\log_2(3)} & \frac{-3}{\log_2(3)} & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{3}{\log_2(5)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{1} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
\end{array}
\Huge )^{\Large -1} \normalsize
}[/math]
Work that out and you get (at this point we'll convert to decimal form):
[math]\displaystyle{
G =
\left[ \begin{array} {rr|r}
0.991 & 0.623 & \style{background-color:#FFF200;padding:5px}{0.000} \\
0.044 & {-0.117} & \style{background-color:#FFF200;padding:5px}{-0.002} \\
{-0.027} & {-0.129} & \style{background-color:#FFF200;padding:5px}{0.001} \\
\hline
\style{background-color:#FFF200;padding:5px}{1.000} & \style{background-color:#FFF200;padding:5px}{0.137} & \style{background-color:#FFF200;padding:5px}{-1.000} \\
\end{array} \right]
}[/math]
(Yet again, compare with the result for minimax-ES; same but augmented.)
And when you multiply that by the augmented version of our [math]\displaystyle{ 𝒋 }[/math], we get the generator tuning map [math]\displaystyle{ 𝒈 }[/math] for the minimax-E-lilS tuning of porcupine, ⟨1199.544 163.888 0.018]. Well, that last entry is only the [math]\displaystyle{ g_{\text{augmented}} }[/math] result, which is junk, so we throw that part away.
This too can be computed easily with the Wolfram Library:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "minimax-ES"]
Out: {1199.544 163.888]
Minimax-E-lols-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Log-odd-limit-squared2. We use the pseudoinverse method, with our same [math]\displaystyle{ MS_{\text{p}} }[/math] and [math]\displaystyle{ S_{\text{p}} }[/math] equivalents as from the minimax-E-lils-S examples:
[math]\displaystyle{
\begin{array}{c}
\text{equiv. of} \; MS_{\text{p}} \\
\left[ \begin{array} {rrr|r}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
\end{array}
}[/math]
[math]\displaystyle{
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}} \\
\left[ \begin{array} {ccc|c}
\frac{1}{\log_2(2)} & 0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
}[/math]
And we have our [math]\displaystyle{ \mathrm{U} }[/math] = [1 0 0⟩, being the octave, but it's augmented to [1 0 0⟩, that last entry being its size. So this whole thing is blue on account of having to do with the held-interval augmentation, but its last entry is green because it's also yellow from the lils augmentation:
[math]\displaystyle{
\begin{array} {c}
\mathrm{U} \\
\left[ \begin{array} {c}
\style{background-color:#00AEEF;padding:5px}{1} \\
\style{background-color:#00AEEF;padding:5px}{0} \\
\style{background-color:#00AEEF;padding:5px}{0} \\
\style{background-color:#8DC73E;padding:5px}{1} \\
\end{array} \right]
\end{array}
}[/math]
And so our [math]\displaystyle{ M\mathrm{U} }[/math] we can think of as our held-interval having been mapped. For this we must ask ourselves "what is [math]\displaystyle{ M }[/math]"? We know what [math]\displaystyle{ MS_{\text{p}} }[/math] is but not really [math]\displaystyle{ M }[/math] itself, i.e. in terms of its augmentation status. So, the present author is not sure, but is going with this: [1 0 0⟩ would normally map to [1 0} in this temperament, and the third entry it needs to fit into the block matrices we're about to build would be mapped by the mapping's junk row, so why not just make it 0. So that gives us:
[math]\displaystyle{
\begin{array} {c}
M\mathrm{U} \\
\left[ \begin{array} {c}
\style{background-color:#00AEEF;padding:5px}{1} \\
\style{background-color:#00AEEF;padding:5px}{0} \\
\style{background-color:#8DC73E;padding:5px}{0} \\
\end{array} \right]
\end{array}
}[/math]
Ah, and [math]\displaystyle{ 𝒋 }[/math] is augmented with a 0 for the lils-stuff that is just junk. Might as well:
[math]\displaystyle{
\begin{array} {c}
𝒋 \\
\left[ \begin{array}
1200 & 1901.955 & 2786.314 & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
}[/math]
Now we need to plug this into the variation on the pseudoinverse formula that accounts for held-intervals:
[math]\displaystyle{
\left[ \begin{array} {cc|c|c}
g_1 & g_2 & \style{background-color:#FFF200;padding:5px}{g_{\text{augmented}}} & \style{background-color:#00AEEF;padding:5px}{λ_1} \\
\end{array} \right]
=
𝒋
\left[ \begin{array} {c|c}
S_{\text{p}}(MS_{\text{p}})^\mathsf{T} & \style{background-color:#00AEEF;padding:5px}{U} \\
\end{array} \right]
\left[ \begin{array} {c|c}
\\
MS_{\text{p}}(MS_{\text{p}})^\mathsf{T} & \style{background-color:#00AEEF;padding:5px}{𝑀U} \\
\hline
\quad \style{background-color:#00AEEF;padding:5px}{(𝑀U)}^\mathsf{T} \quad & \style{background-color:#00AEEF;padding:5px}{0} \\
\end{array} \right]^{\large -1}
}[/math]
So let's just start plugging in!
[math]\displaystyle{
\small
\left[ \begin{array} {cc|c|c}
g_1 & g_2 & \style{background-color:#FFF200;padding:5px}{g_{\text{augmented}}} & \style{background-color:#00AEEF;padding:5px}{λ_1} \\
\end{array} \right]
=
\begin{array} {c}
𝒋 \\
\left[ \begin{array} {c}
1200 & 1901.955 & 2786.314 & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
\left[ \begin{array} {c|c}
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}} \\
\left[ \begin{array} {ccc|c}
\frac{1}{\log_2(2)} & 0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(MS_{\text{p}})^\mathsf{T} \\
\left[ \begin{array} {rr|r}
\frac{1}{\log_2(2)} & 0 & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{2}{\log_2(3)} & \frac{-3}{\log_2(3)} & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{3}{\log_2(5)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{1} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
\end{array}
&
\begin{array}
\mathrm{U} \\
\left[ \begin{array} {c}
\style{background-color:#00AEEF;padding:5px}{1} \\
\style{background-color:#00AEEF;padding:5px}{0} \\
\style{background-color:#00AEEF;padding:5px}{0} \\
\style{background-color:#8DC73E;padding:5px}{1} \\
\end{array} \right]
\end{array}
\\
\end{array} \right]
\left[ \begin{array} {c|c}
\\
\begin{array}{c}
\text{equiv. of} \; MS_{\text{p}} \\
\left[ \begin{array} {rrr|r}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
\end{array}
\begin{array}{c}
(MS_{\text{p}})^\mathsf{T} \\
\left[ \begin{array} {rr|r}
\frac{1}{\log_2(2)} & 0 & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{2}{\log_2(3)} & \frac{-3}{\log_2(3)} & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{3}{\log_2(5)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{1} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
\end{array}
&
\begin{array} {c}
M\mathrm{U} \\
\left[ \begin{array} {c}
\style{background-color:#00AEEF;padding:5px}{1} \\
\style{background-color:#00AEEF;padding:5px}{0} \\
\style{background-color:#8DC73E;padding:5px}{0} \\
\end{array} \right]
\end{array}
\\
\hline
\begin{array}{c}
(M\mathrm{U})^\mathsf{T} \\
\left[ \begin{array} {r}
\style{background-color:#00AEEF;padding:5px}{1} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#8DC73E;padding:5px}{0} \\
\end{array} \right]
\end{array}
& \style{background-color:#00AEEF;padding:5px}{0} \\
\end{array} \right]^{\large -1}
}[/math]
Now if you crunch all that on the right, you get ⟨1200 164.062 -0.211 -0.229]. So we can throw away both the lambda that helped us hold our octave unchanged, and then the augmented generator that helped us account for the size of our intervals. So we're left with our held-octave minimax-E-lils-S tuning.
This too can be computed by the Wolfram Library:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "held-octave minimax-E-lils-S"]
Out: {1200 164.062]
Zero-damage method
The second optimization power we'll take a look at is [math]\displaystyle{ p = 1 }[/math], for miniaverage tuning schemes.
Note that miniaverage tunings have not been advocated by tuning theorists thus far. We've included this section largely in order to complete the set of methods with exact solutions, one for each of the key optimization powers [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], and [math]\displaystyle{ ∞ }[/math].[note 11] So, you may prefer to skip ahead to the next section if you're feeling more practically minded. However, the method for [math]\displaystyle{ p = ∞ }[/math] is related but more complicated, and its explanation builds upon this method's explanation, so it may still be worth it to work through this one first.
The high-level summary here is that we're going to collect every tuning where one target-interval for each generator is tuned pure simultaneously. Then we will check each of those tunings' damages, and choose the tuning of those which causes the least damage.
The zero-damage point set
The method for finding the miniaverage leverages the fact that the sum graph changes slope wherever a target-interval is tuned pure. The minimum must be found among the points where [math]\displaystyle{ r }[/math] target-intervals are all tuned pure at once, where [math]\displaystyle{ r }[/math] is the rank of the temperament. This is because this is the maximum number of linearly independent intervals that could be pure at once, given only [math]\displaystyle{ r }[/math] generators to work with. You can imagine that for any point you could find where only [math]\displaystyle{ r - 1 }[/math] intervals were pure at once, that point would be found on a line along which all [math]\displaystyle{ r - 1 }[/math] of those intervals remain pure, but if you follow it far enough in one direction, you'll reach a point where one additional interval is also pure.
These points taken together are known as the zero-damage point set. This is the first of two methods we'll look at in this article which make use of a point set. The other is the method for finding the minimax, which uses a different point set called the "coinciding-damage point set"; this method is slightly trickier than the miniaverage one, though, and so we'll be looking at it next, right after we've covered the miniaverage method here.
So, in essence, this method works by narrowing the infinite space of tuning possibilities down to a finite set of points to check. We gather these zero-damage points, find the damage (specifically the sum of damages to the target-intervals, AKA the power sum where [math]\displaystyle{ p = 1 }[/math]) at each point, and then choose the one with the minimum damage out of those. And that'll be our miniaverage tuning (unless there's a tie, but more on that later).
Gather and process zero-damage points
Let's practice this method by working through an example. For our target-interval list, we can use our recommended scheme, the truncated integer limit triangle (or "TILT" for short), colorized here so we'll be able to visualize their combinations better in the upcoming step. This is the 6-TILT, our default target list for 5-limit temperaments.
[math]\displaystyle{
\mathrm{T} =
\begin{array} {c}
\ \ \begin{array} {c}
\textbf{i}_1 & \ \ \ \textbf{i}_2 & \ \ \ \textbf{i}_3 & \ \ \ \textbf{i}_4 & \ \ \ \textbf{i}_5 & \ \ \ \textbf{i}_6 & \ \ \ \textbf{i}_7 & \ \ \ \textbf{i}_8 \\
\frac21 & \ \ \ \frac31 & \ \ \ \frac32 & \ \ \ \frac43 & \ \ \ \frac52 & \ \ \ \frac53 & \ \ \ \frac54 & \ \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\style{background-color:#F69289;padding:5px}{1} & \style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} & \style{background-color:#98CC70;padding:5px}{2} & \style{background-color:#3FBC9D;padding:5px}{-1} & \style{background-color:#41B0E4;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{-2} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#FDBC42;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{-1} & \style{background-color:#3FBC9D;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{-1} & \style{background-color:#7977B8;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{1} & \style{background-color:#41B0E4;padding:5px}{1} & \style{background-color:#7977B8;padding:5px}{1} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
}[/math]
And let's use a classic example for our temperament: meantone.
Unchanged-interval bases
We can compute ahead of time how many points we should find in our zero-damage point set, because it's simply the number of combinations of [math]\displaystyle{ r }[/math] of them. With meantone being a rank-2 temperament, that's [math]\displaystyle{ {{8}\choose{2}} = 28 }[/math] points (8 choose 2 is 28).
Each of these 28 points may be represented by an unchanged-interval basis, symbolized as [math]\displaystyle{ \mathrm{U} }[/math]. An unchanged-interval basis is simply a matrix where each column is a prime-count vector representing a different interval that the tuning of this temperament should leave unchanged. So for example, the matrix ⟨[-1 1 0⟩ [0 -1 1⟩] tells us that [math]\displaystyle{ \frac32 }[/math] = [-1 1 0⟩ and [math]\displaystyle{ \frac53 }[/math] = [0 -1 1⟩ are to be left unchanged. (The "basis" part of the name tells us that furthermore every linear combination of these vectors is also left unchanged, such as 2×[-1 1 0⟩ + -1×[0 -1 1⟩ = [-2 3 -1⟩, AKA [math]\displaystyle{ \frac{27}{20} }[/math]. It also technically tells us that none of the vectors is already a linear combination of the others, i.e. that it is full-column-rank; this may not be true of all of these matrices we're assembling using this automatic procedure, but that's okay because any of these that aren't truly bases will be eliminated for that reason in the next step.)
Note that this unchanged-interval basis [math]\displaystyle{ \mathrm{U} }[/math] is different than our held-unchanged-interval basis [math]\displaystyle{ H }[/math]. There are a couple main differences:
- We didn't ask for these unchanged-interval bases [math]\displaystyle{ \mathrm{U} }[/math]; they're just coming up as part of this algorithm.
- These unchanged-interval bases completely specify the tuning. A held-interval basis [math]\displaystyle{ \mathrm{H} }[/math] has shape [math]\displaystyle{ (d, h) }[/math] where [math]\displaystyle{ h \leq r }[/math], but an unchanged-interval basis [math]\displaystyle{ \mathrm{U} }[/math] always has shape [math]\displaystyle{ (d, r) }[/math]. (Remember, [math]\displaystyle{ r }[/math] is the rank of the temperament, or in other words, the count of generators.)
So here's the full list of 28 unchanged-interval bases corresponding to the zero-damage points for any 5-limit rank-2 temperament (meantone or otherwise), given the 6-TILT as its target-interval set. Use the colorization to better understand the nature of these combinations:
[math]\displaystyle{
\begin{array} {c}
\mathrm{U}_{(1,2)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#F69289;padding:5px}{1} & \style{background-color:#FDBC42;padding:5px}{0} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#FDBC42;padding:5px}{1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#FDBC42;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(1,3)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac43 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#F69289;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(1,4)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac43 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#F69289;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{2} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{-1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(1,5)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#F69289;padding:5px}{1} & \style{background-color:#3FBC9D;padding:5px}{-1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{0} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(1,6)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#F69289;padding:5px}{1} & \style{background-color:#41B0E4;padding:5px}{0} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{-1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(1,7)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#F69289;padding:5px}{1} & \style{background-color:#7977B8;padding:5px}{-2} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{0} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(1,8)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#F69289;padding:5px}{1} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#F69289;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
,
}[/math]
[math]\displaystyle{
\begin{array} {c}
\mathrm{U}_{(2,3)} \\
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac32 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\style{background-color:#FDBC42;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} \\
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(2,4)} \\
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac43 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{2} \\
\style{background-color:#FDBC42;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{-1} \\
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(2,5)} \\
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{-1} \\
\style{background-color:#FDBC42;padding:5px}{1} & \style{background-color:#3FBC9D;padding:5px}{0} \\
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(2,6)} \\
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{0} \\
\style{background-color:#FDBC42;padding:5px}{1} & \style{background-color:#41B0E4;padding:5px}{-1} \\
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(2,7)} \\
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{-2} \\
\style{background-color:#FDBC42;padding:5px}{1} & \style{background-color:#7977B8;padding:5px}{0} \\
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(2,8)} \\
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#FDBC42;padding:5px}{1} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#FDBC42;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
,
}[/math]
[math]\displaystyle{
\begin{array} {c}
\mathrm{U}_{(3,4)} \\
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac43 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FFF200;padding:5px}{-1} & \style{background-color:#98CC70;padding:5px}{2} \\
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{-1} \\
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(3,5)} \\
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FFF200;padding:5px}{-1} & \style{background-color:#3FBC9D;padding:5px}{-1} \\
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#3FBC9D;padding:5px}{0} \\
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(3,6)} \\
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FFF200;padding:5px}{-1} & \style{background-color:#41B0E4;padding:5px}{0} \\
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#41B0E4;padding:5px}{-1} \\
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(3,7)} \\
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FFF200;padding:5px}{-1} & \style{background-color:#7977B8;padding:5px}{-2} \\
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#7977B8;padding:5px}{0} \\
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(3,8)} \\
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#FFF200;padding:5px}{-1} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
,
}[/math]
[math]\displaystyle{
\begin{array} {c}
\mathrm{U}_{(4,5)} \\
\ \ \begin{array} {rrr}
\frac43 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#98CC70;padding:5px}{2} & \style{background-color:#3FBC9D;padding:5px}{-1} \\
\style{background-color:#98CC70;padding:5px}{-1} & \style{background-color:#3FBC9D;padding:5px}{0} \\
\style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(4,6)} \\
\ \ \begin{array} {rrr}
\frac43 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#98CC70;padding:5px}{2} & \style{background-color:#41B0E4;padding:5px}{0} \\
\style{background-color:#98CC70;padding:5px}{-1} & \style{background-color:#41B0E4;padding:5px}{-1} \\
\style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(4,7)} \\
\ \ \begin{array} {rrr}
\frac43 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#98CC70;padding:5px}{2} & \style{background-color:#7977B8;padding:5px}{-2} \\
\style{background-color:#98CC70;padding:5px}{-1} & \style{background-color:#7977B8;padding:5px}{0} \\
\style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(4,8)} \\
\ \ \begin{array} {rrr}
\frac43 & \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#98CC70;padding:5px}{2} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#98CC70;padding:5px}{-1} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
,
}[/math]
[math]\displaystyle{
\begin{array} {c}
\mathrm{U}_{(5,6)} \\
\ \ \begin{array} {rrr}
\frac52 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#3FBC9D;padding:5px}{-1} & \style{background-color:#41B0E4;padding:5px}{0} \\
\style{background-color:#3FBC9D;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{-1} \\
\style{background-color:#3FBC9D;padding:5px}{1} & \style{background-color:#41B0E4;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(5,7)} \\
\ \ \begin{array} {rrr}
\frac52 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#3FBC9D;padding:5px}{-1} & \style{background-color:#7977B8;padding:5px}{-2} \\
\style{background-color:#3FBC9D;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{0} \\
\style{background-color:#3FBC9D;padding:5px}{1} & \style{background-color:#7977B8;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(5,8)} \\
\ \ \begin{array} {rrr}
\frac52 & \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#3FBC9D;padding:5px}{-1} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#3FBC9D;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#3FBC9D;padding:5px}{1} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
,
}[/math]
[math]\displaystyle{
\begin{array} {c}
\mathrm{U}_{(6,7)} \\
\ \ \begin{array} {rrr}
\frac53 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#41B0E4;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{-2} \\
\style{background-color:#41B0E4;padding:5px}{-1} & \style{background-color:#7977B8;padding:5px}{0} \\
\style{background-color:#41B0E4;padding:5px}{1} & \style{background-color:#7977B8;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(6,8)} \\
\ \ \begin{array} {rrr}
\frac53 & \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#41B0E4;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#41B0E4;padding:5px}{-1} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#41B0E4;padding:5px}{1} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
,
}[/math]
[math]\displaystyle{
\begin{array} {c}
\mathrm{U}_{(7,8)} \\
\ \ \begin{array} {rrr}
\frac54 & \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#7977B8;padding:5px}{-2} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#7977B8;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#7977B8;padding:5px}{1} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
}[/math]
Canonicalize and filter deficient matrices
But many of these unchanged-interval bases are actually redundant with each other, by which we mean that they correspond to the same tuning. Said another way, some of these unchanged-interval bases are different bases for the same set of unchanged-intervals.
In order to identify such redundancies, we will put all of our unchanged-interval bases into their canonical form, following the canonicalization process that has already been described for comma bases, because they are bases, tall matrices (have more rows than columns), and their columns represent intervals. Putting matrices into canonical form is a way to determine if, for some definition of "same", they represent the same information. So here's what they look like in that form (no more color here on out; the point about combinations has been made):
[math]\displaystyle{
\scriptsize
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & {-1} \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & {-1} \\
0 & 1 \\
\end{array} \right]
\end{array}
, \\[35pt] \scriptsize
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & 0 \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
, \\[35pt] \scriptsize
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-1} & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-1} & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-1} & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-1} & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac34 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-2} & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac34 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-2} & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac34 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-2} & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
, \\[35pt] \scriptsize
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac34 & \ \ \frac58 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-2} & {-3} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-1} & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac34 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-2} & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & {-1} \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-1} & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
}[/math]
Note, for example, that our matrix representing [math]\displaystyle{ \frac32 }[/math] and [math]\displaystyle{ \frac43 }[/math] (the 14th one here) has been simplified to a matrix representing [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math]; this is as if to say: why define the problem as tuning [math]\displaystyle{ \frac32 }[/math] and [math]\displaystyle{ \frac43 }[/math] pure, when there's only two total different prime factors between these two intervals, so we may as well just use our two generators to make both of those basis primes pure. In fact, any combination of intervals that includes no prime 5 here will have been simplified to this same unchanged-interval basis.
Also note that many intervals are now subunison (less than [math]\displaystyle{ \frac11 }[/math], with a denominator greater than the numerator; for example [math]\displaystyle{ \frac34 }[/math]). While this may be unnatural for musicians to think about, it's just the way the canonicalization math works out, and is irrelevant to tuning, because any damage to an interval will be the same as to its reciprocal.
In some cases at this point, we would eliminate some unchanged-interval bases, those that through the process of canonicalization were simplified to fewer than [math]\displaystyle{ r }[/math] intervals, i.e. they lost a column (or more than one column). In this example, that has not occurred to any of our matrices; in order for it to have occurred, our target-interval set would have needed to include linearly dependent intervals. For example, the intervals [math]\displaystyle{ \frac32 }[/math] and [math]\displaystyle{ \frac94 }[/math] are linearly dependent, and we see these in the 10-TILT that's the default for a 7-limit temperament. So in that case, the unchanged-interval bases that result from the combination of those pairs of intervals will be eliminated. This captures the fact that if you were to purely tune the interval which the others are multiples of, all the others will also be purely tuned, so this is not truly a combination of distinct intervals to purely tune.
De-dupe
And we also see that our [math]\displaystyle{ \frac32 }[/math] and [math]\displaystyle{ \frac65 }[/math] matrix has been changed to [math]\displaystyle{ \frac32 }[/math] and [math]\displaystyle{ \frac54 }[/math]. This may be less obvious in terms of it being a simplification, but it does illuminate how tuning [math]\displaystyle{ \frac32 }[/math] and [math]\displaystyle{ \frac65 }[/math] pure is no different than tuning [math]\displaystyle{ \frac32 }[/math] and [math]\displaystyle{ \frac54 }[/math] pure.
And so now it's time to actually eliminate those redundancies!
[math]\displaystyle{
\scriptsize
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & {-1} \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & 0 \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-1} & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac32 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-1} & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac34 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-2} & {-1} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac34 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-2} & {-2} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac34 & \ \ \frac58 \\
\end{array}
\\
\left[ \begin{array} {r|r}
{-2} & {-3} \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
}[/math]
Counting only 11 matrices still remaining, that means we must have eliminated 17 of them as redundant from our original set of 28.
Convert to generators
Now we just need to convert each of these unchanged-interval bases [math]\displaystyle{ \mathrm{U}_{(i,j)} }[/math] to a corresponding generator embedding [math]\displaystyle{ G }[/math]. To do this, we use the formula [math]\displaystyle{ G = \mathrm{U}(M\mathrm{U})^{-1} }[/math], where [math]\displaystyle{ M }[/math] is the temperament mapping (the derivation of this formula, and examples of working through this calculation, are both described later in this article here: #Only unchanged-intervals method).[note 12]
[math]\displaystyle{
\scriptsize
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{2}{1} & \frac{3}{2} \\
\end{array}
\\
\left[ \begin{array} {rrr}
1 & {-1} \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{2}{1} & \sqrt[4]{5} \\
\end{array}
\\
\left[ \begin{array} {rrr}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \sqrt[3]{\frac{10}{3}} \\
\end{array}
\\
\left[ \begin{array} {rrr}
1 & \frac13 \\
0 & {-\frac13} \\
0 & \frac13 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\sqrt[5]{\frac{162}{5}} & \sqrt[5]{\frac{15}{2}} \\
\end{array}
\\
\left[ \begin{array} {rrr}
\frac15 & {-\frac15} \\
\frac45 & \frac15 \\
{-\frac15} & \frac15 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{3}{\sqrt[4]{5}} & \sqrt[4]{5} \\
\end{array}
\\
\left[ \begin{array} {rrr}
0 & 0 \\
1 & 0 \\
{-\frac14} & \frac14 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\sqrt[6]{\frac{324}{5}} & \sqrt[6]{\frac{45}{4}} \\
\end{array}
\\
\left[ \begin{array} {rrr}
\frac13 & {-\frac13} \\
\frac23 & \frac13 \\
{-\frac16} & \frac16 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{81}{40} & \frac{3}{2} \\
\end{array}
\\
\left[ \begin{array} {rrr}
{-3} & {-1} \\
4 & 1 \\
{-1} & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{9}{2\sqrt[2]{5}} & \frac{3}{2} \\
\end{array}
\\
\left[ \begin{array} {rrr}
{-1} & {-1} \\
2 & 1 \\
{-\frac12} & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\sqrt[3]{\frac{640}{81}} & \sqrt[3]{\frac{10}{3}} \\
\end{array}
\\
\left[ \begin{array} {rrr}
\frac73 & \frac13 \\
{-\frac43} & {-\frac13} \\
\frac13 & \frac13 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{8\sqrt[2]{5}}{9} & \frac{2\sqrt[2]{5}}{3} \\
\end{array}
\\
\left[ \begin{array} {rrr}
3 & 1 \\
{-2} & {-1} \\
\frac12 & \frac12 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{160}{81} & \frac{40}{27} \\
\end{array}
\\
\left[ \begin{array} {rrr}
5 & 3 \\
{-4} & {-3} \\
1 & 1 \\
\end{array} \right]
\end{array}
}[/math]
Note that every one of those unusual looking values above—whether it be [math]\displaystyle{ \frac21 }[/math], [math]\displaystyle{ \frac{81}{40} }[/math], [math]\displaystyle{ \frac{8\sqrt[2]{5}}{9} }[/math], or otherwise in the first column—or [math]\displaystyle{ \frac32 }[/math], [math]\displaystyle{ \frac{40}{27} }[/math], [math]\displaystyle{ \sqrt[3]{\frac{10}{3}} }[/math], or otherwise in the second column—is an approximation of [math]\displaystyle{ \frac21 }[/math] or [math]\displaystyle{ \frac32 }[/math], respectively.
At this point, the only inputs affecting our results have been [math]\displaystyle{ M }[/math] and [math]\displaystyle{ \mathrm{T} }[/math]: [math]\displaystyle{ M }[/math] appears in our formula for [math]\displaystyle{ G }[/math], and our target-interval set [math]\displaystyle{ \mathrm{T} }[/math] was our source of intervals for our set of unchanged-interval bases. Notably [math]\displaystyle{ W }[/math] is missing from that list of inputs affecting our results. So at this point, it doesn't seem to matter what our damage weight slope is (or what the complexity function used for it is, if other than log-product complexity); this list of candidate [math]\displaystyle{ G }[/math]'s is valid in any case of [math]\displaystyle{ W }[/math]. But don't worry; [math]\displaystyle{ W }[/math] will definitely affect the results soon; actually, it comes into play in the next step.
Find damages at points
As the next step, we find the [math]\displaystyle{ 1 }[/math]-sum of the damages to the target-interval set for each of those tunings. We'll work through one example. Let's just grab that third [math]\displaystyle{ G }[/math], then, the one with [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \sqrt[3]{\frac{10}{3}} }[/math].
This is one way to write the formula for the damages of a tuning of a temperament, in weighted cents. You can see the close resemblance to the expression shared earlier in the #Basic algebraic setup section:
[math]\displaystyle{
\textbf{d} = |\,𝒋GM\mathrm{T}W - 𝒋G_{\text{j}}M_{\text{j}}\mathrm{T}W\,|
}[/math]
As discussed in Dave Keenan & Douglas Blumeyer's guide to RTT/Tuning fundamentals#Absolute errors, these vertical bars mean to take the absolute value of each entry of this vector, not to take its magnitude.
As discussed elsewhere, we can simplify this to:
[math]\displaystyle{
\textbf{d} = |\,𝒋(GM - G_{\text{j}}M_{\text{j}})\mathrm{T}W\,|
}[/math]
So here's that. Since we've gone with simplicity-weight damage here, we'll be using [math]\displaystyle{ S }[/math] to represent our simplicity-weight matrix rather than the generic [math]\displaystyle{ W }[/math] for weight matrix:
[math]\displaystyle{
\textbf{d} =
\Huge |
\scriptsize
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
(
\begin{array} {ccc}
G \\
\left[ \begin{array} {rrr}
1 & \frac13 \\
0 & {-\frac13} \\
0 & \frac13 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
1 & 1 & 0 \\
0 & 1 & 4 \\
\end{array} \right]
\end{array}
-
\begin{array} {ccc}
I \\
\left[ \begin{array} {rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array} \right]
\end{array}
)
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
S \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{\log_2(6)} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1}{\log_2(12)} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1}{\log_2(10)} & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(15)} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(20)} & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(30)} \\
\end{array} \right]
\end{array}
\Huge |
}[/math]
Let's start chipping away at this from the left. As our first act, let's consolidate [math]\displaystyle{ 𝒋 }[/math]:
[math]\displaystyle{
\textbf{d} =
\Huge |
\scriptsize
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
(
\begin{array} {ccc}
G \\
\left[ \begin{array} {rrr}
1 & \frac13 \\
0 & {-\frac13} \\
0 & \frac13 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
1 & 1 & 0 \\
0 & 1 & 4 \\
\end{array} \right]
\end{array}
-
\begin{array} {ccc}
I \\
\left[ \begin{array} {rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array} \right]
\end{array}
)
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
S \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{\log_2(6)} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1}{\log_2(12)} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1}{\log_2(10)} & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(15)} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(20)} & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(30)} \\
\end{array} \right]
\end{array}
\Huge |
}[/math]
Distribute the [math]\displaystyle{ 𝒋 }[/math]. We find [math]\displaystyle{ 𝒋GM = 𝒕 }[/math], the tempered-prime tuning map, and [math]\displaystyle{ 𝒋G_{\text{j}}M_{\text{j}} = 𝒋 }[/math], the just-prime tuning map.
[math]\displaystyle{
\textbf{d} =
\Huge |
\scriptsize
(
\begin{array} {ccc}
𝒕 \\
\left[ \begin{array} {rrr}
1200.000 & 1894.786 & 2779.144 \\
\end{array} \right]
\end{array}
-
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
)
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
S \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{\log_2(6)} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1}{\log_2(12)} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1}{\log_2(10)} & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(15)} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(20)} & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(30)} \\
\end{array} \right]
\end{array}
\Huge |
}[/math]
And now we can replace [math]\displaystyle{ 𝒕 - 𝒋 }[/math] with a single variable [math]\displaystyle{ 𝒓 }[/math], which represents the retuning map, which unsurprisingly is just the map which tells us by how much to retune (mistune) each of the primes (this object will come up a lot more when working with all-interval tuning schemes).
[math]\displaystyle{
\textbf{d} =
\Huge |
\scriptsize
\begin{array} {ccc}
𝒓 \\
\left[ \begin{array} {rrr}
0.000 & {-7.169} & {-7.169} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r}
\;\;1 & \;\;\;0 & {-1} & 2 & {-1} & 0 & {-2} & 1 \\
0 & 1 & 1 & {-1} & 0 & {-1} & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & {-1} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
S \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{\log_2(6)} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1}{\log_2(12)} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1}{\log_2(10)} & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(15)} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(20)} & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(30)} \\
\end{array} \right]
\end{array}
\Huge |
}[/math]
And multiplying that by our [math]\displaystyle{ \mathrm{T} }[/math] gives us [math]\displaystyle{ \textbf{e} }[/math], the target-interval error list:
[math]\displaystyle{
\textbf{d} =
\Huge |
\scriptsize
\begin{array} {ccc}
\textbf{e} \\
\left[ \begin{array} {rrr}
0.000 & {-7.169} & {-7.169} & 7.169 & {-7.169} & 0.000 & {-7.169} & 0.000 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
S \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{\log_2(6)} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1}{\log_2(12)} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1}{\log_2(10)} & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(15)} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(20)} & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(30)} \\
\end{array} \right]
\end{array}
\Huge |
}[/math]
Our weights are all positive. The important part is to take the absolute value of the errors. So we can take care of that and get [math]\displaystyle{ |\textbf{e}|S }[/math]:
[math]\displaystyle{
\textbf{d} =
\scriptsize
\begin{array} {ccc}
|\textbf{e}| \\
\left[ \begin{array} {rrr}
|0.000| & |{-7.169}| & |{-7.169}| & |7.169| & |{-7.169}| & |0.000| & |{-7.169}| & |0.000| \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
S \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{\log_2(6)} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1}{\log_2(12)} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1}{\log_2(10)} & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(15)} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(20)} & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{\log_2(30)} \\
\end{array} \right]
\end{array}
}[/math]
And now we multiply that by the weights to get the damages, [math]\displaystyle{ \textbf{d} }[/math].
[math]\displaystyle{
\textbf{d} =
\scriptsize
\left[ \begin{array} {rrr}
0.000 & 4.523 & 2.773 & 2.000 & 2.158 & 0.000 & 1.659 & 0.000 \\
\end{array} \right]
}[/math]
And finally since this tuning scheme is all about the sum of damages, we're actually looking for [math]\displaystyle{ \llzigzag \textbf{d} \rrzigzag _1 }[/math]. So we total these up, and get our final answer: 0.000 + 4.523 + 2.773 + 2.000 + 2.158 + 0.000 + 1.659 + 0.000 = 13.114. And that's in units of simplicity-weighted cents, ¢(S), by the way.
Choose the winner
Now, if we repeat that entire damage calculation process for every one of the eleven tunings we identified as candidates for the miniaverage, then we'd have found the following list of tuning damages: 21.338, 9.444, 13.114, 10.461, 15.658, 10.615, 50.433, 26.527, 25.404, 33.910, and 80.393. So 13.114 isn't bad, but it's apparently not the best we can do. That honor goes to the second tuning there, which has only 9.444 ¢(S) total damage.
Lo and behold, if we cross reference that with our list of [math]\displaystyle{ G }[/math] candidates from earlier, the second one is quarter-comma meantone, the tuning where the fifth is exactly the fourth root of five:
[math]\displaystyle{
G = \left[ \begin{array} {rrr}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
}[/math]
Often people will prefer to have the tuning in terms of the cents sizes of the generators, which is our generator tuning map [math]\displaystyle{ 𝒈 }[/math][note 13], but again we can find that as easily as [math]\displaystyle{ 𝒋G }[/math]:
[math]\displaystyle{
𝒈 =
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
G \\
\left[ \begin{array} {rrr}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
\end{array}
}[/math]
And that works out to ⟨1200.000 696.578].
Tie-breaking
With the 6-TILT miniaverage tuning of meantone (with simplicity-weight damage), we've solved for a unique tuning based on [math]\displaystyle{ G }[/math] that miniaverages the damage to this temperament [math]\displaystyle{ M }[/math].
But sometimes we have a tie between tunings for least average damage, though. For example, if we had we done a unity-weight tuning, in which case [math]\displaystyle{ W = I }[/math], and included the interval [math]\displaystyle{ \frac85 }[/math] in our set, we would have found that quarter-comma meantone tied with another tuning, one with generators of [math]\displaystyle{ \sqrt[5]{\frac{2560}{81}} }[/math] and [math]\displaystyle{ \sqrt[5]{\frac{200}{27}} }[/math], which are approximately 1195.7 ¢ and 693.352 ¢.
In this case, we fall back to our general method, which is equipped to find the true optimum somewhere in between these two extreme ends of goodness, albeit as an approximate solution.[note 14] This method is discussed here: power limit method. Or, if you'd like a refresher on how to think about non-unique tunings, please see Dave Keenan & Douglas Blumeyer's guide to RTT/Tuning fundamentals#Non-unique tunings.
We note that there may be a way to find an exact solution to a nested miniaverage, in a similar fashion to the nested minimax discussed in the coinciding-damage method section below, but it raises some conceptual issues about what a nested miniaverage even means.[note 15] We have done some pondering of this problem but it remains open; we didn't prioritize solving it, on account of the fact that nobody uses miniaverage tunings anyway.
With held-intervals
The zero-damage method is easily modified to handle held-intervals along with target-intervals.[note 16] In short, rather than assembling our set of unchanged-interval bases [math]\displaystyle{ \mathrm{U}_1 }[/math] through [math]\displaystyle{ \mathrm{U}_n }[/math] (where [math]\displaystyle{ n = {{k}\choose{r}} }[/math]) corresponding to the zero-damage points by finding every combination of [math]\displaystyle{ r }[/math] different ones of our [math]\displaystyle{ k }[/math] target-intervals (one for each generator to be responsible for tuning exactly), instead we must first reserve [math]\displaystyle{ h }[/math] (held-unchanged-interval count) columns of each [math]\displaystyle{ \mathrm{U}_n }[/math] for the held-intervals, leaving only the remaining [math]\displaystyle{ r - h }[/math] columns to be assembled from the target-intervals as normal. So, we'll only have [math]\displaystyle{ {{k}\choose{r - h}} }[/math] candidate tunings / zero-damage points / unchanged-interval bases in this case.
In other words, if [math]\displaystyle{ \mathrm{U}_n }[/math] is one of the unchanged-interval bases characterizing a candidate miniaverage tuning, then it must contain [math]\displaystyle{ \mathrm{H} }[/math] itself, the held-interval basis, which does not yet fully characterize our tuning, leaving some wiggle room (otherwise we'd just use the "only held-intervals" approach, discussed later).
For example, if seeking a held-octave miniaverage tuning of a 5-limit, rank-2 temperament with the 6-TILT as our target-interval set, then [math]\displaystyle{ h = 1 }[/math] (only the octave), [math]\displaystyle{ k = 8 }[/math] (there's 8 target-intervals in the 6-TILT), and [math]\displaystyle{ r = 2 }[/math] (meaning of "rank-2"). So we're looking at [math]\displaystyle{ {{k}\choose{r - h}} = {{(8)}\choose{(2) - (1)}} = {{8}\choose{1}} = 8 }[/math] unchanged-interval bases. That's significantly less than the [math]\displaystyle{ {{8}\choose{2}} = 28 }[/math] we had to slog through when [math]\displaystyle{ h = 0 }[/math] in the earlier example, so this will be much faster to compute. All we're doing here, really, is checking each possible tuning where we pair one of our target-intervals with the octave as our unchanged-interval basis.
So, with our unchanged-interval basis (colorized to grey to help visualize its presence in the upcoming steps):
[math]\displaystyle{
\begin{array} {c}
\mathrm{U} \\
\ \ \begin{array} {rrr}
\frac21 \\
\end{array}
\\
\left[ \begin{array} {rrr}
\style{background-color:#D3D3D3;padding:5px}{1} \\
\style{background-color:#D3D3D3;padding:5px}{0} \\
\style{background-color:#D3D3D3;padding:5px}{0} \\
\end{array} \right]
\end{array}
}[/math]
We have the unchanged-interval bases for our zero-damage points:
[math]\displaystyle{
\small
\begin{array} {c}
\mathrm{U}_{(1)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac21 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#D3D3D3;padding:5px}{1} & \style{background-color:#F69289;padding:5px}{1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#F69289;padding:5px}{0} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#F69289;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(2)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#D3D3D3;padding:5px}{1} & \style{background-color:#FDBC42;padding:5px}{0} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#FDBC42;padding:5px}{1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#FDBC42;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(3)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac43 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#D3D3D3;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(4)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac43 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#D3D3D3;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{2} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{-1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(5)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac52 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#D3D3D3;padding:5px}{1} & \style{background-color:#3FBC9D;padding:5px}{-1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{0} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#3FBC9D;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(6)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#D3D3D3;padding:5px}{1} & \style{background-color:#41B0E4;padding:5px}{0} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{-1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#41B0E4;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(7)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac54 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#D3D3D3;padding:5px}{1} & \style{background-color:#7977B8;padding:5px}{-2} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{0} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#7977B8;padding:5px}{1} \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\mathrm{U}_{(8)} \\
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac65 \\
\end{array}
\\
\left[ \begin{array} {r|r}
\style{background-color:#D3D3D3;padding:5px}{1} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{1} \\
\style{background-color:#D3D3D3;padding:5px}{0} & \style{background-color:#D883B7;padding:5px}{-1} \\
\end{array} \right]
\end{array}
}[/math]
(Note that [math]\displaystyle{ \mathrm{U}_{(1)} }[/math] here pairs [math]\displaystyle{ \frac21 }[/math] with [math]\displaystyle{ \frac21 }[/math]. That's because the octave happens to appear both in our held-interval basis [math]\displaystyle{ \mathrm{H} }[/math] and our target-interval list [math]\displaystyle{ \mathrm{T} }[/math]. We could have chosen to remove [math]\displaystyle{ \frac21 }[/math] from [math]\displaystyle{ \mathrm{T} }[/math] upon adding it to [math]\displaystyle{ \mathrm{H} }[/math], because once you're insisting a particular interval takes no damage there's no sense also including it in a list of intervals to minimize damage to. But we chose to leave [math]\displaystyle{ \mathrm{T} }[/math] alone to make our points above more clearly, i.e. with [math]\displaystyle{ k }[/math] remaining equal to [math]\displaystyle{ 8 }[/math].)[note 17]
Now we canonicalize (no need for color anymore; the point has been made about the combinations of target-intervals with held-intervals):
[math]\displaystyle{
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 \\
0 \\
0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & {-1} \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & {-1} \\
0 & 1 \\
\end{array} \right]
\end{array}
}[/math]
Note that [math]\displaystyle{ \mathrm{U}_1 }[/math], the one which had two copies of the octave, has been canonicalized down to a single column, because its vectors are obviously not linearly independent. So it will be filtered out in the next step. Actually, since that's the only eliminated point, let's go ahead and do the next step too, which is deduping; we have a lot of dupes:
[math]\displaystyle{
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac53 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & {-1} \\
0 & 1 \\
\end{array} \right]
\end{array}
}[/math]
Now convert each [math]\displaystyle{ \mathrm{U}_i }[/math] to a [math]\displaystyle{ G_i }[/math]:
[math]\displaystyle{
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{2}{1} & \frac{3}{2} \\
\end{array}
\\
\left[ \begin{array} {rrr}
1 & {-1} \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{2}{1} & \sqrt[4]{5} \\
\end{array}
\\
\left[ \begin{array} {rrr}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \sqrt[3]{\frac{10}{3}} \\
\end{array}
\\
\left[ \begin{array} {rrr}
1 & \frac13 \\
0 & {-\frac13} \\
0 & \frac13 \\
\end{array} \right]
\end{array}
}[/math]
And convert those to generator tuning maps: ⟨1200 701.955], ⟨1200 696.578], and ⟨1200 694.786]. Note that every one of these has a pure-octave period. Then check the damage sums: 353.942 ¢(U), 89.083 ¢(U), and 110.390 ¢(U), respectively. So that tells us that we want the middle result of these three, ⟨1200 696.578], as the minimization of the [math]\displaystyle{ 1 }[/math]-mean of unity-weight damage to the 6-TILT, when we're constrained to the octave being unchanged.
For a rank-3 temperament, with 2 held-intervals, we'd again have 8 choose 1 = 8 tunings to check. With 1 held-interval, we'd have 8 choose 2 = 28 tunings to check.
For all-interval tuning schemes
We can adapt the zero-damage method to compute all-interval tuning schemes where the dual norm power [math]\displaystyle{ \text{dual}(q) }[/math] is equal to [math]\displaystyle{ 1 }[/math]..
Maxization
Per the heading of this section, we might call these "minimax-MS" schemes, where the 'M' here indicates that their interval complexity functions have been "maxized", as opposed to "Euclideanized"; that is, the power and matching root from their norm or summation form has been changed to [math]\displaystyle{ ∞ }[/math] instead of to [math]\displaystyle{ 2 }[/math]. "Maxization" can be thought of as a reference to the fact that distance measured by [math]\displaystyle{ ∞ }[/math]-norms (maxes, remember) resembles distance traveled by "Max the magician" to get from point A to point B; he can teleport through all dimensions except the one he needs to travel furthest in, i.e. the maximum distance he had to go in any one dimension, is the defining distance. (To complete the set, the [math]\displaystyle{ 1 }[/math]-norms could be referred to as "taxicabized", referencing that this is the type of distance a taxicab on a grid of streets would travel… though would these tunings really be "-ized" if this is the logical starting point?)
And to be clear, the [math]\displaystyle{ \textbf{i} }[/math]-norm is maxized here—has norm power [math]\displaystyle{ ∞ }[/math]—because the norm power on the retuning magnitude is [math]\displaystyle{ 1 }[/math], and these norm powers must be duals.
Tuning schemes such as these are not very popular, because where Euclideanizing [math]\displaystyle{ \text{lp-C}() }[/math] already makes tunings less psychoacoustically plausible, maxizing it makes tunings even less plausible.
Example
Let's compute the minimax-MS tuning of meantone temperament. We begin by assembling our list of unchanged-interval bases. This list will be much shorter than it was with ordinary tuning schemes, because the size of this list increases combinatorially with the count of target-intervals, and with only three (proxy) target-intervals here for a 5-limit temperament.
[math]\displaystyle{
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac31 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
1 & 0 \\
0 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac31 & \ \ \frac51 \\
\end{array}
\\
\left[ \begin{array} {r|r}
0 & 0 \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
}[/math]
Neither the canonicalizing, filtering deficient matrices, nor the de-duping steps will have any effect for all-interval tuning computations. Any combination from the set of prime intervals will already be in canonical form, full-column-rank, and distinct from any other combination. Easy peasy.
So now we convert to generators, using the [math]\displaystyle{ G = \mathrm{U}(M\mathrm{U})^{-1} }[/math] trick:
[math]\displaystyle{
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \frac32 \\
\end{array}
\\
\left[ \begin{array} {rrr}
1 & {-1} \\
0 & 1 \\
0 & 0 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac21 & \ \ \sqrt[4]{5} \\
\end{array}
\\
\left[ \begin{array} {rrr}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
\end{array}
,
\begin{array} {c}
\ \ \begin{array} {rrr}
\frac{3}{\sqrt[4]{5}} & \ \ \sqrt[4]{5} \\
\end{array}
\\
\left[ \begin{array} {rrr}
0 & 0 \\
1 & 0 \\
{-\frac14} & \frac14 \\
\end{array} \right]
\end{array}
}[/math]
So these are our candidate generator embeddings. In other words, if we seek to minimize the [math]\displaystyle{ 1 }[/math]-norm of the retuning map for meantone temperament, these are 3 pairs of generators we should check. Though remember we can simplify to checking the [math]\displaystyle{ 1 }[/math]-sum, which is just another way of saying the sum of the retunings. So each of these generator pairs corresponds to a pair of primes being tuned pure, because these are the tunings where the sum of retunings is minimized.
If we want primes 2 and 3 to both be pure, we use generators of [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac32 }[/math] (Pythagorean tuning). If we want primes 2 and 5 to be pure, we use generators of [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \sqrt[4]{5} }[/math] (quarter-comma tuning). If we want primes 3 and 5 to be pure, we use generators [math]\displaystyle{ \frac{3}{\sqrt[4]{5}} ≈ 2.006 }[/math] and [math]\displaystyle{ \sqrt[4]{5} }[/math] (apparently named "quarter-comma 3eantone" tuning).
We note that at the analogous point in the zero-damage method for ordinary tunings, we pointed out that the choice of [math]\displaystyle{ W }[/math] was irrelevant up to this point; similarly, here, the choice of [math]\displaystyle{ S }[/math] has thus far been irrelevant, though it will certainly affect things in the next step.
To decide between these candidates, we check each of them for the magnitude of the error on the primes.
- Pythagorean tuning causes a magnitude of 9.262 ¢/oct of error (all on prime 5).
- Quarter-comma tuning causes a magnitude of 3.393 ¢/oct of error (all on prime 3).
- Quarter-comma 3eantone tuning causes a magnitude of 5.377 ¢/oct of error (all on prime 2).
And so quarter-comma tuning is our winner with the least retuning magnitude. That's the minimax-MS tuning of meantone.
With alternative complexities
No examples will be given here, on account of the lack of popularity of these tunings.
Coinciding-damage method
The third and final specific optimization power we'll take a look at in this article is [math]\displaystyle{ p = ∞ }[/math], for minimax tuning schemes.
The method for minimax tuning schemes is similar to the zero-damage method used for miniaverage tuning schemes, where [math]\displaystyle{ p = 1 }[/math]. However, there are two key differences:
- Instead of gathering only the points created where target-intervals' damage graphs coincide with zero damage, we also gather any points where target-intervals's damage graphs coincide with nonzero damage.
- Where the [math]\displaystyle{ p=1 }[/math] method is not capable of tie-breaking when the basic mini-[math]\displaystyle{ p }[/math]-mean is a range of tunings rather than a single unique optimum tuning, this [math]\displaystyle{ p=∞ }[/math] method is capable of tie-breaking, to find the true single unique optimum tuning.
History
This method was originally developed by Keenan Pepper in 2012,[note 18], in a 142-line long Python file called tiptop.py.
Keenan developed his algorithm specifically for the minimax-S tuning scheme (historically known as "TOP"), the original and quintessential all-interval tuning scheme. The all-interval use case is discussed below in the "For all-interval tuning schemes" section.
Specifically, Keenan's method was developed for its tie-breaking abilities, at a time where the power-limit method's ability to tie-break was unknown or not popular.
Keenan's method was modified in 2021-2023 by Douglas Blumeyer in order to accommodate ordinary tunings—those with target-interval sets where the optimization power is [math]\displaystyle{ ∞ }[/math] and the norm power may be anything or possibly absent—and this is what will be discussed immediately below. Douglas's modifications also included support for held-intervals, and for alternative complexities, both of which are discussed in sections below, and also an improvement that both simplifies it conceptually and allows it to identify optimum tunings more quickly. Dave Keenan further modified Keenan's method during this time so that it can find exact solutions in the form of generator embeddings, which is also reflected in all the explanations below.
The explanation of how this method works is mostly by Douglas Blumeyer, but Dave Keenan and Keenan Pepper himself both helped tremendously with refining it. (Douglas takes credit for any shortcomings, however. In particular, he apologizes: he didn’t have time to make it shorter.)
Coinciding-damage points
Points for finding damage minimaxes
Damage minimaxes are always found at points in tuning damage space where individual target-interval hyper-V damage graphs intersect, or cross, to form a point.
This doesn't mean that every such point will be a damage minimax. It only means that every damage minimax will be such a point.
Now, the reason why a damage minimax point must be a point of intersection of target-interval damage graphs like this is because a minimax can only occur at a point on the max damage graph where it changes slope, and the max damage graph can only change slope where damage graphs cross. In other words, whenever damage graphs cross, then on one side of the crossing, one is on top, while on the other side, the other is on top.
(For the duration of this explanation, we'll be illustrating things in 2D tuning damage space, because it's simplest. We'll wait until the end to generalize these ideas to higher dimensions.)
But many times when damage graphs cross, while this is still true about which target-interval's damage is on top switching, they were all sloping with the same sign, i.e. all up, or all down:
And minimax points will never happen at these sorts of crossings. So we have to be more specific.
A minimax point cannot be just any point where the max damage graph changes slope. It must be at a point where the sign of the slope changes between positive and negative. This will create what we call a "local minimum", the sort of thing that could be our mini-max, or minimum maximum. ("Local minimum" is a technical term, but the "local" part of it turns out not to be relevant to this problem, and it may cause more confusion to attempt to explain why not, so we'll just ignore it.)
We might call this sort of point a [math]\displaystyle{ -+ }[/math] point, in reference to the signs of the slopes to either side. And by analogy, the other kinds would be [math]\displaystyle{ -- }[/math] or [math]\displaystyle{ ++ }[/math] points.
When damage graphs cross while sloping in opposite directions, like this [math]\displaystyle{ -+ }[/math] point, then when we move in either direction away from such a coinciding-damage point, at least one of these target-intervals' damages will be going up. And by the nature of the maximum, all it takes is one of their damages going up in order for their max damage to go up.
And so if we look at it the other way around, it means that from any direction coming in toward this point, the maximum damage is going down, and that once we reach this point, there's nowhere lower to go. That's what we mean by a "minimum."
As for the "local" part of "local minimum", this only means that there might be other minima like this one. In order to deal with that part of the term better, we'll have to start looking not only at two target-intervals' damages at a time, but all of them at once.
When we zoom out and consider all the crossings among all our target-intervals, not just these two, we can see all sorts of different crossings. We have some [math]\displaystyle{ -- }[/math] points and [math]\displaystyle{ ++ }[/math] on the periphery, and some [math]\displaystyle{ -+ }[/math] points in the middle. Notice that we included among those the zero-damage points on the floor, which aren't exactly crossings, per se, but they are closely related, as we'll see soon enough; they sort of make their own local minima all by themselves. (This isn't even all of the crossings, by the way; it's hard to tell, but the slopes of the red and green lines on the left are such that eventually they'll cross, but way, way off the left side of this view.)
Notice that most of the points are [math]\displaystyle{ -+ }[/math] type points (9 of them, including the zero-damage ones). Fewer of them are the mere change-of-slope types, the [math]\displaystyle{ -- }[/math] or [math]\displaystyle{ ++ }[/math] type (5 of them, including the one off-screen to the left). However, of these 9 important [math]\displaystyle{ -+ }[/math] points, only one of them is the actual minimax! In other words, for every other [math]\displaystyle{ -+ }[/math] point, when we consider all the other target-intervals too, we find that at least one of their damage graphs passes above it. The minimax point is the only [math]\displaystyle{ -+ }[/math] that's on top.
So our minimax tuning is found at a point where:
- We have a crossing of target-interval damage graphs,
- But not just any one of those: it has to be a [math]\displaystyle{ -+ }[/math] type crossing,
- But not just any one of those: it has to be the one that's on top.*
Now, it might seem inefficient to check 14 points, the ones that only meet the first bullet's criterion, just to find the one we want that meets all three bullet's criteria. But actually, for a computer, 14 points is easy peasy. If we compared that with how many points it would check while following the general method for solving this, that could be thousands of times more, and it still would only be finding an approximate solution; the general method has a weaker understanding of the nature of the problem it's solving. In fact, this diagram shows a very simple 3-limit temperament with only 4 target-intervals, and the typical case is going to be 7-limit or higher with a dozen or more target-intervals, which gets exponentially more complex. But even then it may still be fewer points for the computer to check overall, even though many of them are not going to work out.
And you might wonder: but why don't we just scan along the max graph and pick the [math]\displaystyle{ -+ }[/math] point? Well, the problem is: we don't have a function for the max damage graph, other than defining it in terms of all the other target-interval damage graphs. So it turns out that checking all of these crossing points is a more efficient way for a computer to find this point, than doing it the way that might seem more obvious to a human observer.
*
Once we start learning about tie-breaking, we'll see that this is not always exactly the case. But it's fine for now.
Points for finding damage miniaverages
In our explanation of the zero-damage method for [math]\displaystyle{ p=1 }[/math], we saw a similar thing in action for damage miniaverages. But these can only be found at a strict subset of such coinciding-damage points. Specifically, a damage miniaverage is found somewhere among the subset of coinciding-damage points wherever a sufficient count of individual target-intervals' hyper-V-shaped damage graphs intersect along the zero-damage floor of the world, in other words, along their creases.
We won't find miniaverages at any of the other coinciding-damage points, at various heights above the zero-damage floor wherever enough hyper-V's intersect to form a point. We do find minimaxes there, because (to review the previous section) in any direction away from such a point, at least one of the damages will be going up, and all it takes is one damage to go up to cause the max damage to go up. But the same fact is not true of average damage.
In 2D we can see plainly that we don't create any local minimum, or even any change of slope, in our average graph at just any crossing of two damage graphs. On one side of their intersection, one is going up and the other is going down. On the other side of their intersection, the same one is still going up and the same other one is still going down! The average is changing at the same rate.
So the only points where we can say for certain that in any direction no intersecting target-interval's damage has anywhere further down to go are the places where enough creases cross to make a point where they're already along the zero-damage floor. So these are the only points worth looking for a damage miniaverage:
Zero-damage coincidings
So: both types of points are coinciding-damage points. In fact, it may be helpful for some readers to think of the zero-damage method and its zero-damage point set as the (coinciding-)zero-damage method and its (coinciding-)zero-damage point set. It simply uses only a specialized subset of coinciding-damage points.
Because both types of points are coinciding-damage points, both types are possible candidates for damage minimax tunings. We can see that zero-damage coincidings are just as valid for getting local minima in the max damage graph:
As we'll see in the next subsection, when intersecting on the zero-damage floor, we actually need one fewer target-interval to create a point. So [math]\displaystyle{ \textbf{i}_2 }[/math] isn't even really necessary here. We just thought it'd be more confusing to leave it off than it would be to keep it in, even though this means we have to accept that the target-intervals are multiples of each other, e.g. we could think of [math]\displaystyle{ \textbf{i}_1 }[/math] and [math]\displaystyle{ \textbf{i}_2 }[/math] here as [math]\displaystyle{ \frac32 }[/math] and [math]\displaystyle{ \frac94 }[/math], respectively, with prime-count vectors [-1 1⟩ and [-2 2⟩, though it's not like that's a problem or anything. In 3D tuning damage space we wouldn't have this multiples problem; there's a lot more natural and arbitrary looking angles that creases can be made to intersect. But in 3D we'd still have the one-fewer-necessary-on-the-floor problem, which is a bigger problem. And in general it's best to demonstrate ideas as simply as possible, so we stuck with 2D.
But this also creates the terminological problem whereby in 2D, a single target-interval damage graph bouncing off the floor is wanted as a "coinciding-damage" point. In this case, we can reassure ourselves by imagining that the unison is always sort of in our target-interval set, and its graph is always the flat plane on the floor, since it can never be damaged. So in a way, the target-interval's damage coincides with the unison, and/or the unison is thought of as the "missing" interval, the one fewer that are required for an intersection here.
We may observe that the latter kind of point, the coinciding-zero-damage points—those where damage graphs intersect on the zero-damage floor—may seem to be less likely candidates for minimax tunings, considering that by the nature of being on the zero-damage floor, where no target-interval's damage could possibly be any lower, there's almost certainly some target-interval with higher damage (whose damage is still increasing in one direction or another). And this can clearly be seen on the diagram we included a bit earlier. However, as we'll find in the later section about tie-breaking, and hinted at in an asterisked comment earlier, these points are often important for tie-breaking between tunings which are otherwise tied with each other when it comes to those higher-up damages (i.e. at least one direction, a higher-up damage is neither going up nor going down, such as along an intersection of two damage graphs whose creases are parallel).
Generalizing to higher dimensions: Counts of target-intervals required to make the points
Another difference between the specific zero-damage points and general coinciding-damage points is that zero-damage points require one fewer target-interval damage graph to intersect in order to produce them. That's because a hyper-V's crease along the zero-damage floor has one fewer dimension than the hyper-V itself.
Perhaps this idea is best understood by explaining separately, for specific familiar dimensions of tuning damage space:
- In 3D tuning damage space, for every hyper-V, the main part of each of its two "wings" is a plane, and we know that it takes two intersecting planes to reduce us to a line, and three intersecting planes to reduce that line further to a single point. But each hyper-V's crease is already a line, so it only takes two intersecting hyper-V creases to reduce us to a point.
- In 2D tuning damage space, each wing of a hyper-V is a line, and it takes two intersecting lines to make a point. But each hyper-V's crease is already a single point, so we don't even need any intersections here to find points of possible minimax interest!
In general, the number of target-intervals whose graphs will intersect at a point—i.e., their damages will coincide—is equal to the dimension of the tuning damage space. So in 3D tuning damage, we need three hyper-V's to intersect. Think of it this way: a 3D point has a coordinate in the format [math]\displaystyle{ (x,y,z) }[/math], and we need one plane, one target-interval, for each element of that coordinate. But for intersections among creases along the floor, we only need one less than the dimensionality of the tuning damage space to specify a point; that's because we already know that one of the coordinates is 0.
The dimension of the tuning damage space will be equal to the count of generators plus one, or in other words, [math]\displaystyle{ r + 1 }[/math], where [math]\displaystyle{ r }[/math] is the rank. This is because tuning damage space has one dimension along the floor for each generator's tuning, and one additional dimension up off the floor for the damage amounts.
Points vs. lines; tuning space vs. tuning damage space
Throughout the discussion of this method, we may sometimes refer to "points" and "tunings" almost interchangeably. We'll attempt to dispel some potential confusion.
In tuning damage space, a tuning corresponds with a vertical line, perpendicular to the zero damage floor. Any point on this line identifies this same tuning. If we took an aerial view on tuning damage space, looking straight down on it—as we do in the topographic, contour style graphs these lines would look like points. Basically in this view, the only dimensions are for the generators, and the extra dimension for damage is collapsed. In other words, we go from tuning damage space back to simply tuning space.
So a 2D tuning damage space collapses to a 1D tuning space: a single line, a continuum of the single generator's size. And a 3D tuning damage space collapses to a 2D tuning space, with one generators' size per axis.
So what's tricky about this method in this regard is that to some extent we care about points in tuning damage space, because it's points where key intersections between tuning damage graphs come up. But when two such points fall on the same vertical line, they've identified the same exact tuning, and are thus redundant. So we should be careful to say these are the same tuning, not the same point, but occasionally it may make sense to call them the same point even if they're offset vertically in tuning damage space, because in tuning space they would be the same point.
It might seem wise to draw the vertical tuning lines that correspond with these points, but in general we've found that this is more noise than it's worth.
How to gather coinciding-damage points
For a general coinciding-damage point
The first step is to iterate over every combination of [math]\displaystyle{ r + 1 }[/math] target-intervals, and for each of those combinations, look at all permutations of their relative directions. The rank [math]\displaystyle{ r }[/math] is the same as generator count in the basic case (later on we'll see how sometimes in this method it's different). And by "direction" we mean in the sense of "undirected value", i.e. are they greater than or less than unison.
Each of these relative direction permutations of target-interval combinations (we can call these "ReDPOTICs", for short) corresponds with a coinciding-damage point, which means a different candidate generator tuning map [math]\displaystyle{ 𝒈 }[/math]. The candidate [math]\displaystyle{ 𝒈 }[/math] which causes the least damage to the target-intervals (according to the [math]\displaystyle{ ∞ }[/math]-mean, i.e. the max statistic) will be elected as our minimax tuning.
Let's look at an example. Suppose our target-intervals are [math]\displaystyle{ \frac32 }[/math], [math]\displaystyle{ \frac54 }[/math], and [math]\displaystyle{ \frac53 }[/math]. And suppose we are working with a rank-1 temperament, i.e. with one generator.
So our combinations of intervals would be: [math]\displaystyle{ \{ \{ \frac32, \frac54 \}, \{ \frac32, \frac53 \} , \{ \frac54, \frac53 \} \} }[/math].
And each of these three combinations has two relative direction permutations: one where both intervals have the same direction, and one where both intervals have different directions. For the first combination, that is, we'd look at both [math]\displaystyle{ \{ \frac32, \frac54 \} }[/math] and at [math]\displaystyle{ \{ \frac32, \frac45 \} }[/math]. As you can see, in the latter case, we've made one of the two intervals subunison (less than [math]\displaystyle{ \frac11 }[/math]). To be clear, we're checking only permutations of relative direction here, by which we mean that there's no need to check the case where both intervals are subunison, or the case where which one of the two intervals is subunison and which one of them stays superunison is swapped.
We can see why we only worry about relative direction by explaining what we're going to do with these permutations of target-interval combinations: find the interval that is their product. The two permutations we've chosen above multiply to [math]\displaystyle{ \frac32 × \frac54 = \frac{15}{8} }[/math] and [math]\displaystyle{ \frac32 × \frac45 = \frac65 }[/math]. Had we chosen the other two permutations, they'd've multiplied to [math]\displaystyle{ \frac23 × \frac45 = \frac{8}{15} }[/math] and [math]\displaystyle{ \frac23 × \frac54 = \frac56 }[/math]. These second two intervals are simply the reciprocals of the first two results, and so in terms of tuning they are equivalent (technically speaking, we only care about undirected intervals, i.e. neither [math]\displaystyle{ \frac{15}{8} }[/math] nor [math]\displaystyle{ \frac{8}{15} }[/math] but rather [math]\displaystyle{ 8:15 }[/math].
As for why we care about the intervals that are the products of these ReDPOTICs, we'll look into that in just a moment. In short, it has to do with our originally stated plan: to find places where target-intervals have coinciding amounts of damage. (If you're feeling bold, you might try to work out how this product could relate to that already; if not, don't worry, we'll eventually explain it all in detail.)
Keenan came up with a clever way to achieve this only-caring-about-relative-direction permutations effect: simply restrict the first element in each combination to the positive direction. This effortlessly eliminates exactly half of the possible permutations, namely, the ones that are reciprocals of all the others. Done.
For a zero-damage point
Gathering the zero-damage points is much more straightforward. We don't need to build a ReDPOTIC. We don't need to worry about ReD (relative direction), or permutations of (PO) anything. We only need to worry about TIC (target-interval combinations).
But remember, these aren't combinations of the same count of target-intervals. They have one less target-interval each. So let's call them "smaller target-interval combinations", or STICs.
For each STIC, then, we simply want each combination of [math]\displaystyle{ r }[/math] of our target-intervals. For our example, with [math]\displaystyle{ r=1 }[/math], that'd simply be [math]\displaystyle{ \{ \{ \frac32 \}, \{ \frac54 \} , \{ \frac53 \} \} }[/math].
How to build constraint matrices
Once we've gathered all of our coinciding-damage points, both the general kind from ReDPOTICs and the zero-damage kind from STICs, we're ready to prepare constraint matrices. When we apply these to our familiar inequalities, we can convert them to solvable equalities. More on that in the next section, where we work through an example.
These constraint matrices are not themselves directly about optimizing tunings; they're simply about identifying tunings that meet these ReDPOTIC and STIC descriptions. Many of these tunings, as we saw in an earlier section, are completely awful! But that's just how it goes. The optimum tuning is among these, but many other tunings technically fit the description we use to find them.
Let's call these matrices [math]\displaystyle{ K }[/math], for "konstraint" ("C" is taken for a more widely important matrix in RTT, the comma basis).
For a general coinciding-damage point
With each of our general coinciding points, we can build a constraint matrix from its ReDPOTIC. Perhaps for some readers the approach could be best summed up near instantaneously by listing what these constraint matrices would be for the example we're going with so far:
[math]\displaystyle{
\begin{array} {c}
\scriptsize 3/2 \\
\scriptsize 5/4 \\
\scriptsize 5/3
\end{array}
\left[ \begin{array} {c}
+1 \\
+1 \\
0
\end{array} \right]
,
\left[ \begin{array} {c}
+1 \\
{-1} \\
0
\end{array} \right]
,
\left[ \begin{array} {c}
+1 \\
0 \\
+1
\end{array} \right]
,
\left[ \begin{array} {c}
+1 \\
0 \\
{-1}
\end{array} \right]
,
\left[ \begin{array} {c}
0 \\
+1 \\
+1
\end{array} \right]
,
\left[ \begin{array} {c}
0 \\
+1 \\
{-1}
\end{array} \right]
}[/math]
Each constraint matrix is a [math]\displaystyle{ (k, r) }[/math]-shaped matrix, i.e. with one column for each generator and one row for each target. Every entry in these constraint matrices will have either a [math]\displaystyle{ 0 }[/math], [math]\displaystyle{ +1 }[/math], or [math]\displaystyle{ -1 }[/math].
- If the value is [math]\displaystyle{ 0 }[/math], it means that target-interval is not included in the combination.
- If the value is [math]\displaystyle{ +1 }[/math], we take the target-interval's superunison value.
- If the value is [math]\displaystyle{ -1 }[/math], we take the target-interval's subunison value.
Another way to look at these values is from the perspective of the product that ultimately we make from the combination of target-intervals: these values are the powers to which to raise each target-interval before multiplying a column up. So a power of +1 includes the target-interval as is, a power of -1 reciprocates it, and a power of 0 sends it to unison (so multiplying it in with the rest has no effect).
So, for example, the last constraint matrix here, [0 +1 -1], means that with our example target-interval list [[math]\displaystyle{ \frac32 }[/math], [math]\displaystyle{ \frac54 }[/math], and [math]\displaystyle{ \frac53 }[/math]] we've got a superunison [math]\displaystyle{ \frac54 }[/math] and a subunison [math]\displaystyle{ \frac53 }[/math] (and no [math]\displaystyle{ \frac32 }[/math]), so that's [math]\displaystyle{ \frac54 × \frac35 = \frac34 }[/math], or in other words, [math]\displaystyle{ (\frac32)^{0}(\frac54)^{+1}(\frac53)^{-1} }[/math]. Yes, we're still in suspense about what the purpose of these products is, but we'll address that soon.
Notice that each first nonzero entry in each constraint matrix is [math]\displaystyle{ +1 }[/math], per the previous section's point about effecting relative direction.
For a zero-damage point
For each of our zero-damage points we can build a constraint matrix from its STIC. Here those are:
[math]\displaystyle{
\begin{array} {c}
\scriptsize 3/2 \\
\scriptsize 5/4 \\
\scriptsize 5/3
\end{array}
\left[ \begin{array} {c}
+1 \\
0 \\
0
\end{array} \right]
,
\left[ \begin{array} {c}
0 \\
+1 \\
0
\end{array} \right]
,
\left[ \begin{array} {c}
0 \\
0 \\
+1
\end{array} \right]
}[/math]
These tell us which interval will be unchanged in the corresponding tuning (take that as a hint for what will happen with the [math]\displaystyle{ K }[/math] for ReDPOTICs!).
Note that since, as we noted earlier, relative direction is irrelevant for zero-damage points, these matrices will never contain -1 entries. They will only ever contain 0 and +1.
A simple example
For our first overarching example, to help us intuit how this technique works, let's use a simplified example where our target-intervals are even simpler than the ones we looked at so far: just the primes, and thus [math]\displaystyle{ \mathrm{T} = \mathrm{T}_{\text{p}} = I }[/math], an identity matrix we can ignore.
Let's also not weight damage so the weight matrix [math]\displaystyle{ W = I }[/math] too.
For our temperament, we'll go with the very familiar 12-ET, so [math]\displaystyle{ M }[/math] = ⟨12 19 28]. Since this mapping is in the 5-prime-limit, our [math]\displaystyle{ 𝒋 }[/math] = 1200 × ⟨[math]\displaystyle{ \log_2(2) }[/math] [math]\displaystyle{ \log_2(3) }[/math] [math]\displaystyle{ \log_2(5) }[/math]]. And since our mapping is an equal temperament, our generator tuning map [math]\displaystyle{ 𝒈 }[/math] has only a single entry [math]\displaystyle{ g_1 }[/math].
A system of approximations
We'll be applying a constraint matrix to our by-now familiar approximation [math]\displaystyle{ 𝒈M \approx 𝒋 }[/math] in order to transform it from an approximation into an equality, that is, to be able to change its approximately equals sign into an equals sign. This is how each of these constraints take us to a single solution.
[math]\displaystyle{
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
g_1 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
12 & 19 & 28 \\
\end{array} \right]
\end{array}
\approx
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200\log_2(2) & 1200\log_2(3) & 1200\log_2(5) \\
\end{array} \right]
\end{array}
}[/math]
Another way to view a matrix expression like this[note 19] is as a system of multiple expressions—in this case, a system of approximations:
[math]\displaystyle{
12g_1 \approx 1200\log_2(2) \\
19g_1 \approx 1200\log_2(3) \\
28g_1 \approx 1200\log_2(5)
}[/math]
One variable to satisfy three approximations… that's asking a lot of that one variable! We can see that if we tried to make these all equalities, it wouldn't be possible for all of them to be true at the same time:
[math]\displaystyle{
12g_1 = 1200\log_2(2) \\
19g_1 = 1200\log_2(3) \\
28g_1 = 1200\log_2(5)
}[/math]
But this of course is the whole idea of tempering: when we approximate some number of primes with fewer generators, we can't approximate all of them exactly at once.
Constraints we apply to the problem, however, can simplify it to a point where there is an actual solution, i.e. where the count of equations matches the count of variables, AKA the count of generators.
Apply constraint to system
So let's try applying one of our constraint matrices to this equation. Suppose we get the constraint matrix [+1 +1 0]. (We may notice this happens to be one of those made from a ReDPOTIC, for a general coinciding-damage point.) This constraint matrix tells us that the target-interval combination is [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math], because those are the target-intervals corresponding to its nonzero entries. And both nonzero entries are [math]\displaystyle{ +1 }[/math] meaning that both target-intervals are combined in the same direction. In other words, [math]\displaystyle{ \frac21 × \frac31 = \frac61 }[/math] is going to have something to do with this (and we're finally about to find out what that is!).
We multiply both sides of our [math]\displaystyle{ 𝒈M \approx 𝒋 }[/math] style setup by that constraint, to produce [math]\displaystyle{ 𝒈MK \approx 𝒋K }[/math]:
[math]\displaystyle{
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
g_1 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
12 & 19 & 28 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
K \\
\left[ \begin{array} {rrr}
+1 \\
+1 \\
0
\end{array} \right]
\end{array}
\approx
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200\log_2(2) & 1200\log_2(3) & 1200\log_2(5) \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
K \\
\left[ \begin{array} {rrr}
+1 \\
+1 \\
0
\end{array} \right]
\end{array}
}[/math]
And now multiply that through, to get:
[math]\displaystyle{
\begin{align}
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
g_1 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
MK \\
\left[ \begin{array} {rrr}
(12)(+1) + (19)(+1) + (28)(0) \\
\end{array} \right]
\end{array}
&\approx
\begin{array} {ccc}
𝒋K \\
\left[ \begin{array} {rrr}
(1200\log_2(2))(+1) + (1200\log_2(3))(+1) + (1200\log_2(5))(0) \\
\end{array} \right]
\end{array}
\\[15pt]
\left[ \begin{array} {rrr}
g_1 \\
\end{array} \right]
\left[ \begin{array} {rrr}
31 \\
\end{array} \right]
&=
\left[ \begin{array} {rrr}
1200\log_2(2) + 1200\log_2(3) \\
\end{array} \right]
\end{align}
}[/math]
So now we've simplified things down to a single equation with a single variable. All of our matrices are [math]\displaystyle{ (1,1) }[/math]-shaped, which is essentially the same thing as a scalar, so we can drop the braces around them and just treat them as such. And we'll swap the [math]\displaystyle{ 31 }[/math] and [math]\displaystyle{ g_1 }[/math] around to put constants and variables in the conventional order, since scalar multiplication is commutative. Finally, we can use a basic logarithmic identity to consolidate what we have on the right-hand side:
[math]\displaystyle{
31g_1 = 1200\log_2(6)
}[/math]
So with our constraint matrix, we've achieved the situation we needed, where we have a matching count of equations and generators. We can solve for this generator tuning:
[math]\displaystyle{
g_1 = \dfrac{1200\log_2(6)}{31}
}[/math]
The meaning of the ReDPOTIC product
And that's our tuning, the tuning found at this coinciding-damage point.
It's a tuning which makes [math]\displaystyle{ \frac61 }[/math] pure by dividing it into 31 equal parts.
In cents, our generator [math]\displaystyle{ g_1 }[/math] is equal to about 100.063 ¢, and indeed 100.063 × 31 = 3101.955, which is exactly [math]\displaystyle{ 1200 × \log_2(6) }[/math].
And so that's what the constraint matrix's ReDPOTIC product [math]\displaystyle{ \frac61 }[/math] had to do with things: this product is an unchanged-interval of this tuning (the only one, in fact).
But our original intention here was to find the tuning where [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math] have coinciding damage. Well, it turns out this is an equivalent situation. If—according to this temperament's mapping ⟨12 19 28]—it takes 12 steps to reach [math]\displaystyle{ \frac21 }[/math] and also it takes 19 steps to reach [math]\displaystyle{ \frac31 }[/math], and that it therefore takes 31 steps to reach a [math]\displaystyle{ \frac61 }[/math], and it is also the case that [math]\displaystyle{ \frac61 }[/math] is pure, then that implies that whatever error there is on [math]\displaystyle{ \frac21 }[/math] must be the exact opposite of whatever damage there is on [math]\displaystyle{ \frac31 }[/math], since their errors apparently cancel out. So if their errors are exact opposites—negations—then their damages are the same. So we achieve coinciding target-interval damages via an unchanged-interval that they all relate to. Cue the success fanfare.
Applying a constraint for a zero-damage point
Let's also try applying a [math]\displaystyle{ K }[/math] for a zero-damage point, i.e. one that came from a STIC.
Suppose we get the constraint matrix [0 0 +1]. This constraint matrix tells us that [math]\displaystyle{ \frac51 }[/math] will be unchanged, because that's the target-interval corresponding to its nonzero entry (all entries of these types of [math]\displaystyle{ K }[/math] will only be 0 or +1, recall).
We multiply both sides of our [math]\displaystyle{ 𝒈M \approx 𝒋 }[/math] style setup by that constraint, to produce [math]\displaystyle{ 𝒈MK \approx 𝒋K }[/math]:
[math]\displaystyle{
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
g_1 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
12 & 19 & 28 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
K \\
\left[ \begin{array} {rrr}
0 \\
0 \\
+1
\end{array} \right]
\end{array}
\approx
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200\log_2(2) & 1200\log_2(3) & 1200\log_2(5) \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
K \\
\left[ \begin{array} {rrr}
0 \\
0 \\
+1
\end{array} \right]
\end{array}
}[/math]
And now multiply that through, to get:
[math]\displaystyle{
\begin{align}
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
g_1 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
MK \\
\left[ \begin{array} {rrr}
(12)(0) + (19)(0) + (28)(+1) \\
\end{array} \right]
\end{array}
&\approx
\begin{array} {ccc}
𝒋K \\
\left[ \begin{array} {rrr}
(1200\log_2(2))(0) + (1200\log_2(3))(0) + (1200\log_2(5))(+1) \\
\end{array} \right]
\end{array}
\\[15pt]
\left[ \begin{array} {rrr}
g_1 \\
\end{array} \right]
\left[ \begin{array} {rrr}
28 \\
\end{array} \right]
&=
\left[ \begin{array} {rrr}
1200\log_2(5) \\
\end{array} \right]
\\[15pt]
28g_1
&=
1200\log_2(5)
\\[15pt]
g_1
&=
\dfrac{1200\log_2(5)}{28}
\\[15pt]
g_1
&=
99.511
\end{align}
}[/math]
Comparing the zero-damage method's unchanged-interval bases with the coinciding-damage method's constraint matrices
If you recall, the zero-damage method for miniaverage tunings works by directly assembling unchanged-interval bases [math]\displaystyle{ \mathrm{U} }[/math] out of combinations of target-intervals. The coinciding-damage method here, however, indirectly achieves unchanged-interval bases via constraint matrices [math]\displaystyle{ K }[/math]. It does this both for the zero-damage points such as are used by the zero-damage method, as well as for the general coinciding-damage points that the zero-damage method does not use.
Though we note that even the general coinciding-damage points, where [math]\displaystyle{ r + 1 }[/math] target-intervals coincide for some possibly nonzero damage, are equivalent to zero-damage points where [math]\displaystyle{ r }[/math] intervals coincide for zero damage; the difference is that these unchanged-intervals are not actually target-intervals, but rather products of pairs of directional permutations of them.
The zero-damage method might have been designed to use constraint matrices, but this would probably be overkill. When general coinciding-damage points are not needed, it's simpler to use unchanged-interval bases directly.
Get damage lists
From here, we basically just need to take every tuning we find from the linear solutions like this, and for each one, find its target-interval damage list, and then from that find its maximum damage.
In an earlier section's example we found a candidate tuning where [math]\displaystyle{ g_1 = \frac{1200\log_2(6)}{31} \approx 100.0632 }[/math], so we could check damages for this one using our familiar formula:
[math]\displaystyle{
\textbf{d} = |\,𝒈M\mathrm{T}W - 𝒋\mathrm{T}W\,|
}[/math]
And we said that both [math]\displaystyle{ \mathrm{T} }[/math] and [math]\displaystyle{ W }[/math] are identity matrices to simplify things so we can get rid of those.
[math]\displaystyle{
\textbf{d} = |\,𝒈M - 𝒋\,|
}[/math]
And now substitute in the 100.0632:
[math]\displaystyle{
\textbf{d} =
\Large |
\normalsize
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
100.0632 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
12 & 19 & 28 \\
\end{array} \right]
\end{array}
-
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 \\
\end{array} \right]
\end{array}
\Large |
}[/math]
Anyway, that's enough busywork for now. You can work that out if you like, and then you'll have to work it out in the same way for every single candidate tuning.
You'll end up with a ton of possible damage lists [math]\displaystyle{ \textbf{d} }[/math], one for each generator tuning [math]\displaystyle{ 𝒈 }[/math] (the [math]\displaystyle{ K }[/math] have been transposed here to fit better):
[math]\displaystyle{
\begin{array} {c}
\left[ \begin{array} {rrr} +1 & +1 & 0 \end{array} \right] & 𝒈_1 = \left[ \begin{array} {rrr} 100.063 \end{array} \right] & \textbf{d}_1 = \left[ \begin{array} {rrr} 0.757 & 0.757 & 15.452 \end{array} \right] \\
\left[ \begin{array} {rrr} +1 & {-1} & 0 \end{array} \right] & 𝒈_2 = \left[ \begin{array} {rrr} 100.279 \end{array} \right] & \textbf{d}_2 = \left[ \begin{array} {rrr} 3.351 & 3.351 & 21.506 \end{array} \right] \\
\left[ \begin{array} {rrr} +1 & 0 & +1 \end{array} \right] & 𝒈_3 = \left[ \begin{array} {rrr} 99.657 \end{array} \right] & \textbf{d}_3 = \left[ \begin{array} {rrr} 4.106 & 8.456 & 4.106 \end{array} \right] \\
\left[ \begin{array} {rrr} +1 & 0 & {-1} \end{array} \right] & 𝒈_4 = \left[ \begin{array} {rrr} 99.144 \end{array} \right] & \textbf{d}_4 = \left[ \begin{array} {rrr} 10.265 & 18.208 & 10.265 \end{array} \right] \\
\left[ \begin{array} {rrr} 0 & +1 & +1 \end{array} \right] & 𝒈_5 = \left[ \begin{array} {rrr} 99.750 \end{array} \right] & \textbf{d}_5 = \left[ \begin{array} {rrr} 2.995 & 6.697 & 6.697 \end{array} \right] \\
\left[ \begin{array} {rrr} 0 & +1 & {-1} \end{array} \right] & 𝒈_6 = \left[ \begin{array} {rrr} 98.262 \end{array} \right] & \textbf{d}_6 = \left[ \begin{array} {rrr} 20.855 & 34.976 & 34.976 \end{array} \right] \\
\left[ \begin{array} {rrr} +1 & 0 & 0 \end{array} \right] & 𝒈_7 = \left[ \begin{array} {rrr} 100.000 \end{array} \right] & \textbf{d}_7 = \left[ \begin{array} {rrr} 0.000 & 1.955 & 13.686\end{array} \right] \\
\left[ \begin{array} {rrr} 0 & +1 & 0 \end{array} \right] & 𝒈_8 = \left[ \begin{array} {rrr} 100.103 \end{array} \right] & \textbf{d}_8 = \left[ \begin{array} {rrr} 1.235 & 0.000 & 16.567 \end{array} \right] \\
\left[ \begin{array} {rrr} 0 & 0 & +1 \end{array} \right] & 𝒈_9 = \left[ \begin{array} {rrr} 99.511 \end{array} \right] & \textbf{d}_9 = \left[ \begin{array} {rrr} 5.866 & 11.242 & 0.000 \end{array} \right] \\
\end{array}
}[/math]
The first six of these are from ReDPOTICs, for general coinciding-damage points. The last three are from STICs, for zero-damage points.
For each damage list, we can find the coinciding damages. In the first tuning, it's the first two target-intervals' damages, both with [math]\displaystyle{ 0.757 }[/math]. In the fifth tuning, it's the second and third target-intervals' damages, both with [math]\displaystyle{ 6.697 }[/math]. Etcetera. Note that these coinciding damages are not necessarily the max damages of the tuning; for example, the third tuning shows the first and third target-intervals both equal to [math]\displaystyle{ 4.106 }[/math] damage, but the second interval has more than twice that, at [math]\displaystyle{ 8.456 }[/math] damage. That's fine. In many cases, in fact, the tuning we ultimately want is one of these where the coinciding damages are not the max damages.
Identify minimax
In order to identify the minimax is generally pretty straightforward. We gather up all the maxes. And pick their min. That's the min-i-max.
So here's the maxes:
[math]\displaystyle{
\begin{array} {c}
𝒈_1 = \left[ \begin{array} {rrr} 100.063 \end{array} \right] & \text{max}(\textbf{d}_1) = 15.452 \\
𝒈_2 = \left[ \begin{array} {rrr} 100.279 \end{array} \right] & \text{max}(\textbf{d}_2) = 21.506 \\
𝒈_3 = \left[ \begin{array} {rrr} 99.657 \end{array} \right] & \text{max}(\textbf{d}_3) = 8.456 \\
𝒈_4 = \left[ \begin{array} {rrr} 99.144 \end{array} \right] & \text{max}(\textbf{d}_4) = 18.208 \\
𝒈_5 = \left[ \begin{array} {rrr} 99.750 \end{array} \right] & \text{max}(\textbf{d}_5) = 6.697 \\
𝒈_6 = \left[ \begin{array} {rrr} 98.262 \end{array} \right] & \text{max}(\textbf{d}_6) = 34.976 \\
𝒈_7 = \left[ \begin{array} {rrr} 100.000 \end{array} \right] & \text{max}(\textbf{d}_7) = 13.686 \\
𝒈_8 = \left[ \begin{array} {rrr} 100.103 \end{array} \right] & \text{max}(\textbf{d}_8) = 16.567 \\
𝒈_9 = \left[ \begin{array} {rrr} 99.511 \end{array} \right] & \text{max}(\textbf{d}_9) = 11.242 \\
\end{array}
}[/math]
Out of these maximum values, 6.697 is the minimum. So that's our minimax tuning, [math]\displaystyle{ 𝒈_5 }[/math], where the generator is 99.750 ¢ and the max damage to any of our target-intervals is 6.697 ¢(U).
Had there been a tie here, i.e. had some other tuning besides [math]\displaystyle{ 𝒈_5 }[/math] also had 6.697 ¢ for its maximum damage, such that more than one tuning tied for minimax, then we would need to move on to tie-breaking. That gets very involved, so we'll look at that in detail in a later section..
A bigger example
The rank-1 temperament case we've just worked through, which has just one generator, was a great introduction, but a bit too simple to demonstrate some of the ideas we want to touch upon here.
- Some aspects of the constraint matrices require multiple generators in order to illustrate effectively.
- And we didn't demonstrate with weighting yet.
- And we didn't demonstrate with a more interesting target-interval set yet.
- And we didn't compute an exact solution via generator embedding yet.
Dang!
So let's work through another example, this time of
- a rank-3 temperament,
- using complexity-weight damage,
- a more interesting target-interval set,
- and get our answer in the form of a generator embedding.
Prepare constraint matrix
If we have three generators, we will have many coinciding-damage points, each one corresponding to its own constraint matrix [math]\displaystyle{ K }[/math]. For this example, we're not going to bother showing all of them. It would be way too much to show. Let's just follow the logic from start to finish with a single constraint matrix.
Let's suppose our target-interval list is [math]\displaystyle{ \{ \frac65, \frac75, \frac85, \frac95, \frac76, \frac43, \frac32, \frac87, \frac97, \frac98 \} }[/math]. We've labeled each of the rows of our [math]\displaystyle{ K }[/math] here with its corresponding target-interval:
[math]\displaystyle{
\begin{array} {rrr}
\scriptsize{6/5} \\
\scriptsize{7/5} \\
\scriptsize{8/5} \\
\scriptsize{9/5} \\
\scriptsize{7/6} \\
\scriptsize{4/3} \\
\scriptsize{3/2} \\
\scriptsize{8/7} \\
\scriptsize{9/7} \\
\scriptsize{9/8} \\
\end{array}
\left[ \begin{array} {rrr}
0 & 0 & 0 \\
+1 & +1 & +1 \\
+1 & 0 & 0 \\
0 & {-1} & 0 \\
0 & 0 & 0 \\
0 & 0 & {-1} \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{array} \right]
}[/math]
As we can see, this is one of the ReDPOTIC types of constraints, for a general coinciding-damage point. (We won't work through a STIC type for this example; there's actually nothing particularly helpful that we don't already understand that would be illustrated by that.)
So this constraint matrix makes three statements:
- The first column tells us that the (possibly-weighted) errors for [math]\displaystyle{ \frac75 }[/math] and [math]\displaystyle{ \frac85 }[/math] are opposites (same value but opposite sign), because the damage to [math]\displaystyle{ \frac75 × \frac85 }[/math] is zero.
- The second column tells us that the (possibly-weighted) errors for [math]\displaystyle{ \frac75 }[/math] and [math]\displaystyle{ \frac95 }[/math] are identical, because the damage to [math]\displaystyle{ \frac75 × \frac59 }[/math] is zero.
- The third column tells us that the (possibly-weighted) errors for [math]\displaystyle{ \frac75 }[/math] and [math]\displaystyle{ \frac43 }[/math] are identical, because the damage to [math]\displaystyle{ \frac75 × \frac34 }[/math] is zero.
Here's something important to observe that we couldn't confront yet with the simpler single-generator example. Note that while there is always one row of the constraint matrix for each generator, each row of the constraint matrix has no particular association with any one of the generators. In other words, it wouldn't make sense for us to label the first column of this [math]\displaystyle{ K }[/math] with [math]\displaystyle{ g_1 }[/math], the second with [math]\displaystyle{ g_2 }[/math], and the third with [math]\displaystyle{ g_3 }[/math] (or any other ordering of those); each column is as relevant to one of those generators as it is to any other. Any one of the generators may turn out to be the one which satisfies one of these constraints. Said another way, when we perform matrix multiplication between this [math]\displaystyle{ K }[/math] matrix and the [math]\displaystyle{ M\mathrm{T}W }[/math] situation, each row of [math]\displaystyle{ K }[/math] touches each row of [math]\displaystyle{ M\mathrm{T}W }[/math], so [math]\displaystyle{ K }[/math]'s influence is exerted across the board.
Another thing to note is that we set up the constraint matrix so that there's one target-interval that has a non-zero entry in each row, and that this is also the first target-interval column with a non-zero entry, i.e. the one that's been anchored to the positive direction. As we can see, in our case, that target-interval is [math]\displaystyle{ \frac75 }[/math]. Setting up our constraint matrix in this way is how we establish—using the transitive property of equality—that all four of these target-intervals with non-zero entries somewhere their column will have coinciding (equal) damages. Because if A's damage equals B's, and B's damage equals C's, then we also know that A's damage equals C's. And same for D. So we end up with A's damage = B's damage = C's damage = D's damage. All four have coinciding damage.
Eventually we want to multiply this constraint matrix by [math]\displaystyle{ M\mathrm{T}W }[/math] and by [math]\displaystyle{ \mathrm{T}W }[/math]. So let's look at those next.
Prepare tempered and just sides of to-be equality
For our mapping, let's use the minimal generator form of breed temperament, and for weights, let's use complexity-weighted damage ([math]\displaystyle{ W = C }[/math]).
[math]\displaystyle{
\scriptsize
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
1 & 1 & 1 & 2 \\
0 & 2 & 3 & 2 \\
0 & 0 & 2 & 1
\end{array} \right]
\end{array}
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r|r}
1 & 0 & 3 & 0 & {-1} & 2 & {-1} & 3 & 0 & {-3} \\
1 & 0 & 0 & 2 & {-1} & {-1} & 1 & 0 & 2 & 2 \\
{-1} & {-1} & {-1} & {-1} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 1 & 0 & 0 & {-1} & {-1} & 0 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
C \\
\text{diag}(\log_2(\left[ \begin{array} {rrr}
30 & 35 & 40 & 45 & 42 & 12 & 6 & 56 & 63 & 72 \\
\end{array} \right]))
\end{array}
}[/math]
And that resolves to the following:
[math]\displaystyle{
\scriptsize
\begin{array} {ccc}
M\mathrm{T}C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r}
\log_2(30) & \log_2(35) & 2\log_2(40) & \log_2(45) & 0 & \log_2(12) & 0 & \log_2(56) & 0 & {-\log_2(72)} \\
{-\log_2(30)} & {-\log_2(35)} & {-3\log_2(40)} & \log_2(45) & 0 & {-2\log_2(12)} & 2\log_2(6) & {-2\log_2(56)} & 2\log_2(63) & 4\log_2(72) \\
{-2\log_2(30)} & {-\log_2(35)} & {-2\log_2(40)} & {-2\log_2(45)} & \log_2(42) & 0 & 0 & {-\log_2(56)} & {-\log_2(63)} & 0 \\
\end{array} \right]
\end{array}
}[/math]
And what we've got on the other side of the equality is [math]\displaystyle{ \mathrm{T}W }[/math]. Note that we're not using [math]\displaystyle{ 𝒋\mathrm{T}W }[/math] here, since we're shooting for a generator embedding [math]\displaystyle{ G }[/math] such that [math]\displaystyle{ G\mathrm{T}W \approx \mathrm{T}W }[/math]; in other words, we took [math]\displaystyle{ 𝒋G\mathrm{T}W \approx 𝒋\mathrm{T}W }[/math] and canceled out the [math]\displaystyle{ 𝒋 }[/math] on both sides.
[math]\displaystyle{
\scriptsize
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r|r}
1 & 0 & 3 & 0 & {-1} & 2 & {-1} & 3 & 0 & {-3} \\
1 & 0 & 0 & 2 & {-1} & {-1} & 1 & 0 & 2 & 2 \\
{-1} & {-1} & {-1} & {-1} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 1 & 0 & 0 & {-1} & {-1} & 0 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
C \\
\text{diag}(\log_2(\left[ \begin{array} {rrr}
30 & 35 & 40 & 45 & 42 & 12 & 6 & 56 & 63 & 72 \\
\end{array} \right]))
\end{array}
}[/math]
And that resolves to the following:
[math]\displaystyle{
\begin{array} {ccc}
\mathrm{T}C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r}
\log_2(30) & 0 & \log_2(40) & 0 & {-\log_2(42)} & 2\log_2(12) & {-\log_2(6)} & 3\log_2(56) & 0 & {-3\log_2(72)} \\
\log_2(30) & 0 & 0 & 2\log_2(45) & {-\log_2(42)} & {-\log_2(12)} & \log_2(6) & 0 & 2\log_2(63) & 2\log_2(72) \\
{-\log_2(30)} & {-\log_2(35)} & {-\log_2(40)} & {-\log_2(45)} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \log_2(35) & 0 & 0 & \log_2(42) & 0 & 0 & {-\log_2(56)} & {-\log_2(63)} & 0 \\
\end{array} \right]
\end{array}
}[/math]
Apply constraint
Now we've got to constrain both sides of the problem. First the left side:
[math]\displaystyle{
\scriptsize
\begin{array} {ccc}
M\mathrm{T}C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r}
\log_2(30) & \log_2(35) & 2\log_2(40) & \log_2(45) & 0 & \log_2(12) & 0 & \log_2(56) & 0 & {-\log_2(72)} \\
{-\log_2(30)} & {-\log_2(35)} & {-3\log_2(40)} & \log_2(45) & 0 & {-2\log_2(12)} & 2\log_2(6) & {-2\log_2(56)} & 2\log_2(63) & 4\log_2(72) \\
{-2\log_2(30)} & {-\log_2(35)} & {-2\log_2(40)} & {-2\log_2(45)} & \log_2(42) & 0 & 0 & {-\log_2(56)} & {-\log_2(63)} & 0 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
K \\
\left[ \begin{array} {rrr}
0 & 0 & 0 \\
+1 & +1 & +1 \\
+1 & 0 & 0 \\
0 & {-1} & 0 \\
0 & 0 & 0 \\
0 & 0 & {-1} \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{array} \right]
\end{array}
→ \\
\begin{array} {c}
M\mathrm{T}CK \\
\left[ \begin{array} {c}
\log_2(35·40^2) & {-\log_2(\frac{45}{35})} & \log_2(\frac{35}{12}) \\
{-\log_2(35·40^3)} & {-\log_2(35·45)} & \log_2(\frac{12^2}{35}) \\
{-\log_2(35·40^2)} & \log_2(\frac{45^2}{35}) & {-\log_2(35)} \\
\end{array} \right]
\end{array}
}[/math]
And now the right side:
[math]\displaystyle{
\scriptsize
\begin{array} {ccc}
\mathrm{T}C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r}
\log_2(30) & 0 & \log_2(40) & 0 & {-\log_2(42)} & 2\log_2(12) & {-\log_2(6)} & 3\log_2(56) & 0 & {-3\log_2(72)} \\
\log_2(30) & 0 & 0 & 2\log_2(45) & {-\log_2(42)} & {-\log_2(12)} & \log_2(6) & 0 & 2\log_2(63) & 2\log_2(72) \\
{-\log_2(30)} & {-\log_2(35)} & {-\log_2(40)} & {-\log_2(45)} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & \log_2(35) & 0 & 0 & \log_2(42) & 0 & 0 & {-\log_2(56)} & {-\log_2(63)} & 0 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
K \\
\left[ \begin{array} {rrr}
0 & 0 & 0 \\
+1 & +1 & +1 \\
+1 & 0 & 0 \\
0 & {-1} & 0 \\
0 & 0 & 0 \\
0 & 0 & {-1} \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{array} \right]
\end{array}
→ \\
\begin{array} {c}
\mathrm{T}CK \\
\left[ \begin{array} {c}
\log_2(40^3) & 0 & {-\log_2(12^2)} \\
0 & {-\log_2(45^2)} & \log_2(12) \\
{-\log_2(35·40)} & \log_2(\frac{45}{35}) & {-\log_2(35)} \\
\log_2(35) & \log_2(35) & \log_2(35) \\
\end{array} \right]
\end{array}
}[/math]
So now we can put them together as an equality, making sure to include the generator embedding that we're solving for on the left-hand side:
[math]\displaystyle{
\small
\begin{array} {c}
G \\
\left[ \begin{array} {c}
g_{11} & g_{12} & g_{13} \\
g_{21} & g_{22} & g_{23} \\
g_{31} & g_{32} & g_{33} \\
g_{41} & g_{42} & g_{43} \\
\end{array} \right]
\end{array}
\begin{array} {c}
M\mathrm{T}CK \\
\left[ \begin{array} {c}
\log_2(35·40^2) & {-\log_2(\frac{45}{35})} & \log_2(\frac{35}{12}) \\
{-\log_2(35·40^3)} & {-\log_2(35·45)} & \log_2(\frac{12^2}{35}) \\
{-\log_2(35·40^2)} & \log_2(\frac{45^2}{35}) & {-\log_2(35)} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\mathrm{T}CK \\
\left[ \begin{array} {c}
\log_2(40^3) & 0 & {-\log_2(12^2)} \\
0 & {-\log_2(45^2)} & \log_2(12) \\
{-\log_2(35·40)} & \log_2(\frac{45}{35}) & {-\log_2(35)} \\
\log_2(35) & \log_2(35) & \log_2(35) \\
\end{array} \right]
\end{array}
}[/math]
Solve for generator embedding
To solve for [math]\displaystyle{ G }[/math], we take the inverse of [math]\displaystyle{ M\mathrm{T}CK }[/math] and right-multiply both sides of the equation by it. This will cancel it out on the left-hand side, isolating [math]\displaystyle{ G }[/math]:
[math]\displaystyle{
\begin{align}
GM\mathrm{T}CK &= \mathrm{T}CK \\
GM\mathrm{T}CK(M\mathrm{T}CK)^{-1} &= \mathrm{T}CK(M\mathrm{T}CK)^{-1} \\
G\cancel{M\mathrm{T}CK}\cancel{(M\mathrm{T}CK)^{-1}} &= \mathrm{T}CK(M\mathrm{T}CK)^{-1} \\
G &= \mathrm{T}CK(M\mathrm{T}CK)^{-1}
\end{align}
}[/math]
And now we just multiply those two things on the right-hand side together:
[math]\displaystyle{
\scriptsize
\begin{array} {c}
\mathrm{T}CK \\
\left[ \begin{array} {c}
\log_2(40^3) & 0 & {-\log_2(12^2)} \\
0 & {-\log_2(45^2)} & \log_2(12) \\
{-\log_2(35·40)} & \log_2(\frac{45}{35}) & {-\log_2(35)} \\
\log_2(35) & \log_2(35) & \log_2(35) \\
\end{array} \right]
\end{array}
\begin{array} {c}
(M\mathrm{T}CK)^{-1} \\
\left[ \begin{array} {c}
3\log_2(35)\log_2(45) - \log_2(12)\log_2(\frac{405}{7}) &
\log_2(35)\log_2(45) - \log_2(12)\log_2(\frac{405}{7}) &
2\log_2(35)\log_2(45) - \log_2(12)\log_2(\frac{18225}{7}) \\
-\log_2(35)\log_2(40) - \log_2(144)\log_2(56000) &
-\log_2(12)\log_2(56000) &
-\log_2(35)\log_2(40) - \log_2(12)\log_2(1400) \\
-8\log_2(40)\log_2(45) - \log_2(35)\log_2(\frac{18225}{8}) &
-\log_2(45)\log_2(56000) &
-\log_2(40)\log_2(45) - \log_2(35)\log_2(\frac{405}{8}) \\
\end{array} \right] \\
\hline
\log_2(\frac98)\log_2(12)\log_2(35) - \log_2(40)\log_2(45)\log_2(\frac{20736}{35})
\end{array}
}[/math]
To find [math]\displaystyle{ G }[/math].
[math]\displaystyle{
\scriptsize
\begin{array} {c}
G \\
\left[ \begin{array} {c}
g_{11} & g_{12} & g_{13} \\
g_{21} & g_{22} & g_{23} \\
g_{31} & g_{32} & g_{33} \\
g_{41} & g_{42} & g_{43} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\mathrm{T}CK(M\mathrm{T}CK)^{-1} \\
\left[ \begin{array} {c}
\begin{array} {c}
9\log_2(35)\log_2(40)\log_2(45) \\
+ 2\log_2(12)\log_2(35)\log_2(\frac{18225}{8}) \\
+ 2\log_2(12)\log_2(40)\log_2(86821875)
\end{array} & &
\begin{array} {c}
3\log_2(35)\log_2(40)\log_2(45) \\
- 3\log_2(12)\log_2(40)\log_2(\frac{405}{7}) \\
+ 2\log_2(12)\log_2(45)\log_2(56000)
\end{array} & &
\begin{array} {c}
6\log_2(35)\log_2(40)\log_2(45) \\
+ 2\log_2(35)\log_2(12)\log_2(\frac{405}{8}) \\
+ \log_2(12)\log_2(40)\log_2(1929375)
\end{array} \\[9pt]
\begin{array} {c}
2\log_2(45)\log_2(35)\log_2(40) \\
+ 3\log_2(45)\log_2(144)\log_2(56000) \\
- 8\log_2(12)\log_2(40)\log_2(45) \\
- \log_2(12)\log_2(35)\log_2(\frac{18225}{8})
\end{array} & &
\begin{array} {c}
\log_2(12)\log_2(45)\log_2(56000)
\end{array} & &
\begin{array} {c}
\log_2(35)\log_2(40)\log_2(45) \\
- 5\log_2(12)\log_2(40)\log_2(45) \\
- \log_2(12)\log_2(35)\log_2(\frac{405}{8}) \\
- 2\log_2(12)\log_2(45)\log_2(1400)
\end{array} \\[9pt]
\begin{array} {c}
\log_2(144)\log_2(40)\log_2(\frac{405}{7}) \\
- \log_2(144)\log_2(45)\log_2(56000) \\
+ 4\log_2(35)\log_2(40)\log_2(45) \\
+ \log_2(35)\log_2(144)\log_2(3240000)
\end{array} & &
\begin{array} {c}
\log_2(12)\log_2(40)\log_2(\frac{405}{7}) \\
- \log_2(12)\log_2(45)\log_2(56000) \\
- \log_2(35)\log_2(40)\log_2(45) \\
+ \log_2(35)\log_2(45)\log_2(56000) \\
+ \log_2(12)\log_2(35)\log_2(3240000) \\
- \log_2(35)\log_2(35)\log_2(45)
\end{array} & &
\begin{array} {c}
\log_2(12)\log_2(40)\log_2(\frac{18225}{7}) \\
+ 2\log_2(35)\log_2(40)\log_2(45) \\
+ \log_2(12)\log_2(35)\log_2(3645000) \\
- \log_2(12)\log_2(45)\log_2(1400)
\end{array} \\[9pt]
\begin{array} {c}
-8\log_2(35)\log_2(40)\log_2(45) \\
-\log_2(35)\log_2(144)\log_2(3240000)
\end{array} & &
\begin{array} {c}
\log_2(35)\log_2(35)\log_2(45) \\
- \log_2(35)\log_2(45)\log_2(5600) \\
- \log_2(12)\log_2(35)\log_2(3240000)
\end{array} & &
\begin{array} {c}
-\log_2(35)\log_2(40)\log_2(45) \\
-\log_2(12)\log_2(35)\log_2(3645000)
\end{array}
\end{array}\right] \\
\hline
\log_2(\frac98)\log_2(12)\log_2(35) - \log_2(40)\log_2(45)\log_2(\frac{20736}{35})
\end{array}
}[/math]
Egads!
Convert generator embedding to generator map
Taking the values from the first column of this, we can find that our first generator, [math]\displaystyle{ \textbf{g}_1 }[/math], is exactly equal to:
[math]\displaystyle{
\small
\sqrt[
\log_2(\frac98)\log_2(12)\log_2(35) - \log_2(40)\log_2(45)\log_2(\frac{20736}{35})
]
{
\rule[15pt]{0pt}{0pt}
2^{(
9\log_2(35)\log_2(40)\log_2(45) + 2\log_2(12)\log_2(35)\log_2(\frac{18225}{8}) + 2\log_2(12)\log_2(40)\log_2(86821875)
)}
}
\hspace{1mu} \overline{\rule[15pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[15pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[15pt]{0pt}{0pt}}
\\
\quad\quad\quad
\overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu}
\overline{\rule[11pt]{0pt}{0pt}
·
3^{(
2\log_2(45)\log_2(35)\log_2(40) + 3\log_2(45)\log_2(144)\log_2(56000) - 8\log_2(12)\log_2(40)\log_2(45) - \log_2(12)\log_2(35)\log_2(\frac{18225}{8})
)}
}
\hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}}
\\
\quad\quad\quad
\overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu}
\overline{\rule[11pt]{0pt}{0pt}
·
5^{(
\log_2(144)\log_2(40)\log_2(\frac{405}{7}) - \log_2(144)\log_2(45)\log_2(56000) + 4\log_2(35)\log_2(40)\log_2(45) + \log_2(35)\log_2(144)\log_2(3240000)
)}
}
\hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}}
\\
\quad\quad\quad
\overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu} \overline{\rule[11pt]{0pt}{0pt}} \hspace{1mu}
\overline{\rule[11pt]{0pt}{0pt}
·
7^{(
{-(8\log_2(35)\log_2(40)\log_2(45) + \log_2(35)\log_2(144)\log_2(3240000))}
)}
}
}[/math]
Clearly, such an exact value is of dubious interest as is. But it may be nice for some types of personalities (including the present author) to know, theoretically speaking, that this expression gives us the truly optimal size of this generator, where the general solution would only find a close approximation. It would look a little less insane if we were using unity-weight damage, or our complexity didn't include logarithmic values.
At some point we do need to convert this to an inexact decimal form to make any practical use of it. But we should wait until the last possible moment, so as to not let rounding errors compound.
Well, this is that last possible moment. So this value works out to about 1.99847, just shy of 2, which is great because it's supposed to be a tempered octave. In cents it is 1198.679 ¢.
We won't show the exact exponential form for the other generators [math]\displaystyle{ \textbf{g}_2 }[/math] and [math]\displaystyle{ \textbf{g}_3 }[/math]; the point has been made. The practical thing to do is simply multiply this [math]\displaystyle{ G }[/math] by [math]\displaystyle{ 𝒋 }[/math], to find [math]\displaystyle{ 𝒈 }[/math]. We'll go ahead and show things in decimals now:
[math]\displaystyle{
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 & 3368.826 \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
G \\
\left[ \begin{array} {r}
10.156 & 2.701 & 5.530 \\
1.831 & 1.140 & 0.306 \\
3.662 & 1.281 & 2.612 \\
{-7.325} & {-2.561} & {-4.224} \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
1198.679 & 350.516 & 265.929 \\
\end{array} \right]
\end{array}
}[/math]
And so that's the tuning (in cents) we find for this constraint matrix! (But remember, this is only one of many candidates for the minimax tuning here—it is not necessarily the actual minimax tuning. We picked this particular ReDPOTIC / constraint matrix / coinciding-damage point / candidate tuning example basically at random.)
System of equations style
In our simpler example, we looked at our matrix equation as a system of equations. It may be instructive to consider this related approach toward this result.
Suppose instead that rather than going for a matrix solution in [math]\displaystyle{ G }[/math], we went straight for a single vector, our generator tuning map [math]\displaystyle{ 𝒈 }[/math]. In other words, we don't save the conversion from [math]\displaystyle{ G }[/math] to [math]\displaystyle{ 𝒈 }[/math] via [math]\displaystyle{ 𝒋 }[/math] to the end; we build this into our solution. So rewind back to before we did a matrix inverse, and instead we multiply each side of the equation by [math]\displaystyle{ 𝒋 }[/math]. The [math]\displaystyle{ 𝒋G }[/math] goes to [math]\displaystyle{ 𝒈 }[/math], and we just go ahead and multiply its entries [math]\displaystyle{ g_1 }[/math], [math]\displaystyle{ g_2 }[/math], and [math]\displaystyle{ g_3 }[/math] up with everything else:
[math]\displaystyle{
\begin{array} {ccc}
𝒈M\mathrm{T}CK \\
\left[ \begin{array} {rrr}
15.773g_1 & {-0.363g_1} & 1.544g_1 \\
{-21.095g_2} & {-10.621g_2} & 2.041g_2 \\
{-15.773g_3} & 5.854g_3 & {-5.129g_3} \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
𝒋\mathrm{T}CK \\
\left[ \begin{array} {rrr}
7318.250 & {-2600.619} & 1202.397 \\
\end{array} \right]
\end{array}
}[/math]
Now the columns of this can be viewed as a system of equations (so we essentially transpose everything to get this new look):
[math]\displaystyle{
\begin{array} {r}
15.773g_1 & + & {-21.095g_2} & + & {-15.773g_3} & = & 7318.250 \\
{-0.363}g_1 & + & {-10.621g_2} & + & 5.854g_3 & = & {-2600.619} \\
1.544g_1 & + & 2.041g_2 & + & {-5.129g_3} & = & 1202.397 \\
\end{array}
}[/math]
These can all be true at once now (again, before the constraint, they couldn't). The values come out to:
[math]\displaystyle{
g_1 = 1198.679 \\
g_2 = 350.516 \\
g_3 = 265.929
}[/math]
This matches what we found for [math]\displaystyle{ 𝒈 }[/math] via solving for [math]\displaystyle{ G }[/math].
The system of equations style is how Keenan's original algorithm works. The matrix inverse style is Dave's modification which may be less obvious how it works, but is capable of solving for generator embeddings.
Sanity-check
We can sanity check it if we like. This was supposed to find us the tuning of breed temperament where [math]\displaystyle{ \frac75 × \frac85 = \frac{56}{25} }[/math], [math]\displaystyle{ \frac75 × \frac59 = \frac79 }[/math] (or we might prefer to think of it in its superunison form, [math]\displaystyle{ \frac97 }[/math]), and [math]\displaystyle{ \frac75 × \frac34 = \frac{21}{20} }[/math] are pure.
Well, breed maps [math]\displaystyle{ \textbf{i}_1 = \frac{56}{25} }[/math] [3 0 -2 1⟩ to the generator-count vector [math]\displaystyle{ \textbf{y}_1 }[/math] [3 -4 -3}. And [math]\displaystyle{ 𝒈\textbf{y}_1 }[/math] looks like {1198.679 350.516 265.929][3 -4 -3} [math]\displaystyle{ = 1198.679 × 3 + 350.516 x {-4} + 265.929 × {-3} = 1396.186 }[/math]. Its JI size is [math]\displaystyle{ 1200 × \log_2(\frac{56}{25}) = 1396.198 }[/math] which is pretty close; close enough, perhaps, given all the rounding errors we were accumulating.
And breed maps [math]\displaystyle{ \textbf{i}_2 = \frac{9}{7} }[/math] [0 2 0 -1⟩ to the generator-count vector [math]\displaystyle{ \textbf{y}_2 }[/math] [0 2 -1}. And [math]\displaystyle{ 𝒈\textbf{y}_2 }[/math] looks like {1198.679 350.516 265.929][0 2 -1} [math]\displaystyle{ = 1198.679 × 0 + 350.516 × 2 + 265.929 × {-1} = 435.103 }[/math]. Its JI size is [math]\displaystyle{ 1200 × \log_2(\frac97) = 435.084 }[/math], also essentially pure.
Finally breed maps [math]\displaystyle{ \textbf{i}_3 = \frac{21}{20} }[/math] [-2 1 -1 1⟩ to the generator-count vector [math]\displaystyle{ \textbf{y}_3 }[/math] [0 1 -1}. And [math]\displaystyle{ 𝒈\textbf{y}_3 }[/math] looks like {1198.679 350.516 265.929][0 1 -1} [math]\displaystyle{ = 1198.679 × 0 + 350.516 × 1 + 265.929 × {-1} = 84.587 }[/math]. Its JI size is [math]\displaystyle{ 1200 × \log_2(\frac{21}{20}) = 84.467 }[/math], again, essentially pure.
Relation to only-held intervals method and zero-damage method
Note that this [math]\displaystyle{ G = \mathrm{T}CK(M\mathrm{T}CK)^{-1} }[/math] formula is the same thing as the [math]\displaystyle{ G = U(MU)^{-1} }[/math] formula used for the #only held-intervals method; it's just that formula where [math]\displaystyle{ \mathrm{U} = \mathrm{T}CK }[/math]. In other words, we will find a basis for the unchanged intervals of this tuning of this temperament to be:
[math]\displaystyle{
\begin{array} {c}
\mathrm{U} = \mathrm{T}CK \\
\left[ \begin{array} {c}
\log_2(40^3) & 0 & {-\log_2(12^2)} \\
0 & {-\log_2(45^2)} & \log_2(12) \\
{-\log_2(35·40)} & \log_2(\frac{45}{35}) & {-\log_2(35)} \\
\log_2(35) & \log_2(35) & \log_2(35) \\
\end{array} \right]
\end{array}
}[/math]
Owing to our choice to weight our absolute error to obtain damage, these intervals are quite strange. Not only do we have non-integer entries in our prime-count vectors here, we've gone beyond the rational entries we often find for generator embeddings and unchanged-interval bases, etc. and now have irrational entries with freaking logarithms in them. So these aren't particularly insight-giving unchanged-intervals, but they are what they are.
So, in effect, the coinciding-damage method is fairly similar to the zero-damage method. Each point in either method's point set corresponds to an unchanged-interval basis [math]\displaystyle{ \mathrm{U} }[/math]. It is the case that for the zero-damage method the members of this [math]\displaystyle{ \mathrm{U} }[/math] are pulled directly from the target-interval set [math]\displaystyle{ \mathrm{T} }[/math], whereas for the coinciding-damage method here, the members of each [math]\displaystyle{ \mathrm{U} }[/math] have a more complex relationship with the members of [math]\displaystyle{ \mathrm{T} }[/math] set, being products of relative direction pairs of them instead.
With held-intervals
When a tuning scheme has optimization power [math]\displaystyle{ p = ∞ }[/math] and also specifies one or more held-intervals, we can adapt the coinciding-damage method to accommodate this. In short, we can no longer dedicate every generator toward our target-intervals; we must allocate one generator toward each interval to be held unchanged.
Counts of target-intervals with held-intervals
In the earlier section #Generalizing to higher dimensions: counts of target-intervals required to make the points, we looked at how it generally takes [math]\displaystyle{ r + 1 }[/math] target-interval damage graphs to intersect to make a point, but only [math]\displaystyle{ r }[/math] of them on the zero-damage floor.
When there are held-intervals, however, things get a little trickier.
Each additional held-interval added is like taking a cross-section through the tuning damage space, specifically, the cross-section wherever that interval is held unchanged. Tuning damage space is still [math]\displaystyle{ (r + 1) }[/math]-dimensional, but now we only care about a slice through that space, a slice with [math]\displaystyle{ h }[/math] fewer dimensions. That is, it'll be a [math]\displaystyle{ (r + 1 - h) }[/math]-dimensional slice. And within this slice, then, we only need [math]\displaystyle{ r + 1 - h }[/math] target-intervals' damages to coincide to make a point, and only [math]\displaystyle{ r - h }[/math] of them to make a point on the floor.
For example, when tuning an octave-fifth form of meantone temperament, we'd know we'd be searching a 3D tuning damage space, with one floor axis for [math]\displaystyle{ g_1 }[/math] in the vicinity of 1200 ¢ and the other floor axis for [math]\displaystyle{ g_2 }[/math] in the vicinity of 701.955 ¢. But if we say it's a held-octave tuning we want, then while all of our target-interval's hyper-V's are still exactly as they were, fully occupying the three dimensions of this space, but now we only care about the 2D slice through it where [math]\displaystyle{ g_1 = 1200 }[/math].
In that very simple example, only one of the temperament's generators was involved in the mapped interval that the held-interval maps to, so the cross-section is conveniently perpendicular to the axis for that generator, and thus the tuning damage graph with reduced dimension is easy to prepare. However, if we had instead requested a held-{5/4}, then since that maps to [-2 4}, using multiple different generators, then the cross-section will be diagonal across the floor, perpendicular to no generator axes.
Modified constraint matrices
We do this by changing our constraint matrices [math]\displaystyle{ K }[/math]; rather than building them to represent permutations of relative direction for combinations of [math]\displaystyle{ r + 1 }[/math] target-intervals, instead we only combine [math]\displaystyle{ r + 1 - h }[/math] target-intervals for each of these constraint matrices, where [math]\displaystyle{ h }[/math] is the count of held-intervals. As a result of this, each [math]\displaystyle{ K }[/math] has [math]\displaystyle{ h }[/math] fewer columns than before—or at least it would, if we didn't replace these columns with [math]\displaystyle{ h }[/math] new columns, one for each of our [math]\displaystyle{ h }[/math] held-intervals. Remember, each of these constraint matrices gets multiplied together with other matrices that represent information about our temperament and tuning scheme—our targeted intervals, and their weights (if any)—in order to take a system of approximations (represented by matrices) and crunch it down to a smaller system of equalities (still represented by matrices) that can be automatically solved (using a matrix inverse). So, instead of these constraint matrices doing only a single job—enforcing that [math]\displaystyle{ r + 1 }[/math] target-intervals receive coinciding damage, each constraint matrix now handles two jobs at once—enforcing that only [math]\displaystyle{ r + 1 - h }[/math] target-intervals receive coinciding damage, and that [math]\displaystyle{ h }[/math] held-intervals receive zero damage.
In order for the constraint matrices to handle their new second job, however, we must make further changes. The held-intervals must now be accessible in the other matrices that multiply together to form our solvable system of equations. In particular:
- We concatenate the target-interval list [math]\displaystyle{ \mathrm{T} }[/math] and the held-interval basis [math]\displaystyle{ \mathrm{H} }[/math] together to a new matrix [math]\displaystyle{ \mathrm{T}|\mathrm{H} }[/math].
- We accordingly extend the weight matrix [math]\displaystyle{ W }[/math] diagonally so that matrix shapes work out for multiplication purposes, or said another way, so that each held-interval appended to [math]\displaystyle{ \mathrm{T} }[/math] gets matched up with a dummy weight.[note 20]
Prepare constraint matrix
Let's demonstrate this by example. We'll revise the example we looked at in the earlier "bigger example" section, with 3 generators ([math]\displaystyle{ r = 3 }[/math]) and 10 target-intervals ([math]\displaystyle{ k = 10 }[/math]). The specific example constraint matrix we looked at, therefore, was an [math]\displaystyle{ (k, r) }[/math]-shaped matrix, which related [math]\displaystyle{ r + 1 = 4 }[/math] of those target-intervals together with coinciding damage:
[math]\displaystyle{
\begin{array} {rrr}
\scriptsize{6/5} \\
\scriptsize{7/5} \\
\scriptsize{8/5} \\
\scriptsize{9/5} \\
\scriptsize{7/6} \\
\scriptsize{4/3} \\
\scriptsize{3/2} \\
\scriptsize{8/7} \\
\scriptsize{9/7} \\
\scriptsize{9/8} \\
\end{array}
\left[ \begin{array} {rrr}
0 & 0 & 0 \\
+1 & +1 & +1 \\
+1 & 0 & 0 \\
0 & {-1} & 0 \\
0 & 0 & 0 \\
0 & 0 & {-1} \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{array} \right]
}[/math]
For a tuning scheme with [math]\displaystyle{ h = 1 }[/math], however, we can only get three target-intervals to have coinciding damage at the same time. So we'd never see this constraint matrix for such a scheme. Instead, any example constraint matrix we'd pick would only have two such rows. In order to keep working with something similar to this example, then, let's just drop the last column:
[math]\displaystyle{
\begin{array} {rrr}
\scriptsize{6/5} \\
\scriptsize{7/5} \\
\scriptsize{8/5} \\
\scriptsize{9/5} \\
\scriptsize{7/6} \\
\scriptsize{4/3} \\
\scriptsize{3/2} \\
\scriptsize{8/7} \\
\scriptsize{9/7} \\
\scriptsize{9/8} \\
\end{array}
\left[ \begin{array} {rrr}
0 & 0 \\
+1 & +1 \\
+1 & 0 \\
0 & {-1} \\
0 & 0 \\
0 & 0 \\
0 & 0 \\
0 & 0 \\
0 & 0 \\
0 & 0 \\
\end{array} \right]
}[/math]
But we still want a third column; we still have [math]\displaystyle{ r = 3 }[/math] generators in this example. But now we need to specify that one of these generators needs to accomplish the job of tuning our held-interval exactly. We do that by adding a column that's all zeros except for a single nonzero entry in the row for that held-interval (if it's not clear how this enforces that interval to be unchanged, don't worry; it will become clear in a later step when we translate this system of matrices to the system of linear equations which it is essentially shorthand notation for):
[math]\displaystyle{
\begin{array} {rrr}
\scriptsize{6/5} \\[2pt]
\scriptsize{7/5} \\[2pt]
\scriptsize{8/5} \\[2pt]
\scriptsize{9/5} \\[2pt]
\scriptsize{7/6} \\[2pt]
\scriptsize{4/3} \\[2pt]
\scriptsize{3/2} \\[2pt]
\scriptsize{8/7} \\[2pt]
\scriptsize{9/7} \\[2pt]
\scriptsize{9/8} \\[2pt]
\style{background-color:#FFF200;padding:5px}{\scriptsize{5/3}} \\[2pt]
\end{array}
\left[ \begin{array} {rrr}
0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
+1 & +1 & \style{background-color:#FFF200;padding:5px}{0}\\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & {-1} & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
}[/math]
Oh, right—we didn't have a row for this held-interval yet. All the rows we had before were for our target-intervals. No big deal, though. We just added an extra row for this, our held-interval, and we can fill out the new entries it creates in the other columns with zeros.
Modified tempered and just sides of to-be equality
The consequences of adding this row are more far-reaching than our [math]\displaystyle{ K }[/math] matrices, however. Remember, these multiply with [math]\displaystyle{ M\mathrm{T}C }[/math] on the left-hand side of the equal sign and [math]\displaystyle{ \mathrm{T}C }[/math] on the right-hand side. So matrix shapes have to keep matching for matrix multiplication to remain possible. We just changed the shape of [math]\displaystyle{ K }[/math] from an [math]\displaystyle{ (k, r) }[/math]-shaped matrix to a [math]\displaystyle{ (k + h, r) }[/math]-shaped matrix. The shape of [math]\displaystyle{ M\mathrm{T}C }[/math] is [math]\displaystyle{ (r, k) }[/math] and the shape of [math]\displaystyle{ \mathrm{T}C }[/math] is [math]\displaystyle{ (d, k) }[/math]. So if we want these shapes to keep matching, we need to change them to [math]\displaystyle{ (r, k + h) }[/math] and [math]\displaystyle{ (d, k + h) }[/math], respectively.
Now that's a rather dry way of putting it. Let's put it in more natural terms. We know what these additions to [math]\displaystyle{ M\mathrm{T}C }[/math] and [math]\displaystyle{ \mathrm{T}C }[/math] are about: they're the held-intervals that the new entries we added to the constraint matrices are referring to! In particular, we need to expand [math]\displaystyle{ \mathrm{T} }[/math] (the actual target-intervals we chose here are arbitrary and don't really matter for this example):
[math]\displaystyle{
\begin{array} {ccc}
\mathrm{T} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r|r}
1 & 0 & 3 & 0 & {-1} & 2 & {-1} & 3 & 0 & {-3} \\
1 & 0 & 0 & 2 & {-1} & {-1} & 1 & 0 & 2 & 2 \\
{-1} & {-1} & {-1} & {-1} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 1 & 0 & 0 & {-1} & {-1} & 0 \\
\end{array} \right]
\end{array}
}[/math]
to include the held-intervals. We can just tack them on at the end. We said [math]\displaystyle{ h = 1 }[/math], that is, that we only have one held-interval, but we haven't picked what it is yet. This is also arbitrary for this example. How about we go with [math]\displaystyle{ \frac53 }[/math], with prime-count vector [0 -1 1 0⟩:
[math]\displaystyle{
\begin{array} {ccc}
\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r|r|r}
1 & 0 & 3 & 0 & {-1} & 2 & {-1} & 3 & 0 & {-3} & \style{background-color:#FFF200;padding:5px}{0} \\
1 & 0 & 0 & 2 & {-1} & {-1} & 1 & 0 & 2 & 2 & \style{background-color:#FFF200;padding:5px}{-1} \\
{-1} & {-1} & {-1} & {-1} & 0 & 0 & 0 & 0 & 0 & 0 & \style{background-color:#FFF200;padding:5px}{1} \\
0 & 1 & 0 & 0 & 1 & 0 & 0 & {-1} & {-1} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
}[/math]
We've got to extend [math]\displaystyle{ C }[/math] too. We can pick any weight we want, other than 0. You'll see why when we work out the system of equations in a moment):
[math]\displaystyle{
\begin{array} {ccc}
C \\
\text{diag}(\log_2(\left[ \begin{array} {rrr}
30 & 35 & 40 & 45 & 42 & 12 & 6 & 56 & 63 & 72 & \style{background-color:#FFF200;padding:5px}{2} \\
\end{array} \right]))
\end{array}
}[/math]
(Note that the last entry appears as 2 here, because we placed the [math]\displaystyle{ \log_2 }[/math] outside the array brackets.)
There's no need to mess with [math]\displaystyle{ M }[/math] here.
Prepare tempered and just sides of to-be equality
As before, let's work out [math]\displaystyle{ M\mathrm{T}C }[/math] and [math]\displaystyle{ \mathrm{T}C }[/math] separately, then constrain each of them with [math]\displaystyle{ K }[/math], then put them together in a linear system of equations, solving for the generator tuning map [math]\displaystyle{ 𝒈 }[/math]. Though this time around, all occurrences of [math]\displaystyle{ \mathrm{T} }[/math] will be replaced with [math]\displaystyle{ \mathrm{T|\style{background-color:#FFF200;padding:2px}{H}} }[/math].
First, [math]\displaystyle{ M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})C }[/math]:
[math]\displaystyle{
\scriptsize
\begin{array} {ccc}
M \\
\left[ \begin{array} {rrr}
1 & 1 & 1 & 2 \\
0 & 2 & 3 & 2 \\
0 & 0 & 2 & 1
\end{array} \right]
\end{array}
\begin{array} {ccc}
\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r|r|r}
1 & 0 & 3 & 0 & {-1} & 2 & {-1} & 3 & 0 & {-3} & \style{background-color:#FFF200;padding:5px}{0} \\
1 & 0 & 0 & 2 & {-1} & {-1} & 1 & 0 & 2 & 2 & \style{background-color:#FFF200;padding:5px}{-1} \\
{-1} & {-1} & {-1} & {-1} & 0 & 0 & 0 & 0 & 0 & 0 & \style{background-color:#FFF200;padding:5px}{1} \\
0 & 1 & 0 & 0 & 1 & 0 & 0 & {-1} & {-1} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
C \\
\text{diag}(\log_2(\left[ \begin{array} {rrr}
30 & 35 & 40 & 45 & 42 & 12 & 6 & 56 & 63 & 72 & \style{background-color:#FFF200;padding:5px}{2} \\
\end{array} \right]))
\end{array}
}[/math]
Which works out to:
[math]\displaystyle{
\small
\begin{array} {ccc}
M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r}
\log_2(30) & \log_2(35) & 2\log_2(40) & \log_2(45) & 0 & \log_2(12) & 0 & \log_2(56) & 0 & {-\log_2(72)} & \style{background-color:#FFF200;padding:5px}{0} \\
{-\log_2(30)} & {-\log_2(35)} & {-3\log_2(40)} & \log_2(45) & 0 & {-2\log_2(12)} & 2\log_2(6) & {-2\log_2(56)} & 2\log_2(63) & 4\log_2(72) & \style{background-color:#FFF200;padding:5px}{1} \\
{-2\log_2(30)} & {-\log_2(35)} & {-2\log_2(40)} & {-2\log_2(45)} & \log_2(42) & 0 & 0 & {-\log_2(56)} & {-\log_2(63)} & 0 & \style{background-color:#FFF200;padding:5px}{2} \\
\end{array} \right]
\end{array}
}[/math]
So that's the same as before, but with the extra column at the right, which is alone in having integer entries owing to its weight being the integer 1. What we're seeing there is that [0 -1 1 0⟩ maps to [0 1 2} in this temperament, that's all.
Now, we do [math]\displaystyle{ (\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})C }[/math]:
[math]\displaystyle{
\small
\begin{array} {ccc}
\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}} \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r|r|r}
1 & 0 & 3 & 0 & {-1} & 2 & {-1} & 3 & 0 & {-3}
& \style{background-color:#FFF200;padding:5px}{0} \\
1 & 0 & 0 & 2 & {-1} & {-1} & 1 & 0 & 2 & 2
& \style{background-color:#FFF200;padding:5px}{-1} \\
{-1} & {-1} & {-1} & {-1} & 0 & 0 & 0 & 0 & 0 & 0
& \style{background-color:#FFF200;padding:5px}{1} \\
0 & 1 & 0 & 0 & 1 & 0 & 0 & {-1} & {-1} & 0
& \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
C \\
\text{diag}(\log_2(\left[ \begin{array} {rrr}
30 & 35 & 40 & 45 & 42 & 12 & 6 & 56 & 63 & 72 & \style{background-color:#FFF200;padding:5px}{2} \\
\end{array} \right]))
\end{array}
= \\[50pt] \small
\begin{array} {ccc}
(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r}
\log_2(30) & 0 & \log_2(40) & 0 & {-\log_2(42)} & 2\log_2(12) & {-\log_2(6)} & 3\log_2(56) & 0 & {-3\log_2(72)} & \style{background-color:#FFF200;padding:5px}{0} \\
\log_2(30) & 0 & 0 & 2\log_2(45) & {-\log_2(42)} & {-\log_2(12)} & \log_2(6) & 0 & 2\log_2(63) & 2\log_2(72) & \style{background-color:#FFF200;padding:5px}{-1} \\
{-\log_2(30)} & {-\log_2(35)} & {-\log_2(40)} & {-\log_2(45)} & 0 & 0 & 0 & 0 & 0 & 0 & \style{background-color:#FFF200;padding:5px}{1} \\
0 & \log_2(35) & 0 & 0 & \log_2(42) & 0 & 0 & {-\log_2(56)} & {-\log_2(63)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
}[/math]
Again, same as before, but with one more column on the right now.
Apply constraint
Now, let's constrain both sides. First, the left side:
[math]\displaystyle{
\scriptsize
\begin{array} {ccc}
M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r}
\log_2(30) & \log_2(35) & 2\log_2(40) & \log_2(45) & 0 & \log_2(12) & 0 & \log_2(56) & 0 & {-\log_2(72)} & \style{background-color:#FFF200;padding:5px}{0} \\
{-\log_2(30)} & {-\log_2(35)} & {-3\log_2(40)} & \log_2(45) & 0 & {-2\log_2(12)} & 2\log_2(6) & {-2\log_2(56)} & 2\log_2(63) & 4\log_2(72) & \style{background-color:#FFF200;padding:5px}{1} \\
{-2\log_2(30)} & {-\log_2(35)} & {-2\log_2(40)} & {-2\log_2(45)} & \log_2(42) & 0 & 0 & {-\log_2(56)} & {-\log_2(63)} & 0 & \style{background-color:#FFF200;padding:5px}{2} \\
\end{array} \right]
\end{array}
\begin{array}
K \\
\left[ \begin{array} {rrr}
0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
+1 & +1 & \style{background-color:#FFF200;padding:5px}{0}\\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & {-1} & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
→ \\
\begin{array} {c}
M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK \\
\left[ \begin{array} {c}
\log_2(35·40^2) & {-\log_2(\frac{45}{35})} & \style{background-color:#FFF200;padding:5px}{0} \\
{-\log_2(35·40^3)} & {-\log_2(35·45)} & \style{background-color:#FFF200;padding:5px}{1} \\
{-\log_2(35·40^2)} & \log_2(\frac{45^2}{35}) & \style{background-color:#FFF200;padding:5px}{2} \\
\end{array} \right]
\end{array}
}[/math]
Same as before, with the rightmost column replaced with a column for our held-interval.
And now the right side:
[math]\displaystyle{
\scriptsize
\begin{array} {ccc}
(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})C \\
\left[ \begin{array} {r|r|r|r|r|r|r|r|r}
\log_2(30) & 0 & \log_2(40) & 0 & {-\log_2(42)} & 2\log_2(12) & {-\log_2(6)} & 3\log_2(56) & 0 & {-3\log_2(72)} & \style{background-color:#FFF200;padding:5px}{0} \\
\log_2(30) & 0 & 0 & 2\log_2(45) & {-\log_2(42)} & {-\log_2(12)} & \log_2(6) & 0 & 2\log_2(63) & 2\log_2(72) & \style{background-color:#FFF200;padding:5px}{-1} \\
{-\log_2(30)} & {-\log_2(35)} & {-\log_2(40)} & {-\log_2(45)} & 0 & 0 & 0 & 0 & 0 & 0 & \style{background-color:#FFF200;padding:5px}{1} \\
0 & \log_2(35) & 0 & 0 & \log_2(42) & 0 & 0 & {-\log_2(56)} & {-\log_2(63)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
\begin{array}
K \\
\left[ \begin{array} {rrr}
0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
+1 & +1 & \style{background-color:#FFF200;padding:5px}{0}\\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & {-1} & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
0 & 0 & \style{background-color:#FFF200;padding:5px}{0}\\
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
→ \\
\begin{array} {c}
(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK \\
\left[ \begin{array} {c}
\log_2(40^3) & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & {-\log_2(45^2)} & \style{background-color:#FFF200;padding:5px}{{-1}} \\
{-\log_2(35·40)} & \log_2(\frac{45}{35}) & \style{background-color:#FFF200;padding:5px}{1} \\
\log_2(35) & \log_2(35) & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
}[/math]
Again, same as before, but with the rightmost column replaced with a column for our held-interval.
Now, put them together, with [math]\displaystyle{ G }[/math] on the left-hand side, as an equality:
[math]\displaystyle{
\small
\begin{array} {c}
G \\
\left[ \begin{array} {c}
g_{11} & g_{12} & g_{13} \\
g_{21} & g_{22} & g_{23} \\
g_{31} & g_{32} & g_{33} \\
g_{41} & g_{42} & g_{43} \\
\end{array} \right]
\end{array}
\begin{array} {c}
M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK \\
\left[ \begin{array} {c}
\log_2(35·40^2) & {-\log_2(\frac{45}{35})} & \style{background-color:#FFF200;padding:5px}{0} \\
{-\log_2(35·40^3)} & {-\log_2(35·45)} & \style{background-color:#FFF200;padding:5px}{1} \\
{-\log_2(35·40^2)} & \log_2(\frac{45^2}{35}) & \style{background-color:#FFF200;padding:5px}{2} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK \\
\left[ \begin{array} {c}
\log_2(40^3) & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & {-\log_2(45^2)} & \style{background-color:#FFF200;padding:5px}{{-1}} \\
{-\log_2(35·40)} & \log_2(\frac{45}{35}) & \style{background-color:#FFF200;padding:5px}{1} \\
\log_2(35) & \log_2(35) & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
}[/math]
Solve for generator embedding
At this point, following the pattern from above, we can solve for [math]\displaystyle{ G }[/math] as [math]\displaystyle{ (\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK(M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK)^{-1} }[/math]. The matrix inverse is the step where the exact values in terms of logarithms start to get out of hand. Since we've already proven our point about exactness of the solutions from this method in the earlier "bigger example" section, for easier reading, let's lapse into decimal numbers from this point forward:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {c}
g_{11} & g_{12} & g_{13} \\
g_{21} & g_{22} & g_{23} \\
g_{31} & g_{32} & g_{33} \\
g_{41} & g_{42} & g_{43} \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK \\
\left[ \begin{array} {rrr}
15.966 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & {-10.984} & \style{background-color:#FFF200;padding:5px}{{-1}} \\
{-10.451} & 0.363 & \style{background-color:#FFF200;padding:5px}{1} \\
5.129 & 5.129 & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
\begin{array} {ccc}
(M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK)^{-1} \\
\left[ \begin{array} {rrr}
{-27.097} & 0.725 & {-0.363} \\
26.417 & 31.546 & {-15.773} \\
\style{background-color:#FFF200;padding:5px}{{-291.028}} & \style{background-color:#FFF200;padding:5px}{{-86.624}} & \style{background-color:#FFF200;padding:5px}{{-175.177}} \\
\end{array} \right] \\
\hline
{-436.978}
\end{array}
}[/math]
Note where the yellow-highlights went: inversing transposed them from the rightmost column to the bottom row. It's no longer super clear what these values have to do with the held-interval anymore, however, and that's okay. In the next step, notice that when we multiply together [math]\displaystyle{ (\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK }[/math] and [math]\displaystyle{ (M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK)^{-1} }[/math] that the yellow-highlighted entries will pair up for every individual dot products, and thus that the final matrix product will have a "little bit of yellow" mixed in to every entry. In other words, every entry of [math]\displaystyle{ G }[/math] may potentially participate in achieving the effect that this interval is held unchanged.
So, actually multiplying those up now, we find [math]\displaystyle{ G }[/math] =
[math]\displaystyle{
\begin{array} {c}
(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK(M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK)^{-1} \\
\left[ \begin{array} {c}
0.990 & {-0.0265} & {0.0132} \\
{-0.00199} & 0.595 & {-0.797} \\
{-0.00399} & 0.189 & 0.405 \\
0.00798 & {-0.379} & 0.189 \\
\end{array} \right] \\
\end{array}
}[/math]
Convert generator embedding to generator tuning map
And from here we can find [math]\displaystyle{ 𝒈 = 𝒋G }[/math]:
[math]\displaystyle{
\begin{array} {ccc}
𝒋 \\
\left[ \begin{array} {rrr}
1200.000 & 1901.955 & 2786.314 & 3368.826 \\
\end{array} \right]
\end{array}
\begin{array} {c}
G \\
\left[ \begin{array} {c}
0.990 & {-0.0265} & {0.0132} \\
{-0.00199} & 0.595 & {-0.797} \\
{-0.00399} & 0.189 & 0.405 \\
0.00798 & {-0.379} & 0.189 \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
𝒈 \\
\left[ \begin{array} {rrr}
1200.000 & 350.909 & 266.725 \\
\end{array} \right]
\end{array}
}[/math]
Confirming: yes, {1200.000 350.909 266.725][0 1 2} = [math]\displaystyle{ (1200.000 × 0) + (350.909 × 1) + (266.725 × 2) = 0 + 350.909 + 533.450 = 884.359 }[/math]. So the constraint to hold that interval unchanged has been satisfied.
System of equations style
It may be instructive again to consider the system of equations style, solving directly for [math]\displaystyle{ 𝒈 }[/math]. Rewinding to before we took our matrix inverse, introducing [math]\displaystyle{ 𝒋 }[/math] to both sides, and multiplying the entries of [math]\displaystyle{ 𝒈 }[/math] through, we find:
[math]\displaystyle{
\begin{array} {ccc}
𝒈M(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK \\
\left[ \begin{array} {rrr}
15.773g_1 & {-0.363g_1} & \style{background-color:#FFF200;padding:5px}{0g_1} \\
{-21.095g_2} & {-10.621g_2} & \style{background-color:#FFF200;padding:5px}{1g_2} \\
{-15.773g_3} & 5.854g_3 & \style{background-color:#FFF200;padding:5px}{2g_3} \\
\end{array} \right]
\end{array}
=
\begin{array} {ccc}
𝒋(\mathrm{T|\style{background-color:#FFF200;padding:2px}{H}})CK \\
\left[ \begin{array} {rrr}
7318.250 & {-2600.619} & \style{background-color:#FFF200;padding:5px}{884.359} \\
\end{array} \right]
\end{array}
}[/math]
Which gets viewed as a system of equations:
[math]\displaystyle{
\begin{array} {r}
15.773g_1 & + & {-21.095g_2} & + & {-15.773g_3} & = & 7318.250 \\
{-0.363}g_1 & + & {-10.621g_2} & + & 5.854g_3 & = & {-2600.619} \\
\style{background-color:#FFF200;padding:5px}{0g_1} & + & \style{background-color:#FFF200;padding:5px}{1g_2} & + & \style{background-color:#FFF200;padding:5px}{2g_3} & = & \style{background-color:#FFF200;padding:5px}{884.359} \\
\end{array}
}[/math]
The third equation—which in the earlier "bigger example" was used to enforce that a fourth target-interval received coinciding damage to the other three target-intervals tapped by the constraint matrix—here has been replaced with an equation that enforces that [0 1 2}, the generator-count vector that [math]\displaystyle{ \frac53 }[/math] maps to in this temperament, is equal to the just tuning of that same interval. And so, when we solve this system of equations, we now get a completely different set of generator tunings.
[math]\displaystyle{
g_1 = 1200.000 \\
g_2 = 350.909 \\
g_3 = 266.725 \\
}[/math]
Which agrees with what we found by solving directly for [math]\displaystyle{ G }[/math].
Sanity-check
But is this a minimax tuning candidate still? That is, do we find that in the damage list for this tuning, that the three target-intervals whose damages were requested to coincide, are still coinciding? Indeed we do:
[math]\displaystyle{
\begin{array} {c}
\textbf{d} \\
\left[ \begin{array} {r}
0.007 & 0.742 & 0.742 & 0.742 & 0.788 & 0.495 & 0.353 & 1.650 & 0.057 & 1.694 \\
\end{array} \right]
\end{array}
}[/math]
We can see that the 2nd, 3rd, and 4th target-intervals, the ones with non-zero entries in their columns of [math]\displaystyle{ K }[/math], all coincide with 0.742 damage, so this is a proper candidate for minimax tuning here. It's some point where three damage graphs are intersecting while within the held-interval plane. Rinse and repeat.
Tie-breaking
We've noted that the zero-damage method for miniaverage tuning schemes cannot directly handle non-unique methods itself. When it finds a non-unique miniaverage (more than one set of generator tunings cause the same minimum sum damage), the next step is to start over with a different method, specifically, the power-limit method, which can only provide an approximate solution.
On the other hand, the coinciding-damage method discussed here, the one for minimax tuning schemes, does have the built-in ability to find a unique true optimum tuning when the minimax tuning is non-unique. In fact, it has not just one, but two different techniques for tie-breaking when it encounters non-unique minimax tunings:
- Comparing ADSLODs. This stands for "abbreviated descending-sorted list of damage". When we have a tied minimax, we essentially have a tie between the first entries of each candidate tuning's ADSLOD. But we can compare more than just the first entry (though we can't compare all entries; hence the "abbreviated" part). If we can break the tie with any of the remaining ADSLOD entries, then we've just done "'basic tie-breaking"'.
- Repeat iterations. When basic tie-breaking fails, we must perform a whole additional iteration of the entire conciding-damage method, but this time only within a narrowed-down region of tuning damage space. Whenever this happens, we've moved on to advanced tie-breaking. More than one repeat iteration may be necessary before a true unique optimum tuning is found (but a round of basic-tiebreaking will occur before each next more advanced iteration of the method.)
Here's a flow chart giving the overall picture:
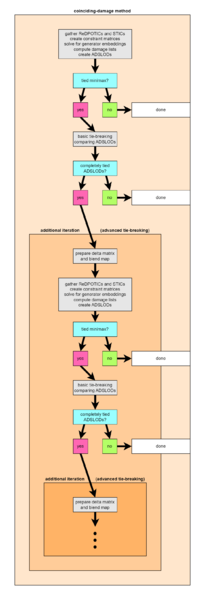
Basic tie-breaking example: Setup
Let's just dive into an example.
The example given in the diagrams back in article 3 here and article 6 here were a bit silly. The easiest way to break the tie in this case would be to remove the offending target-interval from the set, since with constant damage, it will not aid in preferring one tuning to another. More natural examples of tied tunings—that cannot be resolved so easily—require 3D tuning damage space. So that's what we'll be looking at here.
Suppose we're doing a minimax-U tuning of blackwood temperament, and our target-interval set is [math]\displaystyle{ \{ \frac21, \frac31, \frac51, \frac65 \} }[/math]. This is a rank-2 temperament, so we're in 3D tuning damage space. The relevant region of its tuning damage space is visualized below. The yellow hyper-V is the damage graph for [math]\displaystyle{ \frac21 }[/math], the blue hyper-V is for [math]\displaystyle{ \frac31 }[/math], the green hyper-V is for [math]\displaystyle{ \frac51 }[/math], and the red hyper-V is for [math]\displaystyle{ \frac65 }[/math].
Because the mapped intervals for [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math] both use only the first generator [math]\displaystyle{ g_1 }[/math], this means that their hyper-V creases on the floor are parallel. A further consequence of this is that their hyper-Vs' line of intersection above the floor is parallel to the zero-damage floor and will never touch it. Said another way, there's no tuning of blackwood temperament where both prime [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math] are tuned pure at the same time. (This can also be understood through the nature of the blackwood comma [math]\displaystyle{ \frac{256}{243} }[/math], which contains only primes 2 and 3.)
So, instead of a unique minimax tuning point, we instead find this line-segment range of valid minimax tunings, bounded by the points on either end where the damage to the other target-intervals exceeds this coinciding damage to primes math>\frac21</math> and [math]\displaystyle{ \frac31 }[/math]. We indicated this range on the diagram above. At this point, looking down on the surface of our max damage graph, we know the true optimum tuning is somewhere along this range. But it's hard to tell exactly where. In order to find it, let's gather ReDPOTICs and STICs, convert them to constraint matrices, and convert those in turn to tunings.
Basic tie-breaking example: Comparing tunings for minimax
With four target-intervals, we have sixteen ReDPOTICs to check, and six STICs to check, for a total of 22 points. Here are their constraints, tunings, and damage lists:
| Constraint matrix | Candidate generator tuning map | Target-interval damage list | |
|---|---|---|---|
| [math]\displaystyle{ K }[/math] | [math]\displaystyle{ 𝒈_i }[/math] | {[math]\displaystyle{ g_1 }[/math] [math]\displaystyle{ g_2 }[/math]] | [math]\displaystyle{ \textbf{d} }[/math] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ +1 & 0 \\ 0 & +1 \\ 0 & 0 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_1 }[/math] | {238.612 2793.254] | [6.940 6.940 6.940 6.940] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ +1 & 0 \\ 0 & -1 \\ 0 & 0 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_2 }[/math] | {238.612 2779.374] | [6.940 6.940 6.940 6.940] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ -1 & 0 \\ 0 & +1 \\ 0 & 0 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_3 }[/math] | {233.985 2816.390] | [30.075 30.075 30.075 30.075] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ -1 & 0 \\ 0 & -1 \\ 0 & 0 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_4 }[/math] | {233.985 2756.240] | [30.075 30.075 30.075 30.075] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ +1 & 0 \\ 0 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_2 }[/math] | {238.612 2779.374] | [6.940 6.940 6.940 6.940] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ +1 & 0 \\ 0 & 0 \\ 0 & -1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_1 }[/math] | {238.612 2793.254] | [6.940 6.940 6.940 6.940] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ -1 & 0 \\ 0 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_5 }[/math] | {233.985 2696.090] | [30.075 30.075 90.225 30.075] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ -1 & 0 \\ 0 & 0 \\ 0 & -1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_4 }[/math] | {233.985 2756.240] | [30.075 30.075 30.075 30.075] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ 0 & 0 \\ +1 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_6 }[/math] | {239.215 2790.240] | [3.923 11.769 3.923 3.923] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ 0 & 0 \\ +1 & 0 \\ 0 & -1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_1 }[/math] | {238.612 2793.254] | [6.940 6.940 6.940 6.940] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ 0 & 0 \\ -1 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_2 }[/math] | {238.612 2779.374] | [6.940 6.940 6.940 6.940] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & +1 \\ 0 & 0 \\ -1 & 0 \\ 0 & -1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_4 }[/math] | {233.985 2756.240] | [30.075 30.075 30.075 30.075] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} 0 & 0 \\ +1 & +1 \\ +1 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_7 }[/math] | {238.133 2783.200] | [9.334 3.111 3.111 3.111] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} 0 & 0 \\ +1 & +1 \\ +1 & 0 \\ 0 & -1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_2 }[/math] | {238.612 2779.374] | [6.940 6.940 6.940 6.940] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} 0 & 0 \\ +1 & +1 \\ -1 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_1 }[/math] | {238.612 2793.254] | [6.940 6.940 6.940 6.940] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} 0 & 0 \\ +1 & +1 \\ -1 & 0 \\ 0 & -1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_4 }[/math] | {233.985 2756.240] | [30.075 30.075 30.075 30.075] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & 0 \\ 0 & +1 \\ 0 & 0 \\ 0 & 0 \\ \end{array} \right] }[/math] | n/a | n/a | n/a |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & 0 \\ 0 & 0 \\ 0 & +1 \\ 0 & 0 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_8 }[/math] | {240.000 2786.314] | [0.000 18.045 0.000 18.045] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} +1 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_9 }[/math] | {240.000 2804.360] | [0.000 18.045 18.045 0.000] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} 0 & 0 \\ +1 & 0 \\ 0 & +1 \\ 0 & 0 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_{10} }[/math] | {237.744 2786.314] | [11.278 0.000 0.000 11.278] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} 0 & 0 \\ +1 & 0 \\ 0 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_{11} }[/math] | {237.744 2775.040] | [11.278 0.000 11.278 0.000] |
| [math]\displaystyle{ \left[ \begin{array} {rrr} 0 & 0 \\ 0 & 0 \\ +1 & 0 \\ 0 & +1 \\ \end{array} \right] }[/math] | [math]\displaystyle{ 𝒈_{12} }[/math] | {238.612 2786.314] | [6.940 6.940 0.000 0.000] |
Note that many of these constraint matrices ended up identifying the same tuning. Because of relationships between the prime factors of the target-intervals, some of these points in tuning damage space turned out to be the same, or at least vertically aligned, thus giving the same tuning. So, we didn't actually end up with 22 different candidate [math]\displaystyle{ 𝒈_i }[/math] to compare. We only got 12 different candidate tunings. (Also note that one of our constraint matrices failed to find any tuning at all! That's the one that tried to find the place where [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math] are pure simultaneously. Like we said, it cannot be done.)
Let's rework this table a bit. We won't worry about the constraint matrices we used to get here anymore; done with those. We'll just worry about the unique candidate tunings, their damage lists, and we'll add a new column for their maximum values.
| Candidate generator tuning map | Target-interval damage list | Max damage | |
|---|---|---|---|
| [math]\displaystyle{ 𝒈_i }[/math] | {[math]\displaystyle{ g_1 }[/math] [math]\displaystyle{ g_2 }[/math]] | [math]\displaystyle{ \textbf{d} }[/math] | [math]\displaystyle{ \max(\textbf{d}) }[/math] |
| [math]\displaystyle{ 𝒈_1 }[/math] | {238.612 2793.254] | [6.940 6.940 6.940 6.940] | 6.940 |
| [math]\displaystyle{ 𝒈_2 }[/math] | {238.612 2779.374] | [6.940 6.940 6.940 6.940] | 6.940 |
| [math]\displaystyle{ 𝒈_3 }[/math] | {233.985 2816.390] | [30.075 30.075 30.075 30.075] | 30.075 |
| [math]\displaystyle{ 𝒈_4 }[/math] | {233.985 2756.240] | [30.075 30.075 30.075 30.075] | 30.075 |
| [math]\displaystyle{ 𝒈_5 }[/math] | {233.985 2696.090] | [30.075 30.075 90.225 30.075] | 90.225 |
| [math]\displaystyle{ 𝒈_6 }[/math] | {239.215 2790.240] | [3.923 11.769 3.923 3.923] | 11.769 |
| [math]\displaystyle{ 𝒈_7 }[/math] | {238.133 2783.200] | [9.334 3.111 3.111 3.111] | 9.334 |
| [math]\displaystyle{ 𝒈_8 }[/math] | {240.000 2786.314] | [0.000 18.045 0.000 18.045] | 18.045 |
| [math]\displaystyle{ 𝒈_9 }[/math] | {240.000 2804.360] | [0.000 18.045 18.045 0.000] | 18.045 |
| [math]\displaystyle{ 𝒈_{10} }[/math] | {237.744 2786.314] | [11.278 0.000 0.000 11.278] | 11.278 |
| [math]\displaystyle{ 𝒈_{11} }[/math] | {237.744 2775.040] | [11.278 0.000 11.278 0.000] | 11.278 |
| [math]\displaystyle{ 𝒈_{12} }[/math] | {238.612 2786.310] | [6.940 6.940 0.000 0.000] | 6.940 |
From here, we try to pick our minimax tuning. Skimming the last column of this table quickly, we can see that the minimum out of all of our maximum damages is 6.940.
However, alas! We can minimize the maximum damage to this amount using not just one of these candidate generator tuning maps, and not just two of them, but three different ones of them all achieve this feat. Well, we'll just have to tie-break between them, then.
Basic tie-breaking example: Understanding the tie
The tied minimax tunings are [math]\displaystyle{ 𝒈_1 }[/math], [math]\displaystyle{ 𝒈_2 }[/math], and [math]\displaystyle{ 𝒈_{12} }[/math]. These have tuning maps of {238.612 2793.254], {238.612 2779.374], and {238.612 2786.314], respectively. Notice that all three of these give the same tuning for the first generator, [math]\displaystyle{ g_1 }[/math], namely, 238.612 ¢. This tells us that these three tunings can be found on a line together, and it also tells us that this line is perpendicular to the axis for [math]\displaystyle{ g_1 }[/math]. As for the tuning of the second generator [math]\displaystyle{ g_2 }[/math], then, there's going to be one of these three tuning maps which gives the value in-between the other two; that happens here to be the last one, [math]\displaystyle{ 𝒈_{12} }[/math]. Its [math]\displaystyle{ g_2 }[/math] value is 2786.314 ¢, which is in fact exactly halfway between the other two tuning maps' tuning of [math]\displaystyle{ g_2 }[/math], at 2779.374 ¢ and 2793.254 ¢ (you may also notice that 2786.314 is the just tuning of [math]\displaystyle{ \frac51 }[/math]).
Based on what we know from visualizing the tuning damage space earlier, we can suppose that candidate tunings [math]\displaystyle{ 𝒈_1 }[/math] and [math]\displaystyle{ 𝒈_2 }[/math] are the ones that bound the ends of the line segment region of tied minimax tunings. Remember, [math]\displaystyle{ 𝒈_1 }[/math], [math]\displaystyle{ 𝒈_2 }[/math], and [math]\displaystyle{ 𝒈_{12} }[/math] are not really the only tunings tied for minimax tuning; they're merely special/important/representative tunings that are tied for minimax damage. In concrete terms, it's not just {238.612 2793.254], {238.612 2779.374], and {238.612 2786.314] that deal the minimax damage of 6.940. Any tuning with [math]\displaystyle{ g_1 = 238.612 }[/math] and [math]\displaystyle{ 2779.374 \leq g_2 \leq 2793.254 }[/math] deals this same minimax damage, such as {238.612 2794.000] or {238.612 2787.878]. Any of those will satisfy someone looking only to minimax damage. But we're looking for a true optimum in here. We know there will be some other reason to prefer one of these to all the others.
As for [math]\displaystyle{ 𝒈_{12} }[/math], it's halfway between [math]\displaystyle{ 𝒈_1 }[/math] and [math]\displaystyle{ 𝒈_2 }[/math], although from this view we can't specifically see it. That's because this tuning came from one of our constraint matrices we built from a STIC, which is to say that it's for one of our zero-damage points, where target-interval tuning damage graph creases cross each other along the zero-damage floor. So to see this point better, we'll need to rotate our view on tuning damage space, and take a look from below.
We've drawn a dashed white line segment to indicate the basic minimax tied range from the previous diagram, which is along the crease between the blue and yellow graphs. That part of their crease is not directly visible here, because it's exactly the part that's covered up by that green bit in the middle. Then, we've drawn a finely-dotted cyan line straight down from that basic minimax tied range's line segment at a special point: where the green and red creases cross.
Yes, that's right: it turns out that the place the green and red creases cross is directly underneath the line where the blue and yellow creases cross. This is no coincidence. As hinted at earlier, it's because of our choices of target-intervals, and in particular their prime compositions. If you think about it, along the blue/yellow crease, that's where blue [math]\displaystyle{ \frac21 }[/math] and yellow [math]\displaystyle{ \frac31 }[/math] have the same damage. But there's two places where that happens: where they have the same exact error, and where they have the same error but opposite sign (one error is positive and the other negative). This happens to be the latter type of crossing. And also remember that we're using a unity-weight damage here, i.e. where damage is equal to absolute error. So if [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math] have opposite error, that means that their errors cancel out when you combine them to the interval [math]\displaystyle{ \frac61 }[/math]. So [math]\displaystyle{ \frac61 }[/math] is tuned pure along this crease (if this isn't clear, please review #The meaning of the ReDPOTIC product). And along the green [math]\displaystyle{ \frac51 }[/math] damage graph's crease along the zero-damage floor, [math]\displaystyle{ \frac51 }[/math] has zero-damage, i.e. is also pure. So wherever that green crease passes under the blue/yellow crease, that means that both [math]\displaystyle{ \frac61 }[/math] and [math]\displaystyle{ \frac51 }[/math] are pure there. So what should we expect to find with the red hyper-V here, the one for [math]\displaystyle{ \frac65 }[/math]? Well, being comprised exactly and only of [math]\displaystyle{ \frac61 }[/math] and [math]\displaystyle{ \frac51 }[/math], which are both tuned pure, it too must be tuned pure. So no surprise that the red graph crease crosses under the blue/yellow crease at the exact same point as the green crease does.
This—as you will probably not be surprised—is our third tied candidate tuning, [math]\displaystyle{ 𝒈_{12} }[/math], the one that also happens to be halfway between [math]\displaystyle{ 𝒈_1 }[/math] and [math]\displaystyle{ 𝒈_2 }[/math]. We identified this as a point of interest on account of the fact that two damage graphs crossed along the zero-damage floor, thus giving us enough damage graphs to specify a point. This isn't just any point along the floor: again, this point came from one of our STICs.
Intuitively, we should know at this time that this is our true optimum tuning, and we have labeled it as such in the diagram. Any other point along the white dashed line, in our basic minimax region, will minimax damage to [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math] at 6.940 ¢(U). But if we go anywhere along this line segment region other than this one special point, the damage to our other two target-intervals, [math]\displaystyle{ \frac51 }[/math] and [math]\displaystyle{ \frac65 }[/math], will be greater than 0. Sure, the main thing we've been tasked with is to minimize the maximum damage. But while we're at it, why not go the extra mile and tune both [math]\displaystyle{ \frac51 }[/math] and [math]\displaystyle{ \frac65 }[/math] as accurately as we can, too? We might as well. And so [math]\displaystyle{ 𝒈_{12} }[/math] is the best we can do, in a "nested minimax" sense; that's our true optimum tuning. In other words, the maximum damages in each position of these descending-sorted lists are minimized, at least as far down the descending-sorted damage list as they've been abbreviated. (We noted earlier that these zero-damage points might seem unlikely to play much use in identifying a minimax tuning. Well, here's a perfect example of where one saved the day!)
But the question remains: how will the computer be best able to tell that this is the tuning to choose? For that, we're going to need ADSLODs.
Basic tie-breaking: ADSLODs
Before we go any further, we should get straight about what an ADSLOD is. Firstly, like ReDPOTIC, it's another brutally long initialism for a brutally tough-to-name concept of the coinciding-damage method! Secondly, though, it's short for "abbreviated descending-sorted list of damage". Let's work up to that initialism bit by bit.
The "LOD" part is easy: these are "lists of damage". Specifically, they're our target-interval damage lists, which we notate as [math]\displaystyle{ \mathbf{d} }[/math]. (The reversal of "damage list" to "list of damage" is just to make acronym pronounceable. Sorry.)
Next, they are "DS", for "descending-sorted". Note that sorting them causes us to lose track of which target-interval that each damage in the list corresponds to. But that's okay; that information is not important for narrowing down to our optimum tuning. All of our target-intervals are treated equally at this level of the method (we may have weighted their absolute errors differently to obtain our damage, but that's not important here).
This descending-sorting can be thought of as a logical continuation of how we compared the max damage at each tuning. The first entry of each ADSLOD is the max damage done to any interval by that tuning. The second entry of each ADSLOD is the second-most max damage done to any interval by that tuning (which may be the same as the max damage, or less). The third entry is the third-most max damage. And so on.
So in basic tie-breaking, we can compare all the second entries of these ADSLODs to decide which tuning to prefer. And if that doesn't work, then we'll compare all the third entries. And so on. Until we run out of ADSLOD.
Which brings us finally, to the "A" part of the initialism, for "abbreviated". Specifically, we only keep the first [math]\displaystyle{ r + 1 }[/math] entries in these lists, and throw out the rest. This is where [math]\displaystyle{ r }[/math] is the rank of the temperament, or in other words, the count of generators it has. Again, this is the dimension of the tuning damage space we're searching, and so its the number of points required to specify a point within it.
Critically, for our purposes here, that means it's the maximum number of target-intervals we could possibly have minimaxed damage to at this time; if we look any further down this list, then we can't guarantee that the damage values we're looking at are as low as they could possibly be at their position in the list. That's why if these ADSLODs are identical all the way down, we need to try something else, in a new tuning damage space.
We'll learn about this in the advanced tie-breaking section later on.
Basic tie-breaking example: Using the ADSLODs
So, the maximum damages in each damage list weren't enough to choose a tuning. Three of them were tied. We're going to need to look at these three tunings in more detail. Here's our table again, reworked some more, so we only compare the three tied minimax tunings [math]\displaystyle{ 𝒈_1 }[/math], [math]\displaystyle{ 𝒈_2 }[/math], and [math]\displaystyle{ 𝒈_{12} }[/math], and so we show their whole ADSLODs now:
| candidate generator tuning map | target-interval damage list | ADSLOD | |
|---|---|---|---|
| [math]\displaystyle{ 𝒈_i }[/math] | {[math]\displaystyle{ g_1 }[/math] [math]\displaystyle{ g_2 }[/math]] | [math]\displaystyle{ \textbf{d} }[/math] | [math]\displaystyle{ \text{sort}_\text{dsc}(\textbf{d})_{1 \ldots r+1} }[/math] |
| [math]\displaystyle{ 𝒈_1 }[/math] | {238.612 2793.250] | [6.940 6.940 6.940 6.940] | [6.940 6.940 6.940] |
| [math]\displaystyle{ 𝒈_2 }[/math] | {238.612 2779.370] | [6.940 6.940 6.940 6.940] | [6.940 6.940 6.940] |
| [math]\displaystyle{ 𝒈_{12} }[/math] | {238.612 2786.310] | [6.940 6.940 0.000 0.000] | [6.940 6.940 0.000] |
By comparing maximum damages between these candidate tunings already, we've already checked the first entries in each of these ADSLODs. So we start with the second column. Can we tie-break here? No. We've got 6.940, 6.940, and 6.940, respectively. Another three-way tie. Though we've noted that in ADSLODs it no longer matters to which target-intervals the damages are dealt, it may still be understanding-confirming to think through which target-intervals these damages must be for. Well, these first two 6.940 entries must be for the coinciding blue and yellow damages above, the blue/yellow crease, that is, where the damage to [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math] is the same.
Well, one last chance to tie-break before we may need to fall back to advanced tie-breaking. Can we break the tie using the third entries of these ADSLODs. Why, yes! We can! Phew. While [math]\displaystyle{ 𝒈_1 }[/math] and [math]\displaystyle{ 𝒈_2 }[/math] are still tied for 6.940 even in the third position, with [math]\displaystyle{ 𝒈_{12} }[/math] we get by with only 0.000. This could be thought of as corresponding either to the damage for [math]\displaystyle{ \frac51 }[/math] or for [math]\displaystyle{ \frac65 }[/math]. It doesn't matter which one. At [math]\displaystyle{ 𝒈_1 }[/math] and [math]\displaystyle{ 𝒈_2 }[/math] the damage one or both of these two other target-intervals has gotten so big that it's just surpassing that of the damage to [math]\displaystyle{ \frac21 }[/math] and [math]\displaystyle{ \frac31 }[/math] (that's why these are the bounds of the minimax range). But at [math]\displaystyle{ 𝒈_{12} }[/math] one or both of them (we know it's both) is zero.
Note that we refer to equal damages between tunings as "ties"; this is where we have a contest. We are careful to refer to equal damages within tunings as "coinciding", which does double-duty at representing equality and intersection of the target-interval damage graphs.
Thus concludes our demonstration of basic tie-breaking.
When basic tie-breaking fails
We can modify just one thing about our example here in order to cause the basic tie-breaking to fail. Can you guess what it is? We'll give you a moment to pause the article and think. (Haha.)
The answer is: we would only need to remove [math]\displaystyle{ \frac65 }[/math] from our target-interval set. Thus, we'd be finding the {2/1, 3/1, 5/1} minimax-U tuning of blackwood, or more succinctly, its primes minimax-U tuning.[note 21]
And why does basic tie-breaking fail without [math]\displaystyle{ \frac65 }[/math] in the set? This question is perhaps best answered by looking at the from-below view on tuning damage space. But for completeness, let's take a gander at the from-above view first, too.
This looks pretty much the same as before. It's just that there's no red hyper-V damage graph for [math]\displaystyle{ \frac65 }[/math] slicing through here anymore. But it's actually the same exact tied minimax range still.
So what can we see from below, then?
Ah, so there's the same dashed white line as before for the same basic minimax tied range on the other side. But do you notice what's different? Without the red hyper-V graph for [math]\displaystyle{ \frac65 }[/math] anymore, we have no crease coming through to cross the green crease at that magic point we care about! So, this point and its [6.940 6.940 0.000] ADSLOD never comes up for consideration. And so when we get to the step where we compare ADSLODs, we'd only have the two that completely tie with [6.940 6.940 6.940], and get stuck. We would have needed a second crease along the floor to intersect, to cause the method to identify it as a point of interest.
Remember, this coinciding-damage method is only designed to gather points, specifically by checking all the possible places where enough of these damage graphs intersect at once in order to define a point. In 3D tuning damage space we need two creases to intersect at once along the floor to define a point. But here on the floor we've just got one graph, with its crease's line going one direction, and up above we've got two graphs meeting at a different crease, their line going the perpendicular direction. There is a tuning, i.e. a vertical line through tuning damage space, which both of these lines pass through, and that's the tuning we want, the true optimum tuning. But because these lines don't actually cross at a point in tuning damage space, one just passes right over the other, the method misses it.
While we as human observers can pick out right away that what we want is the tuning at that vertical line where the one crease passes over the other, in terms of design of the computer algorithm this method uses, it turns out to be more efficient overall to design it in a way such that it reaches that conclusion another way. And that's what we're going to look at next; that's the advanced tie-breaking.
As a sneak preview, the way the computer will do it is to take the cross-section of tuning damage space wherever that tied range occurs, and gather a new set of coinciding-damage points. From its cross-section view, a 2D tuning damage graph, the blue and yellow graphs will look like horizontal lines, and the green graph will look like a V underneath it. From that view, it will be obvious that the tip of this green V, where the damage to [math]\displaystyle{ \frac51 }[/math] is zero, will be the true optimum tuning. Something like this:
Advanced tie-breaking: Intro
So: comparing ADSLODs (abbreviated descending-sorted list of damages) is not always sufficient to identify a unique optimum tuning. Basic tie-breaking is insufficient whenever more than one coinciding-damage point has the same exact ADSLOD, and these identical ADSLODs also happen to be the best ones insofar as they give a nested minimax tuning, where by "nested minimax" we mean that the maximum damages in each position of these descending-sorted list are minimized, at least as far down the descending-sorted damage list as they've been abbreviated. We might call these "TiNMADSLODs": tied nested minimax abbreviated descending-sorted lists of damage.
In such situations, what we need to do is gather a new set of points, for a new coinciding-damage point set. But it's not like we're starting over from scratch here; it just means that we need to perform another iteration of the same process, but this time searching for tunings in a more focused region of our tuning damage space. In other words, we didn't waste our time or effort; we did make progress with our first coinciding-damage point set. The tunings with TiNMADSLODs which we identified in the previous iteration are valuable: they're what we need to proceed. What these tell us, essentially, is that the true optimum tuning must be somewhere in between them. Our tie indicates not simply two, three, or any finite number of tied tunings; it indicates a continuous range of tunings which all satisfy this tie. The trick now is to define what range, or region, that we mean exactly by "in between", and describe it mathematically. But even more importantly, we've got to figure out how to narrow down the smaller (but still infinite!) set of tuning points within this region to a new set of candidate true optimum tunings.
A slightly oversimplified way to describe this type of tie-breaking would be: whenever we find a range of tunings tied for minimax damage, in order to tie-break within this range, we temporarily ignore the target-intervals in the set which received the actual minimaxed damage amount, then search this range for the tuning that minimizes the otherwise maximum damage. And we just keep repeating this process until we finally identify a single true optimum tuning.
Advanced tie-breaking example: Setup
To help illustrate advanced tie-breaking, we're going to look at a minimax-C tuning of augmented temperament, with mapping [⟨3 0 7] ⟨0 1 0]}. In particular, we're going to use the somewhat arbitrary target-interval set [math]\displaystyle{ \{ \frac32, \frac52, \frac53, \frac83, \frac95, \frac{16}{5}, \frac{15}{8}, \frac{18}{5} \} }[/math]. As a rank-2 temperament, we're going to be searching 3D tuning damage space. This temperament divides the octave into three parts, so our ballpark [math]\displaystyle{ g_1 }[/math] is 400 ¢, and our second generator [math]\displaystyle{ g_2 }[/math] is a free generator for prime 3, so it's going to be ballpark its pure tuning of 1901.955 ¢.
Here's an aerial view on the tuning damage space, where we've "clipped" every damage graph hyper-V where it has gone out-of-bounds, above 150 ¢(C) damage; that is, we've colored it in grey and flattened it across the top of the box of our visualization. This lets us focus in clearly on the region of real interest, which is where all target-intervals' damages are less than this cap at the same time. This is the multicolored crater in the middle here:
Like the blackwood example we looked at in the basic tie-breaking section, this max damage graph also ends up with a line segment region on top that's exactly parallel to the floor, therefore every tuning along this range is tied for minimax. This happens to be 92.557 ¢(C) damage.
(Again, this was made possible by the prime compositions of our target-intervals, and how this temperament maps them. Specifically, the yellow graph here is [math]\displaystyle{ \frac{15}{8} }[/math] and the blue graph is [math]\displaystyle{ \frac{18}{5} }[/math]. The first interval [math]\displaystyle{ \frac{18}{5} }[/math] is one augmented comma [math]\displaystyle{ \frac{128}{125} }[/math] off from [math]\displaystyle{ (\frac{15}{8})^2 = \frac{225}{64} }[/math]. In vector form, we have [1 2 -1⟩ = 2×[-3 1 1⟩ - [-7 0 3⟩). So since [math]\displaystyle{ \frac{15}{8} }[/math] maps to [-2 1}, that means that [math]\displaystyle{ \frac{18}{5} }[/math] maps to [-4 2}. And since [-4 2} = 2×[-2 1}, i.e. a simple scalar relates these two mapped intervals. In other words, they have the same proportion of generators, this means their damage graph creases will be parallel.)
Every tuning along this range is tied for second-most minimax, still 92.557 ¢(C), on account of it being a crease between two target-interval damage graphs. But we can look 3 positions down the ADSLODs here on account of it being a rank-2 ([math]\displaystyle{ r = 2 }[/math]) temperament and so tuning damage space is [math]\displaystyle{ (r + 1 = 3) }[/math]-dimensional. But this doesn't help us. Because the reason this line segment range ends at the endpoints it ends at is because that's exactly where some third damage graph finally shoots higher above 92.557 ¢(C). So the third entries in the these ADSLODs are also tied for 92.557 ¢(C).
And here's the key issue: this augmented example is more like the variation we briefly looked at for blackwood, where basic tie-breaking failed us, on account of there not happening to be any other identifiable points of interest immediately below the minimax line segment. Below this line segment, then, there must be only sloping planes, or possibly some other creases, but no points. So in order to nested minimax further, we'll have to create some points below it, by taking a cross-section right along that tied range, and seeing which damage graph V's we can find to intersect in that newly focused 2D tuning damage space.
The two tied minimax tunings we've identified are {399.809 1901.289] and {400.865 1903.401]. So, we're already very close to an answer: our [math]\displaystyle{ g_1 }[/math] has been narrowed down almost to the range of a single cent, while our [math]\displaystyle{ g_2 }[/math] is narrowed down almost to the range of two cents.
And here's what that cross-section looks like.
(Sorry for the changed colors of the graphs. Not enough time to nudge Wolfram Language into being nice.)
For now, don't worry too much about the horizontal axis, but know that the range from 0.0 to 1.0 is our actual tied minimax range. It's a little tricky to label this axis. It's not as simple as it was when we showed the cross-section for blackwood, because that cross-section was parallel to one of the generator axes, so we could simply label it with that generator's sizes. But this cross-section is diagonal through our tuning damage space (from above), so no such luck! (Well, we chose an example like this by design, to show how the method grapples with tricky situations like this. We'll get to it soon enough.)
We can see that 0.0 and 1.0 are the points where another damage graph crosses above the horizontal line otherwise on top, the horizontal line which corresponds to the crease between the damage graphs for [math]\displaystyle{ \frac{15}{8} }[/math] and [math]\displaystyle{ \frac{18}{5} }[/math], which appears as brown here. So those two target-intervals which cause the range to end at either end are [math]\displaystyle{ \frac{16}{5} }[/math] and [math]\displaystyle{ \frac95 }[/math].
These two target-intervals [math]\displaystyle{ \frac{16}{5} }[/math] and [math]\displaystyle{ \frac95 }[/math] also happen to be the two target-intervals whose crossing is going to yield us the point we need to identify the true optimum tuning! We can see that if we pretend that the horizontal [math]\displaystyle{ \frac{15}{8} }[/math] and [math]\displaystyle{ \frac{18}{5} }[/math] aren't here, and then just gather all the points in this view where target-intervals cross or bounce off the zero-damage floor as normal (that's our second iteration of the method, gathering another round of coinciding-damage points!), and check the maximum damages at each of those tunings, and then choose the tuning with the lowest maximum damage (possibly involving basic tie-breaking with ADSLODs, though we won't need it in this particular case), we're going to find that point where [math]\displaystyle{ \frac{16}{5} }[/math] and [math]\displaystyle{ \frac95 }[/math] cross. To be clear, those are the yellow and blue graphs here, and they cross about a third of the way from 0.0 to 1.0.
Spoiler alert: the tuning this crossing identifies is {400.171 1902.011], which as it should be is somewhere between our previously tied tunings of {399.809 1901.289] and {400.865 1903.401]. This is indeed our true optimum tuning. But in order to understand how we would determine these exact cents values from this cross-sectioning process, we're going to have to take a little detour. In order to understand how these further iterations of the coinciding-damage method work, we need to understand the concept of blends.
Blends: Abstract concept
Let's begin to learn blends in the abstract (though you may well try to guess ahead as to the application of these concepts to the RTT problem at hand).
Suppose we want a good way to describe a line segment between two other points [math]\displaystyle{ \mathbf{A} }[/math] and [math]\displaystyle{ \mathbf{B} }[/math], or in other words, any point between these two points. We could describe this arbitrary point [math]\displaystyle{ \mathbf{P} }[/math] as some blend of point [math]\displaystyle{ \mathbf{A} }[/math] and point [math]\displaystyle{ \mathbf{B} }[/math], like this: [math]\displaystyle{ \mathbf{P} = x\mathbf{A} + y\mathbf{B} }[/math], where [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are our blending variables.
For example, if [math]\displaystyle{ x=1 }[/math] and [math]\displaystyle{ y=0 }[/math], then [math]\displaystyle{ \mathbf{P} = (1)\mathbf{A} + (0)\mathbf{B} = \mathbf{A} }[/math]. And if [math]\displaystyle{ x=0 }[/math] and [math]\displaystyle{ y=1 }[/math], then similarly [math]\displaystyle{ \mathbf{P} = \mathbf{B} }[/math]. Now if both [math]\displaystyle{ x=0 }[/math] and [math]\displaystyle{ y=0 }[/math], we might say [math]\displaystyle{ \mathbf{P} = \mathbf{O} }[/math], where this point [math]\displaystyle{ \mathbf{O} }[/math] is our origin, out there in space somewhere; however, if we want to use this technique in a useful way, we don't actually need to worry about this origin, because in turns out that if we simply require that [math]\displaystyle{ x+y=1 }[/math], we can ensure that we can only reach points along that line segment connecting [math]\displaystyle{ \mathbf{A} }[/math] to [math]\displaystyle{ \mathbf{B} }[/math]! For example, with [math]\displaystyle{ x = \frac12 }[/math] and [math]\displaystyle{ y = \frac12 }[/math], we describe the point exactly halfway between [math]\displaystyle{ \mathbf{A} }[/math] and [math]\displaystyle{ \mathbf{B} }[/math].
We can generalize this idea to higher dimensions. That was the 1-dimensional case. Suppose instead we have three points: [math]\displaystyle{ \mathbf{A} }[/math], [math]\displaystyle{ \mathbf{B} }[/math], and [math]\displaystyle{ \mathbf{C} }[/math]. Now the region bounded by these points is no longer a 1D line segment. It's a 2D plane segment. Specifically, it's a triangle, with points at our three points. And now our point [math]\displaystyle{ \mathbf{P} }[/math] that is somewhere inside this triangle can be described as [math]\displaystyle{ \mathbf{P} = x\mathbf{A} + y\mathbf{B} + z\mathbf{C} }[/math], where now [math]\displaystyle{ x + y + z = 1 }[/math].
And so on to higher and higher dimensions.
One fewer blending variable; anchor
However, let's pause at the 2-dimensional case to make an important observation: we don't actually need one blending variable for each point being blended. In practice, since our blending variables are required to sum to 1, we only really need one fewer blending variable than we have points. When [math]\displaystyle{ x + y + z = 1 }[/math], then we know [math]\displaystyle{ x }[/math] must equal [math]\displaystyle{ 1 - y - z }[/math], so that:
[math]\displaystyle{
\begin{align}
x + y + z &= 1
(1 - y - z) + y + z &= 1
1 - \cancel{y} - \cancel{z} + \cancel{y} + \cancel{z} &= 1
1 &= 1
\end{align}
}[/math]
But how would we modify our [math]\displaystyle{ \mathbf{P} = x\mathbf{A} + y\mathbf{B} + z\mathbf{C} }[/math] formula to account for this unnecessity of [math]\displaystyle{ x }[/math]?
We note that the choice of [math]\displaystyle{ x }[/math]—and therefore [math]\displaystyle{ \mathbf{A} }[/math]—was arbitrary; we simply felt that picking the first blending variable and point would be simplest, and provide the convenience of consistency when examples from different dimensions were compared.
Clearly we can't simply drop [math]\displaystyle{ x }[/math] with no further modifications; in that case, we'd have [math]\displaystyle{ \mathbf{P} = \mathbf{A} + y\mathbf{B} + z\mathbf{C} }[/math], so now every single point is going to essentially have [math]\displaystyle{ x = 1 }[/math], or in other words, a whole [math]\displaystyle{ \mathbf{A} }[/math] mixed in.
Well, the key is to change what [math]\displaystyle{ y }[/math] and [math]\displaystyle{ z }[/math] blend in. Think of it this way: if we always have a full [math]\displaystyle{ \mathbf{A} }[/math] mixed in to our [math]\displaystyle{ \mathbf{P} }[/math], then all we need to worry about are the deviations from this [math]\displaystyle{ \mathbf{A} }[/math]. That is, we need the formula like so:
[math]\displaystyle{
\mathbf{P} = \mathbf{A} + y(\mathbf{B} - \mathbf{A}) + z(\mathbf{C} - \mathbf{A})
}[/math]
So now when [math]\displaystyle{ y=1 }[/math] and [math]\displaystyle{ z=0 }[/math], we still find [math]\displaystyle{ \mathbf{P} = \mathbf{B} }[/math] as before:
[math]\displaystyle{
\mathbf{P} = \mathbf{A} + y(\mathbf{B} - \mathbf{A}) + z(\mathbf{C} - \mathbf{A})
\mathbf{P} = \mathbf{A} + (1)(\mathbf{B} - \mathbf{A}) + (0)(\mathbf{C} - \mathbf{A})
\mathbf{P} = \mathbf{A} + \mathbf{B} - \mathbf{A}
\mathbf{P} = \mathbf{B}
}[/math]
And similarly [math]\displaystyle{ \mathbf{P} = \mathbf{C} }[/math] for [math]\displaystyle{ y = 0 }[/math] and [math]\displaystyle{ z = 1 }[/math].
For convenience, we could refer to this arbitrary point [math]\displaystyle{ \mathbf{A} }[/math] our anchor'.
For a demonstration of the relationship between the formula with [math]\displaystyle{ \mathbf{A} }[/math] extracted and the original formula, please see #Derivation of extracted anchor.
FYI, the general principle at work with blends here is technically called a "convex combination"; feel free to read more about them now if you're not comfortable with the idea yet.
Combining insights
Okay, and we're almost ready to tie this back to our RTT application. Realize that back in 1D, we'd have
[math]\displaystyle{
\mathbf{P} = \mathbf{A} + y(\mathbf{B} - \mathbf{A})
}[/math]
So now think back to the 2D damage graph for the second coinciding-damage point set we looked at in the augmented temperament example of the previous section. Every tuning damage graph we've ever looked at has had damage as the vertical axis, and every other axis corresponding to the tuning of a generator… except that graph! Recall that we took a cross-section of the original 3D tuning damage space. So the horizontal axis of that graph is not any one of our generators. As we mentioned, it runs diagonally across the zero-damage floor, since the sizes of the two target-intervals which define it depend on the sizes of both these generators.
What is the axis, then, though? Well, one way to put it would be, recalling that we took it as the cross-section between two TiNMADSLOD tunings, would be this: it's a blending variable. It's just like our abstract case, but here, the points we're blending between are tunings. In one direction we increase the blend of the first of these two tunings, and in the other direction we increase the blend of the other tuning. Or, in recognition of the "one fewer" insight, we have one blending variable that controls from 0, not at all, to 1, completely, by how much we blend away from our anchor tuning to the other tuning. We could imagine this is just like our point [math]\displaystyle{ \mathbf{P} }[/math] which is a blend between [math]\displaystyle{ \mathbf{A} }[/math], [math]\displaystyle{ \mathbf{B} }[/math] using blend variables [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math]:
But next, we've got to grow up, and stop using these vague, completely abstract points. We've got to commit to fully applying this blending concept to RTT. Let's start using tuning-related objects now.
Substituting RTT objects in
So we're looking along this line segment for our true optimum tuning, our equivalent of point [math]\displaystyle{ \mathbf{P} }[/math]. Let's call it [math]\displaystyle{ 𝒈 }[/math], simply our generator tuning map.
But our points [math]\displaystyle{ \mathbf{A} }[/math] and [math]\displaystyle{ \mathbf{B} }[/math] are also generator tuning maps. Let's call those [math]\displaystyle{ 𝒈_0 }[/math] and [math]\displaystyle{ 𝒈_1 }[/math], that is, with subscripted indices.
We've zero-indexed these because [math]\displaystyle{ 𝒈_0 }[/math] will be our anchor tuning, and therefore will be to large extent special and outside the normal situation; in particular, it won't need a corresponding blend variable, and it's better if our blend variables can be one-indexed like how we normally index things.
Right, so while the A, B, C and x, y, z thing worked fine for the abstract case, it'll be better moving forward if we use the same variable letter for the same type of thing, and use subscripted indices to distinguish them, so let's replace the blending variable that corresponded to point [math]\displaystyle{ \mathbf{B} }[/math], which was [math]\displaystyle{ y }[/math], with [math]\displaystyle{ b_1 }[/math], since that corresponds with [math]\displaystyle{ 𝒈_1 }[/math], which is what [math]\displaystyle{ \mathbf{B} }[/math] became.
So here's what we've got so far:
[math]\displaystyle{
𝒈 = 𝒈_{0} + b_1(𝒈_{1} - 𝒈_{0})
}[/math]
Generalizing to higher dimensions: The blend map
Now that's the formula for finding a generator tuning map [math]\displaystyle{ 𝒈 }[/math] somewhere in the line segment between two other tied generator tuning maps [math]\displaystyle{ 𝒈_0 }[/math] and [math]\displaystyle{ 𝒈_1 }[/math]. And that would work fine for our augmented temperament example. But before crawl back into the weeds on that example, let's solidify our understanding of the concepts by generalizing them, so we can feel confident we could use them for any advanced tie-breaking situation.
It shouldn't be hard to see that for a 2D triangular case—if we wanted to find a [math]\displaystyle{ 𝒈 }[/math] somewhere in between tied [math]\displaystyle{ 𝒈_0 }[/math], [math]\displaystyle{ 𝒈_1 }[/math], and [math]\displaystyle{ 𝒈_2 }[/math]—we'd use the formula:
[math]\displaystyle{
𝒈 = 𝒈_{0} + b_1(𝒈_{1} - 𝒈_{0}) + b_2(𝒈_{2} - 𝒈_{0})
}[/math]
Each new tied [math]\displaystyle{ 𝒈_i }[/math] adds a new blending variable, which scales its delta with the anchor tuning [math]\displaystyle{ 𝒈_0 }[/math].
We should recognize now that we might have an arbitrarily large number of tied tunings. This is a perfect job for a vector, that is, we should gather up all our [math]\displaystyle{ b_i }[/math] into one object, a vector called [math]\displaystyle{ 𝒃 }[/math].
Well, it is a vector, but in particular its a row vector, or covector, which we more commonly refer to as a map. This shouldn't be terribly surprising that it's a map, because we said a moment ago that while our tuning damage graph's axes (other than the damage axis) usually correspond to generator (tuning map)s, for our second iteration of this method here, in the cross-section view, those axes correspond to blending variables. So in general, the blend map [math]\displaystyle{ 𝒃 }[/math] takes the place of the generator tuning map [math]\displaystyle{ 𝒈 }[/math] in iterations of the coinciding-damage method beyond the first.
The deltas matrix
Here's the full setup, for an arbitrary count of ties:
[math]\displaystyle{
𝒈 =
\begin{array} {c}
\text{anchor tuning} \\
𝒈_{0} \\
\end{array}
+
\begin{array} {c}
\text{blend map} \; 𝒃 \\
\left[ \begin{array} {c}
b_1 & b_2 & \cdots & b_{τ-1}
\end{array} \right] \\
\end{array}
\begin{array} {c}
\text{tuning deltas} \\
\left[ \begin{array} {c}
𝒈_{1} - 𝒈_{0} \\
𝒈_{2} - 𝒈_{0} \\
\vdots \\
𝒈_{τ-1} - 𝒈_{0} \\
\end{array} \right] \\
\end{array}
}[/math]
We're using the variable [math]\displaystyle{ τ }[/math] here for our count of tied tunings. (It's the Greek letter "tau". We're avoiding 't' because "tuning" and "temperament" both already use that letter.)
We'd like a simpler way to refer to the big matrix on the right. As we've noted above, it's a matrix of deltas. In particular, it's a matrix of deltas between the anchor tied tuning and the other tied tunings.
We don't typically see differences between generator tuning maps in RTT. These map differences are cousins to our retuning maps [math]\displaystyle{ 𝒓 }[/math], we suppose, insofar as they're the difference between two tuning maps of some kind, but the comparison ends there, because:
- in the case of a retuning map, one of the maps is just and the other tempered, while in this case both are tempered, and
- in the case of a retuning map, both are prime tuning maps, while in this case both are generator tuning maps.
We can make use of the Greek letter delta and its association with differences. So let's use [math]\displaystyle{ 𝜹_i }[/math] as a substitute for [math]\displaystyle{ 𝒈_i - 𝒈_{0} }[/math]. We may call it a delta of generator tuning maps. The delta [math]\displaystyle{ 𝜹_i }[/math] takes the index [math]\displaystyle{ i }[/math] of whichever tied tuning is the one the anchor tuning is subtracted from. (More payoff for our zero-indexing of those; our deltas here, like our blend map entries, will therefore be one-indexed as per normal.)
Substituting back into our formula, then, we find:
[math]\displaystyle{
𝒈 =
\begin{array} {c}
\text{anchor tuning} \\
𝒈_{0} \\
\end{array}
+
\begin{array} {c}
\text{blend map} \; 𝒃 \\
\left[ \begin{array} {c}
b_1 & b_2 & \cdots & b_{τ-1}
\end{array} \right] \\
\end{array}
\begin{array} {c}
\text{tuning deltas} \\
\left[ \begin{array} {c}
𝜹_1 \\
𝜹_2 \\
\vdots \\
𝜹_{τ-1} \\
\end{array} \right] \\
\end{array}
}[/math]
But we can do a bit better. Let's find a variable that could refer to this whole matrix, whose rows are each generator tuning map deltas. The natural thing seems to be to use the capital version of the Greek letter delta, which is [math]\displaystyle{ \textit{Δ} }[/math]. However, this letter is so strongly associated with use as an operator, for representing the difference in values of the thing just to its right, that probably this isn't the best idea. How about instead we just use the Latin letter [math]\displaystyle{ D }[/math], for "delta". This is our (generator tuning map) deltas matrix.
This lets us simplify the formula down to this:
[math]\displaystyle{
𝒈 = 𝒈_{0} + 𝒃D
}[/math]
How to identify tunings
This formula assumes we already have all of our tied tunings [math]\displaystyle{ 𝒈_0 }[/math] through [math]\displaystyle{ 𝒈_{τ - 1} }[/math] from the previous coinciding-damage point set, i.e. the previous iteration of the algorithm. And so we already know the [math]\displaystyle{ 𝒈_0 }[/math] and [math]\displaystyle{ D }[/math] parts of this equation. This equation, then, gives us a way to find a tuning [math]\displaystyle{ 𝒈 }[/math] given some blend map [math]\displaystyle{ 𝒃 }[/math]. But what we really want to do is identify not just any tunings that are such blends, but particular tunings that are such blends: we want to find the ones that are part of the next iteration's coinciding-damage point set, the ones where damage graphs intersect in our cross-sectional diagram.
We can accomplish this by solving for each [math]\displaystyle{ 𝒃 }[/math] with respect to a given constraint matrix [math]\displaystyle{ K }[/math]. This is just as we solved for each [math]\displaystyle{ 𝒈 }[/math] in the first iteration with respect to each [math]\displaystyle{ K }[/math]; again, [math]\displaystyle{ 𝒃 }[/math] is filling the role of [math]\displaystyle{ 𝒈 }[/math] here now.
So we've got our [math]\displaystyle{ 𝒕\mathrm{T}WK = 𝒋\mathrm{T}WK }[/math] setup. Remember that in the first iteration, [math]\displaystyle{ K }[/math] had [math]\displaystyle{ r }[/math] columns, one for each generator to solve for, since each column corresponds to an unchanged-interval of the tuning. In other words, one column of [math]\displaystyle{ K }[/math] for each entry of [math]\displaystyle{ 𝒈 }[/math]. Well, so we're still going to use constraint matrices to identify tunings here, but now they're going to have [math]\displaystyle{ τ - 1 }[/math] columns, one for each entry in the blend map, which has one entry for each delta of a tied tuning past the anchor tied tuning (a delta with the anchor tied tuning). We can still use the symbol [math]\displaystyle{ K }[/math] for these constraint matrices, even though it's a somewhat different sort of constraint, with a different shape [math]\displaystyle{ (k, τ -1) }[/math].
Next, let's just unpack [math]\displaystyle{ 𝒕 }[/math] to [math]\displaystyle{ 𝒈M }[/math]:
[math]\displaystyle{
𝒈M\mathrm{T}WK = 𝒋\mathrm{T}WK
}[/math]
And substitute [math]\displaystyle{ 𝒈_{0} + 𝒃D }[/math] in for [math]\displaystyle{ 𝒈 }[/math]:
[math]\displaystyle{
(𝒈_{0} + 𝒃D)M\mathrm{T}WK = 𝒋\mathrm{T}WK
}[/math]
Distribute:
[math]\displaystyle{
𝒈_{0}M\mathrm{T}WK + 𝒃DM\mathrm{T}WK = 𝒋\mathrm{T}WK
}[/math]
Work toward isolating [math]\displaystyle{ 𝒃 }[/math].
[math]\displaystyle{
𝒃DM\mathrm{T}WK = 𝒋\mathrm{T}WK - 𝒈_{0}M\mathrm{T}WK
}[/math]
Group on the right-hand side:
[math]\displaystyle{
𝒃DM\mathrm{T}WK = (𝒋 - 𝒈_{0}M)\mathrm{T}WK
}[/math]
Replace [math]\displaystyle{ 𝒈_{0}M }[/math] with [math]\displaystyle{ 𝒕_0 }[/math] which is the corresponding (prime) tuning map to [math]\displaystyle{ 𝒈_{0} }[/math].
[math]\displaystyle{
𝒃DM\mathrm{T}WK = (𝒋 - 𝒕_0)\mathrm{T}WK
}[/math]
We normally see the just tuning map subtracted from the tempered tuning map, not the other way around as we have here. So let's just negate everything. This is no big deal, since [math]\displaystyle{ 𝒃 }[/math] is an unknown variable after all, so we can essentially think of this [math]\displaystyle{ 𝒃 }[/math] as a new [math]\displaystyle{ 𝒃 }[/math] equal to the negation of our old [math]\displaystyle{ 𝒃 }[/math].
[math]\displaystyle{
𝒃DM\mathrm{T}WK = (𝒕_0 - 𝒋)\mathrm{T}WK
}[/math]
So that's just a (prime) retuning map on the right:
[math]\displaystyle{
𝒃DM\mathrm{T}WK = 𝒓_{0}\mathrm{T}WK
}[/math]
We've now reached the point where Keenan's original version of this algorithm would solve directly for [math]\displaystyle{ 𝒃 }[/math], analogous to how it solves directly (and approximately) for [math]\displaystyle{ 𝒈 }[/math] in the first iteration. But when we use the matrix inverse technique—where instead of solving directly (and approximately) for a generator tuning map [math]\displaystyle{ 𝒈 }[/math] we instead solve exactly for a generator embedding [math]\displaystyle{ G }[/math] and can then later obtain [math]\displaystyle{ 𝒈 }[/math] as [math]\displaystyle{ 𝒈 = 𝒋G }[/math]—then here we must be solving exactly for some matrix which we could call [math]\displaystyle{ B }[/math], following the analogy [math]\displaystyle{ 𝒈 : G :: 𝒃 : B }[/math]. (Not to be confused with the subscripted [math]\displaystyle{ B_s }[/math] that we use for basis matrices; these two matrices will probably never meet, though). This will be a [math]\displaystyle{ (d, τ-1) }[/math]-shaped matrix, which we could call the blend matrix.
And this is why we noted the thing earlier about how constraint matrices are about identifying tunings, not optimizing them. If you come across this setup, and see that somehow, for some reason, [math]\displaystyle{ 𝒓_0 }[/math] has replaced [math]\displaystyle{ 𝒋 }[/math], you might want to try to answer the question: why are we trying to optimize things relative to some arbitrary retuning map, now, instead of JI? The problem with that is: it's the wrong question. It's not so much that [math]\displaystyle{ 𝒓_0 }[/math] is a goal or even a central player in this situation. It just sort of works out this way.
It turns out that while [math]\displaystyle{ 𝒋 }[/math] is what relates [math]\displaystyle{ G }[/math] to [math]\displaystyle{ 𝒈 }[/math], it's [math]\displaystyle{ 𝒓_0 }[/math] which relates this [math]\displaystyle{ B }[/math] to [math]\displaystyle{ 𝒃 }[/math]. This shouldn't be hugely surprising, since [math]\displaystyle{ 𝒓_0 }[/math] is sort of "filling the role" of [math]\displaystyle{ 𝒋 }[/math] there on the right-hand side, insofar as it finds itself in the same position as [math]\displaystyle{ 𝒋 }[/math] did in the simpler case.
So we get:
[math]\displaystyle{
𝒓_{0}BDM\mathrm{T}WK = 𝒓_{0}\mathrm{T}WK
}[/math]
And cancel out the [math]\displaystyle{ 𝒓_0 }[/math] on both sides:
[math]\displaystyle{
\begin{align}
\cancel{𝒓_{0}}BDM\mathrm{T}WK &= \cancel{𝒓_{0}}\mathrm{T}WK \\
BDM\mathrm{T}WK &= \mathrm{T}WK
\end{align}
}[/math]
Then we do our inverse. This is the exact analog of [math]\displaystyle{ G = \mathrm{T}WK(M\mathrm{T}W)^{-1} }[/math]:
[math]\displaystyle{
B = \mathrm{T}WK(DM\mathrm{T}WK)^{-1}
}[/math]
And once we have that, adapting our earlier formula for [math]\displaystyle{ 𝒈 }[/math] from [math]\displaystyle{ 𝒃 }[/math] to give us [math]\displaystyle{ 𝒈 }[/math] from [math]\displaystyle{ B }[/math] instead:
[math]\displaystyle{
𝒈 = 𝒈_{0} + 𝒓_{0}BD
}[/math]
So all in one formula, substituting our formula for [math]\displaystyle{ B }[/math] into that, we have:
[math]\displaystyle{
𝒈 = 𝒈_{0} + 𝒓_{0}\mathrm{T}WK(DM\mathrm{T}WK)^{-1}D
}[/math]
And that's how you find the generators for a tuning corresponding to a coinciding damage point described by [math]\displaystyle{ K }[/math] at whichever point in a tied minimax tuning range it lays.
Computing damage
We could compute the damage list from any [math]\displaystyle{ 𝒈 }[/math], as normal: [math]\displaystyle{ 𝐝 = |𝐞|W = |𝒓\mathrm{T}|W = |(𝒕 - 𝒋)\mathrm{T}|W = |(𝒈M - 𝒋)\mathrm{T}|W }[/math]. But actually we don't have to recover [math]\displaystyle{ 𝒈 }[/math] from [math]\displaystyle{ B }[/math] in order to compute damage. There's a more expedient way to compute it. If:
[math]\displaystyle{
𝒃DM\mathrm{T}WK = 𝒓_{0}\mathrm{T}WK
}[/math]
then pulling away the constraint, we revert from an equality to an approximation:
[math]\displaystyle{
𝒃DM\mathrm{T}W ≈ 𝒓_{0}TW
}[/math]
And the analogous thing we minimize to make this approximation close (review the basic algebraic setup if need be) would be:
[math]\displaystyle{
|(𝒃DM - 𝒓_{0})\mathrm{T}|W
}[/math]
So the damage caused by a blend map [math]\displaystyle{ 𝒃 }[/math] is:
In other words, we can find it using the same formula as we normally use, [math]\displaystyle{ |(𝒈M - 𝒋)\mathrm{T}|W }[/math], but using [math]\displaystyle{ 𝒃 }[/math] instead of [math]\displaystyle{ 𝒈 }[/math], [math]\displaystyle{ DM }[/math] instead of [math]\displaystyle{ M }[/math], and [math]\displaystyle{ 𝒓_0 }[/math] instead of [math]\displaystyle{ 𝒋 }[/math]. Which is just what we end up with upon substituting [math]\displaystyle{ 𝒈_0 + 𝒃D }[/math] in for [math]\displaystyle{ 𝒈 }[/math]:
[math]\displaystyle{
|((𝒈_{0} + 𝒃D)M - 𝒋)\mathrm{T}|W
|(𝒈_{0}M + 𝒃DM - 𝒋)\mathrm{T}|W
|(𝒕_{0} + 𝒃DM - 𝒋)\mathrm{T}|W
|(𝒃DM - 𝒓_{0})\mathrm{T}|W
}[/math]
Blends of blends
Okay then. So if we find the blend for each point of our next iteration's coinciding-damage point set, and use that to find the damage for that blend, then hopefully this time we find a unique minimax as far down the lists as we can validly compare.
And if not, we rinse and repeat. Which is to say, where here our generators are expressed in terms of a blend of other tunings, after another iteration of continued searching, our generators would be expressed as a blend of other tunings, where each blend was itself a blend of other tunings. And so on.
Apply formula to example
To solidify our understanding, let's finally return to that real-life augmented example, and apply the concepts we learned to it!
At the point our basic tie-breaking failed, we found two tied tunings. Let the first one be our anchor tuning, [math]\displaystyle{ 𝒈_0 }[/math], and the second be our [math]\displaystyle{ 𝒈_1 }[/math]:
[math]\displaystyle{
𝒈_0 = \left[ \begin{array} {r} 399.809 & 1901.289 \end{array} \right] \\
𝒈_1 = \left[ \begin{array} {r} 400.865 & 1903.401 \end{array} \right] \\
}[/math]
Let me drop the cross-section diagram here again, for conveniently close reference, and with some smarter stuff on top of it this time:
So our prediction looks like it should be about [math]\displaystyle{ b_1 = 0.35 }[/math] in order to nail that point we identified earlier where the red and olive lines cross at the triangle underneath the flat tie line across the top.
And here's the formula again for a tuning here from [math]\displaystyle{ K }[/math], again, for conveniently close reference:
[math]\displaystyle{
B = \mathrm{T}WK(DM\mathrm{T}WK)^{-1}
}[/math]
Let's get easy stuff out of the way first. We know [math]\displaystyle{ M }[/math] = [⟨3 0 7] ⟨0 1 0]}. As for [math]\displaystyle{ \mathrm{T} }[/math], in the beginning we gave it as [math]\displaystyle{ \{ \frac32, \frac52, \frac53, \frac83, \frac95, \frac{16}{5}, \frac{15}{8}, \frac{18}{5} \} }[/math]. And [math]\displaystyle{ W }[/math] will just be the diagonal matrix of their log-product complexities, since we went with minimax-C tuning here.
Okay, how about [math]\displaystyle{ K }[/math] next then. Since [math]\displaystyle{ τ = 2 }[/math] here—we have two tied tunings—we know [math]\displaystyle{ K }[/math] will have only [math]\displaystyle{ τ - 1 = 1 }[/math] column. And [math]\displaystyle{ k = 8 }[/math], so that's its row count. In particular, we're looking for the tuning where [math]\displaystyle{ \frac95 }[/math] and [math]\displaystyle{ \frac{16}{5} }[/math] have exactly equal errors, i.e. they even have the same sign, not opposite signs[note 22]. So to get them to cancel out, we use a -1 as the nonzero entry of one of the two intervals, and conventionally we use 1 for the first one. So with [math]\displaystyle{ \frac95 }[/math] at index 5 of [math]\displaystyle{ \mathrm{T} }[/math] and [math]\displaystyle{ \frac{16}{5} }[/math] at index 6, we find [math]\displaystyle{ K }[/math] = [0 0 0 0 1 -1 0 0].
Now for [math]\displaystyle{ D }[/math]. We know it's a [math]\displaystyle{ (τ - 1, 𝑟) }[/math]-shaped matrix: one row for each tied tuning past the first, and each row is the delta between generator tuning maps, so is [math]\displaystyle{ r }[/math] long like any generator tuning map. In our case we have [math]\displaystyle{ τ = 2 }[/math] and [math]\displaystyle{ r = 2 }[/math], so it's a [math]\displaystyle{ (1,2) }[/math]-shaped matrix. That one row is [math]\displaystyle{ 𝒈_1 - 𝒈_0 }[/math]. So it's {400.865 1903.401] - {399.809 1901.289] = {1.056 2.112].
And that's everything we need to solve!
Work that out and we get [math]\displaystyle{ B }[/math] = [[-0.497891 -0.216260 -0.016343⟩]. (We're showing a little extra precision here than usual.) So we can recover [math]\displaystyle{ 𝒈 }[/math] now as:
[math]\displaystyle{
𝒈 = 𝒈_0 + 𝒓_{0}BD
}[/math]
We haven't worked out [math]\displaystyle{ 𝒓_0 }[/math] yet, but it's [math]\displaystyle{ 𝒕_0 - 𝒋 }[/math], where [math]\displaystyle{ 𝒋 }[/math] = ⟨1200.000 1901.955 2786.314] and [math]\displaystyle{ 𝒕_0 = 𝒈_{0}M }[/math] = {399.809 1901.289][⟨3 0 7] ⟨0 1 0]} = ⟨1199.43 1901.29 2798.66], so [math]\displaystyle{ 𝒓_0 }[/math] = ⟨0.573 0.666 12.349].
Plugging everything in at once could be unwieldy. So let's just do the [math]\displaystyle{ 𝒓_{0}B }[/math] part to find [math]\displaystyle{ 𝒃 }[/math]. We might be curious about that anyway… how close does it match our prediction of about 0.35? Well, it's ⟨0.573 0.666 12.349][[-0.497891 -0.216260 -0.016343⟩] = 0.343. Not bad!
So now plug [math]\displaystyle{ 𝒃 }[/math] into [math]\displaystyle{ 𝒈 = 𝒈_0 + 𝒃D }[/math] and we find [math]\displaystyle{ 𝒈 }[/math] = {399.809 1901.289] + 0.343×{1.056 2.112] = {400.171 1902.011]. And that's what we were looking for!
The ADSLOD here, by the way, is [92.557 92.557 81.117 81.117 57.928 ... ] So it's a tie of 81.117 ¢(C) for the second-most minimax damage to [math]\displaystyle{ \frac95 }[/math] and [math]\displaystyle{ \frac{16}{5} }[/math]. No other tuning can beat this 81.117 number, even just three entries down the list. And so we're done.
Exact solutions with advanced tie-breaking
As for recovering [math]\displaystyle{ G }[/math], though. You know, the whole point of this article—finding exact tunings—we wouldn't want to give up on that just because we had to use advanced tie-breaking, would we?
So we've been looking for [math]\displaystyle{ 𝒈 }[/math] which are blends of other [math]\displaystyle{ 𝒈 }[/math]'s. But we need to look for [math]\displaystyle{ G }[/math]'s that are blends of other [math]\displaystyle{ G }[/math]'s! Doing that directly would explode the dimensionality of the space we're searching, by the rank [math]\displaystyle{ r }[/math] times the length of the blend vector [math]\displaystyle{ 𝒃 }[/math], that is, [math]\displaystyle{ 𝑟×(τ - 1) }[/math]. And would it even be meaningful to independently search the powers of the primes that comprise each entry of a [math]\displaystyle{ 𝒈 }[/math]? Probably not. The compressed information in [math]\displaystyle{ 𝒈 }[/math] is all that really matters for defining the constrained search region. So what if instead we still search by [math]\displaystyle{ 𝒈 }[/math], but what if the blend we find for each [math]\displaystyle{ K }[/math] can be applied to [math]\displaystyle{ G }[/math]'s instead of [math]\displaystyle{ 𝒈 }[/math]'s?
Let's test on an example.
[math]\displaystyle{
G_0 =
\left[ \begin{array} {r}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
\quad
𝒈_0 =
\left[ \begin{array} {r}
1200.000 & 696.578 \\
\end{array} \right]
\\[20pt]
G_1 =
\left[ \begin{array} {r}
\frac73 & \frac13 \\
-\frac43 & -\frac13 \\
\frac13 & \frac13 \\
\end{array} \right]
\quad
𝒈_1 =
\left[ \begin{array} {r}
1192.831 & 694.786 \\
\end{array} \right]
}[/math]
So [math]\displaystyle{ 𝜹_1 = 𝒈_1 - 𝒈_0 }[/math] = {-7.169 -1.792]. Suppose we get [math]\displaystyle{ 𝒃 }[/math] = [0.5]. We know that [math]\displaystyle{ 𝒃D }[/math] = {-3.584 -0.896]. So [math]\displaystyle{ 𝒈 }[/math] should be [math]\displaystyle{ 𝒈_0 + 𝒃D }[/math] = {1200 696.578] + {-3.584 -0.896] = {1196.416 695.682].
But do we find the same tuning with [math]\displaystyle{ G = G_0 + b_1(G_1 - G_0) + b_2(G_2 - G_0) + \ldots + b_{τ-1}(G_{τ-1} - G_0) }[/math]? That's the key question. (In this case, we have to bust the matrix multiplication up. That is, there's no way to replace the rows of D with entire matrices. Cumbersome, but reality.)
In this case we only have the one delta, [math]\displaystyle{ G_1 - G_0 = }[/math]
[math]\displaystyle{
\left[ \begin{array} {r}
\frac73 & \frac13 \\
-\frac43 & -\frac13 \\
\frac13 & \frac13 \\
\end{array} \right]
-
\left[ \begin{array} {r}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
=
\left[ \begin{array} {r}
\frac43 & \frac13 \\
-\frac43 & -\frac13 \\
\frac13 & \frac{1}{12} \\
\end{array} \right]
}[/math]
And so [math]\displaystyle{ b_1(G_1 - G_0) }[/math], or half of that, is:
[math]\displaystyle{
\left[ \begin{array} {r}
\frac23 & \frac16 \\
-\frac23 & -\frac16 \\
\frac16 & \frac{1}{24} \\
\end{array} \right]
}[/math]
And add that to [math]\displaystyle{ G_0 }[/math] then:
[math]\displaystyle{
\left[ \begin{array} {r}
1 & 0 \\
0 & 0 \\
0 & \frac14 \\
\end{array} \right]
+
\left[ \begin{array} {r}
\frac23 & \frac16 \\
-\frac23 & -\frac16 \\
\frac16 & \frac{1}{24} \\
\end{array} \right]
=
\left[ \begin{array} {r}
\frac53 & \frac16 \\
-\frac23 & -\frac16 \\
\frac16 & \frac{9}{24} \\
\end{array} \right]
}[/math]
So [math]\displaystyle{ \textbf{g}_1 }[/math] here, the first column, [[math]\displaystyle{ \frac53 }[/math] [math]\displaystyle{ -\frac23 }[/math] [math]\displaystyle{ \frac16 }[/math]⟩, is [math]\displaystyle{ 2^{\frac53}3^{-\frac23}5^{\frac16} \approx 1.996 }[/math]. So [math]\displaystyle{ g_1 }[/math] = 1196.416 ¢.
And [math]\displaystyle{ \textbf{g}_2 }[/math] here, the second column, {{vector|[math]\displaystyle{ \frac16 }[/math] [math]\displaystyle{ -\frac16 }[/math] [math]\displaystyle{ \frac{9}{24} }[/math]⟩, is [math]\displaystyle{ 2^{\frac16}3^{-\frac16}5^{\frac{9}{24}} \approx 1.495 }[/math]. So [math]\displaystyle{ g_2 }[/math] = 695.682 ¢.
Perfect! We wanted {1196.416 695.682] and we got it.
Now maybe this doesn't fully test the system, since we only convexly combined two tunings, but this is probably sound for general use. At least, the test suite of the RTT Library in Wolfram Language included several examples that should have failed upon switching to this way of computing true optimum tunings if this were a problem, but they did not.
Polytope
Keenan Pepper named the file where we wrote the coinciding-damage method "tiptop.py", and along with that coined the tuning scheme name "TIP-TOP", for "Tiebreaker-in-polytope TOP".[note 23] So what's up with this "polytope"?
Polytopes — they're nothing too scary, actually. The name seems imposing, but it's really just a name for a shape which is as generic as possible:
- The "poly-" part means generic to how many vertices/edges/faces/etc. the shape has. This prefix generalizes prefixes you may be familiar with like "tetra-", "penta-", "hexa-", etc., which are used for shapes where we do know exactly how many of the given type of feature a shape has, like a "penta-gon" (5 edges) or a "tetra-hedron" (4 faces).
- The "-tope" part means generic to how many dimensions these features occupy. This suffix generalizes suffixes you may be familiar with like "-gon", "-hedron", "-choron"/"-cell"/"-hedroid", etc., which are used for shapes where we do know exactly how many dimensions a shape occupies, again, like a "hexa-gon" (2 dimensions) or an "octa-hedron" (3 dimensions).
We note that the polytope Keenan refers to is not the full coinciding-damage point set.
It's not even the faceted bowl we see formed from the aerial view by the combination of all the individual target-intervals' tuning damage graph hyper-V's; that's an in-between sized point set we would call the "maximum damage graph vertices".
No, Keenan's polytope refers to an even smaller set of points. It contains either only a single point for the case of an immediately unique optimum, or more than one point which together bound the region (such as a line segment, triangle, etc.) within which the true optimum may be found in the next iteration of the algorithm, using blends. This is what we could call the minimax polytope.
Major modification to Keenan's original method
In the beginning of our discussion of the coinciding-damage method, we mentioned that Douglas Blumeyer had modified Keenan Pepper's algorithm in a way that "simplifies it conceptually and allows it to identify optimum tunings more quickly". Here is an explanation of that change.
Keenan's original design was to only include the zero-damage points once tuning damage space had been reduced to 2D. This design still does eventually finds the same true optimum tunings, but the problem is that it requires advanced tie-breaking to accomplish this, where basic tie-breaking could have worked had those points been included. Consider the case of {2/1,3/1,5/1,6/5} minimax-U blackwood we gave as our basic tie-breaking example here: with Keenan's design, the intersection between [math]\displaystyle{ \frac51 }[/math] and [math]\displaystyle{ \frac65 }[/math]'s creases would not have been included; it would have been as if we were doing the primes minimax-U blackwood example we look at in the following section where basic tie-breaking must fail.
Since advanced tie-breaking requires an entire new iteration of the algorithm, gathering a whole new coinciding-damage point set, it is more computationally expensive than handling a tie-break with the basic technique by simply including some more points in the current iteration.
Also, because always including zero-damage points is a conceptually purer way of presenting the concepts (it doesn't require an entire 7-page separate section to this article explaining the single-free-generator 2D tuning damage space exception, which as you might guess, I did write before having the necessary insight to simplify things), it is preferable for human understanding as well.
I also considered adding the unison to the target-interval set in order to capture the zero-damage points, but that was terribly inefficient and confusing. I also tried generalizing Keenan's code in a different way. Keenan's code includes [math]\displaystyle{ K }[/math] which make a target-interval itself unchanged, but it only does that when the [math]\displaystyle{ K }[/math] have only one column (meaning we're searching 2D tuning damage space). What if we think of it like this: our point set always includes [math]\displaystyle{ K }[/math] which have one column for enforcing a target-interval itself, among any other unchanged-intervals, and we do this not only when [math]\displaystyle{ K }[/math] is one column. That turned out to be an improvement, but it still resulted in redundant points, because we don't need direction permutations for the non-unison target-intervals when their errors are 0 either (e.g. If [math]\displaystyle{ \frac21 }[/math] is pure, and [math]\displaystyle{ \frac61 }[/math] is pure, that implies that [math]\displaystyle{ \frac31 }[/math] is pure. But if [math]\displaystyle{ \frac21 }[/math] is pure, and [math]\displaystyle{ \frac32 }[/math] is pure, that just as well implies that [math]\displaystyle{ \frac31 }[/math] is pure.
Why we abbreviate
For some readers, it may seem pointless, or wasteful, to abbreviate DSLODs like this. Especially in those cases where you're tantalizingly close… you can see that you could break a tie, if only you were allowed to include one more entry in each ADSLOD. Or perhaps you could at least reduce the count of tunings that are tied.
Well, here's another way to think about the reason for this abbreviation, which may help you respect the purpose for the abbreviation. If you falsely eliminate tunings that rightly should still have been tied at this stage, then you will be eliminating tunings that should have been helping to define the boundary of the region to check in the next iteration of the method.
So, if you erroneously reduced the search space down to two tuning points defining a line segment region, you should have been searching an entire triangle-shaped region instead. You might miss the true optimum somewhere in the middle of the area of that triangle, not merely along one of its three sides.
Importance of deduplication
Note that a very good reason to perform the type of deduplication within the target-interval set discussed earlier in this article (here) is to prevent unnecessary failing of the basic tie-breaking mechanism. Suppose we have a case like our basic tie-breakable blackwood example, where two damage graphs' crease is parallel to the floor and forms the minimum of the max damage graph, but we can still look one more position down the ADSLODs to tie-break at some point in the middle of this line segment range which minimizes the third damage position. Well, now imagine that instead we clogged our ADSLODs with a duplicate target-interval, i.e. one whose damage graph is identical to one or the other of these two forming this tied minimax crease. Now we unnecessarily find ourselves with three coinciding damages up top instead of just two, and will be forced to dip into advanced tie-breaking. But if we had only de-duped the target-intervals which map to the same mapped interval up front, we wouldn't have had to do that.
Held-intervals with respect to advanced tie-breaking
In this section we discuss how to handle held-intervals with the coinciding-damage method. We note here that the extra steps involved—allocating columns of the constraint matrices to the held-intervals—are only necessary in the first iteration of the method.
Think of it this way: whichever generators were locked into the appropriate proportion in order to achieve the held-intervals at the top-level, main tuning damage space, those will remain locked in the blends of tunings at lower levels. In other words, whatever cross-section we take to capture the minimax polytope will already be within the held-interval subregion of tuning damage space.
A major flaw with the method
Keenan himself considers his algorithm to be pretty dumb. (It seems sort of fantastically powerful and genius to me, overall, but I can sort of see what he means a bit, now).
One core problem it has causes it to be potentially majorly inefficient, and also somewhat conceptually misleading. That's what we'll discuss here.
When we introduced the concept of blends in an earlier section, we noted how any point within the bounded region can be specified as a blend where the blending variables are positive sum to 1. That's the key thing that keeps us within the region; if we can specify huge and/or negative blending variables, then the exercise is moot, and we can specify points anywhere. Well, if we've got some 1D line segment embedded in a 2D plane, without the sum-to-1 rule, we can use [math]\displaystyle{ \mathbf{A} }[/math] and [math]\displaystyle{ \mathbf{B} }[/math] to describe any point within that 2D plane, anyway.
So, it turns out that this is essentially the same as how it works in advanced tie-breaking. When we take a cross-section of tuning damage space which contains the line segment of our tied basic minimax region, and gather a new coinciding-damage point set in terms of blending variables, we don't know if a point is going to fall within the line segment we care about or not until after we've already computed its blend variables. (Remember, the blend variable for the anchor tuning is always assumed to be whatever is required to get the sum exactly to 1, so all we care about is the other variables summing to something between 0 and 1.)
For example, consider the diagram we showed in this section. Note how the damage graphs for [math]\displaystyle{ \frac52 }[/math] and [math]\displaystyle{ \frac{16}{5} }[/math] intersect (within this cross-section) but just outside the range where [math]\displaystyle{ 0 \lt b_1 \lt 1 }[/math]. Well, when we gather our coinciding-damage points, convert their ReDPOTICs and STICs to constraint matrices, and convert those to tunings, it's not until then that we'll realize this tuning is outside of bounds. We could filter it out at this point—it will never qualify as the true optimum tuning, because if you look straight up in the diagram, you can see that the damage to [math]\displaystyle{ \frac95 }[/math] is greater than the basic minimax could potentially be. But we already wasted a lot of resources finding it.
Essentially we search the whole cross-section, not just the minimax polytope we've identified.
And there's no particularly obvious way to rework this method to only find coinciding-damage points for [math]\displaystyle{ K }[/math] where every entry of [math]\displaystyle{ 𝒃 }[/math] is non-negative and [math]\displaystyle{ \llzigzag 𝒃 \rrzigzag_1 = 1 }[/math]. To improve this part of the algorithm would require basically rethinking it from the inside out.
Derivation of extracted anchor
We can derive this formula from the one we had before, like so. Start with:
[math]\displaystyle{
\mathbf{P} = x\mathbf{A} + y\mathbf{B} + z\mathbf{C}
}[/math]
Add [math]\displaystyle{ \mathbf{A} - \mathbf{A} }[/math] to this, which changes nothing.
[math]\displaystyle{
\mathbf{P} = \mathbf{A} - \mathbf{A} + x\mathbf{A} + y\mathbf{B} + z\mathbf{C}
}[/math]
Recognize a coefficient of [math]\displaystyle{ 1 }[/math] on the subtracted [math]\displaystyle{ \mathbf{A} }[/math].
[math]\displaystyle{
\mathbf{P} = \mathbf{A} - 1\mathbf{A} + x\mathbf{A} + y\mathbf{B} + z\mathbf{C}
}[/math]
We know [math]\displaystyle{ x + y + z = 1 }[/math], so we can substitute that in for this [math]\displaystyle{ 1 }[/math].
[math]\displaystyle{
\mathbf{P} = \mathbf{A} - (x + y + z)\mathbf{A} + x\mathbf{A} + y\mathbf{B} + z\mathbf{C}
}[/math]
Distribute.
[math]\displaystyle{
\mathbf{P} = \mathbf{A} - x\mathbf{A} - y\mathbf{A} - z\mathbf{A} + x\mathbf{A} + y\mathbf{B} + z\mathbf{C}
}[/math]
Regroup by [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math].
[math]\displaystyle{
\mathbf{P} = \mathbf{A} + x(\mathbf{A} - \mathbf{A}) + y(\mathbf{B} - \mathbf{A}) + z(\mathbf{C} - \mathbf{A})
}[/math]
Cancel out these [math]\displaystyle{ \mathbf{A} }[/math]'s and thus [math]\displaystyle{ x }[/math].
[math]\displaystyle{
\mathbf{P} = \mathbf{A} + x(\cancel{\mathbf{A}} - \cancel{\mathbf{A}}) + y(\mathbf{B} - \mathbf{A}) + z(\mathbf{C} - \mathbf{A})
\mathbf{P} = \mathbf{A} + x(0) + y(\mathbf{B} - \mathbf{A}) + z(\mathbf{C} - \mathbf{A})
}[/math]
And so our final formula:
[math]\displaystyle{
\mathbf{P} = \mathbf{A} + y(\mathbf{B} - \mathbf{A}) + z(\mathbf{C} - \mathbf{A})
}[/math]
Equivalence to power-limit approach
In Keenan's original Yahoo groups post, he claims that his method (the core idea of which is explained in a modified form here as the coinciding-damage method) is equivalent to the power-limit method for finding true optimums for minimax tunings: "This is equivalent to taking the limit of the Lp norm minimizer as p tends to infinity (exercise for the reader!)"[note 24]. Douglas Blumeyer has attempted this exercise, but failed. He pestered Keenan himself for the solution, but it had been so long (about 10 years) since Keenan wrote this, he himself could not reproduce. So at this time, this remains an open problem—an exercise for you readers, now.
Normalization required to handle exact tunings
One complication arose with the advanced tie-breaking part of the code (in Dave Keenan & Douglas Blumeyer's RTT Library in Wolfram Language which was adapted from Keenan Pepper's original Python code) upon the switch from Keenan's original technique of computing approximate generator tuning maps [math]\displaystyle{ 𝒈 }[/math] by solving linear systems of equations to Dave Keenan's technique of computing exact generator embeddings [math]\displaystyle{ G }[/math] by doing matrix inverses. In some cases where Keenan's technique used to work fine, Dave's method would fall on its face. Here's what happened.
Essentially, the basic tie-breaking step would come back with a set of tied tunings such as this:
- [math]\displaystyle{ 𝒈_0 }[/math] = {240.000 2786.314]
- [math]\displaystyle{ 𝒈_1 }[/math] = {240.000 2795.336]
- [math]\displaystyle{ 𝒈_2 }[/math] = {240.000 2804.359]
The problem is that when we have three points defining a convex hull, it's supposed to be a triangle! This is a degenerate case where all three points fall along the same line. Not only is this wasteful, but it also screws stuff up, because now there's essentially more than one way to blend [math]\displaystyle{ \mathbf{A} }[/math], [math]\displaystyle{ \mathbf{B} }[/math], and [math]\displaystyle{ \mathbf{C} }[/math] together to get [math]\displaystyle{ \mathbf{P} }[/math], because [math]\displaystyle{ \mathbf{B} }[/math] and [math]\displaystyle{ \mathbf{C} }[/math] pull us away from [math]\displaystyle{ \mathbf{A} }[/math] in the exact same direction.
Note that the only thing that matters is the direction that the tied tunings are from each other, not the distance; the values in the blend map [math]\displaystyle{ 𝒃 }[/math] are continuous and can be anything they need to be to reach a desired point. In other words, all that matters are the proportions of the entries of the deltas to each other. In still other words, different tunings on the same line are redundant.
It happens to be the case here that the [math]\displaystyle{ 𝜹_i }[/math] are not only on the same line, but simple multiples of each other:
- [math]\displaystyle{ 𝜹_2 = 𝒈_1 - 𝒈_0 }[/math] = {240.000 2795.336] - {240.000 2786.314] = {0 9.0225]
- [math]\displaystyle{ 𝜹_1 = 𝒈_2 - 𝒈_0 }[/math] = {240.000 2804.359] - {240.000 2786.314] = {0 18.045]
which is to say that [math]\displaystyle{ 𝒈_1 }[/math] happens to be smack-dab halfway between [math]\displaystyle{ 𝒈_0 }[/math] and [math]\displaystyle{ 𝒈_1 }[/math]. But that's just a distraction; that's not important. It could have been [math]\displaystyle{ ϕ }[/math] of the way between them instead and the problem would have been the same.
Remember that these [math]\displaystyle{ 𝜹_i }[/math] get combined into one big [math]\displaystyle{ D }[/math] matrix. In this case, that's
[math]\displaystyle{
\left[ \begin{array} {r}
0 & 9.0225 \\
0 & 18.045 \\
\end{array} \right]
}[/math]
Using this for [math]\displaystyle{ D }[/math], however, causes every [math]\displaystyle{ B }[/math] we try to find via
[math]\displaystyle{
B = \mathrm{T}WK(DM\mathrm{T}WK)^{-1}
}[/math]
to fail, because the [math]\displaystyle{ DM\mathrm{T}WK }[/math] matrix we try to invert is singular. (And for one reason or another, Keenan's way, using a LinearSolve[], handled this degenerate case without complaining.)
One might think the solution would be simply to canonicalize this [math]\displaystyle{ D }[/math] matrix: HNF it, and delete the all-zero rows. But here's the thing: it's not an integer matrix. It's not even rational. Even though it's seems obvious that since [math]\displaystyle{ 18.045 = 9.0225 × 2 }[/math] we should be able to reduce this thing to:
[math]\displaystyle{
\left[ \begin{array} {r}
0 & 1 \\
0 & 2 \\
\end{array} \right]
}[/math]
actually what we want to do here is different and maybe slightly simpler. At least, it's a different breed of normalization.
What the RTT Library in Wolfram Language does now is Normalize[] every [math]\displaystyle{ 𝜹_i }[/math] to a unit vector and then dedupe them according to if they equal each other or their negation. Given the design of the algorithm, namely, how it doesn't actually restrict itself to searching the convex combination but instead searches the whole affine plane or whatever. And that works.
As a result, however, it doesn't always work directly in blend variables, but in scaled blend variables, scaled by the factor between the normalized and non-normalized deltas. For example, normalizing the above example would create a normalizing size factor of 9.0225. So now the tied minimax range wouldn't be from [math]\displaystyle{ 0 \lt b_1 \lt 1 }[/math], but from [math]\displaystyle{ 0 \lt b_1 \lt 9.0225 }[/math].
For all-interval tuning schemes
When computing an all-interval tuning where the dual norm power is [math]\displaystyle{ ∞ }[/math], we use a variation on the method we used for ordinary tunings when the optimization power was [math]\displaystyle{ ∞ }[/math].
In this case, our optimization power is also still [math]\displaystyle{ ∞ }[/math]. That is to say, that in this case we're doing the same computation we would have been doing if we had a finite target-interval set, but now we're doing it as if the primes alone were our target-interval set.
Let's get the minimax-S tuning of meantone. With three proxy target-intervals and two generators, we end up with four constraint matrices:
[math]\displaystyle{
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
,
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & {-1} \\
\end{array} \right]
,
\left[ \begin{array} {rrr}
+1 & +1 \\
{-1} & 0 \\
0 & +1 \\
\end{array} \right]
,
\left[ \begin{array} {rrr}
+1 & +1 \\
{-1} & 0 \\
0 & {-1} \\
\end{array} \right]
}[/math]
These correspond to tunings with the following pairs (one for each generator) of unchanged-intervals:
- [math]\displaystyle{ (\frac21)^1 × (\frac31)^1 = \frac61 }[/math] and [math]\displaystyle{ (\frac21)^1 × (\frac51)^1 = \frac{10}{1} }[/math]
- [math]\displaystyle{ (\frac21)^1 × (\frac31)^1 = \frac61 }[/math] and [math]\displaystyle{ (\frac21)^1 × (\frac51)^{-1} = \frac{2}{5} }[/math]
- [math]\displaystyle{ (\frac21)^1 × (\frac31)^{-1} = \frac23 }[/math] and [math]\displaystyle{ (\frac21)^1 × (\frac51)^1 = \frac{10}{1} }[/math]
- [math]\displaystyle{ (\frac21)^1 × (\frac31)^{-1} = \frac23 }[/math] and [math]\displaystyle{ (\frac21)^1 × (\frac51)^{-1} = \frac{2}{5} }[/math]
Which in turn become the following tunings:
- ⟨1202.682 695.021]
- ⟨1201.699 697.564]
- ⟨1195.387 699.256]
- ⟨0.000 0.000] (Yup, not kidding. This tuning is probably not going to win…)
And these in turn give the following prime absolute error lists (for each list, all three primes have coinciding absolute scaled errors, because minimax tunings lead to [math]\displaystyle{ r + 1 }[/math] of them coinciding):
- ⟨2.682 2.682 2.682]
- ⟨1.699 1.699 1.699]
- ⟨4.613 4.613 4.613]
- ⟨1200.000 1200.000 1200.000]
And so our second tuning wins, and that's our minimax-S tuning of meantone.
With alternative complexities
The following examples all pick up from a shared setup here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Computing all-interval tuning schemes with alternative complexities.
So for all complexities used here—at least the first several simpler examples—our constraint matrices will be:
[math]\displaystyle{
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
, \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & -1 \\
\end{array} \right]
, \\
\left[ \begin{array} {rrr}
+1 & +1 \\
-1 & 0 \\
0 & +1 \\
\end{array} \right]
, \\
\left[ \begin{array} {rrr}
+1 & +1 \\
-1 & 0 \\
0 & -1 \\
\end{array} \right]
}[/math]
Minimax-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Log-product2, by plugging [math]\displaystyle{ L^{-1} }[/math] into our pseudoinverse method for [math]\displaystyle{ S_{\text{p}} }[/math].
[math]\displaystyle{ % \slant{} command approximates italics to allow slanted bold characters, including digits, in MathJax. \def\slant#1{\style{display:inline-block;margin:-.05em;transform:skew(-14deg)translateX(.03em)}{#1}} }[/math] Now we need to find the tunings corresponding to our series of constraint matrices [math]\displaystyle{ K }[/math]. Those constraint matrices apply to both sides of the approximation [math]\displaystyle{ GM\mathrm{T}_{\text{p}}S_{\text{p}} \approx \mathrm{T}_{\text{p}}S_{\text{p}} }[/math], or simplified, [math]\displaystyle{ GMS_{\text{p}} \approx S_{\text{p}} }[/math]. So first we find [math]\displaystyle{ MS_{\text{p}} = ML^{-1} = }[/math] [⟨[math]\displaystyle{ \frac{1}{\log_2(2)} }[/math] [math]\displaystyle{ \frac{2}{\log_2(3)} }[/math] [math]\displaystyle{ \frac{3}{\log_2(5)} }[/math]] ⟨[math]\displaystyle{ \frac{0}{\log_2(2)} }[/math] [math]\displaystyle{ \frac{-3}{\log_2(3)} }[/math] [math]\displaystyle{ \frac{-5}{\log_2(5)} }[/math]]}. And then we find [math]\displaystyle{ S_{\text{p}} = L^{-1} = \text{diag}(\left[ \begin{array} {r} \frac{1}{\log_2(2)} & \frac{1}{\log_2(3)} & \frac{1}{\log_2(5)} \end{array} \right]) }[/math].
So here's our first constraint matrix:
[math]\displaystyle{
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
}[/math]
Applying the constraint to get an equality:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
\begin{array} {c}
ML^{-1} \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} \\
\frac{0}{\log_2(2)} & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
L^{-1} \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & 0 & 0 \\
0 & \frac{1}{\log_2(3)} & 0 \\
0 & 0 & \frac{1}{\log_2(5)} \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
}[/math]
Multiply:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
\begin{array} {c}
ML^{-1}K \\
\left[ \begin{array} {rrr}
1+\frac{2}{\log_2(3)} & 1+\frac{3}{\log_2(5)} \\
\frac{-3}{\log_2(3)} & \frac{5}{\log_2(5)} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
L^{-1}K \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & \frac{1}{\log_2(2)} \\
\frac{1}{\log_2(3)} & 0 \\
0 & \frac{1}{\log_2(5)}\\
\end{array} \right]
\end{array}
}[/math]
Solve for [math]\displaystyle{ G }[/math]:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
L^{-1}K \\
\left[ \begin{array} {rrr}
\frac{1}{\log_2(2)} & \frac{1}{\log_2(2)} \\
\frac{1}{\log_2(3)} & 0 \\
0 & \frac{1}{\log_2(5)}\\
\end{array} \right]
\end{array}
\begin{array} {c}
(ML^{-1}K)^{-1} \\
\left[ \begin{array} {rrr}
\frac{-5}{\log_2(5)} & {-1}-\frac{3}{\log_2(5)} \\
\frac{3}{\log_2(3)} & 1+\frac{2}{\log_2(3)} \\
\end{array} \right] \\
\hline
(\frac{3}{\log_2(3)} - \frac{5}{\log_2(5)} - \frac{1}{\log_2(3)\log_2(5)})
\end{array}
=
\begin{array} {c}
\\
\left[ \begin{array} {rrr}
0.490 & 0.0567 \\
2.552 & 2.717 \\
-1.531 & -1.830 \\
\end{array} \right]
\end{array}
}[/math]
From that we can find [math]\displaystyle{ 𝒈 = 𝒋G }[/math] to get [math]\displaystyle{ g_1 = 1174.903 }[/math] and [math]\displaystyle{ g_2 = 136.024 }[/math].
Sure, that looks like a horrible tuning; it only minimizes the maximum damage across all intervals to about 25 ¢(S)! But don't worry yet. This is all part of the process. We've only checked our first of four constraint matrices. Certainly one of the other three will lead to a better candidate tuning. We won't work through these examples in detail; one illustrative example should be enough.
Indeed we find that the second one to be [math]\displaystyle{ 𝒈 = }[/math] {1196.906 162.318] dealing only 3 ¢(S) maximum damage. And the third [math]\displaystyle{ K }[/math] leads to {1203.540 166.505] which also deals just over 3 ¢(S) maximum damage. The fourth [math]\displaystyle{ K }[/math] is a dud, sending the tuning to {0 0], dealing a whopping 1200 ¢(S) maximum damage.
And so the minimax-S tuning of this temperament is {1196.906 162.318]. We could compute this in the RTT Library in Wolfram Language with the following line of code:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "minimax-S"]
Out: {1196.906 162.318]
Minimax-sofpr-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Sum-of-prime-factors-with-repetition2. Plugging [math]\displaystyle{ \text{diag}(𝒑)^{-1} }[/math] in for [math]\displaystyle{ S_{\text{p}} }[/math].
Now we need to find the tunings corresponding to our series of constraint matrices [math]\displaystyle{ K }[/math]. Those constraint matrices apply to both sides of the approximation [math]\displaystyle{ GM\mathrm{T}_{\text{p}}S_{\text{p}} \approx \mathrm{T}_{\text{p}}S_{\text{p}} }[/math], or simplified, [math]\displaystyle{ GMS_{\text{p}} \approx S_{\text{p}} }[/math]. So first we find [math]\displaystyle{ MS_{\text{p}} = M\text{diag}(𝒑)^{-1} = }[/math] [⟨[math]\displaystyle{ \frac{1}{2} }[/math] [math]\displaystyle{ \frac{2}{3} }[/math] [math]\displaystyle{ \frac{3}{5} }[/math]] ⟨[math]\displaystyle{ \frac{0}{2} }[/math] [math]\displaystyle{ \frac{-3}{3} }[/math] [math]\displaystyle{ \frac{-5}{5} }[/math]]}. And then we find [math]\displaystyle{ S_{\text{p}} = \text{diag}(𝒑)^{-1} = \text{diag}(\left[ \begin{array} {r} \frac12 & \frac13 & \frac15 \end{array} \right]) }[/math].
So here's our first constraint matrix:
[math]\displaystyle{
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
}[/math]
Applying the constraint to get an equality:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
\begin{array} {c}
M\text{diag}(𝒑)^{-1} \\
\left[ \begin{array} {rrr}
\frac12 & \frac23 & \frac35 \\
\frac02 & \frac{-3}{3} & \frac{-5}{5} \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{diag}(𝒑)^{-1} \\
\left[ \begin{array} {rrr}
\frac12 & 0 & 0 \\
0 & \frac13 & 0 \\
0 & 0 & \frac15 \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
}[/math]
Multiply:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
\begin{array} {c}
M\text{diag}(𝒑)^{-1}K \\
\left[ \begin{array} {rrr}
\frac76 & \frac{11}{10} \\
{-1} & {-1} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{diag}(𝒑)^{-1}K \\
\left[ \begin{array} {rrr}
\frac12 & \frac12 \\
\frac13 & 0 \\
0 & \frac15 \\
\end{array} \right]
\end{array}
}[/math]
Solve for [math]\displaystyle{ G }[/math]:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{diag}(𝒑)^{-1}K \\
\left[ \begin{array} {rrr}
\frac12 & \frac12 \\
\frac13 & 0 \\
0 & \frac15 \\
\end{array} \right]
\end{array}
\begin{array} {c}
(M\text{diag}(𝒑)^{-1}K)^{-1} \\
\left[ \begin{array} {rrr}
15 & \frac{33}{2} \\
{-15} & {-\frac{35}{2}} \\
\end{array} \right] \\
\end{array}
=
\begin{array} {c}
\\
\left[ \begin{array} {rrr}
0 & {-\frac{1}{2}} \\
5 & \frac{11}{2} \\
-3 & {-\frac{7}{2}} \\
\end{array} \right]
\end{array}
}[/math]
Note the tempered octave is exactly [math]\displaystyle{ 3^{5}5^{-3} = \frac{243}{125} }[/math]! That sounds cool, but it's actually an entire quartertone narrow. We find [math]\displaystyle{ g_1 = 1150.834 }[/math] and [math]\displaystyle{ g_2 = 108.655 }[/math]. Again, that looks like a horrible tuning; this first constraint matrix is beginning to seem so hot for tuning porcupine temperament, irrespective of our choice of complexity.
But again that the second candidate tuning to be much nicer, with [math]\displaystyle{ 𝒈 = }[/math] {1196.927 162.430] dealing only about 1.5 ¢(S) maximum damage. And the third [math]\displaystyle{ K }[/math] leads to {1203.512 166.600] which also deals about 1.8 ¢(S) maximum damage. The fourth [math]\displaystyle{ K }[/math] is a dud, giving {1150.834 157.821], dealing a whopping 25 ¢(S) maximum damage.
And so the minimax-sopfr-S tuning of this temperament is {1196.927 162.430]. We could compute this in the RTT Library in Wolfram Language with the following line of code:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "minimax-sopfr-S"]
Out: {1196.927 162.430]
Minimax-copfr-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Count-of-prime-factors-with-repetition2. Plugging [math]\displaystyle{ I }[/math] into our pseudoinverse method for [math]\displaystyle{ S_{\text{p}} }[/math].
Now we need to find the tunings corresponding to our series of constraint matrices [math]\displaystyle{ K }[/math]. Those constraint matrices apply to both sides of the approximation [math]\displaystyle{ GM\mathrm{T}_{\text{p}}S_{\text{p}} \approx \mathrm{T}_{\text{p}}S_{\text{p}} }[/math], or simplified, [math]\displaystyle{ GMS_{\text{p}} \approx S_{\text{p}} }[/math]. So first we find [math]\displaystyle{ MS_{\text{p}} = M = }[/math] [⟨1 2 3] ⟨0 -3 -5]}. And then we find [math]\displaystyle{ S_{\text{p}} = I }[/math].
So here's our first constraint matrix:
[math]\displaystyle{
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
}[/math]
Applying the constraint to get an equality:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
\begin{array} {c}
M \\
\left[ \begin{array} {rrr}
1 & 2 & 3 \\
0 & {-3} & {-5} \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
I \\
\left[ \begin{array} {rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
+1 & +1 \\
+1 & 0 \\
0 & +1 \\
\end{array} \right]
\end{array}
}[/math]
Multiply:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
\begin{array} {c}
MK \\
\left[ \begin{array} {rrr}
3 & 4 \\
{-3} & {-5} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
IK \\
\left[ \begin{array} {rrr}
1 & 1 \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
}[/math]
Solve for [math]\displaystyle{ G }[/math]:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rrr}
g_{11} & g_{12} \\
g_{21} & g_{22} \\
g_{31} & g_{32} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
K \\
\left[ \begin{array} {rrr}
1 & 1 \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
\end{array}
\begin{array} {c}
(MK)^{-1} \\
\left[ \begin{array} {rrr}
\frac53 & \frac43 \\
{-1} & {-1} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\\
\dfrac13
\left[ \begin{array} {rrr}
2 & 1 \\
5 & 4 \\
{-3} & {-3} \\
\end{array} \right]
\end{array}
}[/math]
So that's a tempered octave equal to [math]\displaystyle{ 2^{\frac23}3^{\frac53}5^{-\frac33} = \sqrt[3]{\frac{972}{125}} }[/math]. Interesting, perhaps. But we find [math]\displaystyle{ g_1 = 1183.611 }[/math] and [math]\displaystyle{ g_2 = 149.626 }[/math]. You know the drill by now. This one's a horrible tuning. It does 16 ¢(S) damage.
The second constraint gives [math]\displaystyle{ 𝒈 = }[/math] {1194.537 160.552] dealing only 5 ¢(S) maximum damage. And the third [math]\displaystyle{ K }[/math] leads to {1207.024 168.356] which also deals just over 7 ¢(S) maximum damage. The fourth [math]\displaystyle{ K }[/math] is a dud, sending the tuning to {1249.166 182.404], dealing nearly 50 ¢(S) maximum damage.
And so the minimax-copfr-S tuning of this temperament is {1194.537 160.552]. We could compute this in the RTT Library in Wolfram Language with the following line of code:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "minimax-copfr-S"]
Out: {1194.537 160.552]
In the case of minimax-copfr-S with nullity-1 (only one comma) like this, we actually have a shortcut. First, take the size of the comma in cents, and divide it by its total count of primes. The porcupine comma is [math]\displaystyle{ \frac{250}{243} }[/math], or in vector form [1 -5 3⟩, and so it has |1| + |-5| + |3| = 9 total primes. And being 49.166 ¢ in size, that gives us [math]\displaystyle{ \frac{49.166}{9} = 5.463 }[/math]. What's this number for? That's the amount of cents to retune each prime by! If the count of a prime in the comma is positive, we tune narrow by that much, and if negative, we tune wide. So the map for the minimax-copfr-S tuning of porcupine is [math]\displaystyle{ 𝒕 }[/math] = ⟨1200 1901.955 2786.314] + ⟨-5.463 5.463 -5.463] = ⟨1194.537 1907.418 2780.851]. If you're not convinced this matches the [math]\displaystyle{ 𝒈 }[/math] we found the long way, feel free to check via [math]\displaystyle{ 𝒕 = 𝒈M }[/math].
Minimax-lils-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Log-integer-limit-squared2.
Now we need to find the tunings corresponding to our series of constraint matrices [math]\displaystyle{ K }[/math]. Those constraint matrices apply to both sides of the approximation [math]\displaystyle{ GM\mathrm{T}_{\text{p}}S_{\text{p}} \approx \mathrm{T}_{\text{p}}S_{\text{p}} }[/math], or simplified, [math]\displaystyle{ GMS_{\text{p}} \approx S_{\text{p}} }[/math], or equivalent thereof. So first we find [math]\displaystyle{ M\mathrm{T}_{\text{p}}S_{\text{p}} }[/math]. According to Mike's augmentation pattern[note 25], we get:
[math]\displaystyle{
\left[ \begin{array} {rrr|r}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
}[/math]
(Compare with the result for minimax-S, the same but without the augmentations.)
And then we find [math]\displaystyle{ S_{\text{p}} }[/math] or equivalent thereof. It's an augmentation of [math]\displaystyle{ L^{-1} }[/math]:
[math]\displaystyle{
\left[ \begin{array} {rrr|r}
\frac{1}{\log_2(2)} & 0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
}[/math]
This is an extrapolation from Mike's augmentation pattern. It's not actually directly any sort of inverse of the complexity pretransformer. In some sense, that effect has already been built into the augmentation of [math]\displaystyle{ M\mathrm{T}_{\text{p}}S_{\text{p}} }[/math]. (Again, it's the same as minimax-S, but with the augmentation.)
On account of the augmentation, our constraint matrices are a bit different here. Actually, we have twice as many candidate tunings to check this time (if you compare this list with the one given in the opening part of this supersection, the pattern relating them is fairly clear). The extra dimension is treated just like it would be otherwise. Here are all of our [math]\displaystyle{ K }[/math]'s:
[math]\displaystyle{
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & +1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{+1} \\
\end{array} \right]
, \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & +1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
, \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & -1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{+1} \\
\end{array} \right]
, \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & -1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
, \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
-1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & +1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{+1} \\
\end{array} \right]
, \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
-1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & +1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
, \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
-1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & -1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{+1} \\
\end{array} \right]
, \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
-1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & -1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{-1} \\
\end{array} \right]
, \\
}[/math]
So let's just work through one tuning with the first [math]\displaystyle{ K }[/math]. Note that we've also augmented [math]\displaystyle{ G }[/math]. This augmentation is necessary for the computation but will be thrown away once we have our result.
Applying the constraint to get an equality:
[math]\displaystyle{
\scriptsize
\begin{array} {c}
G \\
\left[ \begin{array} {rr|r}
g_{1,1} & g_{1,2} & \style{background-color:#FFF200;padding:5px}{g_{1,\text{aug}}} \\
g_{2,1} & g_{2,2} & \style{background-color:#FFF200;padding:5px}{g_{2,\text{aug}}} \\
g_{3,1} & g_{3,2} & \style{background-color:#FFF200;padding:5px}{g_{3,\text{aug}}} \\
\hline
\style{background-color:#FFF200;padding:5px}{g_{\text{aug},1}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},2}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},\text{aug}}} \\
\end{array} \right]
\end{array}
\begin{array} {c}
\text{equiv. of} \; MS_{\text{p}} \\
\left[ \begin{array} {rrr|r}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1}
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & +1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{+1} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}} \\
\left[ \begin{array} {rrr|r}
\frac{1}{\log_2(2)} & 0 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & 0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & +1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{+1} \\
\end{array} \right]
\end{array}
}[/math]
Multiply:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rr|r}
g_{1,1} & g_{1,2} & \style{background-color:#FFF200;padding:5px}{g_{1,\text{aug}}} \\
g_{2,1} & g_{2,2} & \style{background-color:#FFF200;padding:5px}{g_{2,\text{aug}}} \\
g_{3,1} & g_{3,2} & \style{background-color:#FFF200;padding:5px}{g_{3,\text{aug}}} \\
\hline
\style{background-color:#FFF200;padding:5px}{g_{\text{aug},1}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},2}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},\text{aug}}} \\
\end{array} \right]
\end{array}
\begin{array} {c}
\text{equiv. of} \; MS_{\text{p}}K \\
\left[ \begin{array} {rr|r}
2.262 & 2.292 & \style{background-color:#FFF200;padding:5px}{1} \\
{-1.892} & {-2.153} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{2} & \style{background-color:#FFF200;padding:5px}{2} & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}}K \\
\left[ \begin{array} {rr|r}
\frac{1}{\log_2(2)} & \frac{1}{\log_2(2)} & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
}[/math]
(Again, compare this with the minimax-S case. Same but augmented.) And now solve for [math]\displaystyle{ G }[/math]:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rr|r}
g_{1,1} & g_{1,2} & \style{background-color:#FFF200;padding:5px}{g_{1,\text{aug}}} \\
g_{2,1} & g_{2,2} & \style{background-color:#FFF200;padding:5px}{g_{2,\text{aug}}} \\
g_{3,1} & g_{3,2} & \style{background-color:#FFF200;padding:5px}{g_{3,\text{aug}}} \\
\hline
\style{background-color:#FFF200;padding:5px}{g_{\text{aug},1}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},2}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},\text{aug}}} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}}K \\
\left[ \begin{array} {rr|r}
\frac{1}{\log_2(2)} & \frac{1}{\log_2(2)} & \style{background-color:#FFF200;padding:5px}{1} \\
\frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} \\
\end{array} \right]
\end{array}
\begin{array} {c}
(\text{equiv. of} \; MS_{\text{p}}K)^{-1} \\
\left[ \begin{array} {rrr}
0 & 3.837 & 4.131 \\
0 & -3.837 & -3.632 \\
1 & 0.116 & -1.021 \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\\
\left[ \begin{array} {rr|r}
1 & 0.116 & \style{background-color:#FFF200;padding:5px}{-0.521} \\
0 & 2.421 & \style{background-color:#FFF200;padding:5px}{2.607} \\
0 & -1.652 & \style{background-color:#FFF200;padding:5px}{-1.564} \\
\hline
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{0.116} & \style{background-color:#FFF200;padding:5px}{-1.021} \\
\end{array} \right]
\end{array}
}[/math]
From that we can find [math]\displaystyle{ 𝒈 = 𝒋G }[/math]. But we need an augmented [math]\displaystyle{ 𝒋 }[/math] to do this. This will work:
[math]\displaystyle{
\left[ \begin{array} {rrr|r}
1200 & 1200 & 1200 & \style{background-color:#FFF200;padding:5px}{0} \\
\end{array} \right]
}[/math]
So that gives us [math]\displaystyle{ g_1 = 1200.000 }[/math], [math]\displaystyle{ g_2 = 138.930 }[/math], and [math]\displaystyle{ g_{\text{aug}} = -25.633 }[/math]. The last term is junk. As stated previously, it's only a side-effect of the computation process and isn't part of the useful result. Instead we only care about [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math], giving us the tuning {1200.000 138.930].
For this example we won't bother detailing all 8 candidate tunings. Too many. But we will at least note that not every tuning works out with an unchanged octave like this. And that this is not one of the better tunings; this one does about 26 ¢(S) damage, while half of the tunings are around only 3 ¢(S).
The best tuning we find from this set is {1193.828 161.900], and so that's our minimax-lils-S tuning of porcupine. We could compute this in the RTT Library in Wolfram Language with the following line of code:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "minimax-lils-S"]
Out: {1193.828 161.900]
Minimax-lols-S
This example specifically picks up from the setup laid out here: Dave Keenan & Douglas Blumeyer's guide to RTT/Alternative complexities#Log-odd-limit-squared2.
So for minimax-lols-S (AKA held-octave minimax-lils-S) we basically keep the same [math]\displaystyle{ MS_{\text{p}} }[/math] as before. But now (as discussed here) we have to further augment it with the mapped held-interval, [1 0 0⟩ (i.e. what the octave maps to in this temperament, including its augmented row, so that we can match it with its just size in the constrained linear system of equations to enforce it being held unchanged):
[math]\displaystyle{
\begin{array}{c}
\text{equiv. of} \; MS_{\text{p}} \\
\left[ \begin{array} {rrr|r|r}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1} \\
0 & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1} & \style{background-color:#00AEEF;padding:5px}{0} \\
\end{array} \right]
\end{array}
}[/math]
And as for our equivalent of [math]\displaystyle{ S_{\text{p}} }[/math], that's just going to be [math]\displaystyle{ L^{-1} }[/math] augmented first with the placeholder for the size dimension for the lil, and secondly with a placeholder for the just tuning of the held-interval which will appear in the augmented [math]\displaystyle{ 𝒋 }[/math] later, which will be matched up with its mapped form to ensure it is held unchanged.
[math]\displaystyle{
\left[ \begin{array} {rrr|r|r}
\frac{1}{\log_2(2)} & 0 & 0 & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} \\
0 & \frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} \\
0 & 0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#00AEEF;padding:5px}{0} \\
\hline
\style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1} \\
\end{array} \right]
}[/math]
Our list of [math]\displaystyle{ K }[/math]'s here is the same as the list for minimax-lils-S, but now they've all got one of their rows dedicated to holding the octave unchanged. For example the first one was:
[math]\displaystyle{
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#FFF200;padding:5px}{+1} \\
+1 & 0 & \style{background-color:#FFF200;padding:5px}{0} \\
0 & +1 & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{+1} \\
\end{array} \right]
}[/math]
But now it's:
[math]\displaystyle{
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#8DC73E;padding:5px}{0} \\
+1 & 0 & \style{background-color:#8DC73E;padding:5px}{0} \\
0 & +1 & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1}
\end{array} \right]
}[/math]
(To explain the green highlighting: those cells are pertinent to both augmentations. The yellow part of the green indicates that the lil-augmentation put a new column there at all. The blue indicates that now that column has been replaced with a column for holding an interval unchanged. The held-octave issue did not actually add a new column here, only a new row.)
So let's just work through one tuning with the first [math]\displaystyle{ K }[/math]. Note that [math]\displaystyle{ 𝒈 }[/math] is augmented as it was for the minimax-lils-S computation. Applying the constraint to get an equality:
[math]\displaystyle{
\scriptsize
\begin{array} {c}
G \\
\left[ \begin{array} {rr|r}
g_{1,1} & g_{1,2} & \style{background-color:#FFF200;padding:5px}{g_{1,\text{aug}}} \\
g_{2,1} & g_{2,2} & \style{background-color:#FFF200;padding:5px}{g_{2,\text{aug}}} \\
g_{3,1} & g_{3,2} & \style{background-color:#FFF200;padding:5px}{g_{3,\text{aug}}} \\
\hline
\style{background-color:#FFF200;padding:5px}{g_{\text{aug},1}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},2}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},\text{aug}}} \\
\hline
\style{background-color:#00AEEF;padding:5px}{g_{\text{held},1}} & \style{background-color:#00AEEF;padding:5px}{g_{\text{held},2}} & \style{background-color:#8DC73E;padding:5px}{g_{\text{held},\text{aug}}} \\
\end{array} \right]
\end{array}
\begin{array}{c}
\text{equiv. of} \; MS_{\text{p}} \\
\left[ \begin{array} {rrr|r|r}
\frac{1}{\log_2(2)} & \frac{2}{\log_2(3)} & \frac{3}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1} \\
0 & \frac{-3}{\log_2(3)} & \frac{-5}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#FFF200;padding:5px}{-1} & \style{background-color:#00AEEF;padding:5px}{0} \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#8DC73E;padding:5px}{0} \\
+1 & 0 & \style{background-color:#8DC73E;padding:5px}{0} \\
0 & +1 & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1}
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}} \\
\left[ \begin{array} {rrr|r|r}
\frac{1}{\log_2(2)} & 0 & 0 & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} \\
0 & \frac{1}{\log_2(3)} & 0 & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} \\
0 & 0 & \frac{1}{\log_2(5)} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{1} & \style{background-color:#00AEEF;padding:5px}{0} \\
\hline
\style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1} \\
\end{array} \right]
\end{array}
\begin{array} {c}
K \\
\left[ \begin{array} {rr|r}
+1 & +1 & \style{background-color:#8DC73E;padding:5px}{0} \\
+1 & 0 & \style{background-color:#8DC73E;padding:5px}{0} \\
0 & +1 & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1}
\end{array} \right]
\end{array}
}[/math]
Multiply:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rr|r}
g_{1,1} & g_{1,2} & \style{background-color:#FFF200;padding:5px}{g_{1,\text{aug}}} \\
g_{2,1} & g_{2,2} & \style{background-color:#FFF200;padding:5px}{g_{2,\text{aug}}} \\
g_{3,1} & g_{3,2} & \style{background-color:#FFF200;padding:5px}{g_{3,\text{aug}}} \\
\hline
\style{background-color:#FFF200;padding:5px}{g_{\text{aug},1}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},2}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},\text{aug}}} \\
\hline
\style{background-color:#00AEEF;padding:5px}{g_{\text{held},1}} & \style{background-color:#00AEEF;padding:5px}{g_{\text{held},2}} & \style{background-color:#8DC73E;padding:5px}{g_{\text{held},\text{aug}}} \\
\end{array} \right]
\end{array}
\begin{array} {c}
\text{equiv. of} \; MS_{\text{p}}K \\
\left[ \begin{array} {rr|r}
2.262 & 2.292 & \style{background-color:#FFF200;padding:5px}{1} \\
{-1.892} & {-2.153} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#8DC73E;padding:5px}{2} & \style{background-color:#8DC73E;padding:5px}{2} & \style{background-color:#8DC73E;padding:5px}{0} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}}K \\
\left[ \begin{array} {rr|r}
\frac{1}{\log_2(2)} & \frac{1}{\log_2(2)} & \style{background-color:#8DC73E;padding:5px}{0} \\
\frac{1}{\log_2(3)} & 0 & \style{background-color:#8DC73E;padding:5px}{0} \\
0 & \frac{1}{\log_2(5)} & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1} \\
\end{array} \right]
\end{array}
}[/math]
Solve for [math]\displaystyle{ G }[/math]:
[math]\displaystyle{
\begin{array} {c}
G \\
\left[ \begin{array} {rr|r}
g_{1,1} & g_{1,2} & \style{background-color:#FFF200;padding:5px}{g_{1,\text{aug}}} \\
g_{2,1} & g_{2,2} & \style{background-color:#FFF200;padding:5px}{g_{2,\text{aug}}} \\
g_{3,1} & g_{3,2} & \style{background-color:#FFF200;padding:5px}{g_{3,\text{aug}}} \\
\hline
\style{background-color:#FFF200;padding:5px}{g_{\text{aug},1}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},2}} & \style{background-color:#FFF200;padding:5px}{g_{\text{aug},\text{aug}}} \\
\hline
\style{background-color:#00AEEF;padding:5px}{g_{\text{held},1}} & \style{background-color:#00AEEF;padding:5px}{g_{\text{held},2}} & \style{background-color:#8DC73E;padding:5px}{g_{\text{held},\text{aug}}} \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\text{equiv. of} \; S_{\text{p}}K \\
\left[ \begin{array} {rr|r}
\frac{1}{\log_2(2)} & \frac{1}{\log_2(2)} & \style{background-color:#8DC73E;padding:5px}{0} \\
\frac{1}{\log_2(3)} & 0 & \style{background-color:#8DC73E;padding:5px}{0} \\
0 & \frac{1}{\log_2(5)} & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#8DC73E;padding:5px}{0} \\
\hline
\style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1} \\
\end{array} \right]
\end{array}
\begin{array} {c}
(\text{equiv. of} \; MS_{\text{p}}K)^{-1} \\
\left[ \begin{array} {rrr}
0 & 3.838 & 4.132 \\
0 & -3.838 & -3.632 \\
1 & 0.116 & -1.021 \\
\end{array} \right]
\end{array}
=
\begin{array} {c}
\\
\left[ \begin{array} {rr|r}
0 & 0 & \style{background-color:#FFF200;padding:5px}{0.500} \\
0 & 2.421 & \style{background-color:#FFF200;padding:5px}{2.607} \\
0 & -1.653 & \style{background-color:#FFF200;padding:5px}{-1.564} \\
\hline
\style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#FFF200;padding:5px}{0} \\
\hline
\style{background-color:#00AEEF;padding:5px}{1} & \style{background-color:#00AEEF;padding:5px}{0.116} & \style{background-color:#8DC73E;padding:5px}{-1.021} \\
\end{array} \right]
\end{array}
}[/math]
From that we can find [math]\displaystyle{ 𝒈 = 𝒋G }[/math]. But we need to have augmented [math]\displaystyle{ 𝒋 }[/math] accordingly. It needs to be augmented both for the lils and for the held-octave. Specifically, for the held-octave, we need to add its just tuning in cents. So that's 1200. It works out to:
[math]\displaystyle{
\left[ \begin{array} {rrr|r|r}
1200 & 1200 & 1200 & \style{background-color:#FFF200;padding:5px}{0} & \style{background-color:#00AEEF;padding:5px}{1200} \\
\end{array} \right]
}[/math]
So we find [math]\displaystyle{ g_1 = 1200 }[/math], [math]\displaystyle{ g_2 = 138.930 }[/math], and [math]\displaystyle{ g_{\text{aug}} = -25.633 }[/math]. As stated previously, the result for [math]\displaystyle{ g_{\text{aug}} }[/math] is just a side-effect of the computation process and isn't part of the useful result. Instead we only care about [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math], giving us the tuning {1200.000 138.930]. (Yes, that's the same tuning as we found for minimax-lils-S; it happens that the octave was already pure for that one, and otherwise nothing about the tuning scheme changed.)
For this example we won't bother detailing all 8 candidate tunings. Too many. But we will at least note that not every tuning works out with a held octave like this. And that this is not one of the better tunings; this one does about 26 ¢(S) damage, while half of the tunings are around only 3 ¢(S).
The best augmented tuning we find from this set is [1200 162.737 -3.102], and so that's our held-octave minimax-lols-S tuning of porcupine. Well, when you throw away that [math]\displaystyle{ g_{\text{aug}} }[/math] final entry anyway, to get {1200 162.737].
We could compute this in the RTT Library in Wolfram Language with the following line of code:
In: optimizeGeneratorTuningMap["[⟨1 2 3] ⟨0 -3 -5]]", "held-octave minimax-lols-S"]
Out: {1200 162.737]
Footnotes
- ↑ Gene Ward Smith discovering this relationship: https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_16172#16172
- ↑ The actual answer is more like 100.236. The result here is due to compounding rounding errors that I was too lazy to account for when preparing these materials. Sorry about that. ~Douglas
- ↑ Ideally we'd've consistently applied the Fraktur-styling effect to each of these letters, changing no other properties, i.e. ended up with an uppercase italic M and lowercase bold italic j and t, but unfortunately a consistent effect was not available using Unicode and the wiki's [math]\displaystyle{ \LaTeX }[/math] abilities, a consistent effect, anyway, that also satisfactorily captured the compound aspect of what these things represent.
- ↑ Perhaps re-running this process in the recognition of the fact that these matrices are shorthand for an underlying system of equations, and the derivative of [math]\displaystyle{ 𝒈 }[/math] is, in fact, its gradient, or in other words, the vector of partial derivatives with respect to each of its entries (as discussed in more detail in the later section, #Multiple derivatives), we could nail this down.
- ↑ If you don't dig it, please consider alternative attempts to explain these ideas here: User:Sintel/Generator_optimization#Constraints, here: Constrained_tuning/Analytical_solution_to_constrained_Euclidean_tunings, and here: Target tuning#Least squares tunings
- ↑ This is a different lambda to the one conventionally used for eigenvalues, or as we call them, scaling factors. This lambda refers to Lagrange, the mathematician who developed this technique.
- ↑ To help develop your intuition for these sorts of problems, we recommend Grant Sanderson's series of videos for Khan Academy's YouTube channel, about Lagrange multipliers for constrained optimizations: https://www.youtube.com/playlist?list=PLCg2-CTYVrQvNGLbd-FN70UxWZSeKP4wV
- ↑ See https://en.m.wikipedia.org/wiki/Lagrange_multiplier#Multiple_constraints for more information.
- ↑ [math]\displaystyle{ \begin{align} \begin{array} {c} 𝔐 \\ \left[ \begin{array} {c} 𝕞_{11} & 𝕞_{12} \\ 𝕞_{21} & 𝕞_{22} \\ \end{array} \right] \end{array} \begin{array} {c} 𝔐^\mathsf{T} \\ \left[ \begin{array} {c} 𝕞_{11} & 𝕞_{21} \\ 𝕞_{12} & 𝕞_{22} \\ \end{array} \right] \end{array} &= \\[12pt] \begin{array} {c} 𝔐𝔐^\mathsf{T} \\ \left[ \begin{array} {c} 𝕞_{11}^2 + 𝕞_{12}^2 & 𝕞_{11}𝕞_{21} + 𝕞_{12}𝕞_{22} \\ 𝕞_{11}𝕞_{21} + 𝕞_{12}𝕞_{22} & 𝕞_{21}^2 + 𝕞_{22}^2 \\ \end{array} \right] \end{array} &∴ \\[12pt] (𝔐𝔐^\mathsf{T})_{12} = (𝔐𝔐^\mathsf{T})_{21} \end{align} }[/math]
- ↑ Writes the present author, Douglas Blumeyer, who is relieved to have completely demystified this process for himself, after being daunted by it for over a year, then struggling for a solid week to assemble it from the hints left by the better-educated tuning theorists who came before me.
- ↑ Another reason we wrote the method for this optimization power up is because it was low-hanging fruit, on account of the fact that it was already described on the wiki in the Target tunings page, where it is presented as a method for finding "minimax" tunings, not miniaverage tunings. This is somewhat misleading, because while this method works for any miniaverage tuning scheme, it only works for some minimax tuning schemes under very specific conditions (which that page does meet, and so it's not outright wrong). The conditions are: unity-weight damage (check), and all members of the target-interval set expressible as products of other members (check, due to their choice of target-interval set, closely related to a tonality diamond, plus octaves are constrained to be unchanged). The reason why these are the two necessary conditions for this miniaverage method working for a minimax tuning scheme is because when you are solving for the minimax, you actually want the tunings where the target-intervals' damages equal each other, not where they are zero, and these zero-damage tunings will only match the tunings where other intervals' damages equal each other in the case where two intervals' damages being equal implies that another target's damage is zero, because that other target is the product of those first two; and the unity-weight damage requirement is to ensure that the slopes of each target's hyper-V are all the same, because otherwise the points where two damages are equal like this will no longer line up directly over the point where the third target's damage is zero. For more information on this problem, please see the discussion page for the problematic wiki page, where we are currently requesting the page be updated accordingly.
- ↑ Note that this technique for converting zero-damage points to generator tunings is much simpler than the technique described on the Target tunings page. The Target tunings page uses eigendecomposition, which unnecessarily requires you to find the commas for the temperament, compute a full projection matrix [math]\displaystyle{ P }[/math], and then when you need to spit a generator tuning map [math]\displaystyle{ 𝒈 }[/math] out at the end, requires the computation of a generator detempering to do so (moreover, it doesn't explain or even mention eigendecomposition; it assumes the reader knows how and when to do them, cutting off at the point of listing the eigenvectors—a big thanks to Sintel for unpacking the thought process in that article for us). The technique described here skips the commas, computing the generator embedding [math]\displaystyle{ G }[/math] directly rather than via [math]\displaystyle{ P = GM }[/math], and then when you need to spit a generator tuning map out at the end, it's just [math]\displaystyle{ 𝒈 = 𝒋G }[/math], which is much simpler than the generator detempering computation.
The Target tunings approach and this approach are quite similar conceptually. Here's the Target tunings approach:
[math]\displaystyle{ \scriptsize \begin{array} {c} P \\ \left[ \begin{array} {rrr} 1 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & \frac14 & 1 \\ \end{array} \right] \end{array} = \\ \scriptsize \begin{array} {c} \mathrm{V} \\ \left[ \begin{array} {r|r|r} \style{background-color:#98CC70;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#F2B2B4;padding:5px}{-4} \\ \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#F2B2B4;padding:5px}{4} \\ \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{1} & \style{background-color:#F2B2B4;padding:5px}{-1} \\ \end{array} \right] \end{array} \begin{array} {c} \textit{Λ} \\ \left[ \begin{array} {rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} \right] \end{array} \begin{array} {c} \mathrm{V} \\ \left[ \begin{array} {r|r|r} \style{background-color:#98CC70;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#F2B2B4;padding:5px}{-4} \\ \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#F2B2B4;padding:5px}{4} \\ \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{1} & \style{background-color:#F2B2B4;padding:5px}{-1} \\ \end{array} \right]^{{\Large-1}} \end{array} }[/math]
And the technique demonstrated here looks like this:
[math]\displaystyle{ \scriptsize \begin{array} {c} G \\ \left[ \begin{array} {rrr} 1 & 1 \\ 0 & 0 \\ 0 & \frac14 \\ \end{array} \right] \end{array} = \\ \scriptsize \begin{array} {c} \mathrm{U} \\ \left[ \begin{array} {r|r} \style{background-color:#98CC70;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{0} \\ \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} \\ \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{1} \\ \end{array} \right] \end{array} \Large ( \scriptsize \begin{array} {c} M \\ \left[ \begin{array} {rrr} 1 & 0 & {-4} \\ 0 & 1 & 4 \\ \end{array} \right] \end{array} \begin{array} {c} \mathrm{U} \\ \left[ \begin{array} {r|r} \style{background-color:#98CC70;padding:5px}{1} & \style{background-color:#98CC70;padding:5px}{0} \\ \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{0} \\ \style{background-color:#98CC70;padding:5px}{0} & \style{background-color:#98CC70;padding:5px}{1} \\ \end{array} \right] \end{array} \Large )^{-1} \scriptsize }[/math]
So in the Target tunings approach, [math]\displaystyle{ P }[/math] is the projection matrix, [math]\displaystyle{ \mathrm{V} }[/math] is a matrix consisting of a list of unrotated vectors—both ones with scaling factor 1 (unchanged-intervals) and those with scaling factor 0 (commas)—and [math]\displaystyle{ \textit{Λ} }[/math] is a diagonal scaling factors matrix, where you can see along the main diagonal we have 1's paired with the unrotated vectors for unchanged-intervals and 0's paired with the unrotated vectors for commas.
In our approach, we instead solve for [math]\displaystyle{ G }[/math] by leaving the commas out of the equation, and simply using the mapping [math]\displaystyle{ M }[/math] instead.
In addition to being much more straightforward and easier to understand, our technique gives the same results and reduces computation time by 50% (it took the computation of a miniaverage-U tuning for a rank-3, 11-limit temperament with 15 target-intervals from 12 seconds down to 8). - ↑ Technically this gives us the tunings of the generators, in ¢/g.
- ↑ The article for the minimax tuning scheme, Target tunings, suggests that you fall back to the miniRMS method to tie-break between these, but that sort of misses the point of the problem. The two tied points are on extreme opposite ends of the slice of good solutions, and the optimum solution lies somewhere in between them. We don't want the tie-break to choose one or the other extreme; we want to find a better solution somewhere in between them.
- ↑ There does not seem to be any consensus about how to identify a true optimum in the case of multiple solutions when [math]\displaystyle{ p=1 }[/math]. See https://en.wikipedia.org/wiki/Least_absolute_deviations#Properties, https://www.researchgate.net/publication/223752233_Dealing_with_the_multiplicity_of_solutions_of_the_l1_and_l_regression_models, and https://stats.stackexchange.com/questions/275931/is-it-possible-to-force-least-absolute-deviations-lad-regression-to-return-the.
- ↑ In fact, the Target tunings page of the wiki uses this more complicated approach in order to realize pure octaves, and so the authors of this page had to reverse engineer from it how to make it work without any held-intervals.
- ↑ Held-intervals should generally be removed if they also appear in the target-interval list [math]\displaystyle{ \mathrm{T} }[/math]. If these intervals are not removed, the correct tuning can still be computed; however, during optimization, effort will have been wasted on minimizing damage to these intervals, because their damage would have been held to 0 by other means anyway. In general, it should be more computationally efficient to remove these intervals from [math]\displaystyle{ \mathrm{T} }[/math] in advance, rather than submit them to the optimization procedures as-is. Duplication of intervals between these two sets will most likely occur when using a target-interval set scheme (such as a TILT or OLD) that automatically chooses the target-interval set.
- ↑ See https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_20405.html and https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_21022.html
- ↑ were everything transposed, anyway; a superficial issue
- ↑ This weight is irrelevant, since these aren't really target-intervals, they're held-intervals, and so the damage to them must be 0; we can choose any value for this weight other than 0 and the effect will be the same, so we may as well choose 1).
- ↑ You may be unsurprised to learn that this example of basic tie-breaking success was actually developed from the case that requires advanced tie-breaking, i.e. by adding [math]\displaystyle{ \frac65 }[/math] to the target-interval set in order to produce the needed point at the true minimax, rather than the other way around, that the advanced tie-breaking case was developed from the basic example.
- ↑ note that we can't rely on which half of the V-shaped graph we're on to tell whether a damage corresponds with a positive or negative error; that depends on various factors relating to [math]\displaystyle{ 𝒈 }[/math], [math]\displaystyle{ M }[/math], and the ties
- ↑ https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_20405.html#20412
- ↑ https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_20405.html#20412
- ↑ https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_21029.html