Mike Sheiman's Very Easy Scale Building From The Harmonic Series Page
The diatonic scale under 12EDO (also simply known as C Major on a standard piano) is largely developed from the idea of keeping simple intervals fairly pure. Here I will explain what these simple intervals are, how they work, and how to derive the diatonic scale in a very pure, consonant form. Then I will use it to explain a harmonious Middle-Eastern type of scale, then use the same idea to very quickly make your own very harmonious, original sounding scales with very few "wolf" dissonances and many perfectly pure (not approximated or "tempered") intervals.
If you want to jump in and just start playing music with the scales on a/your Android phone or tablet, try this software.
For an version using a revised update of this theory, look at this
If your main gripe with microtonal music is that it sounds unnatural or dissonant...the basis for this is just as harmonious, if not more so, than the 7-tone diatonic scale you normally use on your 12 tone (12EDO) keyboard or guitar at home.
Perhaps best of all...to learn this you will need nothing but early to middle grade school level multiplication and division with pure fractions!
How can this be done so easily? Probably the simplest structure in microtonality, and the most relaxed/natural sounding and native to the human ear, is the harmonic series. The unison is 1/1, the octave is 2/1...and further parts of the harmonic series are simply 3/1, 4/1, 5/1...
Purity in Just Intonation often has a connection with small numbered ratios low in the harmonic series. So 3/2 (the fifth), 4/3 (the fourth), 5/3 (the sixth), and 5/4 (the third) are among the most consonant and relaxed sounding in music and these form the basis of the diatonic scale. And by "Just ratios" I simply mean "using numbers low in the harmonic series" or simply "using low numbered fractions".
Now how do we make an entire scale keep as many notes as possible at Just ratios from each other? One way is to try and find numbers with as many low common factors as possible.
What makes a common factor (AKA as part of a Least Common Multiple)? For example 3 is a factor of 12 because it can be multiplied by another whole number (4) to get 12. 4 is a factor because multiply by 3 gives 12. And 2 and 6 are factors because 2 * 6 = 12. As you can see...this is nothing more than early grade school math.
Here are some numbers with a lot of factors:
- For the LCM of 12 the factors include 2, 3, 4 and 6...all these factors are multiples of the primes 2 or 3.
- For 18 the factors include 2, 3, 6 and 9. Again, all these factors are multiples of 2 or 3.
- For 24 the factors include 2, 3, 4, 6, 8 and 12. Yet again, all these factors are multiples of 2 or 3 (go figure as well, the fifth in modern music theory is 3/2).
- For 30 the factors include 2, 3, 5, 6, 10 and 15. Note how much less factors per size of number (30) you have available when you include the mid-sized prime 5 as a factor...6 of 30 (6/30 = 1/5) instead of 6 of 24 (6/24 = 1/4).
- For 28 the factors are 2, 4, 7 and 14. Note how much fewer factors are available when you use the higher prime of 7.
First, let's try and explain how the basic 7-tone diatonic mode in 12EDO works. Consider the number 24 (#3 above). For a scale with 24 partials that fits the 2/1 octave...you get numbers 24 to 48 to use in your scale (note the 2/1 octave times 24 is 48).
Now let's try to pick numbers between 24 and 48 that have as many low common factors as possible.
24 (factors 2,3,4,6,8)
27 (factors 3, 9)
30 (factors 2,3, 5, 6)
32 (factors 2,4,8)
36 (factors 2,3,4,6,9)
40 (factors 2,4,5,8)
45 (factors 3,5,9)
48 (factors 2,3,4,6,8)
Notice the ratios in this scale (the 24 in the denominator is the root AKA "C")
The 7 tone diatonic scale (virtually the same as "C Major" on your keyboard)
24/24 = 1/1 (C)
27/24 = 9/8 (D)
30/24 = 5/4 (E)
32/24 = 4/3 (F)
36/24 = 3/2 (G)
40/24 = 5/3 (A)
45/24 = 15/8 (B)
48/24 = 2/1 (C)
These are the exact same ratios used in the Just Intonation diatonic scale... which C major is virtually the same as! (But see the appendix for a possible caveat.)
Plus, many of the chords sound more pure and relaxed. Note 1/1 5/4 and 3/2 form 4/4 5/4 6/4 AKA 4:5:6...a perfectly pure C major chord...and 5/4 3/2 15/8 form a 10/8 12/8 15/8 AKA 10:12:15 chord...are perfectly pure. Again, this is all just by using fractions and finding numbers with many low common factors).
An alternative example of the 24th harmonic in action (not related to the diatonic scale) I ran into while trying Porcupine Temperament is
Modified Porcupine Scale
24/24 = 1/1
26/24 = 13/12
28/24 = 7/6
30/24 = 5/4
33/24 = 11/8 (optional)
36/24 = 3/2
40/24 = 5/3 (edited from 41/24 on 11/02/12)
44/24 = 11/6
48/24 = 2/1
This one has a few anomalies: it has "alien" notes/intervals such as 13/12, 7/6, 11/8, and 11/6 that are nowhere near notes in the diatonic system. However, try writing a melody or chord progression in it and you'll likely be surprised how relaxed it sounds despite having such intervals. This suggests the mind may indeed be hard-wired to more easily digest/summarize systems reduce-able to the denominator 24 or under.
Now that we have explained the basic diatonic scale in basic fractions and, to an extent, showed that the human mind/ear generally likes scale simplify-able to fairly low denominators AKA harmonic series segments...let's make a basic Arabic scale using 18. Note we will use a few numbers which have slightly less common factors, and less purity, in order to get a more fresh/original sound than diatonic
Middle Eastern / Blues scale based on the number 18
18/18 = 1/1 (C)
20/18 = 10/9 (a bit below D)
22/18 = 11/9 (E neutral)
24/18 = 4/3 (F) 8
27/18 = 3/2 (G) 9
30/18 = 5/3 (A)
33/18 = 11/6 (B neutral) 11
36/18 = 2/1 (C)
Note the new 11/6 (neutral seventh) and 11/9 (neutral third) fractions...these are called "neutral intervals", right between the major and minor third and seventh intervals. Such intervals are often used in Blues (called "blue tones") and Middle-Eastern music. But they are still very useful for beautiful chords. For example, try a 1/1 11/9 15/9 chord with C, E neutral, and A. Or F G B-neutral (4/3 3/2 11/6 = 8/6 9/6 11/6 = 8:9:11).
You might ask, why not use 32 (factors 2, 4, 8) instead of 33 (factors 3 and 11) in 33/18 above....or 21 (factors 3 and 7) instead of 22 (factor 2 and 11) in 22/18 above? You lose those "blue tones"...but, given the increase in common factors and/or lower common factors, you are likely to find more chords you can use musically as resolved/relaxed/consonant points.
It also turns out you can combine the Middle Eastern scale and 7-tone diatonic scale into a 9-tone scale system I call "Dimension", which features the neutral third and seventh from the blues and Maqam Rast Middle Eastern scale systems.
The "Dimension" scale is listed under 31edo modes.
A musical example of the "Dimension" scale in use is available here
For the 12th harmonic, you can get something even more fresh/different sounding, but still quite natural and consonant
12th Harmonic Scale
12/12 = 1/1
14/12 = 7/6
15/12 = 5/4
16/12 = 4/3
18/12 = 3/2
20/12 = 5/3
21/12 = 7/4
24/12 = 2/1
To hear a musical sound sample of this scale, listen to
Of course, 22 has a few factors (2 and 11)...and 21 (factors 3 and 7) has no more factors than 22 does.
So you can get a different scale with comparable harmoniousness by swapping 21 and 22 to get
12th Harmonic Scale (modified) AKA "6 factor" scale
12/12 = 1/1
14/12 = 7/6
15/12 = 5/4
16/12 = 4/3
18/12 = 3/2
20/12 = 5/3
22/12 = 11/6 (changed from 7/4)
24/12 = 2/1
To hear a musical sound sample of this scale, listen to
Lucy In The Sky With Dreams (retuned)
You can get more than one scale per number (IE multiple scales for "12")...but to get the scales with the most harmonic options, stick with numbers with many factors.
For example, 13/12 would not be a good choice, as 13 is prime and only has itself (13) as a factor. This gives you chords like 13/12 16/12 18/12 = 13:16:18, which often do not sound very harmonious.
Using low numbered fractions with many low common factors will simply lessen the chance you will get high-numbered intervals AKA "Wolf" intervals, which sound very tense. You will get them with this method, but usually very few of them. You can often use tempering to help correct the wolf intervals...as described below.
As a final note, you can use a method of making a scale using a fraction with both numerators and denominators with many factors as a basis.
An example of a scale system using that property is Erv Wilson's 6-tone "Hexany" scale. This scale includes a fairly dissonant sounding 35/24 in it, but the fact that 35 has 7 and 5 as factors and 24 has 2, 3, 4, 6,and 8 as factors makes this seemingly odd fraction work well with the other tones to form very harmonious chords (specifically triads AKA "three note chords").
Erv Wilson's 6-tone "Hexany" scale
24/24 = 1/1
28/24 = 7/6
30/24 = 5/4
35/24 = 35/24 (not able to be reduced)
40/24 = 5/3
42/24 = 7/4
48/24 = 2/1
For an excellent musical example of this scale, listen to Marcus Satellite’s track here
The same trick can be used to make larger scales. In this case, I take 45/28 (45 with factors 3, 5, 9 and 28 with factors 2, 4, and 7) and use it to connect to a 28th harmonic scale. Despite its large size, it by and large avoids dissonant sounding "wolf" intervals.
28th Harmonic Scale (9 tones)
28 1/1
30 15/14
35 5/4
36 9/7
40 10/7
42 3/2
45 45/28 about 8/5
48 12/7 (forms wolf tone of almost exactly 16/11 between 12/7 and 5/4)
50 50/28 (near 16/9)
56 2/1
28th Harmonic Scale Second Type (8 tones)
28 1/1
30 15/14
32 8/7
36 9/7
40 10/7
45 45/28 about 8/5
48 12/7
50 50/28 (near 16/9)
56 2/1
Note: Paul Erlich showed me, by mapping on a lattice, this scale can further be improved by adding a 49/28 (7/4) and an 32/28 (8/7) and even a 15/8 (which does not fit on the 28th harmonic at all). This marks the fact that, on a higher mathematical level, these scales can be further improved by using analysis through lattices.
28th Harmonic Scale 12-tone version by Paul Erlich (12 tones, additional notes not in either of my original scales are in bold)
28 1/1
30 15/14
32 8/7
35 5/4
36 9/7
40 10/7
42 3/2
45 45/28 about 8/5
48 12/7 (forms wolf tone of almost exactly 16/11 between 12/7 and 5/4)
49 49/28
50 50/28 (near 16/9)
(52.5)---------15/8 (not within 28th harmonic)
56 2/1
Note: a 4/3 can be added to this as well, under the 8/7 and beside the 1/1.
For a musical example of this scale in action you can try this 6 minute long piece: The Ghost of Max
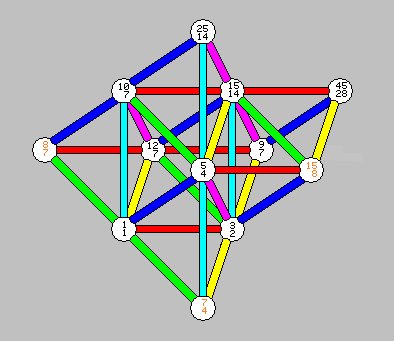
Scale Diagram/Lattice below
30th Harmonic Scale (factors 2,3,5,6)
30/30 1/1
32/30 16/15
36/30 6/5
40/30 4/3
45/30 3/2
48/30 8/5
50/30 5/3
Appendix for people who don't like wolf intervals
It was said above that the JI scale 1/1, 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, 2/1 was similar to the diatonic major scale. If we take 1/1 as C, it's like C major. However, there is an important difference between this JI scale and the C major scale most people are used to.
In the C major scale, the interval between D and A is a good perfect fifth; that is to say, a good approximation of 3/2. However, in this JI scale, the interval between 9/8 and 5/3 is not 3/2. Instead it is the much more complex interval 5/3 / (9/8) = 40/27, which is a very narrow fifth. Although the scale is "just intonation", meaning all the intervals are exact rational numbers, it's basically impossible to recognize 40/27 as the specific JI interval 40/27; for most people it sounds like a 3/2 perfect fifth that is badly out of tune. (And even if some superhuman listener could recognize it as an exact 40/27, it's weird that this D-A interval should be different from the similar intervals from C-G, G-D etc., which are normally treated as equivalent.) This weird interval is known as a "wolf fifth".
Getting rid of this wolf fifth is not simple. For example, you might think to change one of the pitches D or A in order to make D-A a correct 3/2 perfect fifth. But if you change D that will mess up the fifth G-D, and if you change A that will mess up the fifth A-E. You're simply moving the wolf around rather than getting rid of it. Also, if you keep changing pitches until you eventually arrive at an interval that's not close to 3/2, so that all the fifths in the chain F-C-G-D-A-E-B are 3/2s, then you now have a Pythagorean scale, which has much more complicated intervals than the simple JI scale you started with. For example, all the major thirds in this scale are 81/64 rather than 5/4.
To get rid of the wolf fifth and arrive at a C major scale that really has all the familiar properties, you have to temper the scale, which means spreading out the error of the wolf fifth over many fifths so that, although none of them are exactly a 3/2 ratio, they are all good approximations. With modern technology and temperament theory, this is an easy process.
- First, look for wolf intervals in your scale. In this case we already know one: the interval from D-A is 40/27, but we want it to be (approximately) 3/2 like all the other perfect fifths.
- Next, calculate the difference (the "comma") between the wolf interval and the interval you want it to represent. In this case the difference is 3/2 / (40/27) = 81/80, the well known syntonic comma. This represents the error intrinsic to the diatonic scale as it's actually used, and we would like it to disappear.
- Now, put the comma in the box in Graham Breed's temperament finder. It will spit out a list of temperaments that "temper out" that comma, which makes it possible for the scale to work as you want it to with no wolf intervals. In this case there is only one temperament, the well-known Meantone temperament, whose generator is a slightly narrow 3/2.
- Finally, use the information it gives you to write down your scale in the appropriate temperament. One way to do this is to use the period and generator it gives you, in this case 1201.397 and 504.348 cents. All the notes of your scale can be arrived at by adding and subtracting these the appropriate number of times.
- If there appear to be any more wolf intervals, go back to the first step and repeat, making sure to keep all the commas from earlier steps.
The result of doing this for the C major scale is the meantone C major scale, which, rounded to the nearest cent, is:
0 193 385 503 697 889 1082 1201
If you try this scale out, you will find it to be free of wolf intervals, yet still as close to JI as possible.
"Middle Eastern / Blues scale"
If you apply this procedure to the "Middle Eastern / Blues scale" above, you find that it also contains 40/27, so a wolf-free version will also temper out 81/80. However, in this case even if you temper out 81/80 there are other wolf intervals that still remain, in particular 27/22, which is very close to the simplest possible neutral third, 11/9. Tempering out this comma, 243/242, in addition to 81/80, leads to mohajira temperament and this version of the scale:
0 193 349 505 697 890 1046 1202
Since the pattern of intervals is LssLLss rather than LssLsLs, this is a MODMOS of mohajira. Specifically, it's the "maqam rast" MODMOS, a mode used in Middle Eastern music.
"12th harmonic scales" and note about personal preference
The first 12th harmonic scale has, debatably, only one interval that falls into the "wolf" category: the 21/16 interval appearing between 4/3 and 7/4 (the second 12th harmonic scale has basically no wolf intervals). If you desired to use this interval as 4/3 you could temper out the comma 64/63 and obtain:
0 271 392 489 708 882 979 1197
However, there are also good reasons you wouldn't want to do this: the comma 64/63 is relatively large and tempering it out introduces many cents worth of error, and some might enjoy the sound of 21/16 itself (being not quite unreasonably complex).
Of course, all of these temperament ideas are merely suggestions, and anyone is free to use any version of a scale they feel like. The choice ultimately comes down to what you find most desirable in a scale: If you demand that certain intervals be exact JI consonances, and don't mind that not all intervals are uniformly simple (i.e. don't mind wolves), then JI scales are for you. But if you want the freedom to play any note that seems like it should be a consonance and have it actually be that consonance (not off by a comma), then temperament is your friend.