Expanding tonal space/third dimension

< Expanding tonal space

This is Part IV of a small series of articles discussing the model of tonal space.
On this subpage, we will discuss the extension of the model (see Part I) to three dimensions.

Terminology

Before we discuss the third dimension of Tonal Space and take a look at adaptive just intonation, we need to clarify the meaning of some terms:
The Xenharmonic Wiki redirects the term Tonal center to the page Tonic, which apparently means that both terms are equivalent. On the page Root we read that root is used interchangeably with tonic:

“The term root is sometimes used to refer to the central establishing pitch which all other pitches are perceived in relation to. It is used interchangeably with "tonic". ”

Thus in the context of the model of tonal space we prefer the term tonic and use it interchangeably with tonal center and root.

3-dimensional extension of tonal space

Fig.1: View of 3D-tonal space with the dimension of tonic ([math]\displaystyle{ u }[/math])

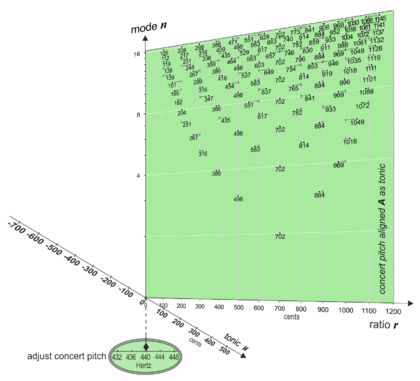
The purpose of the consideration of tonal space is the design of a musical instrument with dynamic intonation control.

Although the focus remains on creating chords from modes of the overtone scale, a certain degree of compatibility with instruments tuned in twelve-tone equal temperament (12edo) is desirable for free modulation. This is demonstrated in the following three use cases.

As we will see, the desire to integrate equally tempered pitches is addressed by introducing a third dimension to the model, the dimension of the tonic ([math]\displaystyle{ u }[/math]).

Use Case 1: Teaching the Pierce College Jazz Choir

We begin with a practical example where the tonics are taken from the static 12edo tuning of a piano, and the intervals above the tonic are justly intonated. Jazz choir director Gerald Eskelin shares his experience with 12edo tonics. The adaptive just tuning is not controlled by an algorithm but by well-trained singers:

“It wasn’t until I was teaching the Pierce College Jazz Choir that I realized how detrimental the piano was to developing accurate pitch concepts. (…)

Fig.2: Swingin', The Pierce College Jazz Choir, 1979

So, I suggested to Dwight, our accompanist, to play only the roots as we sang our up-a-fifth warm-ups. This exercise was very beneficial in demonstrating what “in tune” really meant. When fifths were secure, we moved on to other intervals until the singers could make a minor second (half step) sparkle like a musical diamond. (…) So with Dwight’s help, we weaned our Pierce College Jazz Choir singers away from tempered tuning. When we tuned chords, he played only the root note and allowed the singer to find the place where the notes locked into place.”

According to this use case, we will incorporate additional planes into the model that allow us to align an arbitrary single pitchclass with a nearby 12edo pitch – without disrupting the pitch relationships and intervals as described in Parts I, II, and III.

In a broader sense, this option falls under the umbrella of adaptive just intonation (JI).

Use Case 2: Pedal steel guitar

Fig.3: Starter model of a Pedal Steel Guitar in E9 tuning
(audience view)

In Use Case 2 we take up the idea of non-tempered intervals over an equally tempered tonic. The E9 pedal steel guitar is a console instrument with typically 10 strings (Fig.3), three foot pedals and four knee levers.

Instead of physical frets, the fretboard has fret marks that help the player to reproduce 12edo tonics (related to the open string), while the intervals between the strings are mostly tuned differently (i.e. just intervals, meantone, various best-practice tunings). In this way the instrument has a kind of built-in capability for adaptive just intonation.

Robert P. “Bob” Lee was a long-time promoter of the instrument. In his Thoughts about tuning he explained:

“Electronic tuners didn’t exist in the 60s. Everyone tuned by ear. The better your ear, the more in tune you were. Before I got an electronic tuner in the mid-70s, I tuned by ear using harmonics. That is what we refer to as “just intonation” (JI). Tuning everything to the center mark on a tuner is “equal temperament” (ET). Most steel players use JI or something close to it, with the pedaled “A” note tuned to 440 Hz (cycles per second).”

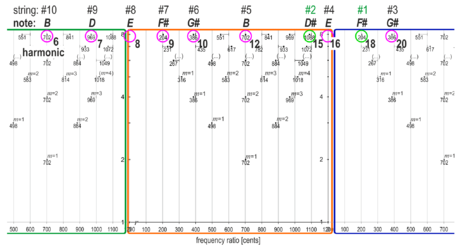
Fig.4 illustrates the basic tuning of the open strings (from low to high) forming a major E9 chord, shown here as intervals taken from an overtone scale. (Note that the #2 and #1 strings are out of order by design.)

Fig.4: Open strings of an E9 pedal steel guitar in overtone scale tuning

Fig.5: Steel bar

A steel guitar player holds a steel bar (Fig.5) in his left hand and presses it lightly against the strings (parallel to the fretmarks) as he moves it along the instrument’s neck, thus limiting the oscillating length of the strings.

As in Use Case 1, the tonic of course changes during the musical performance. However, the pedal steel guitar allows fine adjustment of the 12edo tonic, controlled by precise positioning of the steel bar and the player's ear. Thus, instead of only the tonic, any single ringing note can be aligned (or compromised) with 12edo when appropriate.

While playing the pedal steel guitar, the performer can change many of the open string intervals by up to two (tunable) half steps using pedals and knee levers. These changes can modify the actual tonic as well but the resulting complex possibilities are not taken into account in this analysis.

Listen to sparkling intervals and beatless chords in the following sound example:

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Video 1: Neck of a 10-string E9-pedal steel guitar:

The fret marks guide the player to 12edo intervals, while the intervals between the strings are often tuned differently (i.e. just intervals, meantone tuning, various best-practice tunings)

Use Case 3: The 7 Levels of Jazz Harmony

In August 2019 Adam Neely released his video The 7 Levels of Jazz Harmony

In section Level VII [09:12] he describes the use of a 12edo scale for the lead melody of a piece. The current melody note at any given point in time is treated as a reference pitch, and the current backing chord uses pure just intonation, while one note is perfectly in tune with the current 12edo reference pitch.

Level VII jazz harmony is an interesting example of applied adaptive just intonation, where neither the actual tonality (at any given point in time) nor anything like a harmonic context determines the pitch adaptation process of harmony notes.

In Use Case 1 and Use Case 2 a 12edo tuned tonic forms the base for adapted harmony notes and for melody notes as well. Use Case 3 uses a 12edo tuned melody note as the reference for adapted harmony notes. However, we notice that the intonation process is the same for all three use cases, only the reference pitch has changed from the "roots" (as quoted in Use Case 1) to a higher melody note in Use Case 3.

Fig.6: The first two bars of Level VII from Adam Neely’s The 7 levels of Jazz Harmony
with colored annotations

Fig.6 shows the first two bars of Adam Neely’s Level VII example. The orange annotations highlight the size of the intervals (related to the actual tonic) in (n+m)/n -notation with a common denominator n as found in AFDOs. The denominator n also represents the mode of an overtone scale. The +/- cents shown measure intonation relative to 12edo.

Planes in tonal space

In Part I of this series, we described the creation (expansion) of a 2D-plane in tonal space. We have explained that in this model all modes (n) of the overtone scale start at the same normalized pitch of 0 cents. The tonics of all of these overtone scales share exactly the same pitch – however, this pitch can be chosen arbitrarily. In analogy to a scale we could call the Horizon Chart from Part I a “relative concrete interval system”.

The desire for the integration of equally tempered pitches establishes a separate 2D-plane for each pitchclass of a 12edo scale – a scale that is obviously different from the overtone scale represented on the plane itself. Since we are creating these planes in a separate (third) dimension, we are free to apply any scale we like (with any number of scale steps).

The third dimension of tonal space is the dimension of the tonic ([math]\displaystyle{ u }[/math]). If we choose a 12edo scale in tonic direction for the distance between the planes we get the 3D representation of tonal space shown in Fig.7. The chosen scale determines the distances between the additional planes along the tonic ([math]\displaystyle{ u }[/math]) axis.

In this example the distance between the planes in tonic direction is 100 cents. Additionally the planes are shifted by 100 cents in r-direction, which points upward along the keyboard. There is a separate (r,n)-plane for each pitchclass, so we can name the planes by pitchclass identifiers like D, D#, E, F, ...A. Note, that it is useful to assign a tunable reference frequency (concert pitch, i.e. 440 Hz) to the tonic of plane A (marked in green).

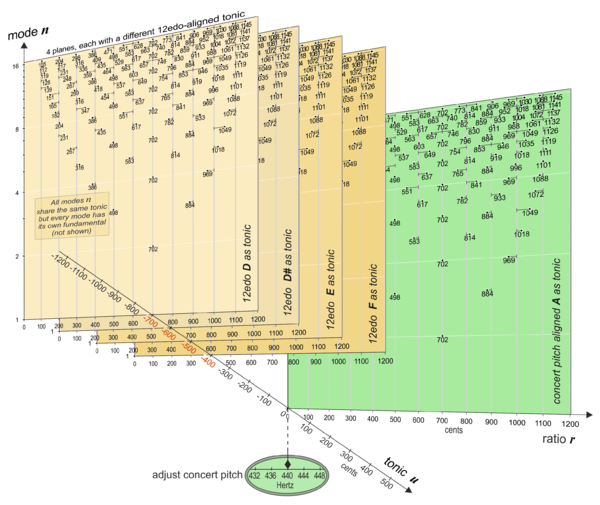
Fig.7: View of 3D-tonal space with a dimension of tonic

Adaptive just intonation (JI)

Up to this point, we have come across the term adaptive just intonation in several places. The term appears in the Use Cases 1-3 mentioned above. The Xenharmonic Wiki provides a definition for adaptive just intonation:

“Adaptive just intonation (adaptive JI) is an approach to just intonation that employs…

1. predefined musical intervals as frequency ratios over
2. a floating tonal center that is defined by
3. the most recent context.”

Ad 1.: The 3D-model of tonal space provides a set of predefined musical intervals on every plane associated with a pitchclass and between these planes.
Ad 2.: We rename floating tonal center to adapted tonic. Tonic adaptation is part of the model and is reflected by the selection of one active ([math]\displaystyle{ n,r }[/math])-plane at a given time.
Ad 3.: The phrase that a floating tonal center is defined by the most recent context is the least focused part of the definition. Our interpretation of this phrase is as follows:

The adaptation of the tonic can be influenced by the most recent harmonic context and should be controlled by the artistic intent of the composer or performer. There is no unambiguous solution for positioning the tonic.

A 12edo scale along the tonic axis

The proposed 3D-model includes a complete set of rational intervals for each 12edo-aligned tonic. With these 3D extensions, a novel instrument has access to a wide variety of pitches, allowing free modulation through twelve chromatic keys. No matter what interval we take from the model – every one of its pitches can be found aligned with 12edo as long as the corresponding harmonic index appears as a mode on the mode ([math]\displaystyle{ n }[/math]) axis. This means that the 3D model covers the intervals required for adaptive just intonation, as exemplified in Use Cases 1, 2, and 3.

Applying a non-12edo scale along the tonic axis

The scale intervals along the tonic ([math]\displaystyle{ u }[/math]) axis come into play whenever the tonic changes during the performance of a piece of music. If we choose a 12edo scale, the intervals of these tonic changes will be the same size regardless of the key in which the music is performed and regardless of any key changes in a composition.

However, there are examples of adaptive just intonation where the intervals for tonic changes are also taken from a just intonation scale.

Tonal space as an interval system

From the Tuning system page we learn that the visualized 3D-Model of tonal space with 12edo-spaced tonics (as shown in Fig.7) falls into the category of an interval system, also known as a tuning system.

The 3D-model of tonal space can be classified as a concrete tuning system:

“…A concrete tuning system defines exact intervals between all of its possible notes. Examples include untempered just intonation and equal tunings.”

In addition, the model is classified as an open system. (We have seen in Part II how the model can be extended in different directions.)

Coda

With the 3D model of tonal space, we have taken the first necessary step "toward building an electronic keyboard instrument that allows the player to interactively map sequences of rational intervals to consecutive keys - in real time, even live on stage".

The 3D interval system of the model forms a static framework that provides ”all the notes [pitches] or intervals theoretically available to a composer”. No floating tonic ("floating tonal center") appears for adaptive just intonation, possible target tonics are well defined and already part of the model.

When the total number of available pitches is added up, the model of tonal space can become quite large. The exact number of possible intervals depends on the highest implemented mode [math]\displaystyle{ n }[/math] of the overtone scale and the applied constraints necessary for the practical application in an instrument.

Of course, not all modeled pitches need to ring at the same time. Relationships between intervals are modeled in a well-structured way, allowing convenient retrieval of subgroups of related pitches and intervals.

Some questions were left unanswered in Parts I–IV of this series about the expansion of Tonal Space:

• How to retrieve groups of related intervals from the model?
• How to assign scales to a keyboard on the fly?
• How can the player of a novel instrument create chords of selected pitches from these scales?

There are good reasons to have more XenWiki pages that help to find answers to these questions...

See also...

The Pedal Steel Pages], a famous webresource that helps to answer many questions about the pedal steel guitar