Kite Guitar originals
The following songs have been composed for the Kite Guitar. To search for a certain song, artist or translator, use control-F in your browser. All tabs are for a guitar tuned in downmajor 3rds, unless otherwise noted. See Kite Guitar Chord Shapes (downmajor tuning) for reference on fingerings, inversions, etc.
Actual compositions are on separate xenwiki pages, grouped by composer. if you have any compositions, feel free to create your own page and link to it here! To keep this page current, please copy the table of contents from your page and paste it here (see this page for help).
By Kite Giedraitis
- 1 Evening Rondo
- 2 Underground Revolution
- 3 I Hear Numbers
- 4 Sweet Sweet Harmony (barbershop tag)
- 5 Downminor Etude
- 6 Blues in G
- 7 The Relative Song
- 8 The Tri-sub song
- 9 The Walking Song
- 10 II-V-I riff in A downmajor
- 11 Latrizo Pump riff
- 12 6-chord riff
- 13 V9 - I7 riff
- 14 Im7 - V7 riff
- 15 Fun riff
- 16 Mid-9th riff
- 17 James-Bond-ish riff
- 18 Downminor riff
By Praveen Venkataramana
How to read the scores
The octave is divided into 41 equal steps, a tuning called 41-ET or 41edo or 41-equal. Whereas 12-equal has 100¢ steps, 41-equal has steps of 29.27¢. We can round this off to 30¢ for convenience, since a cent or two doesn't matter much in practice. This 30¢ interval is called an arrow, because the little arrows by the noteheads raise or lower the pitch by 30¢. Notes are called up-E, down-F-sharp, etc., written ^E and vF#. A note that has no ups or downs is called plain. The 7 plain natural notes are close to 12-equal, but they do deviate slightly. The pattern is easy to see when the notes are arranged in chain-of-5ths order:
| Ab | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# |
| -15¢ | -12.5¢ | -10¢ | -7.5¢ | -5¢ | -2.5¢ | 0¢ | +2.5¢ | +5¢ | +7.5¢ | +10¢ | +12.5¢ | +15¢ |
All the notes with sharps are extra-sharp. All the notes with flats are extra-flat. Note that G# is sharper than Ab by one arrow. Thus G# is also ^Ab, and Ab is also vG#. (Likewise C# = ^Db, vD# = Eb, etc.) Since G# ≠ Ab, the familiar circle of 12 fifths opens up into a spiral. Because this spiral is really a circle of 41 fifths, the innermost and outermost few notes are duplicates.

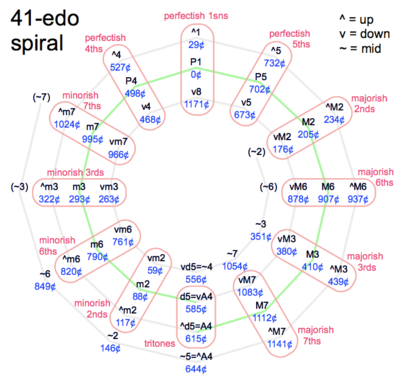
In the table, D is the "anchor note" that agrees with standard tuning exactly. D is an ideal anchor because it makes the table symmetrical. But F, C, G and A have all been used by microtonalists historically. If hired to record a part remotely, always ask what the anchor note is!
Assuming D is the anchor note, let's find some pitches. ^D is 30¢ sharp and vD is 30¢ flat. F# is +10¢, so vF# is -20¢. C is -5¢, so vC is -35¢. In certain situations, double arrows are needed. ^^C is called dup-C and vvC# is dud-C-sharp. Note that ^^C = vvC#. One more equivalence: ^^C = vDb. Thus 3 arrows = a minor 2nd. These equivalences are useful, because if you've already found vDb on your instrument, and you see ^^C on the score, you know what to do.
- one arrow = half a fret = a quarter-sharp or quarter-flat
- two arrows = one fret = half a sharp/flat
- three arrows = 1.5 frets = a minor 2nd
- four arrows = two frets = one sharp/flat = an augmented unison
This table lists all the notes, with equivalent names. It also lists intervals. Mid intervals, written with "~", are midway between major and minor.
| 41-equal note | tuning | interval from D | |
|---|---|---|---|
| D | D | +0¢ | P1 |
| ^D | D | +29¢ | ^1 |
| ^^D / vvD# / vEb | Eb | -41¢ | ^^1 / vvA1 / vm2 |
| vD# / Eb | Eb | -12¢ | vA1 / m2 |
| D# / ^Eb | Eb | +17¢ | A1 / ^m2 |
| ^D# / ^^Eb / vvE | Eb | +46¢ | ^A1 / ~2 |
| vE | E | -24¢ | vM2 |
| E | E | +5¢ | M2 |
| ^E / vvF | E | +34¢ | ^M2 |
| ^^E / vF | F | -37¢ | vm3 |
| F | F | -7¢ | m3 |
| ^F | F | +22¢ | ^m3 |
| ^^F / vvF# / vGb | F# | -49¢ | ~3 |
| vF# / Gb | F# | -20¢ | vM3 |
| #F / ^Gb | F# | +10¢ | M3 |
| ^F# / ^^Gb / vvG | F# | +39¢ | ^M3 |
| vG | G | -32¢ | v4 |
| G | G | -2¢ | P4 |
| ^G | G | +27¢ | ^4 |
| ^^G / vvG# / vAb | G# | -44¢ | ~4 / vd5 |
| vG# / Ab | G# | -15¢ | vA4 / d5 |
| #G / ^Ab | G# | +15¢ | A4 / ^d5 |
| ^G# / ^^Ab / vvA | G# | +44¢ | ^A4 / ~5 |
| vA | A | -27¢ | v5 |
| A | A | +2¢ | P5 |
| ^A | A | +32¢ | ^5 |
| ^^A / vvA# / vBb | Bb | -39¢ | ^^5 / vvA5 / vm6 |
| vA# / Bb | Bb | -10¢ | vA5 / m6 |
| A# / ^Bb | Bb | +20¢ | A5 / ^m6 |
| ^A# / ^^Bb / vvB | Bb | +49¢ | ^A5 / ~6 |
| vB | B | -22¢ | vM6 |
| B | B | +7¢ | M6 |
| ^B / vvC | B | +37¢ | ^M6 |
| ^^B / vC | C | -34¢ | vm7 |
| C | C | -5¢ | m7 |
| ^C | C | +24¢ | ^m7 |
| ^^C / vvC# / vDb | C# | -46¢ | ~7 |
| vC# / Db | C# | -17¢ | vM7 |
| #C / ^Db | C# | +12¢ | M7 |
| ^C# / ^^Db / vvD | C# | +41¢ | ^M7 |
| vD | D | -29¢ | v8 |
| D | D | +0¢ | P8 |
So how exactly would a vocalist or violinist or trombonist tune a precise number of cents sharp or flat? It helps to borrow a Kite guitar and familiarize oneself with the sound of the various intervals. It also helps to understand just intonation. See the "What it is -- long explanation" page for an overview. In practice, use the ups and downs as a rough guide, then listen to the other parts and try to blend. For example, the downmajor 3rd from D to vF# is 380¢, very close to the just 5/4 of 386¢. So one simply flattens the F# until the interference beats go away. But wait, should the 3rd be 380¢ or 386¢? In general, deviating slightly from 41-equal is fine, if it makes the chord smoother. The just harmonic 7th is only 3¢ sharp of the 41-equal downminor 7th, so such deviation is even less of an issue.
Of course, not all composers use simple JI ratios in their harmonies!
See also: Ups and downs notation
How to read the chord names
Any chord name without ups or downs is exactly what one would expect it to be. Cm7 is still C Eb G Bb. But in practice most chords have ups and downs in them. An up or down between the chord root and the chord type (e.g. C^m7) raises or lowers the 3rd, and also the 6th, 7th or 11th, if present. Thus C down-seven is the usual C7 chord with the 3rd and 7th downed: Cv7 = C vE G vBb. Mnemonic: every other note of a stacked-3rds chord with a 6th below the root is affected: 6th - root - 3rd - 5th - 7th - 9th - 11th - 13th. Note that the 6th is affected, but the 13th is not.
If the 3rd is downed but the minor 7th is not, the chord is named C-down add7, written Cv,7. The comma before the 7 means "add". Analogous to M and m, "a" means augmented and "d" means diminished. Half-diminished chords are named as dim add7 chords. For example, C ^Eb Gb ^Bb is C^d^7.
Alterations are enclosed in parentheses, additions never are. For example Cv(vv#5) is C vE vvG#.
See also: