User:Holger Stoltenberg/sandbox
Expanding tonal space
This article describes how to visually arrange a set of overtone scales in order to expand a particular plane of tonal space.
Why expand tonal space in this way?
The concept is a step towards building an electronic keyboard instrument that allows the player to interactively map sequences of rational intervals to consecutive keys – in real time, even live on stage. Therefore, the player needs convenient and intuitive access to the mapping process, which becomes an integral part of the musical performance.
With a prototypical instrument in place, the search for intermediary chords in tonal music begins. We can identify (and play) supplementary consonant chords that fit seamlessly into the gaps of familiar chord progressions. Listen to the following two audio examples to get the idea...
| Listen to | Control | Info |
|---|---|---|
| ...a sequence of five beatless minor chords |
[math]\displaystyle{ I }[/math]min, [math]\displaystyle{ I }[/math]min, [math]\displaystyle{ IV }[/math]min, [math]\displaystyle{ IV }[/math]min, [math]\displaystyle{ I }[/math]min | |
| ...an inserted intermediary chord on the 2nd beat |
[math]\displaystyle{ I }[/math]min, [math]\displaystyle{ I }[/math]xen-augmin, [math]\displaystyle{ IV }[/math]min, [math]\displaystyle{ IV }[/math]min, [math]\displaystyle{ I }[/math]min ... |
The proposed model of tonal space utilizes the uniform structure and simple mathematical description of overtone scales as well as the closely related arithmetic frequency division of the octave (AFDO).
For each note to be rendered, the model should effectively determine the current deviation from 12-tone equal temperament (12edo) in order to control the intonation of a commercial sound module or software plug-in on the fly.
How to expand tonal space – the interval axis
Like frequency, musical pitch is one-dimensional. Fig.1 illustrates the horizontal axis of tonal space, which we call the interval axis. It points in keyboard direction from low keys to high keys. The first harmonic (h1) is known as the common fundamental of all upcoming overtone scales.

- Fig.1: One octave (from the first harmonic h1 to the second harmonic h2)
The mode axis
The vertical axis of our model of tonal space indicates modes of the harmonic series. All modes start at the same normalized frequency (or pitch) of 0 cents. This means that the tonics of all of these overtone scales share exactly the same pitch (Fig. 2), which can be chosen arbitrarily.
Since each mode (row) begins with a member of the harmonic series, we can space adjacent modes by corresponding rational intervals for plotting on the logarithmic vertical axis.
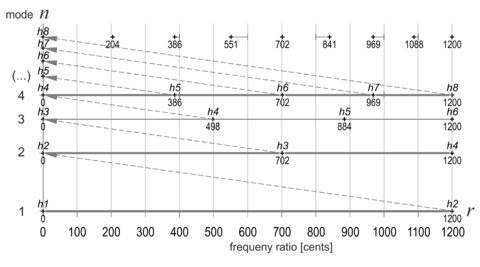
- Fig. 2: Overtone scales from Mode 1 (h1) to Mode 4 (h4) on a 2D-plane of tonal space
The Horizon Chart
The result of visualizing more modes of the overtone scale (up to Mode 16) is shown in Fig. 3:
- Fig. 3: The Horizon Chart: Relations of overtone scales (up to Mode 16) on a plane of tonal space
Each pitch is labeled with the size of an interval in cents, measured from the tonic (0 ¢) to the corresponding pitch marker (+). Each pitch marker is connected to the next vertical 12edo-line by a delta indicator. We define the direction and length of this indicator as the signed intonation interval of the respective pitch.
The AFDO-page can help to reproduce this plot:
- Within each period of any n-afdo system, the frequency ratio r of the m-th degree is
- [math]\displaystyle{ \displaystyle r=\frac{n+m}{n} }[/math] , where
- r is a rational frequency ratio which – after conversion to cents –
is displayed against the horizontal interval axis of tonal space - n is the mode of an overtone scale, plotted on the vertical axis
- m addresses (indexes, counts) the elements of each overtone scale in horizontal direction from the tonic (left, starting at 0) to the right.
- r is a rational frequency ratio which – after conversion to cents –
In particular ...
- if m = 0, then r = 1 (0 ¢) and
- if m = n, then r = 2 (1200 ¢)
An Example: A just major third relates the first (m=1) interval of a Mode 4 overtone scale to the tonic of Mode 4 (n=4, m=0) and we get
- [math]\displaystyle{ r=\frac{4+1}{4}=\frac{5}{4} }[/math]
- [math]\displaystyle{ r_{cents}= ln(r)\cdot\frac{1200}{ln(2)} \approx 386 }[/math] ¢
Intonation
Intonation is an adjustment of pitch applied to notes - live at performance time.
In the context of this model, we use 12edo pitches as the reference scale for measuring intonation. To describe intonation precisely (and without reference to concert pitch or absolute frequency), we define
- Intonation is the signed interval between...
- a pitch, generated by a key with a given key descriptor (such as A3, B3, C4, C#4, ...),
that rings exactly in tune with 12-tone equal temperament (12edo) and - a deviating pitch referenced by the same key descriptor
- a pitch, generated by a key with a given key descriptor (such as A3, B3, C4, C#4, ...),
- Intonation is the signed interval between...
Typically, intonation is a small interval between -50 ¢ and +50 ¢ although larger values are allowed. The common tonic of all modes of the overtone scale has an intonation of 0 ¢ by definition.
According to this definition, the upper pitch of the just major third (Mode 4) above the tonic has a signed intonation interval (distance to the next vertical 12edo line) of -14 ¢ .
To calculate the intonation
- compute the remainder of the interval’s value in cents by a modulo division (386 ¢ mod100) –
the intermediate result is 86 ¢ - Test: If the intermediate result is greater than 50 ¢ then subtract 100 ¢
- The test is true and the final result is -14 ¢
To determine the 12edo interval the intonation is applied to, get the original interval rcents and do some more integer arithmetic:
- [math]\displaystyle{ r_{12edo}=integer\left (\frac{r_{cents}+50c}{100.0} \right )\cdot 100 }[/math]
- [math]\displaystyle{ r_{12edo}=integer\left (\frac{386c+50c}{100.0} \right )\cdot 100=400 }[/math] ¢
A variety of projections of the model
Keep in mind that Fig.3 is just one graphical representation of relationships between pitches, musical intervals and overtone scales. More specifically, Fig.3 shows one of many useful Cartesian projections of an abstract model onto a 2D-plane. This kind of Cartesian projection of tonal space (with a straight horizontal line for each mode of an overtone scale) can be easily handled in a programming environment.