Temperament addition
(THIS PAGE IS A WIP)
Temperament arithmetic is the general name for either the temperament sum or the temperament difference, which are two closely related operations on regular temperaments. Basically, to do temperament arithmetic means to match up the entries of temperament vectors and then add or subtract them individually. The result is a new temperament that has similar properties to the original temperaments.
For example, the sum of 12-ET and 7-ET is 19-ET because ⟨12 19 28] + ⟨7 11 16] = ⟨(12+7) (19+11) (28+16)] = ⟨19 30 44], and the difference of 12-ET and 7-ET is 5-ET because ⟨12 19 28] - ⟨7 11 16] = ⟨(12-7) (8-11) (12-16)] = ⟨5 8 12]. We can write these using wart notation as 12p + 7p = 19p and 12p - 7p = 5p, respectively. The similarity in these temperaments can be seen in how, like both 12-ET and 7-ET, 19-ET (their sum) and 5-ET (their difference) both also support meantone temperament.
Temperament sums and differences can also be found using commas; for example meantone + porcupine = tetracot because [4 -4 1⟩ + [1 -5 3⟩ = [(4+1) (-4+-5) (1+3)⟩ = [5 -9 4⟩ and meantone - porcupine = dicot because [4 -4 1⟩ - [1 -5 3⟩ = [(4-1) (-4--5) (1-3)⟩ = [3 1 -2⟩. We could write this in ratio form — replacing addition with multiplication and subtraction with division — as 80/81 × 250/243 = 20000/19683 and 80/81 ÷ 250/243 = 25/24, respectively. The similarity in these temperaments can be seen in how all of them are supported by 7-ET.
Temperament arithmetic is simplest for temperaments which can be represented by single vectors such as demonstrated in these examples. In other words, it is simplest for temperaments that are either rank-1 (equal temperaments, or ETs for short) or nullity-1 (having only a single comma). Because grade [math]\displaystyle{ g }[/math] is the generic term for rank [math]\displaystyle{ r }[/math] and nullity [math]\displaystyle{ n }[/math], we could define the minimum grade [math]\displaystyle{ \min(g) }[/math] of a temperament as the minimum of its rank and nullity [math]\displaystyle{ \min(r,n) }[/math], and so for convenience in this article we will refer to [math]\displaystyle{ r=1 }[/math] (read "rank-1") or [math]\displaystyle{ n=1 }[/math] (read "nullity-1") temperaments as [math]\displaystyle{ \min(g)=1 }[/math] (read "min-grade-1") temperaments.
For [math]\displaystyle{ \min{g}\gt 1 }[/math] temperaments, temperament arithmetic gets a little trickier. This is discussed in the beyond min-grade-1 section later.
Visualizing temperament arithmetic
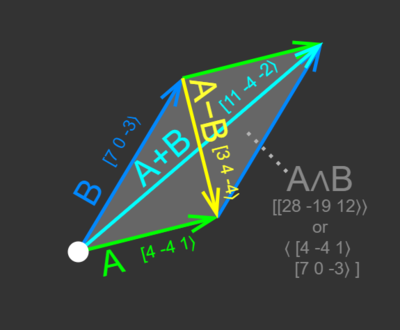
Versus the wedge product
If the wedge product of two vectors represents the directed area of a parallelogram constructed with the vectors as its sides, then the temperament sum and difference are the vectors that connect the diagonals of this parallelogram.
Tuning and tone space
One way we can visualize temperament arithmetic is on projective tuning space.

This shows both the sum and the difference of porcupine and meantone. All four temperaments — the two input temperaments, porcupine and meantone, as well as the sum, tetracot, and the diff, dicot — can be seen to intersect at 7-ET. This is because all four temperaments' mappings can be expressed with the map for 7-ET as one of their mapping rows.
These are all [math]\displaystyle{ r=2 }[/math] temperaments, so their mappings each have one other row besides the one reserved for 7-ET. Any line that we draw across these four temperament lines will strike four ETs whose maps have a sum and difference relationship. On this diagram, two such lines have been drawn. The first one runs through 5-ET, 20-ET, 15-ET, and 10-ET. We can see that 5 + 15 = 20, which corresponds to the fact that 20-ET is the ET on the line for tetracot, which is the sum of porcupine and meantone, while 5-ET and 15-ET are the ETs on their lines. Similarly, we can see that 15 - 5 = 10, which corresponds to the fact that 10-ET is the ET on the line for dicot, which is the difference of porcupine and meantone.
The other line runs through the ETs 12, 41, 29, and 17, and we can see again that 12 + 29 = 41 and 29 - 12 = 17.

We can also visualize temperament arithmetic on projective tone space. Here relationships are inverted: points are lines, and lines are points. So all four temperaments are found along the line for 7-ET.
Note that when viewed in tuning space, the sum is found between the two input temperaments, and the difference is found on the outside of them, to one side or the other. While in tone space, it's the difference that's found between the two input temperaments, and its the sum that's found outside. In either situation when a temperament is on the outside and may be on one side or the other, the explanation for this can be inferred from behavior of the scale tree on any temperament line, where e.g. if 5-ET and 7-ET support a [math]\displaystyle{ r=2 }[/math] temperament, then so will 5 + 7 = 12-ET, and then so will 5 + 12 and 7 + 12 in turn, and so on and so on recursively; when you navigate like this, what we could call down the scale tree, children are always found between their parents. But when you try to go back up the scale tree, to one or the other parent, you may not immediately know which side of the child to go.
Conditions on temperament arithmetic
Temperament arithmetic is only possible for temperaments with the same dimensions, that is, the same rank and dimensionality (and therefore, by the rank-nullity theorem, also the same nullity). The reason for this is visually obvious: without the same [math]\displaystyle{ d }[/math], [math]\displaystyle{ r }[/math], and [math]\displaystyle{ n }[/math] (dimensionality, rank, and nullity, respectively), the numeric representations of the temperament — such as matrices and multivectors — will not have the same proportions, and therefore their entries will be unable to be matched up one-to-one. From this condition it also follows that the result of temperament arithmetic will be a new temperament with the same [math]\displaystyle{ d }[/math], [math]\displaystyle{ r }[/math], and [math]\displaystyle{ n }[/math] as the input temperaments.
Matching the dimensions is only the first of two conditions on the possibility of temperament arithmetic. The second condition is that the temperaments must all be addable. This condition is trickier, though, and so a detailed discussion of it will be deferred to a later section (here: Temperament arithmetic#Addability). But we can at least say here that any set of min-grade-1 temperaments are addable[1], fortunately, so we don't need to worry about it in that case.
Versus meet and join
Like meet and join, temperament arithmetic takes temperaments as inputs and finds a new temperament sharing properties of the inputs. And they both can be understood as, in some sense, adding these input temperaments together.
But there is a big difference between temperament arithmetic and meet/join. Temperament arithmetic is done using entry-wise addition (or subtraction), whereas meet/join are done using concatenation. So the temperament sum of mappings with two rows each is a new mapping that still has exactly two rows, while the other hand, the join of mappings with two rows each is a new mapping that has a total of four rows[2].
The linear dependence connection
Another connection between temperament arithmetic and meet/join is that they may involve checks for linear dependence.
Temperament arithmetic, as stated earlier, always requires addability, which is a more complex property involving linear dependence.
Meet and join does not necessarily involve linear dependence. Linear dependence only matters for meet and join when you attempt to do it using exterior algebra, that is, by using the wedge product, rather than the linear algebra approach, which is just to concatenate the vectors as a matrix and reduce. For more information on this, see Douglas Blumeyer and Dave Keenan's Intro to exterior algebra for RTT#The linearly dependent exception to the wedge product.
Beyond min-grade-1
As stated above, temperament arithmetic is simplest for temperaments which can be represented by single vectors, or in other words, temperaments that are [math]\displaystyle{ \min(g)=1 }[/math], and for other temperaments, the computation gets a little trickier. Here we'll look at how to handle it.
Multivector approach
The simplest approach is to use multivectors. This is discussed in more detail here: Douglas Blumeyer and Dave Keenan's Intro to exterior algebra for RTT#Temperament arithmetic.
Matrix approach
Temperament arithmetic for temperaments with both [math]\displaystyle{ r\gt 1 }[/math] and [math]\displaystyle{ n\gt 1 }[/math] can also be done using matrices, but it's significantly more involved than it is with multivectors. It works in essentially the same way — entry-wise addition or subtraction — but for matrices, it is necessary to make explicit the basis for the linearly dependent vectors shared between the involved matrices before performing the arithmetic. In other words, any vectors that can be found through linear combinations of any of the involved matrices' basis vectors must appear explicitly and in the same position of each matrix before the sum or difference is taken. But it is not as simple as determining the basis for these linearly dependent vectors and pasting them over the vectors as you found them, because the results may then be enfactored. And defactoring them without compromising the explicit linearly dependent basis vectors cannot be done using existing defactoring algorithms; it's a tricky process, or at least computationally intensive.
(Examples WIP)
Addability
Verbal explanation
In order to understand addability, we must work up to it, understanding these concepts in this order:
- linear dependence
- linear dependence between temperaments
- linear independence between temperaments
- linear independence between temperaments by only one basis vector (that's addability)
1. Linear dependence
This is explained here: linear dependence.
2. Linear dependence between temperaments
Linear dependence has been defined for the matrices and multivectors that represent temperaments, but it can also be defined for temperaments themselves. The conditions of temperament arithmetic motivate a definition of linear dependence for temperaments whereby temperaments are considered linearly dependent if either of their mappings or their comma bases are linearly dependent[3].
For example, 5-limit 5-ET and 5-limit 7-ET, represented by the mappings [⟨5 8 12]⟩ and [⟨7 11 16]⟩ may at first seem to be linearly independent, because the basis vectors visible in their mappings are clearly linearly independent (when comparing two vectors, the only way they could be linearly dependent is if they are multiples of each other, as discussed here). And indeed their mappings are linearly independent. But these two temperaments are linearly dependent, because if we consider their corresponding comma bases, we will find that they share the basis vector of the meantone comma [4 -4 1⟩.
To make this point visually, we could say that two temperaments are linearly dependent if they intersect in one or the other of tone space and tuning space. So you have to check both views.[4]
3. Linear independence between temperaments
Linear dependence may be considered as a boolean (yes/no, linearly dependent/independent) or it may be considered as an integer count of linearly dependent basis vectors (e.g. 5-ET and 7-ET, per the example in the previous section, are linear-dependence-1 temperaments).
It does not make sense to speak of the linear dependence between temperaments in this integer count sense. Here's an example that illustrates why. Consider two different [math]\displaystyle{ d=5 }[/math], [math]\displaystyle{ r=2 }[/math] temperaments. Both their mappings and comma bases are linearly dependent, but their mappings have linear-dependence of 1, while their comma bases have linear-dependence of 2. So what could the linear-dependence of this temperament be? We could, of course, define "min-linear-dependence" and "max-linear-dependence", as we defined "min-grade" (and could define "max-grade" [math]\displaystyle{ \max(g) }[/math]), but this does not turn out to be helpful.
However, it turns out that it does make sense to speak of the linear-independence of the temperament as an integer count. This is because the count of linearly independent basis vectors of two temperaments' mappings and the count of linearly independent basis vectors of their comma bases will always be the same. So the temperament linear-independence is simply this number. In the [math]\displaystyle{ d=5 }[/math], [math]\displaystyle{ r=2 }[/math] example from the previous paragraph, these would be linear-independence-1, or [math]\displaystyle{ l=1 }[/math] temperaments.
A proof of this is given here.
4. Linear independence between temperaments by only one basis vector (addability)
Two temperaments are addable if they are [math]\displaystyle{ l=1 }[/math]. In other words, both their mappings and their comma bases share all but one basis vector.
Diagrammatic explanation
How to read the diagrams
The diagrams used for this explanation were inspired in part by Kite's gencoms, and specifically how in his "twin squares" matrices — which have dimensions [math]\displaystyle{ d×d }[/math] — one can imagine shifting a bar up and down to change the boundary between vectors that form a basis for the commas and those that form a basis for preimage intervals (this basis is typically called "the generators"). The count of the former is the nullity [math]\displaystyle{ n }[/math], and the count of the latter is the rank [math]\displaystyle{ r }[/math], and the shifting of the boundary bar between them with the total [math]\displaystyle{ d }[/math] rows corresponds to the insight of the rank-nullity theorem, which states that [math]\displaystyle{ r }[/math] + [math]\displaystyle{ n }[/math] = [math]\displaystyle{ d }[/math]. And so this diagram's square grid has just the right amount of room to portray both the mapping and the comma basis for a given temperament (with the comma basis's vectors rotated 90 degrees to appear as rows, to match up with the rows of the mapping).
So consider this first example of such a diagram:
This represents a [math]\displaystyle{ d=4 }[/math] temperament. These diagrams are grade-agnostic, which is to say that they are agnostic as to which side counts the [math]\displaystyle{ r }[/math] and which side counts the [math]\displaystyle{ n }[/math]. Initially, though, it is probably simpler to explain things by arbitrary assigning each side of the line or the other of the two grades. So let's just say that the count of rows above the line is [math]\displaystyle{ r }[/math] and the count below the line is [math]\displaystyle{ n }[/math], so we can then say that this diagram represents a [math]\displaystyle{ r=1 }[/math], [math]\displaystyle{ n=3 }[/math] temperament.
Actually, this diagram represents more than just a single temperament. It represents a relationship between a pair of temperaments (which, of course, must have the same dimensions). Green coloration indicates linearly dependent basis vectors between this pair of temperaments, and red coloration indicates linearly independent basis vectors between the same pair of temperaments.
So, in this case, the two ET maps are linearly independent. This should be unsurprising; because ET maps are constituted by only a single vector (they're [math]\displaystyle{ r=1 }[/math] by definition), if they were linearly dependent, then they'd necessarily be the same exact ET! Temperament arithmetic on two of the same ET is never interesting; A plus A simply equals A again, and A minus A is undefined. That said, if we were to represent temperament arithmetic between two of the same temperament on such a diagram as this, then every cell would be green. And this is true regardless whether [math]\displaystyle{ r=1 }[/math] or otherwise.
From this information, we can see that the comma bases of any randomly selected pair of different [math]\displaystyle{ d=4 }[/math] ETs are going to share 2 vectors, or in other words, their linear dependence basis will have two basis vectors. In terms of the diagram, we're saying that they'll always have two green-colored rows under the black bar.
These diagrams are a good way to understand which temperament relationships are possible and which aren't, where by a "relationship" here we mean a particular combination of their shared dimensions and their linear-independence integer count. A good way to use these diagrams for this purpose is to imagine the red coloration emanating away from the black bar in both directions simultaneously, one pair of rows at a time. Doing it like this captures the fact, as previously stated, that the linear-independence (in the integer count sense) on either side of duality is always equal. There's no notion of a max or min here, as there is with grade or the linear-dependence (again, in the integer count sense); the linear-independence on either side is always the same, so we can capture it with a single number, which counts the red rows on just one half (that is, half of the total count of red rows, or half of the width of the red band in the middle of the grid).
There's no need to look at diagrams like this where the black bar is below the center. This is because, even though for convenience we're currently treating the top half as [math]\displaystyle{ r }[/math] and the bottom half as [math]\displaystyle{ n }[/math], these diagrams are ultimately grade-agnostic. So we could say that each one essentially represents not just one possibility for the relationship between two temperaments' dimensions and linear dependence, but two such possibilities. For example, this diagram equally represents both [math]\displaystyle{ d=4, r=1, n=3, l=1 }[/math] as well as [math]\displaystyle{ d=4, r=3, n=1, l=1 }[/math]. Which is another way of saying we could vertically mirror it without changing it.
With the black bar always either in the top half or exactly in the center, we can see that the emanating red band will always either hit the top edge of the square grid first, or they will hit both the top and bottom edges of it simultaneously. So this is how these diagrams visually convey the fact that the linear-independence between two temperaments will always be less than or equal to their min-grade: because a situation where [math]\displaystyle{ \min(g)\gt l }[/math] would visually look like the red band spilling past the edges of the square grid.
We could also say that two temperaments are linearly dependent on each other when [math]\displaystyle{ l\lt \max(g) }[/math], that is, their linear-independence is less than their max-grade.
Perhaps more importantly, we can also see from these diagrams that any pair of [math]\displaystyle{ \min(g)=1 }[/math] temperaments will be addable. Because if they are [math]\displaystyle{ \min(g)=1 }[/math], then the furthest the red band can extend from the black bar is 1 row, and 1 mirrored set of red rows means [math]\displaystyle{ l=1 }[/math], and that's the definition of addability.
A simple [math]\displaystyle{ d=3 }[/math] example
Let's back-pedal to [math]\displaystyle{ d=3 }[/math] for a simple illustrative example.
This diagram shows us that any two [math]\displaystyle{ d=3 }[/math], [math]\displaystyle{ r=1 }[/math] temperaments (like 5-limit ETs) will be linearly dependent, i.e. their comma bases will share one vector. You may already know this intuitively if you are familiar with the 5-limit projective tuning space diagram from The Middle Path paper, which shows how we can draw a line through any two ETs and that line will represent a temperament, and the single comma that temperament tempers out is this shared vector. The diagram also tells us that any two 5-limit temperaments that temper out only a single comma will also be linearly dependent, for the opposite reason: their mappings will always share one vector.
And we can see that there are no other diagrams of interest for [math]\displaystyle{ d=3 }[/math], because there's no sense in looking at diagrams with no red band, but we can't extend the red band any further than 1 row on each side without going over the edge, and we can't lower the black bar any further without going below the center. So we're done. And our conclusion is that any pair of different [math]\displaystyle{ d=3 }[/math] temperaments that are nontrivial ([math]\displaystyle{ 0 \lt n \lt d = 3 }[/math] and [math]\displaystyle{ 0 \lt r \lt d = 3 }[/math]) will be addable.
Completing the suite of [math]\displaystyle{ d=4 }[/math] examples
Okay, back to [math]\displaystyle{ d=4 }[/math]. We've already looked at the [math]\displaystyle{ \min(g)=1 }[/math] possibility (which, for any [math]\displaystyle{ d }[/math], there will only ever be one of). So let's start looking at the possibilities where [math]\displaystyle{ \min(g)=2 }[/math], which in the case of [math]\displaystyle{ d=4 }[/math] leaves us only one pair of values for [math]\displaystyle{ r }[/math] and [math]\displaystyle{ n }[/math]: both being 2.
But even with [math]\displaystyle{ d }[/math], [math]\displaystyle{ r }[/math], and [math]\displaystyle{ n }[/math] fixed, we still have more than one possibility for [math]\displaystyle{ l }[/math]. The above diagram shows [math]\displaystyle{ l=1 }[/math]. The below diagram shows [math]\displaystyle{ l=2 }[/math].
In the former possibility, where [math]\displaystyle{ l=1 }[/math] (and therefore the temperaments are addable), we have a pair of different [math]\displaystyle{ d=4 }[/math], [math]\displaystyle{ r=2 }[/math] temperaments where we can find a single comma that both temperaments temper out, and — equivalently — we can find one ET that supports both temperaments.
In the latter possibility, where [math]\displaystyle{ l=2 }[/math], neither side of duality shares any vectors in common. And so we've encountered our first example that is not addable. In other words, if the red band ever extends more than 1 row away from the black line, temperament arithmetic is not possible. So [math]\displaystyle{ d=4 }[/math] is the first time we had enough room (half of [math]\displaystyle{ d }[/math]) to support that condition.
We have now exhausted the possibility space for [math]\displaystyle{ d=4 }[/math]. We can't extend either the red band or the black bar any further.
[math]\displaystyle{ d=5 }[/math] diagrams finally reveal important relationships
So how about we go to [math]\displaystyle{ d=5 }[/math] (such as the 11-limit). As usual, starting with [math]\displaystyle{ \min(g)=1 }[/math]:
Just as with the [math]\displaystyle{ l=1 }[/math] diagrams given for [math]\displaystyle{ d=3 }[/math] and [math]\displaystyle{ d=5 }[/math], we can see these are addable temperaments.
Now let's look at [math]\displaystyle{ d=5 }[/math] but with [math]\displaystyle{ \min(g)=2 }[/math]. This presents two possibilities. First, [math]\displaystyle{ l=1 }[/math]:
And second, [math]\displaystyle{ l=2 }[/math]:
Here's where things really get interesting. Because in both of these cases, the pairs of temperaments represented are linearly dependent on each other (i.e. either their mappings are linearly dependent, their comma bases are linearly dependent, or both). And so far, every possibility where temperaments have been linearly dependent, they have also been [math]\displaystyle{ l=1 }[/math], and therefore addable. But if you look at the second case here, we are [math]\displaystyle{ l=2 }[/math], but since [math]\displaystyle{ d=5 }[/math], the temperaments still manage to be linearly dependent. So this is the first example of a linearly dependent temperament pairing which is not addable.
Back to [math]\displaystyle{ d=2 }[/math], for a surprisingly tricky example
Beyond [math]\displaystyle{ d=5 }[/math], these diagrams get cumbersome to prepare, and cease to reveal further insights. But if we step back down to [math]\displaystyle{ d=2 }[/math], a place simpler than anywhere we've looked so far, we actually find another surprisingly tricky example, which is hopefully still illuminating.
So [math]\displaystyle{ d=2 }[/math] (such as the 3-limit) presents another case — similar to the [math]\displaystyle{ d=5 }[/math], [math]\displaystyle{ \min(g)=2 }[/math], [math]\displaystyle{ l=2 }[/math] case shared most recently above — where the properties "linearly dependent" and "addable" do not match each other. But while in the other case, we had a temperament pair that was linearly dependent yet not addable, in this [math]\displaystyle{ d=2 }[/math] (and therefore [math]\displaystyle{ \min(g)=1 }[/math], [math]\displaystyle{ l=1 }[/math]) case, it is the other way around: addable yet linearly independent!
Basically, in the case of [math]\displaystyle{ d=2 }[/math], [math]\displaystyle{ \max(g)=1 }[/math] (in non-trivial cases, i.e. not JI or the unison temperament), so any two different ETs or commas you pick are going to be linearly independent (because the only way they could be linearly dependent would be to be the same temperament). And yet we know we can still entry-wise add them to new vectors that are decomposable, because they're already vectors (decomposing means to express a multivector in the form of a list of monovectors, so decomposing a multivector that's already a monovector like this is tantamount to merely putting array braces around it.)
Conclusion
This explanation has hopefully helped get a grip on what addability AKA [math]\displaystyle{ l=1 }[/math] is like. But it still hasn't quite explained why [math]\displaystyle{ l=1 }[/math] is one and the same thing as addability. We will look at this in another section soon.
Geometric explanation
(WIP)
Algebraic explanation
(WIP)
Applications
The temperament that results from summing or diffing two temperaments, as stated above, has similar properties to the original two temperaments. According to some sources, these properties are discussed in terms of "Fokker groups" on this page: Fokker block.
Sintel's proof of the linear independence conjecture
If A and B are mappings from Z^n to Z^m, with n > m, A, B full rank (i'll use A and B as their rowspace equivalently):
dim(A + B) - m = dim(ker(A) + ker(B)) - (n-m)
>> dim(A)+dim(B)=dim(A+B)+dim(A∩B) => dim(A + B) = dim(A) + dim(B) - dim(A∩B)
dim(A) + dim(B) - dim(A∩B) - m = dim(ker(A) + ker(B)) - (n-m)
>> by duality of kernel, dim(ker(A) + ker(B)) = dim(ker(A ∩ B))
dim(A) + dim(B) - dim(A∩B) - m = dim(ker(A ∩ B)) - (n-m)
>> rank nullity: dim(ker(A ∩ B)) + dim(A ∩ B) = n
dim(A) + dim(B) - dim(A∩B) - m = n - dim(A ∩ B) - (n-m)
m + m - dim(A∩B) - m = n - dim(A ∩ B) - (n-m)
m + m - m = n - n + m
m = m
References
- ↑ or they are all the same temperament, in which case they share all the same basis vectors and could perhaps be said to be completely linearly dependent.
- ↑ At least, this mapping would have a total of four rows before it is reduced. After reduction, it may end up with only three (or two if you joined a temperament with itself for some reason).
- ↑ or — equivalently, in EA — either their multimaps or their multicommas are linearly dependent
- ↑ You may be wondering — what about two temperaments which are parallel in tone or tuning space, e.g. compton and blackwood in tuning space? Their comma bases are each [math]\displaystyle{ n=1 }[/math], and they meet to give a [math]\displaystyle{ n=2 }[/math] comma basis, which corresponds to a [math]\displaystyle{ r=1 }[/math] mapping, which means it should appear as an ET point on the PTS diagram. But how could that be? Well, here's their meet: ⟨[1 0 0⟩ [0 1 0⟩], and so that corresponding mapping is [⟨0 0 1]⟩. So it's some degenerate ET. I suppose we could say it's the point at infinity away from the center of the diagram.