OTC 7L 12s: Difference between revisions
Jump to navigation
Jump to search
m Text replacement - "Category:Tempered scales↵Category:Pages with mostly numerical content" to "Category:Tempered_scales Category:Pages with mostly numerical content" Tag: Reverted |
m Text replacement - "Category:Tempered_scales↵Category:Pages with mostly numerical content" to "Category:Tempered scales Category:Pages with mostly numerical content" Tag: Manual revert |
||
| Line 114: | Line 114: | ||
<ul><li>Noted as omnitetrachordal by Paul Erlich no later than 2002. See tuning-math list messages [http://robertinventor.com/tuning-math/s___4/msg_3675-3699.html#3685 3685] and [http://robertinventor.com/tuning-math/s__11/msg_10975-10999.html#10987 10987].</li></ul> | <ul><li>Noted as omnitetrachordal by Paul Erlich no later than 2002. See tuning-math list messages [http://robertinventor.com/tuning-math/s___4/msg_3675-3699.html#3685 3685] and [http://robertinventor.com/tuning-math/s__11/msg_10975-10999.html#10987 10987].</li></ul> | ||
[[Category:19-tone scales]] | [[Category:19-tone scales]] | ||
[[Category: | [[Category:Tempered scales]] | ||
[[Category:Pages with mostly numerical content]] | [[Category:Pages with mostly numerical content]] | ||
[[Category:MODMOS]] | [[Category:MODMOS]] | ||
[[Category:Omnitetrachordal]] | [[Category:Omnitetrachordal]] | ||
[[Category:Flattone]] | [[Category:Flattone]] | ||
Latest revision as of 03:09, 24 June 2025
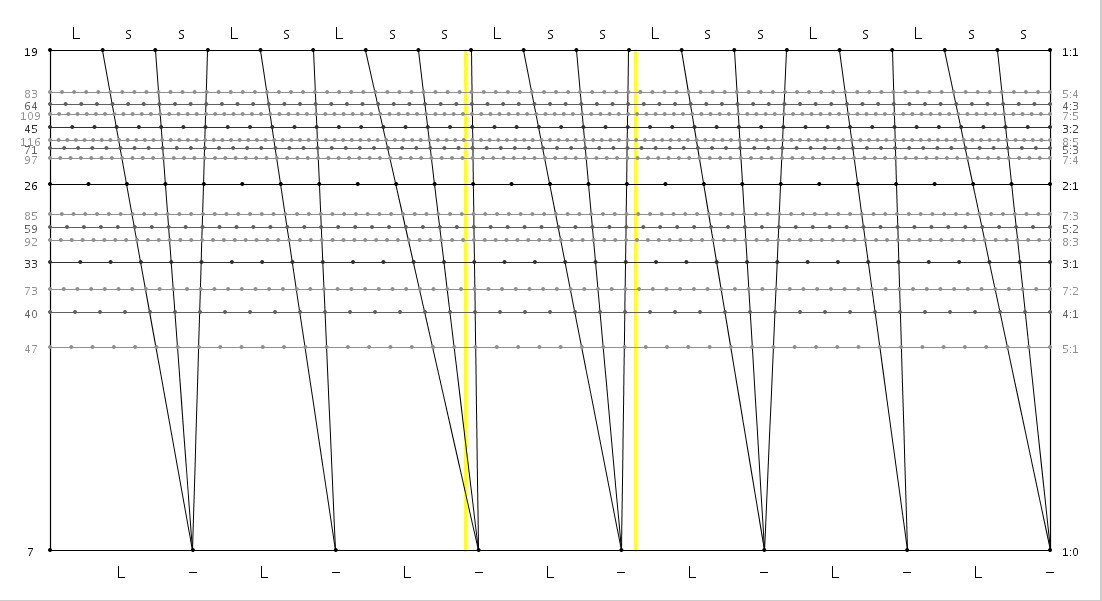
Omnitetrachordal MOS scale
19 tones (8+3+8)
Flattone MOS; P<0 (oddly, neither this scale nor its dual can be tuned with a perfect 3/2!)
P = -0.2063597584
Q = 5.0713810872 (4/3 = 3L+4.5s)
L = 63.16 to 171.43 cents (128.12 cents @ Q)
s = 0.00 to 63.16 cents (25.26 cents @ Q)
9/8 = L+2s (171.43 to 189.47 cents)
4/3 = 3L+5s (505.26 to 514.29 cents)
generator = 4/3
notable EDOs: 26, 33, 40, 45
symmetric mode: sLssLsLssLssLsLssLs
all modes:
| sLs sLsLssLs sLsLssLs | sLssLsLs sLssLsLs sLs | |
| Lss LsLssLss LsLssLss | LssLsLss LssLsLss Lss | |
| ssL sLssLssL sLssLssL | ssLsLssL ssLsLssL ssL | |
| sLs LssLssLs LssLssLs | sLsLssLs sLsLssLs sLs | |
| LsLssLss LsLssLss Lss | ||
| sLssLssL sLs sLssLssL | sLssLssL sLssLssL ssL | |
| LssLssLs Lss LssLssLs | LssLssLs LssLssLs sLs | |
| ssLssLsL ssL ssLssLsL | ||
| sLssLsLs sLs sLssLsLs | ||
| LssLsLss Lss LssLsLss | ||
| ssLsLssL ssL ssLsLssL | ||
| sLsLssLs sLs sLsLssLs | ||
| LsLssLss Lss LsLssLss | ||
| sLs sLssLssL sLssLssL | sLssLssL ssL sLssLssL | |
| Lss LssLssLs LssLssLs | LssLssLs sLs LssLssLs | |
| ssL ssLssLsL ssLssLsL | ||
| sLs sLssLsLs sLssLsLs | sLssLssL sLssLssL sLs | |
| Lss LssLsLss LssLsLss | LssLssLs LssLssLs Lss | |
| ssL ssLsLssL ssLsLssL | ssLssLsL ssLssLsL ssL |